Similar presentations:
Проводники в электростатическом поле
1. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
2. Напряженность и потенциал электростатического поля в проводнике
В проводниках имеются электрически заряженныечастицы – носители заряда (электроны в металлах, ионы в
электролитах) способные перемещаться по всему объему
проводника под действием внешнего электростатического
поля.
Носителями заряда в металлах являются электроны
проводимости. Они возникают при конденсации паров
металла за счет обобществления валентных электронов.
При отсутствии электрического поля металлический
проводник является электрически нейтральным –
электростатическое поле создаваемое положительными и
отрицательными зарядами внутри него компенсируется.
3.
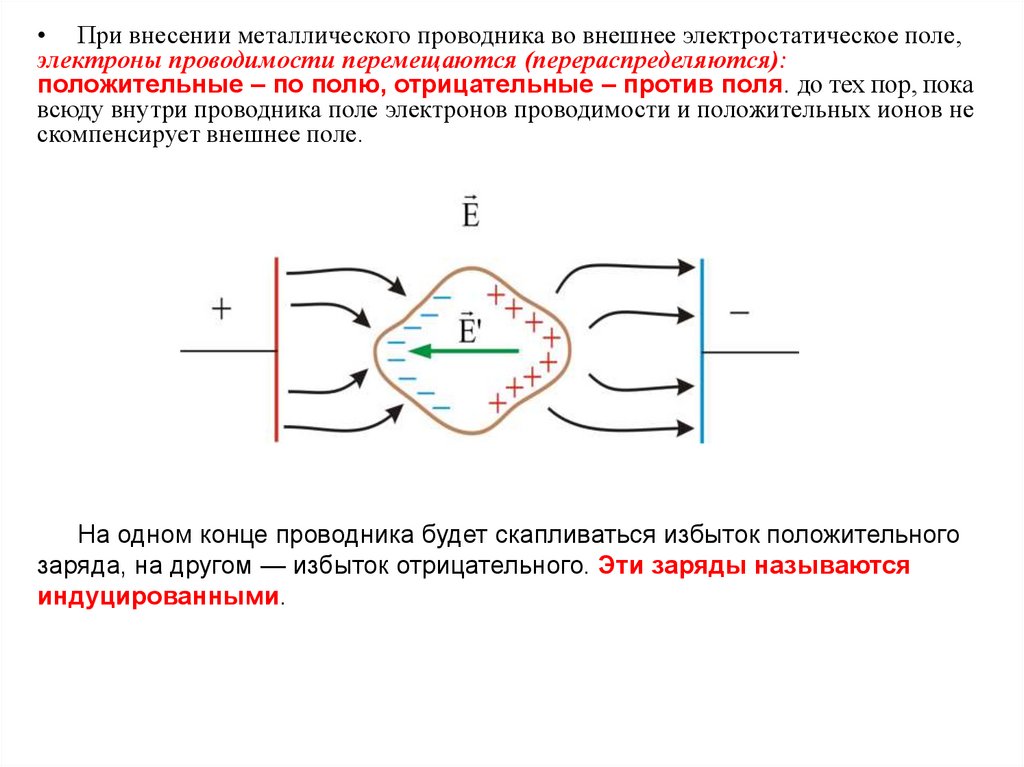
• При внесении металлического проводника во внешнее электростатическое поле,электроны проводимости перемещаются (перераспределяются):
положительные – по полю, отрицательные – против поля. до тех пор, пока
всюду внутри проводника поле электронов проводимости и положительных ионов не
скомпенсирует внешнее поле.
На одном конце проводника будет скапливаться избыток положительного
заряда, на другом — избыток отрицательного. Эти заряды называются
индуцированными.
4.
В установившимся состоянии в проводнике, помещенномв электростатическое поле мы имеем:
Появление у заряженной поверхности на металле заряда
противоположного знака – электростатическая индукция.
Этот процесс очень краток ~ 10–8 секунд.
•Электростатическое экранирование – внутрь проводника
поле не проникает.
•Во всех точках внутри проводника Е = 0, а во всех точках на
поверхности Е = En (Eτ = 0);
Весь объем проводника, находящегося в электростатическом
поле эквипотенциален.
ε ме .
•Диэлектрическая проницаемость
•На поверхности проводника напряженность
направлена по нормали
к этой поверхности, иначе, под действием составляющей Eτ, касательной к
поверхности, заряды перемещались бы по проводнику, а это противоречило
бы их статическому распределению.
5.
• Действительно, в любой точке внутри проводника,dφследовательно, φ = const.
dl
E 0
• Поверхность проводника тоже эквипотенциальна:
(для любой линии на поверхности)
dφ
• Потенциал
Eτ 0поверхности равен потенциалу объема
dl
проводника.
• В заряженном проводнике некомпенсированные
заряды, располагаются только на поверхности (их
расталкивают кулоновские силы).
Доказательство:
Согласно теореме Остроградского – Гаусса
q объема
DdS проводника
Eεε 0 dSравен
0,
суммарный заряд q внутри
нулю, так как Е=0
s
s
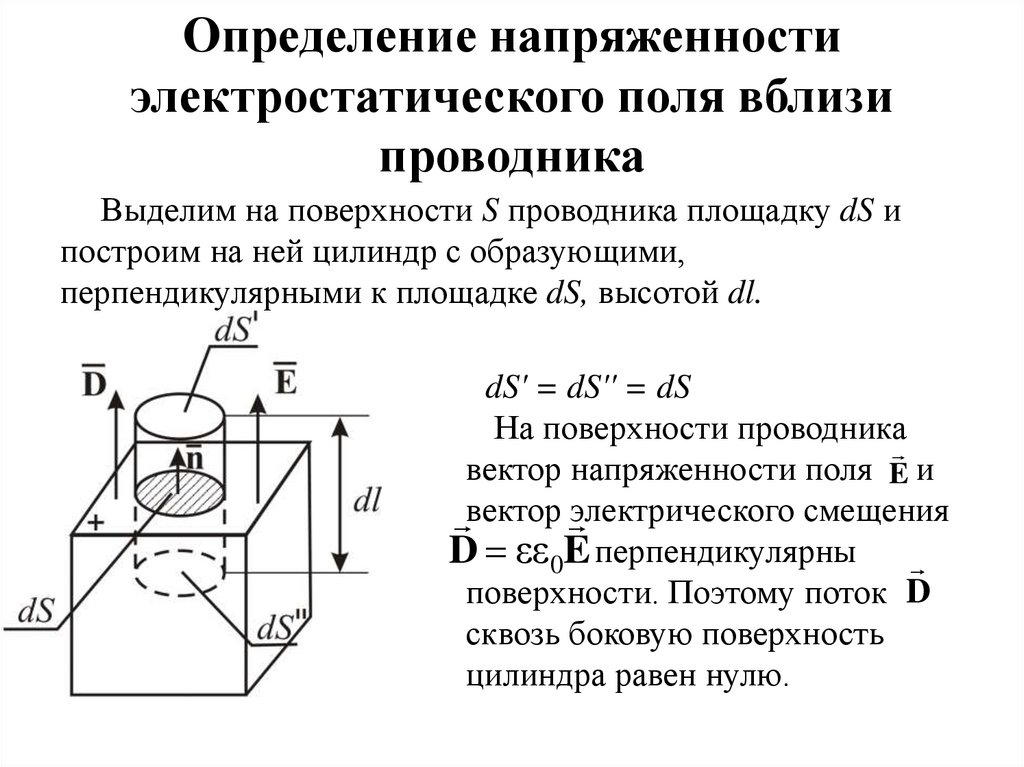
6. Определение напряженности электростатического поля вблизи проводника
Выделим на поверхности S проводника площадку dS ипостроим на ней цилиндр с образующими,
перпендикулярными к площадке dS, высотой dl.
dS' = dS'' = dS
На поверхности проводника
вектор напряженности поля E и
вектор электрического смещения
D εε0E перпендикулярны
поверхности. Поэтому поток D
сквозь боковую поверхность
цилиндра равен нулю.
7.
ФПоток вектора электрического смещения
через
dS'' тоже
D
равен нулю, так как dS''
и,
лежит внутри проводника, где
E 0
следовательно
D. 0
• Отсюда следует, что поток dФD сквозь замкнутую
поверхность равен потоку через
D dS':
dФD = DndS
С другой стороны по теореме Остроградского-Гаусса:
dФD = dq = σdS
где: σ – поверхностная плотность зарядов на dS. Из равенства
правых частей следует, что Dn = σ тогда
Dn
σ
(5.2.3)
En
ε 0ε
ε 0ε
Напряженность
поля
вблизи
поверхности
заряженного проводника прямо пропорцианальна
поверхностной плотности зарядов.
8.
• В состоянии равновесия внутри проводника зарядыотсутствуют, и создание внутри него полости не повлияет на
конфигурацию расположения зарядов и тем самым на
электростатическое поле.
• Если проводник с полостью заземлить, то потенциал во
всех точках полости будет нулевым, т. е. полость полностью
изолирована от влияния внешних электростатических полей.
•На этом основана электростатическая защита —
экранирование тел, например измерительных приборов, от
влияния внешних электростатических полей. Вместо
сплошного
проводника
для
защиты
может
быть
использована густая металлическая сетка.
•Свойство зарядов располагаться на внешней поверхности
проводника
используется
для
устройства
электростатических генераторов, предназначенных для
накопления больших зарядов и достижения разности
потенциалов в несколько миллионов вольт.
9. Конденсаторы Электрическая емкость.
При сообщении проводнику заряда, на егоповерхности появляется потенциал φ. Но если этот же
заряд сообщить другому проводнику, то потенциал будет
другой. Это зависит от геометрических параметров
проводника. Но в любом случае, потенциал φ
пропорционален заряду q.
q=Cφ
• Коэффициент
пропорциональности
называют
электроемкостью – физическая величина, численно
равна заряду, который необходимо сообщить проводнику
для того, чтобы изменить его потенциал на единицу.
10.
1 Кулон КлC
1 Фарад 1 Ф
1 Вольт
В
Один фарад – это емкость такого проводника, потенциал
которого изменяется на один вольт при сообщении ему
заряда в один кулон.
Найдем емкость уединенного проводящего шара (сферы):
1
q
E
2
4 0 r
Имеем:
при
1
Q
Edr
4 0 R
R
C 4 0 R
r R
q
C
Тогда:
- емкость проводящего шара (сферы).
11.
Электроемкость уединенного проводника зависит от егогеометрических размеров, формы и диэлектрических
свойств окружающей среды и не зависит от величины
заряда проводника.
Система проводников, емкость которой не зависит от
расположения
окружающих
тел,
называется
конденсатором, а сами проводники – обкладками
конденсатора.
Конденсаторы
Конденсатор служит для накопления заряда, он состоит
из
двух
обкладок,
разделенных
диэлектриком.
Конденсаторы разделяют на плоские, цилиндрические и
сферические.
12.
Так как поле сосредоточено внутри конденсатора, то линиинапряженности начинаются на одной обкладке и кончаются на
другой, поэтому свободные заряды, возникающие на разных
обкладках, являются равными по модулю разноименными
зарядами.
Под
емкостью
конденсатора
понимается
физическая величина, равная отношению заряда q ,
накопленного
в
конденсаторе,
к
разности
потенциалов между его обкладками:
13.
Плоский конденсаторПлоский конденсатор состоит из двух параллельных
пластин, площадью S каждая и находящихся на
расстоянии d.
+q
Напряженность внутри конденсатора:
-q
E
При (0 x d )
0
S
d
Тогда:
С другой стороны: E
d
d
dx
0
dx
Либо:
d
dx
0
Проинтегрируем левую и правую часть последнего выражения:
2
q
qd
d
d
d
x
2
1
S
0 S
0
0
0
1
14.
Из предыдущего слайда (путем замены знаков) имеем:qd
1 2
0 S
q
0 S
C
1 2
d
S
C 0
d
Тогда:
- емкость плоского
конденсатора.
Сферический конденсатор
Сферический конденсатор состоит из двух концентрических
металлических сфер, радиусов R1 и R2 (R1>R2).
Сфера создает электростатическое поле
-q
только вне этой сферы. При R>R2 поля
взаимно уничтожаются, а поле внутри
+q R1
создается только зарядом +q внутренней
R2
обкладки.
15.
1q
E
2
4 0 r
1
q
d
2
Er так как E grad
4 0 r
dr
q dr
d
Интегрируем:
4 0 r 2
q
q
1
q
dr
2 1
2
4 0 R1 r
4 0 r R1 4 0
R2
R2
4 0 R1 R2
4 0
q
C
R2 R1
1 2 1 1
R1 R2
1
1
R2 R1
4 0 R1 R2
С
R2 R1
Емкость сферического конденсатора
16.
Цилиндрический конденсатор+q
+q
-q
R2-R1=d – толщина
прослойки диэлектрика.
R1
R2
-q
L
Вид с торца
По т. Гауса-Остроградского:
r – текущий радиус
q
S E dS 0
q
S E dS E 2 r L 0
d E dr
L>>d, R1< r <R2
Интегрируем:
S 2 r L
q
E
2 rL 0
2 1 E dr
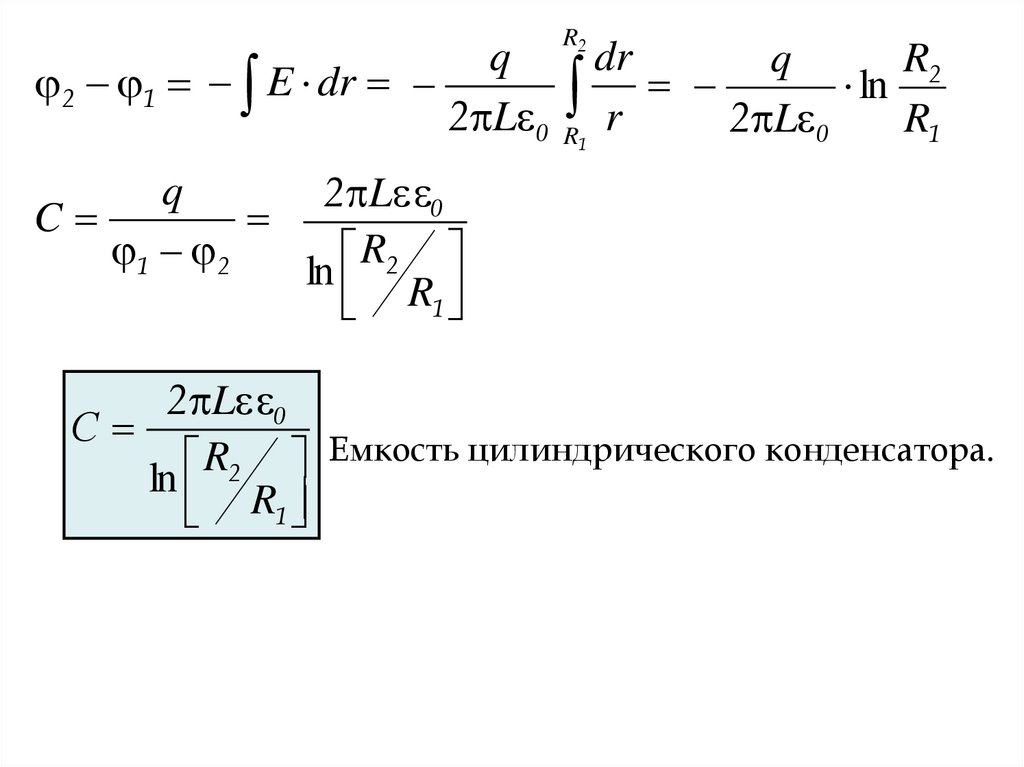
17.
q2 1 E dr
2 L 0
R2
dr
q
R2
R r 2 L 0 ln R1
1
q
2 L 0
C
R2
1 2
ln
R1
2 L 0
С
R2 Емкость цилиндрического конденсатора.
ln
R1
18.
19.
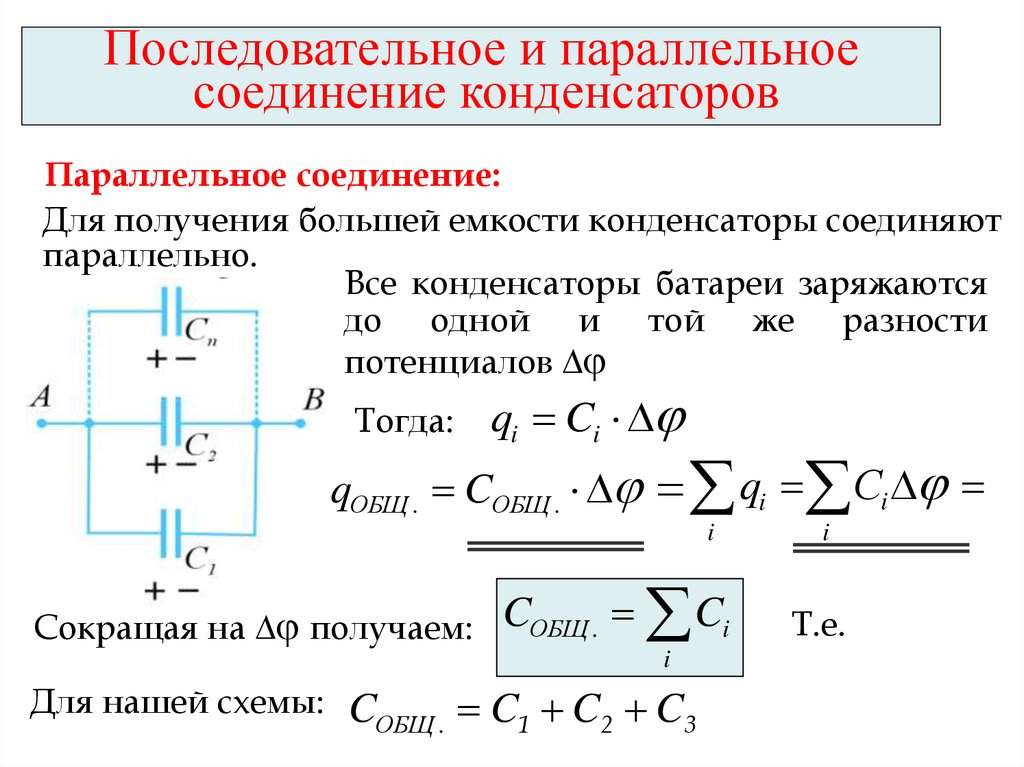
Последовательное и параллельноесоединение конденсаторов
Параллельное соединение:
Для получения большей емкости конденсаторы соединяют
параллельно.
Все конденсаторы батареи заряжаются
С1
до одной и той же разности
потенциалов
С2
Тогда: qi Ci
С3
qОБЩ . CОБЩ . qi Сi
i
Сокращая на получаем:
CОБЩ . Ci
i
Для нашей схемы:
CОБЩ . C1 C2 C3
i
Т.е.
20.
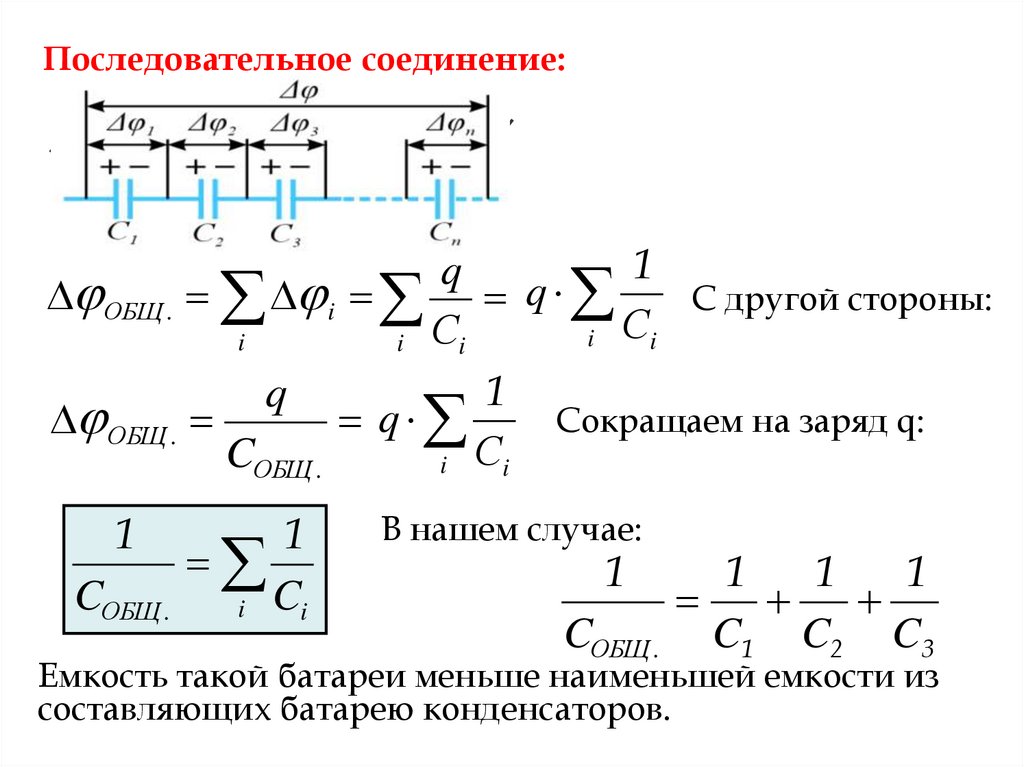
Последовательное соединение:С2
С3
С1
1
2
3
1
q
ОБЩ . i q
С другой стороны:
i Сi
i
i Сi
1
q
Сокращаем на заряд q:
ОБЩ .
q
CОБЩ .
i Сi
1
CОБЩ .
1
i Ci
В нашем случае:
1
CОБЩ .
1
1
1
C1 C2 C3
Емкость такой батареи меньше наименьшей емкости из
составляющих батарею конденсаторов.
21.
Энергия электрического поляСообщение проводнику электрического заряда связано с
совершением работы по преодолению кулоновских сил
отталкивания . Эта работа идет на увеличение энергии
заряженного проводника.
dA dq dq C d C d
Полная работа, необходимая для увеличения потенциала
проводника от 0 до , равна:
A C d
0
Следовательно, энергия
уединенного проводника:
C
2
C
q
q
W
2
2C
2
2
22.
q dqdA dq
q
C
q dq q 2 q 1 2
A
C
2C
2
0
Для заряженного конденсатора :
Учитывая, что конденсатор - это система из двух
проводников, у которых q1=+q, q2=-q, тогда:
1
W q1 1 q2 2
2
Вычислим энергию плоского конденсатора:
S
C 0
E d
d
2
1
1
C 1 2
2
W
0 Sd E 0 E E V
2
2
2
Объемная
W 1
1
E D плотность
W E D V
энергии.
V 2
2
23.
Пондермоторные силы – это силы электрическоговзаимодействия.
• Разноименные пластины конденсатора будут
притягиваться. Силу их притяжения называют
пондермоторной.
• При незначительном перемещении одной пластины в
поле другой совершается работа
dW
dA dW Fdx, F
dx
2
2
q
q dx
dW
.
2C 2ε 0εS
Тогда, можно записать, что
• Отсюда можно получить формулу для расчета
2
пондермоторной силы
q
F
2ε εS
.


















 physics
physics








