Similar presentations:
Методические указания к курсовому проекту по спецкурсу № 2. Теории ядерных реакторов
1.
Теория ядерныхреакторов
Методические указания к курсовому проекту
по спецкурсу № 2
Докладчик
Алексеенко
Николай Николаевич
к.ф.-м.н.
доцент
2. Тема проекта
РАСЧЕТ КРИТИЧЕСКИХ ПАРАМЕТРОВГОМОГЕННОГО ЯДЕРНОГО РЕАКТОРА
Состав активной зоны: графит и уран с отношением чисел ядер
235U/(235U+238U)=0.15.
Состав отражателя - торий.
Исполнитель студент гр. Фт-490202
Иванов Пётр Сидорович
14.01.2021
2
3. Цель проекта
1. Неформальное изучение основныхпонятий теории ядерных реакторов.
2. Ознакомление с методами расчета
реакторов.
3. Многогрупповой расчет критических
параметров реактора заданной
геометрии и состава.
4. Анализ полученных результатов.
14.01.2021
3
4. План работы
1.2.
3.
4.
Освежить в памяти лекции, по теории ядерных
реакторов.
По лекциям и методичке изучить расчет критических
параметров реактора методом Шихова-Новожилова.
В соответствии с заданием к курсовому проекту сделать
«вручную» расчет критических параметров реактора без
отражателя в нулевом приближении по 9-групповой
системе констант.
Произвести расчеты согласно индивидуальному
заданию по программе MSN. Изучить, полученные
вручную и по программе, результаты и написать отчет.
14.01.2021
4
5. План работы
5.6.
7.
Осмыслить полученные результаты и написать отчет в
соответствии с ГОСТ 7.32-2001.
В отчете должны быть разделы: оглавление, введение,
краткое описание методики расчета, результаты расчета,
обсуждение результатов расчета, список использованных
источников. Во введении нужно отразить существующие
методы расчета реакторов и обосновать применение
метода Шихова-Новожилова в курсовом проекте.
Подготовить презентацию работы и защитить проект.
14.01.2021
5
6. 1. Подготовка ядерных констант
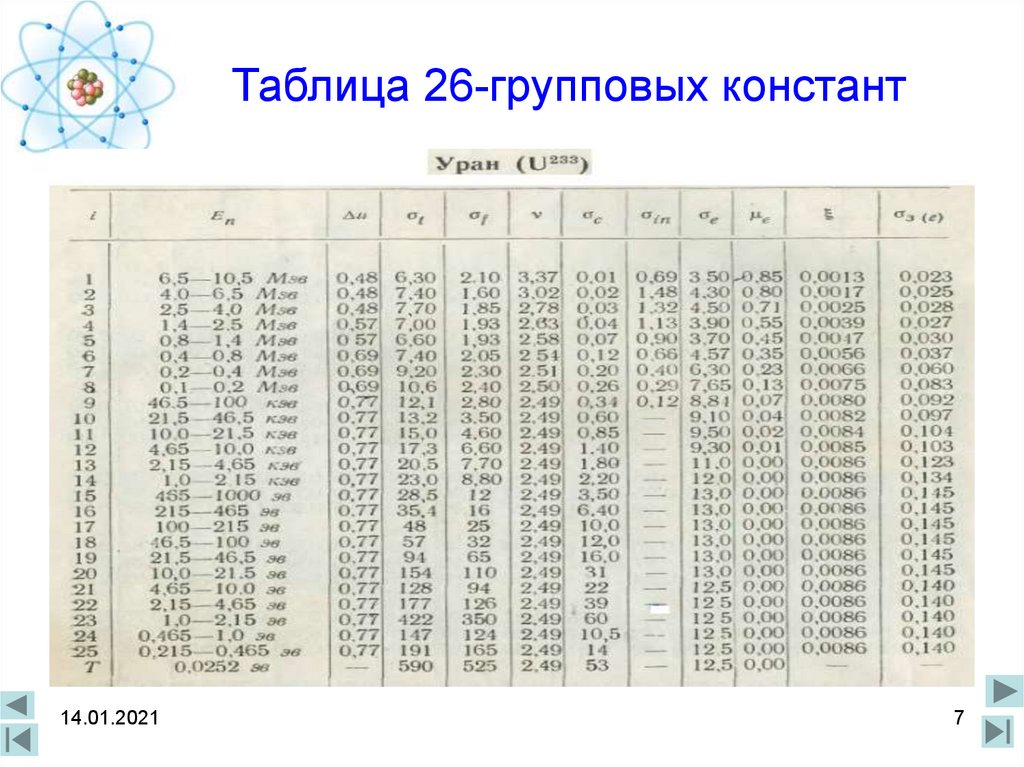
Для расчета используются 26-групповые ядерныеконстанты, из книги Л.П. Абагян и др.
С целью детального изучения методики расчета в
задании к проекту студентам предлагается сделать
самостоятельно расчет критических параметров
реактора сферической геометрии без отражателя
(в нулевом приближении) по 9-групповой системе
ядерных констант. Поэтому возникает
необходимость перевода 26-групповых констант в
9-групповые.
14.01.2021
6
7. Таблица 26-групповых констант
14.01.20217
8. Связь между константами 26-групповой и 9-групповой систем
1-4:
5-7:
8-10:
11-13:
14-16:
17-19:
20-22:
23-25:
26 :
1
2
3
4
5
6
7
8
9
Для расчета констант 1-й группы 9групповой системы используются
константы с 1-й по 4-ю группу 26групповой системы и т.д.
14.01.2021
Расчет констант выполняется по
формуле
u u u u
1 4
ik uik 1 1 2 2 3 3 4 4
u k 1
u 1 u 2 u 3 u 4
Здесь слева микроскопическое
сечение 1-й группы 9-групповой системы, а справа (в
формуле) соответствующие
сечения 26-групповой системы.
8
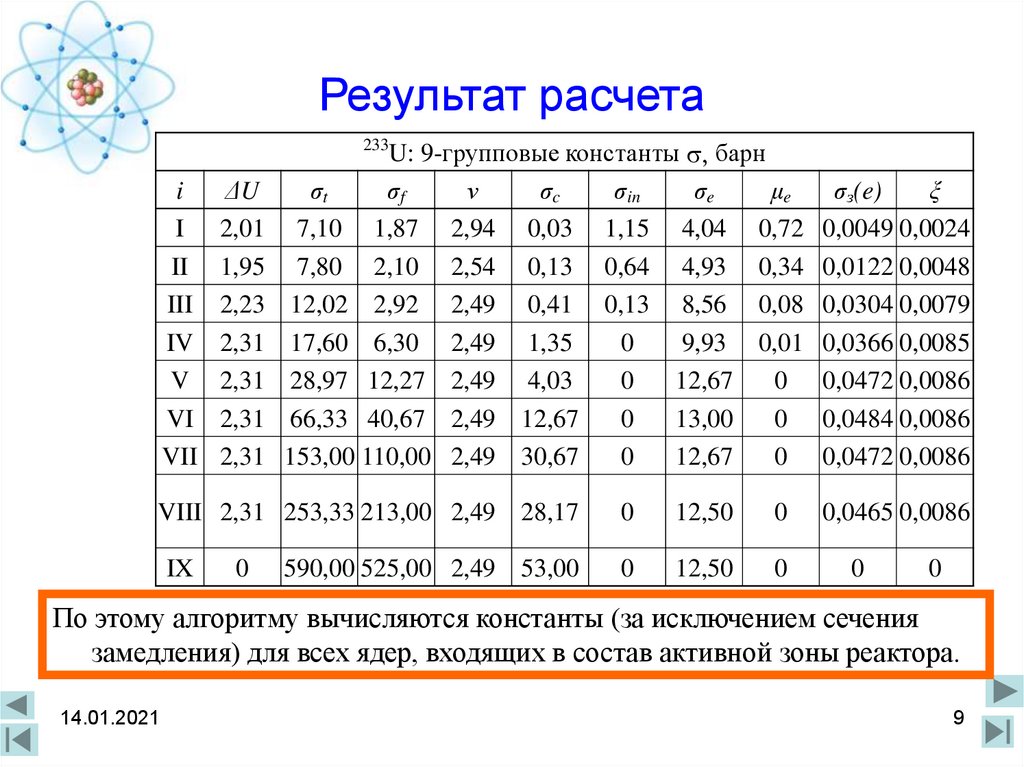
9. Результат расчета
U: 9-групповые константы , барнσt
σf
ν
σc
σin
σe
μe
7,10 1,87 2,94 0,03 1,15 4,04 0,72
7,80 2,10 2,54 0,13 0,64 4,93 0,34
12,02 2,92 2,49 0,41 0,13 8,56 0,08
17,60 6,30 2,49 1,35
0
9,93 0,01
28,97 12,27 2,49 4,03
0
12,67
0
66,33 40,67 2,49 12,67
0
13,00
0
153,00 110,00 2,49 30,67
0
12,67
0
233
i
I
II
III
IV
V
VI
VII
ΔU
2,01
1,95
2,23
2,31
2,31
2,31
2,31
VIII 2,31 253,33 213,00 2,49 28,17
IX
0
590,00 525,00 2,49 53,00
0
12,50
0
0
12,50
0
σз(e)
ξ
0,0049 0,0024
0,0122 0,0048
0,0304 0,0079
0,0366 0,0085
0,0472 0,0086
0,0484 0,0086
0,0472 0,0086
0,0465 0,0086
0
0
По этому алгоритму вычисляются константы (за исключением сечения
замедления) для всех ядер, входящих в состав активной зоны реактора.
14.01.2021
9
10. Расчет сечения замедления
Сечение замедления нейтронов определенной группы зависит не толькоот эффективных сечений среды, но и от формы внутри-группового
спектра, и от ширины группы. Поэтому, в отличие от других
групповых констант, сечение замедления нейтронов может
существенно изменяться в зависимости от формы группового спектра
даже в том случае, если все элементарные сечения в пределах группы
от энергии не зависят. Поэтому для расчета сечения замедления при
упругом рассеянии используем предварительно рассчитанные 9групповые константы упругого рассеяния и рассчитываем сечение
замедления по формуле
з (e)
e
u
b ,
где величины в правой части являются 9-групповыми, а
величину b будем считать равной единице.
14.01.2021
10
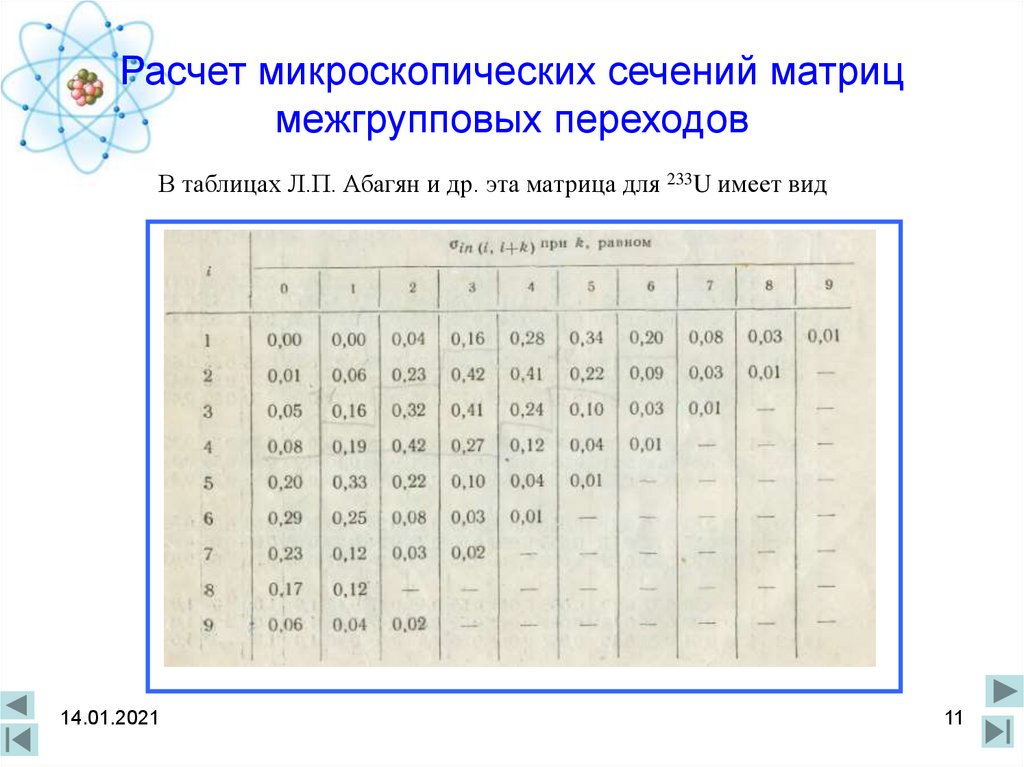
11. Расчет микроскопических сечений матриц межгрупповых переходов
В таблицах Л.П. Абагян и др. эта матрица для 233U имеет вид14.01.2021
11
12. Матрица межгрупповых переходов
• В этой таблице содержатся сечения неупругого рассеяниянейтронов, в результате которого нейтрон, теряя энергию
переходит из группы i в группу j. При этом i ≤ j.
• В первом столбце k=0, i = j находятся диагональные
элементы матрицы.
• Диагональные элементы определяют вероятность того, что
в результате неупругого рассеяния нейтрона на ядре 233U
энергия нейтрона останется в пределах той же группы, в
которой он находился до рассеяния.
14.01.2021
12
13. Расчет 9-групповой матрицы рассеяния
Он проводится по формулеii
'
1
u i
ni
n'
kl
u
ik ii
'
k 1
l 1
Для расчета по этой формуле 26-групповую матрицу нужно
представить в привычном виде, где поддиагональные
элементы нулевые, а диагональные и наддиагональные
могут отличаться от нуля.
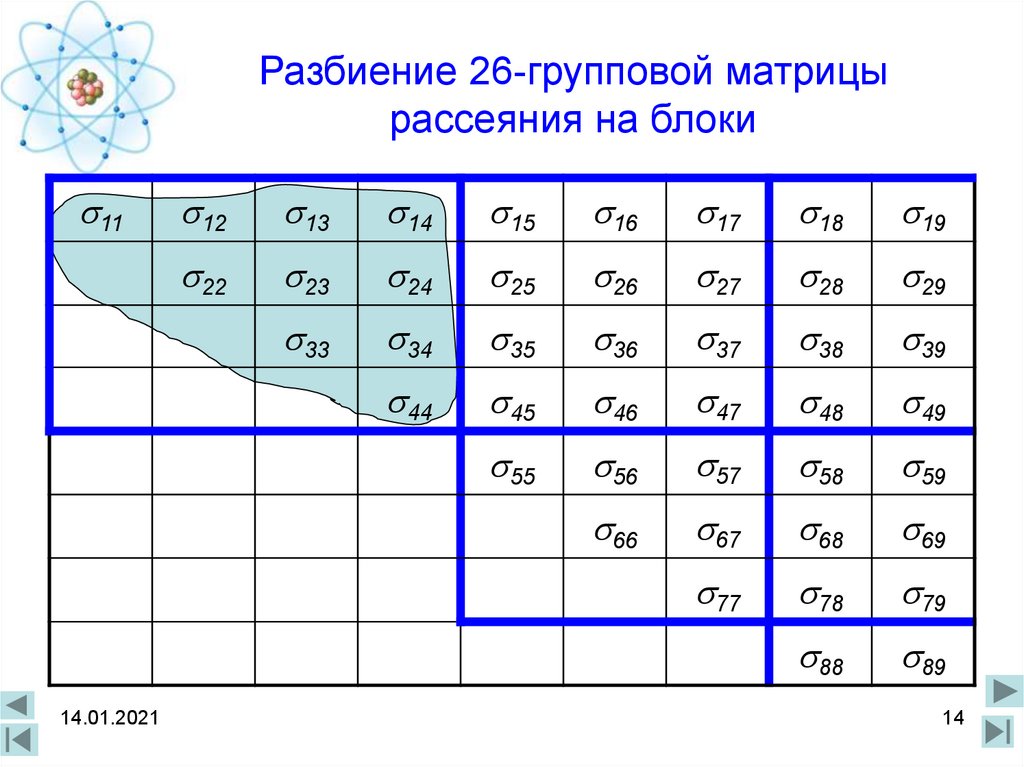
После этого её нужно разделить на блоки в соответствии со
следующим слайдом.
14.01.2021
13
14. Разбиение 26-групповой матрицы рассеяния на блоки
1114.01.2021
12
13
14
15
16
17
18
19
22
23
24
25
26
27
28
29
33
34
35
36
37
38
39
44
45
46
47
48
49
55
56
57
58
59
66
67
68
69
77
78
79
88
89
14
15. Вычисление 9-групповой матрицы рассеяния
Расчет проводится по формуле, представленной на слайде 11.Развернём её для трёх элементов 9-групповой матрицы:
I,9I
I,9II
( 11 12 13 14 ) u1 ( 22 23 24 ) u2 ( 33 34 ) u3 44 u4
(3)
u1 u2 u3 u4
( 15 16 17 ) u1 ( 25 26 27 ) u2 ( 35 36 37 ) u3 ( 45 46 47 ) u4
(3' )
u1 u2 u3 u4
II,9 II
( 55 56 57 ) u5 ( 66 67 ) u6 77 u7 ''
(3 )
u5 u6 u7
По этим формулам вычисляются матрицы рассеяния для
всех ядер, входящих в состав активной зоны реактора.
14.01.2021
15
16. 2. Расчет макроскопических сечений
Макроскопическое сечение – это сумма произведений чисел ядер вединице объёма активной зоны (отражателя) на их микроскопические
сечения.
Пример. Пусть в активной зоне гомогенного реактора содержится 235U,
238U и 12C. Требуется вычислить макроскопическое сечение полного
взаимодействия нейтронов с ядрами. Это можно сделать по формуле
Σ t t8 N 8 t5 N 5 tc N c
(4)
Для расчета по формуле (4) необходимо определить числа ядер в
единице объема в активной зоны и отражателя для всех элементов.
14.01.2021
16
17. 3. Расчет числа ядер
Согласно проектному заданию в составе активной зоны содержатся 3компонента – делящийся элемент, сырьевой элемент и разбавитель (в
частности – замедлитель). Поэтому, имеет смысл в расчет чисел ядер
ввести величину обогащения топлива β по делящемуся компоненту и
величину разбавления топлива .
N1
,
N1 N 2
(5)
где
N1 – число ядер делящегося компонента в единице объема среды
(235U, 233U или Pu);
N2 - число ядер сырьевого компонента в единице объема среды (238U,
232Th).
14.01.2021
17
18. 3. Расчет числа ядер
Из (5) следует, чтоN1
,
N2 1
(6)
а разбавление, т.е. отношение числа ядер замедлителя к числу ядер
горючего
Nз
Nз
.
N г N1 N 2
(7)
Отсюда
Nз
.
N1
14.01.2021
(8)
18
19. 3. Расчет числа ядер
Объём, занимаемый всеми компонентами активной зоны в единицеобъёма смеси должен быть равен единице
V1 V2 V3 1
(9)
или
N1 A1 N 2 A2 N 3 A3
1,
N 0 1 N 0 2 N 0 3
N1 A1 1 A2 A3
1 .
N 0 1
2 3
(10)
(11)
Здесь N0 – число Авогадро; Ai и Ni – молярная масса и число ядер
соответствующего компонента в единице объема.
14.01.2021
Отсюда
19
20. 3. Расчет числа ядер
N0N1
.
A1 1 A2 A3
1
N 2 N1
2
1
N3 ( N1 N 2 ) .
(12)
3
.
(13)
(14)
Для расчета чисел ядер можно воспользоваться электронной таблицей
(файл «Число_ядер»).
Расчет макросечений проводится по формуле (4).
14.01.2021
20
21. Расчет других макроконстант
Для расчета макросечения увода в методичке имеется две формулы –(2.13) и (2.15). Следует пользоваться формулой (2.15). Если в состав
реактора входит вода, то следует вычислять макроскопические
матрицы упругого и неупругого рассеяния.
Для расчета элементов 9-группового спектра деления применяется
суммирование элементов 26-группового спектра. Например, для
первой и второй групп 9-групповой системы констант можно записать
1
2
3
4
91 26
26
26
26
,
5
6
7
92 26
26
26
.
14.01.2021
21
22. 4. Расчет потоков и ценностей
Потоки и ценности вычисляются по формулам (1.10) и (1.11)методички.
j 1
aj 0
a 0j
и
j
a0
j
fa
l 1
j
fa
,
j
ув a
(1.10)
m j l
j
fa
l j
a la 0
j
0
l
a a0
l j 1
j
увa
.
(1.11)
- соответственно доля нейтронов j-й группы в спектре деления и
число нейтронов, образующееся при делении.
Распишем эти формулы для трех начальных групп нейтронов.
Поток для первой группы
1
a0
14.01.2021
1a
1увa
22
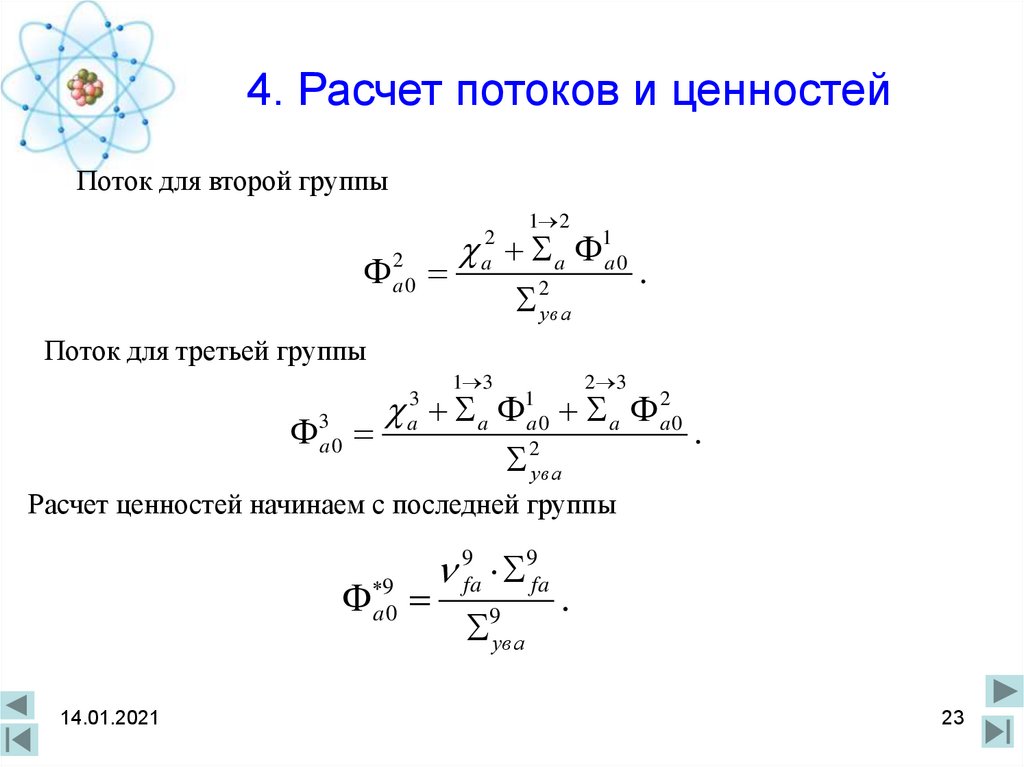
23. 4. Расчет потоков и ценностей
Поток для второй группы2a 0
1 2
a 1a 0
2
a
2
увa
.
Поток для третьей группы
3a 0
1 3
2 3
a a 2a 0
3
a
1
a0
2
увa
.
Расчет ценностей начинаем с последней группы
a90
14.01.2021
9fa 9fa
9
увa
.
23
24. 4. Расчет потоков и ценностей
Ценность для восьмой группыa80
8
fa
Ценность для седьмой группы
a70
8 9
a *a80
8
fa
7 8
8
увa
7 9
a a *a90
7
fa
7
fa
*8
a0
.
7
увa
.
Важно отметить, что в сечения межгрупповых переходов, входящие в эти
формулы, должны входить сечения замедления. Например,
7 8
a in78 7з (e).
14.01.2021
24
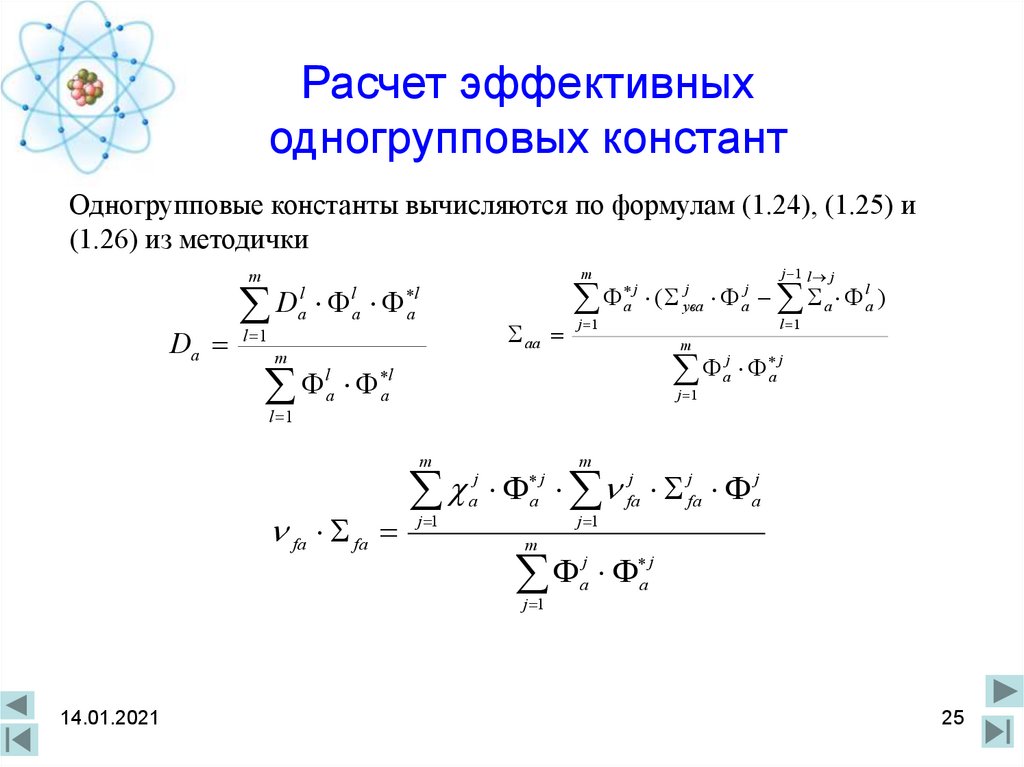
25. Расчет эффективных одногрупповых констант
Одногрупповые константы вычисляются по формулам (1.24), (1.25) и(1.26) из методички
m
Da
D
l
a
l
a
m
l
a
aa
l 1
m
l
a
j
a
(
j
увa
j 1
l 1
m
l
a
j 1 l j
a la )
j
a
j
a
a j
j 1
l 1
m
fa fa
j 1
j
a
m
faj jfa aj
j
a
j 1
m
j
j
a a
j 1
14.01.2021
25
26. Расчет критических параметров
Критический радиус находим из условия равенства геометрического иматериального параметров
2
2
кр
R
14.01.2021
fa fa aa
Da
.
26




















 physics
physics








