Similar presentations:
Сравнение десятичных дробей
1. Сравнение десятичных дробей.
2. Сравните:
569 и 98367 и 371
5/9 и 2/9
3/10 и 30/100
3. Проверь себя
569 > 98367 < 371
5/9 > 2/9
3/10 = 30/100
4.
Так как 3/10 = 30/100а
3/10 = 0,3
30/100 = 0,30
то
0,3 = 0,30
5. Вывод
1.Если к десятичной дроби приписатьсправа какое угодно число нулей, то
получится дробь, равная данной.
0,7 = 0,70 = 0,700;
141 = 141,0 = 141,00 = 141,000
2.Если в десятичной дроби последние
цифры – нули, то, отбросив их, получим
дробь, равную данной.
26,100 = 26,10 = 26,1.
6. Напишите десятичную дробь
• а) с четырьмя знаками после запятой,равную 0,87
• б) с тремя знаками после запятой,
равную 35
• в) с двумя знаками после запятой,
равную 8,40000
7. Проверь себя
• а) 0,87 = 0,8700• б) 35 = 35,000
• в) 8,40000 = 8,40
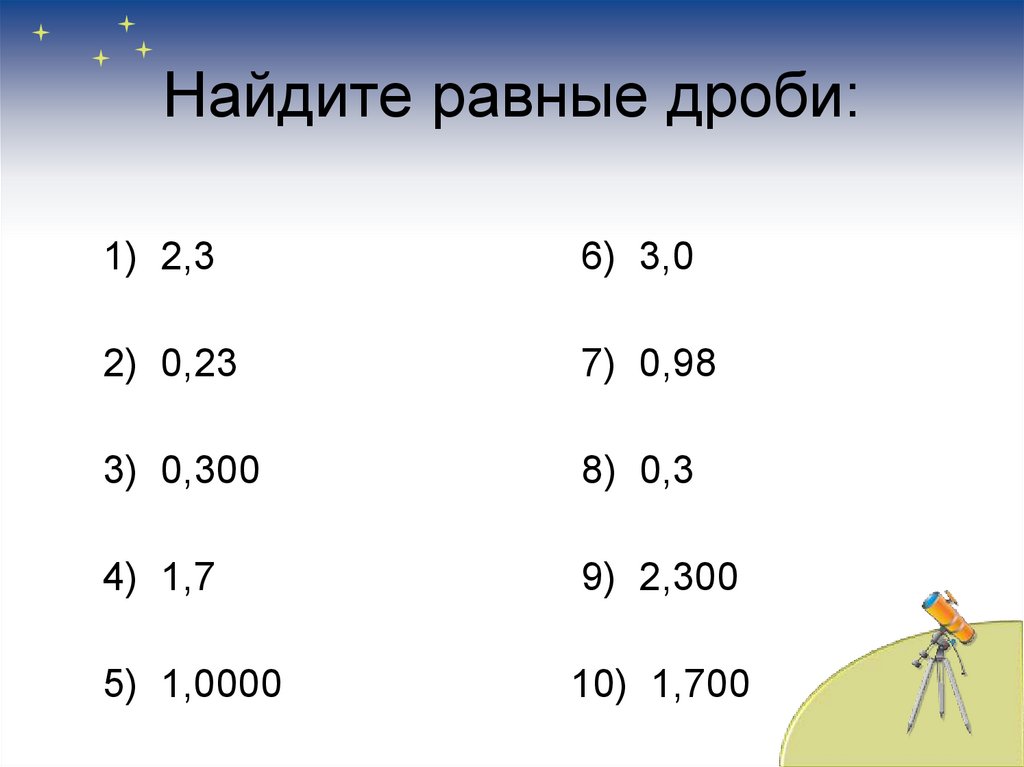
8. Найдите равные дроби:
1) 2,36) 3,0
2) 0,23
7) 0,98
3) 0,300
8) 0,3
4) 1,7
9) 2,300
5) 1,0000
10) 1,700
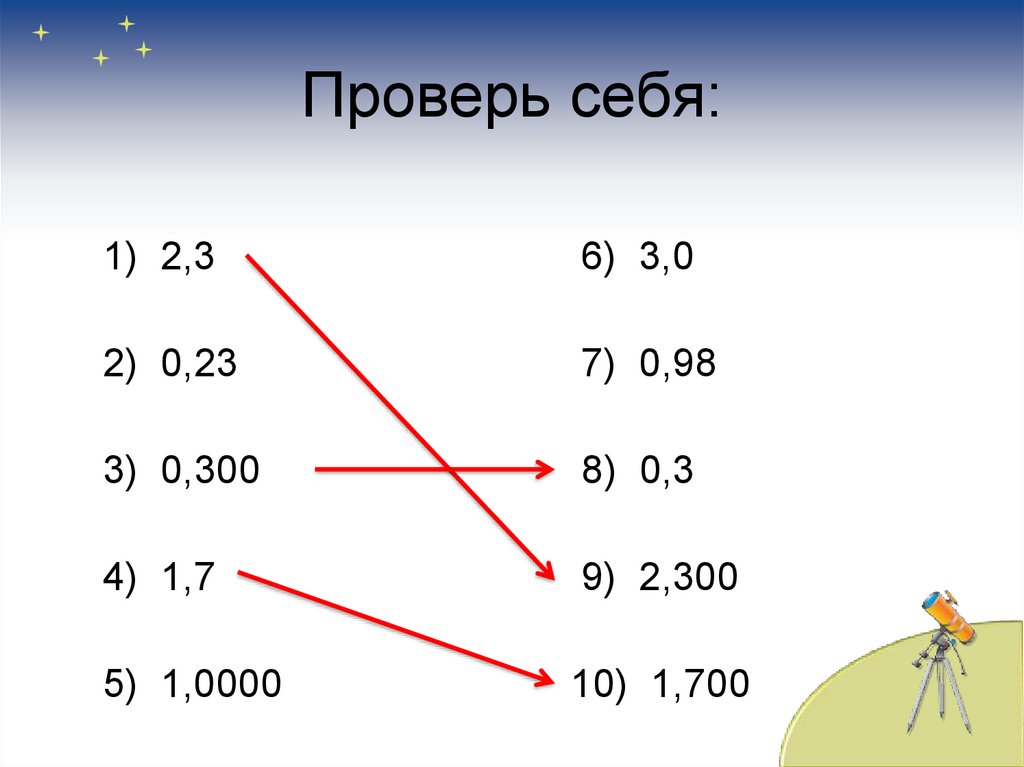
9. Проверь себя:
1) 2,36) 3,0
2) 0,23
7) 0,98
3) 0,300
8) 0,3
4) 1,7
9) 2,300
5) 1,0000
10) 1,700
10. Десятичные дроби, как и натуральные числа, сравниваем по разрядам. Если целые части десятичных дробей различны, то больше та
Алгоритм сравнения десятичныхдробей
Десятичные дроби, как и натуральные
числа, сравниваем по разрядам.
Если целые части десятичных дробей
различны, то больше та дробь, у
которой больше целая часть.
Если целые части десятичных дробей
одинаковы, то больше та дробь, у
которой больше первый из несовпавших
разрядов после запятой.
11. Сравним дроби: 3,12 и 5,4
• Сравниваем целые части 3 и 5: 3 < 5• значит
3,12 < 5,4
12. Сравним дроби: 2,67 и 2,8
• Сравниваем целые части 2 и 2: 2 = 2• сравниваем десятые 6 и 8:
• значит
6< 8
2,67 < 2,8
13. Сравним дроби: 1,8 и 1,82
• Уравняем число разрядов, приписав кпервой дроби цифру 0 : 1,80 и 1,82
• Сравниваем целые части 1 и 1: 1 = 1
• сравниваем десятые 8 и 8:
8=8
• сравниваем сотые 0 и 2:
0<2
значит
1,8 < 1,82
14. Алгоритм сравнения десятичных дробей
Десятичные дроби, как и натуральные числа,сравниваем по разрядам.
Если целые части десятичных дробей
различны, то больше та дробь, у которой
больше целая часть.
Если целые части десятичных дробей
одинаковы, то больше та дробь, у которой
больше первый из несовпавших разрядов
после запятой.
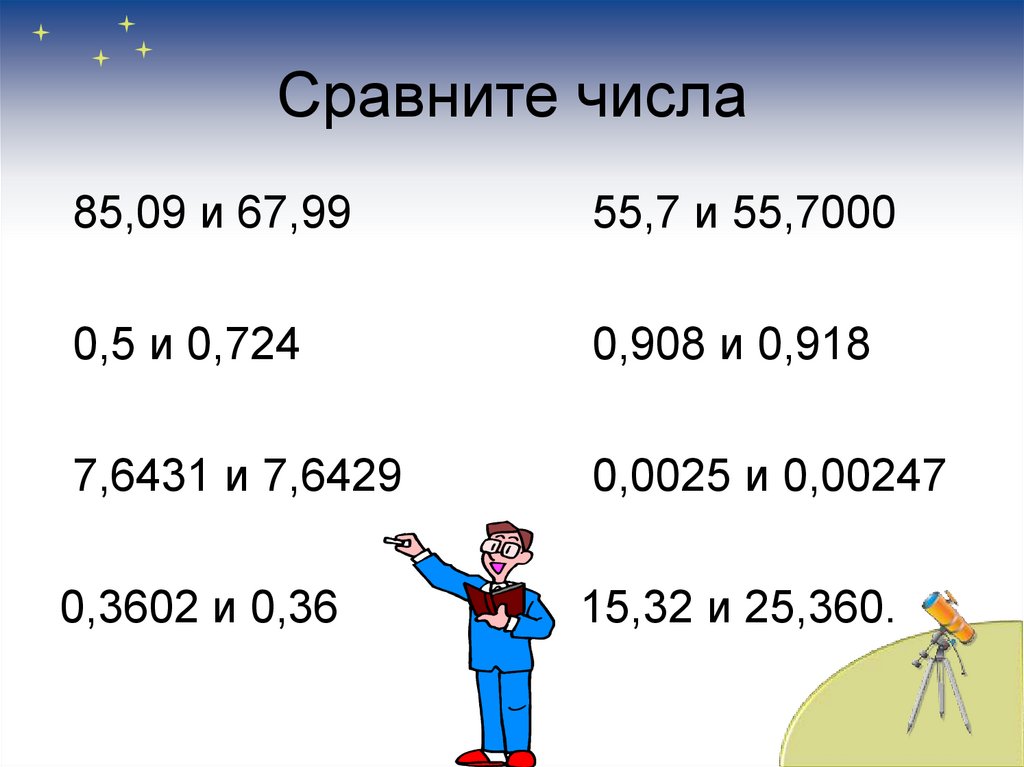
15. Сравните числа
85,09 и 67,9955,7 и 55,7000
0,5 и 0,724
0,908 и 0,918
7,6431 и 7,6429
0,0025 и 0,00247
0,3602 и 0,36
15,32 и 25,360.
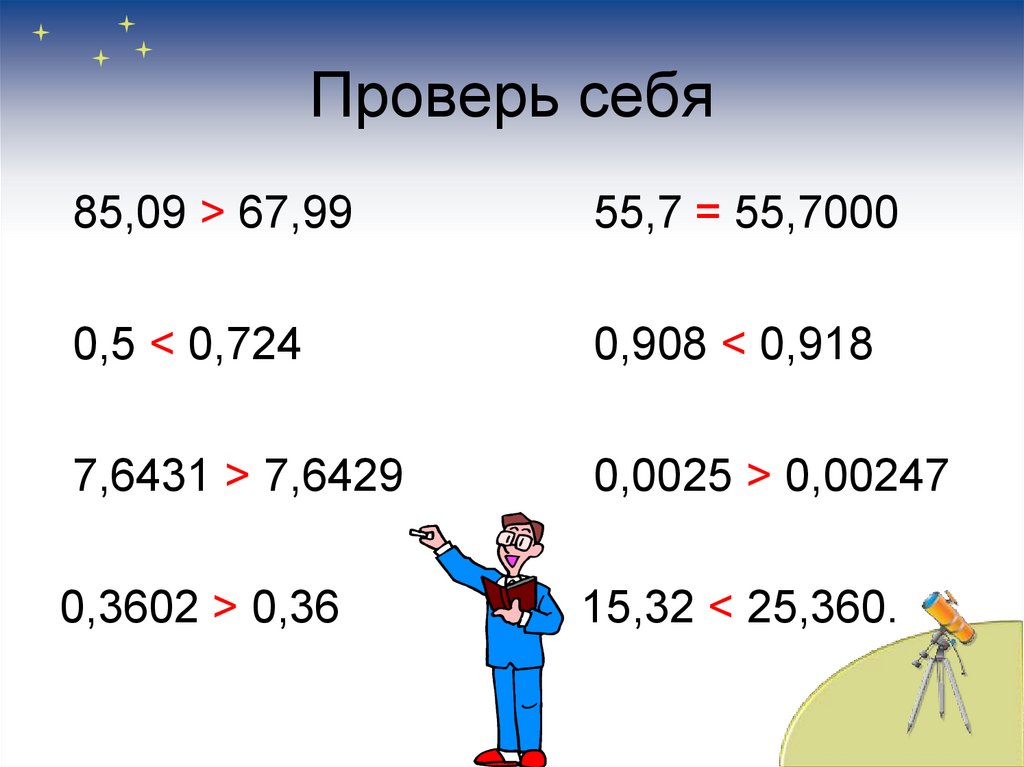
16. Проверь себя
85,09 > 67,9955,7 = 55,7000
0,5 < 0,724
0,908 < 0,918
7,6431 > 7,6429
0,0025 > 0,00247
0,3602 > 0,36
15,32 < 25,360.
17. Расположите числа в порядке убывания
а) 7,34; 7,4; 7,3б) 2,356; 2,35; 2,36
18. Проверь себя
а) 7,4; 7,34; 7,3б) 2,36; 2,356; 2,35
19. Замените значок « ⃰ » цифрой так, чтобы полученная запись была верной:
1) 5,688 < 5,6*1;2) 71,09* < 71,091;
3) 9,*57 > 9,499;
20. Проверь себя:
1) 5,688 < 5,691;2) 71,090 < 71,091;
3) 9,557 > 9,499;
21. Самостоятельная работа Из верных равенств составьте слово:
М)14,2 < 14,20С) 8,7 > 8,608
О)10,72 < 10,69
Е) 0,095 < 0,1
Р)8,547 > 8,474
А) 14,13 > 12,13
Н) 3,7 > 3,666
И) 0,37 > 0,368
В)72,03 < 72,18
Н) 37,24 < 38,24
К) 1,3 < 1,237
Е) 5,603 > 5,6
22. Проверь себя Из верных равенств составьте слово:
М)14,2 = 14,20С) 8,7 > 8,608 +
О)10,72 > 10,69
Е) 0,095 < 0,1 +
Р)8,547 > 8,474 +
А) 14,13 > 12,13 +
Н) 3,7 > 3,666 +
И) 0,37 > 0,368 +
В)72,03 < 72,18 +
Н) 37,24 < 38,24 +
К) 1,3 > 1,237
Е) 5,603 > 5,6
Ответ: сравнение
+


















 mathematics
mathematics








