Similar presentations:
Кривые линии и поверхности
1.
Лекция 5КРИВЫЕ ЛИНИИ
И ПОВЕРХНОСТИ
2.
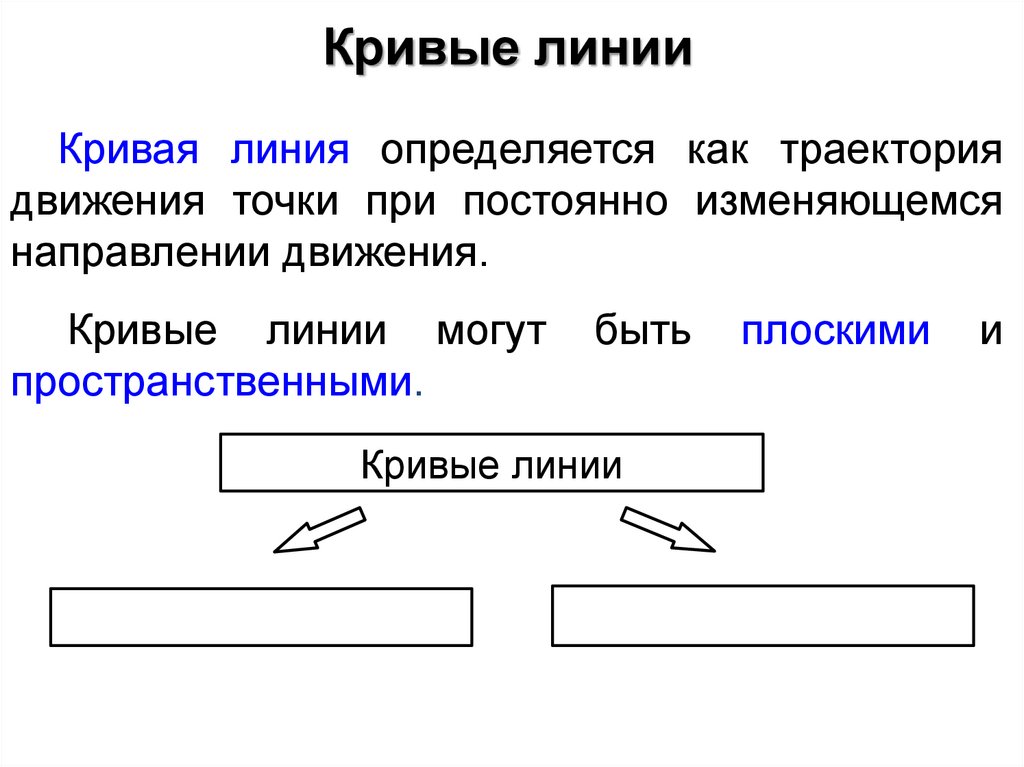
Кривые линии3.
Кривые линииКривая линия определяется как траектория
движения точки при постоянно изменяющемся
направлении движения.
4.
Кривые линииКривая линия определяется как траектория
движения точки при постоянно изменяющемся
направлении движения.
Кривые линии могут
пространственными.
быть
плоскими
и
5.
Кривые линииКривая линия определяется как траектория
движения точки при постоянно изменяющемся
направлении движения.
Кривые линии могут
пространственными.
быть
Кривые линии
1. Плоскости уровня
плоскими
и
6.
Кривые линииКривая линия определяется как траектория
движения точки при постоянно изменяющемся
направлении движения.
Кривые линии могут
пространственными.
быть
Кривые линии
1. Плоскости
уровня
1. Плоские
плоскими
и
7.
Кривые линииКривая линия определяется как траектория
движения точки при постоянно изменяющемся
направлении движения.
Кривые линии могут
пространственными.
быть
плоскими
Кривые линии
1. Плоскости
уровня
1. Плоские
2. Пространственные
и
8.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
9.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
__________
__________
__________
__________
10.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
Окружность
__________
__________
__________
__________
11.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
Окружность
__________
Эллипс
__________
__________
__________
12.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
Окружность
__________
Эллипс
__________
Парабола
__________
__________
13.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
Окружность
__________
Эллипс
__________
Парабола
__________
Гипербола
__________
14.
Все точки плоской линии лежат в однойплоскости,
например,
окружность,
эллипс,
парабола, гипербола, спираль Архимеда и т.д.
Окружность
__________
Эллипс
__________
Парабола
__________
Гипербола
__________
Кривая
называется
алгебраической,
если описывается каким-либо уравнением.
15.
Плоские алгебраические кривыеЛЕМНИСКАТА
ТРЕХЛЕПЕСТКОВАЯ
РОЗА
ЦИКЛОИДА
ЧЕТЫРЕХЛЕПЕСТКОВАЯ
РОЗА
ЭВОЛЬВЕНТА ЭЛЛИПСА
КАРДИОИДА
ДЕКАРТОВ ЛИСТ
ЭВОЛЬВЕНТА ОКРУЖНОСТИ
ЦИССОИДА ДИОКЛА
СПИРАЛЬ АРХИМЕДА
16.
Пространственные кривые17.
Пространственные кривыеПространственные кривые линии это те
линии, у которых точки не лежат в одной
плоскости.
18.
Пространственные кривыеПространственные кривые линии это те
линии, у которых точки не лежат в одной
плоскости.
Например, винтовая линия. Винтовая
линия может быть цилиндрической и
конической.
19.
Пространственные кривыеПространственные кривые линии это те
линии, у которых точки не лежат в одной
плоскости.
Например, винтовая линия. Винтовая
линия может быть цилиндрической и
конической.
20.
Цилиндрическая винтовая линия21.
Цилиндрическая винтовая линияЦилиндрическая
винтовая
линия
образуется
путем
движения
точки,
совершающей
равномерно-поступательное
движение по прямой, параллельной некоторой
оси, вокруг которой прямая, в свою очередь,
вращается равномерно.
22.
Цилиндрическая винтовая линияЦилиндрическая
винтовая
линия
образуется
путем
движения
точки,
совершающей
равномерно-поступательное
движение по прямой, параллельной некоторой
оси, вокруг которой прямая, в свою очередь,
вращается равномерно.
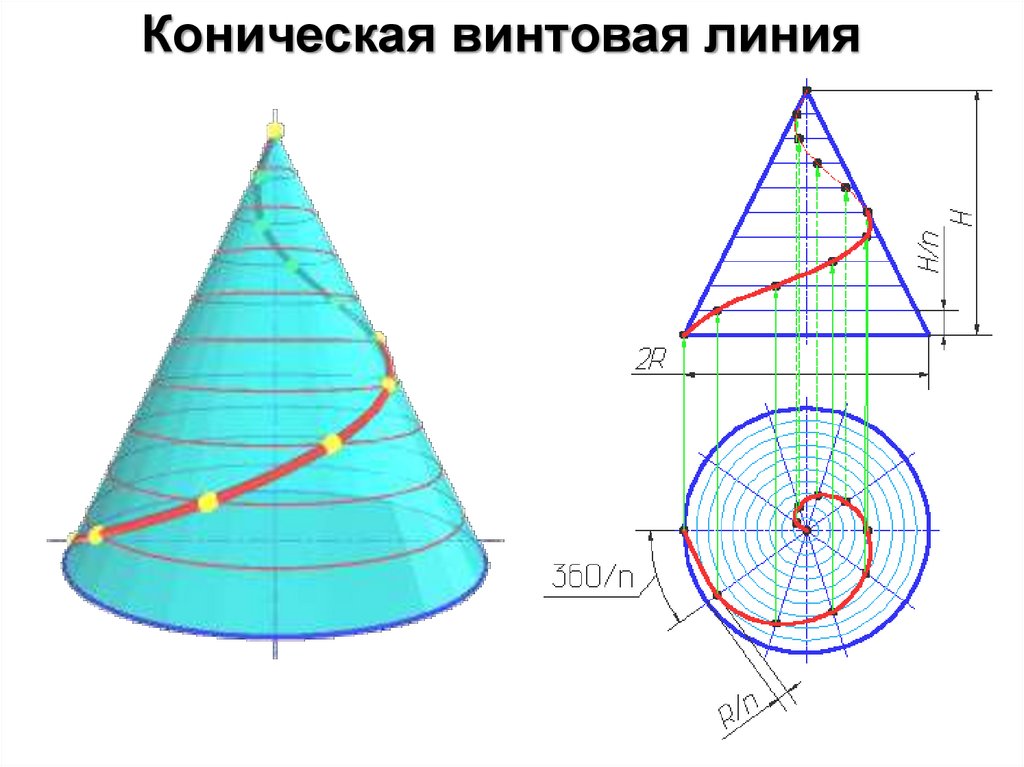
Коническая винтовая линия
23.
Цилиндрическая винтовая линияЦилиндрическая
винтовая
линия
образуется
путем
движения
точки,
совершающей
равномерно-поступательное
движение по прямой, параллельной некоторой
оси, вокруг которой прямая, в свою очередь,
вращается равномерно.
Коническая винтовая линия
Траекторию
точки,
движущейся
по
образующей вращающегося вокруг своей оси
прямого
кругового
конуса,
называют
конической винтовой линией.
24.
25.
Коническая винтовая линия26. Кривые поверхности
27. Кривые поверхности
Поверхность - это совокупность всехпоследовательных положений некоторой
перемещающейся в пространстве линии.
28. Кривые поверхности
Поверхность - это совокупность всехпоследовательных положений некоторой
перемещающейся в пространстве линии.
Линию, производящую поверхность, в
каждом
ее
положении
называют
образующей,
а
линию,
по
которой
перемещается
образующая,
называют
направляющей.
29.
Поверхности1. Плоскости уровня
30.
ПоверхностиЛинейчатые
1. Плоскости
уровня
31.
ПоверхностиЛинейчатые
1. Плоскости
уровня
Нелинейчатые (кривые)
32.
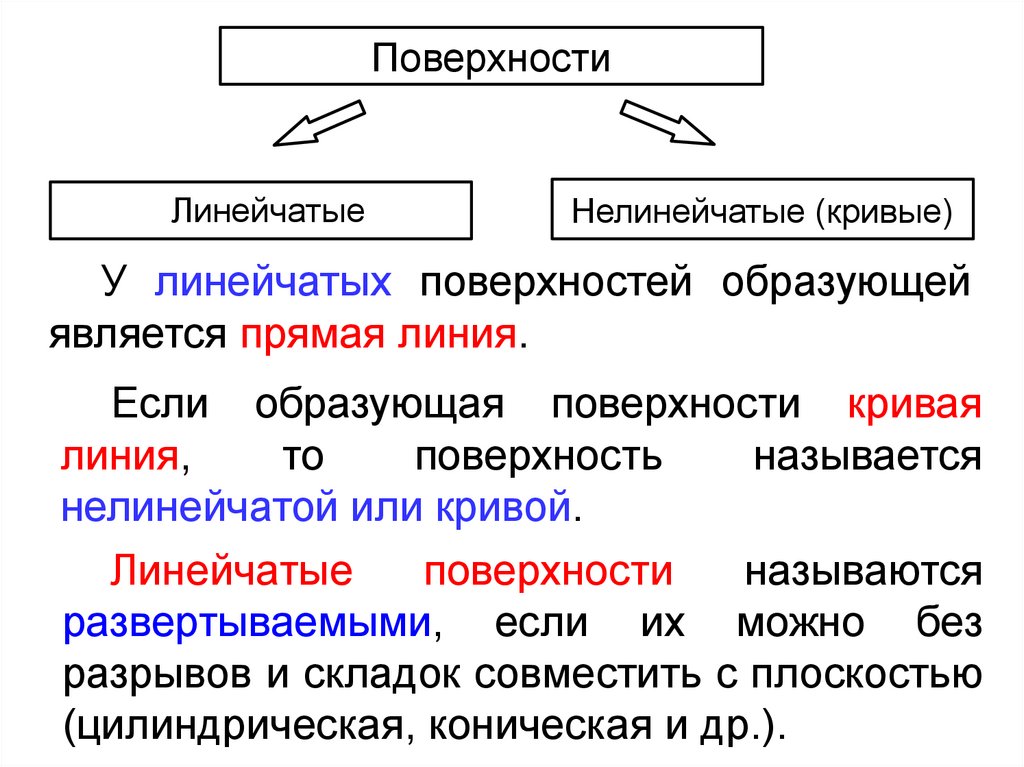
ПоверхностиЛинейчатые
1. Плоскости
уровня
Нелинейчатые (кривые)
У линейчатых поверхностей образующей
является прямая линия.
33.
Линейчатые поверхности(образующей является прямая линия)
34.
Линейчатые поверхности(образующей является прямая линия)
ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ
образуется прямой линией, сохраняющей во
всех своих положениях параллельность
некоторой прямой линии и проходящей
последовательно
через
все
точки
направляющей.
35.
Линейчатые поверхности(образующей является прямая линия)
ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ
образуется прямой линией, сохраняющей во
всех своих положениях параллельность
некоторой прямой линии и проходящей
последовательно
через
все
точки
направляющей.
36.
КОНИЧЕСКАЯ ПОВЕРХНОСТЬобразуется прямой линией, проходящей через
некоторую неподвижную точку и через все
точки направляющей a. Неподвижная точка
S - вершина конической поверхности.
37.
КОНИЧЕСКАЯ ПОВЕРХНОСТЬобразуется прямой линией, проходящей через
некоторую неподвижную точку и через все
точки направляющей a. Неподвижная точка
S - вершина конической поверхности.
38.
ПоверхностиЛинейчатые
1. Плоскости
уровня
Нелинейчатые (кривые)
У линейчатых поверхностей образующей
является прямая линия.
Если образующая поверхности кривая
линия,
то
поверхность
называется
нелинейчатой или кривой.
39.
ПоверхностиЛинейчатые
1. Плоскости
уровня
Нелинейчатые (кривые)
У линейчатых поверхностей образующей
является прямая линия.
Если образующая поверхности кривая
линия,
то
поверхность
называется
нелинейчатой или кривой.
Линейчатые
поверхности
называются
развертываемыми, если их можно без
разрывов и складок совместить с плоскостью
(цилиндрическая, коническая и др.).
40.
41.
Поверхности вращения42.
Поверхности вращенияПоверхностью вращения называют
поверхность, получаемую вращением
какой-либо образующей линии вокруг
неподвижной
прямой
оси
поверхности.
43.
Поверхности вращенияПоверхностью вращения называют
поверхность, получаемую вращением
какой-либо образующей линии вокруг
неподвижной
прямой
оси
поверхности.
Поверхность вращения можно
задать образующей и положением
оси.
44.
Поверхности вращенияПоверхностью вращения называют
поверхность, получаемую вращением
какой-либо образующей линии вокруг
неподвижной
прямой
оси
поверхности.
Поверхность вращения можно
задать образующей и положением
оси.
Каждая
точка
образующей
описывает окружность.
45.
Плоскость, перпендикулярная к осивращения, пересекает поверхность по
окружности.
46.
Плоскость, перпендикулярная к осивращения, пересекает поверхность по
окружности.
Такие
окружности
называют
параллелями.
47.
Плоскость, перпендикулярная к осивращения, пересекает поверхность по
окружности.
Такие
окружности
называют
параллелями.
Наибольшая
параллель
называется
экватором, наименьшая – горлом.
48.
Плоскость, перпендикулярная к осивращения, пересекает поверхность по
окружности.
Такие
окружности
называют
параллелями.
Наибольшая
параллель
называется
экватором, наименьшая – горлом.
Плоскость, проходящая через ось
вращения, называется меридиональной.
49.
Плоскость, перпендикулярная к осивращения, пересекает поверхность по
окружности.
Такие
окружности
называют
параллелями.
Наибольшая
параллель
называется
экватором, наименьшая – горлом.
Плоскость, проходящая через ось
вращения, называется меридиональной.
Линии, по которым эта плоскость
пересекает
поверхность
вращения,
называют образующими или меридианами.
50.
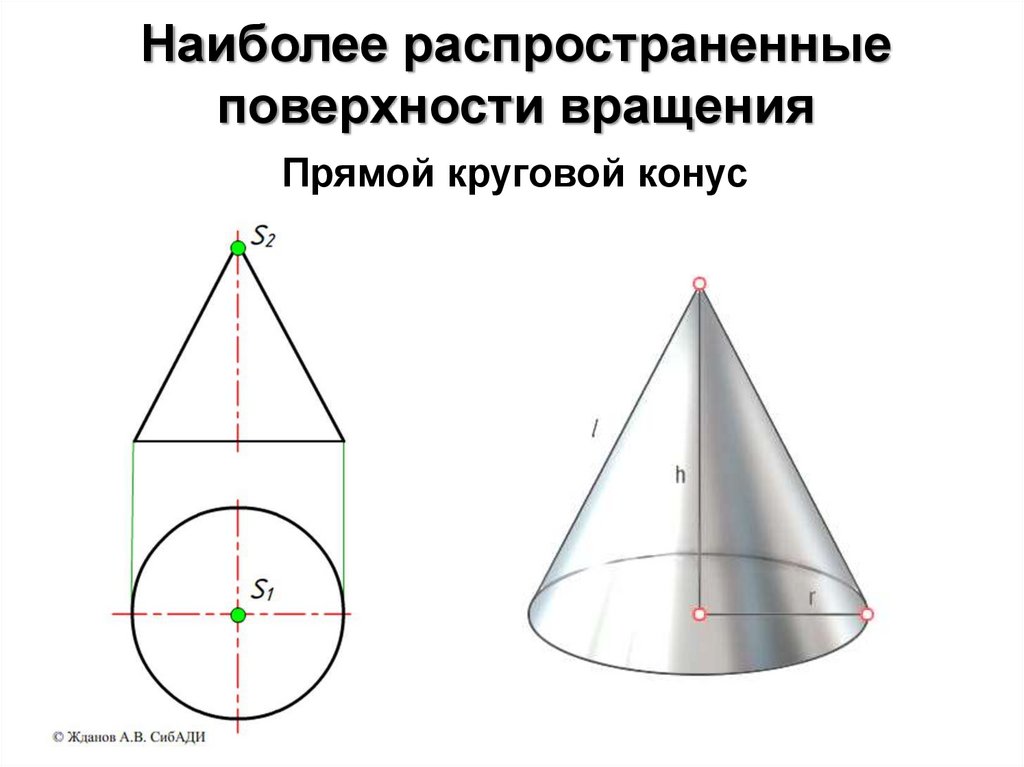
Наиболее распространенныеповерхности вращения
51.
Наиболее распространенныеповерхности вращения
Прямой круговой конус
52.
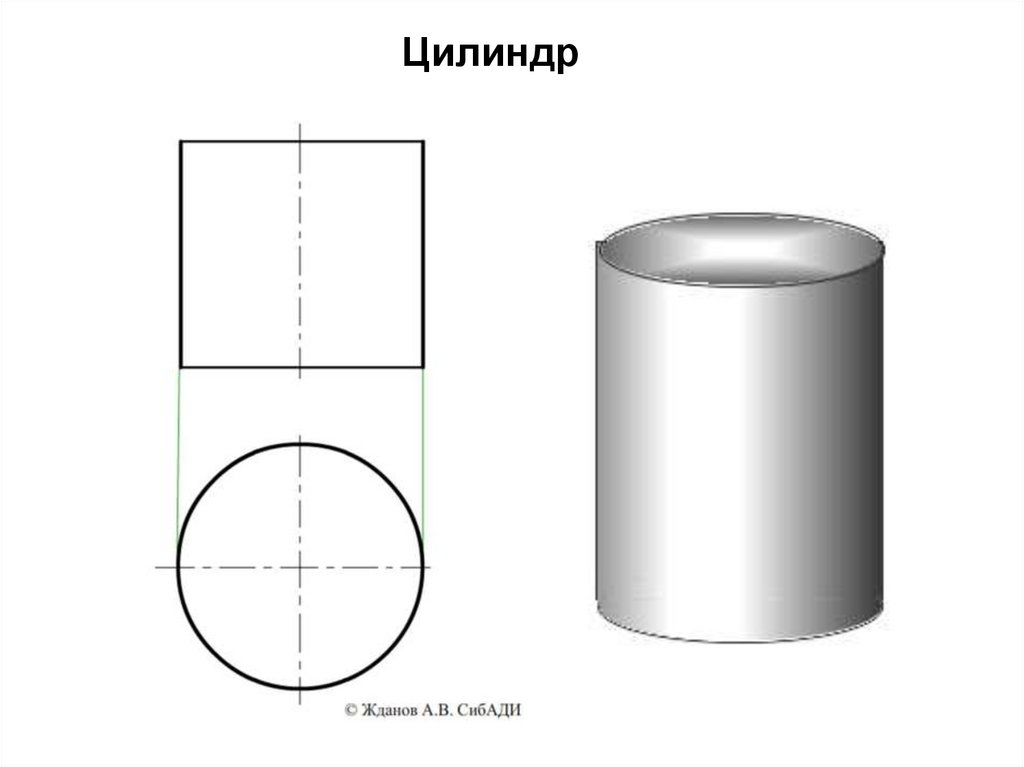
Цилиндр53.
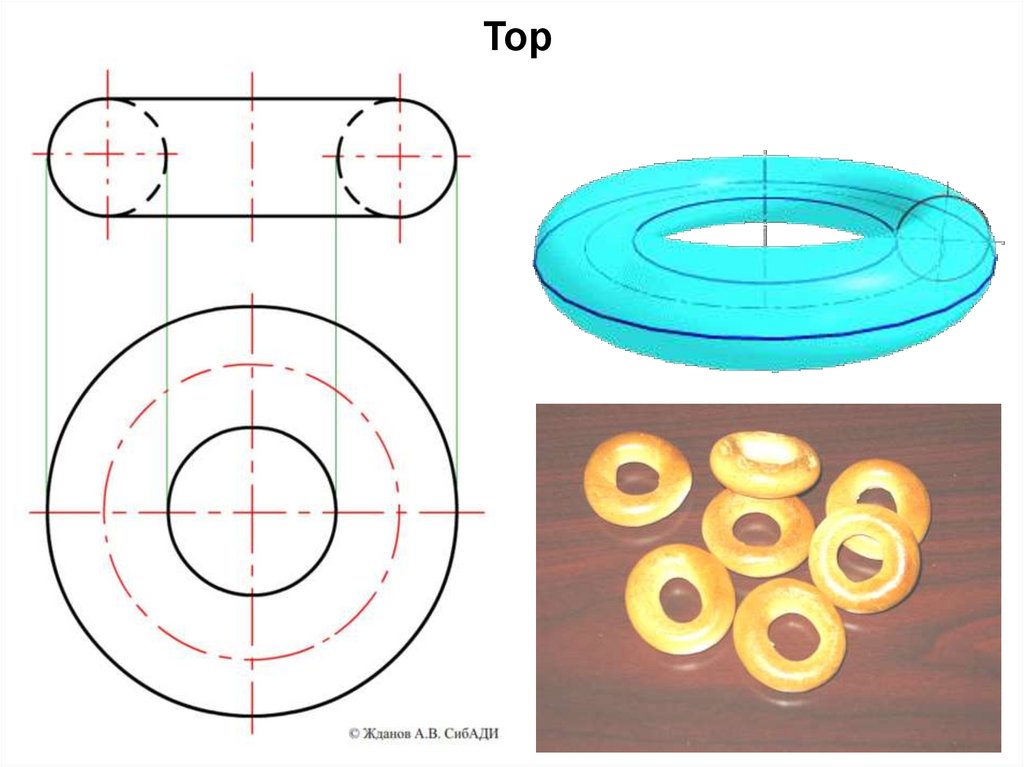
Тор54.
55.
56.
57.
Сфера58.
Эллипсоид сжатый(образуется вращением эллипса вокруг малой оси)
59.
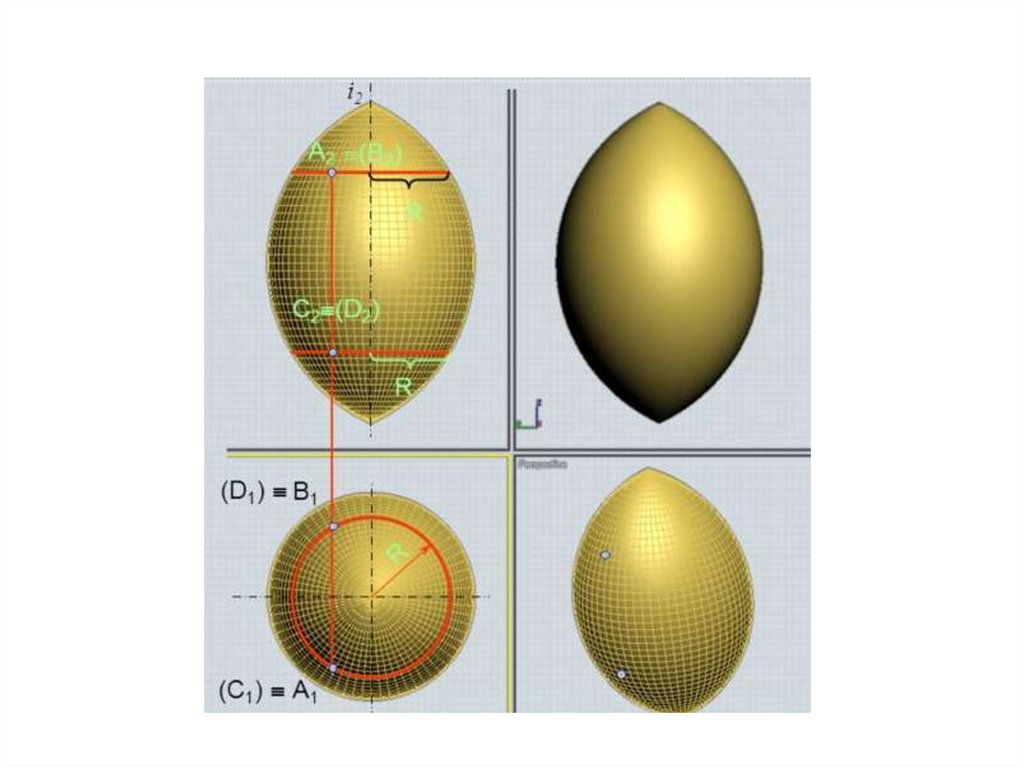
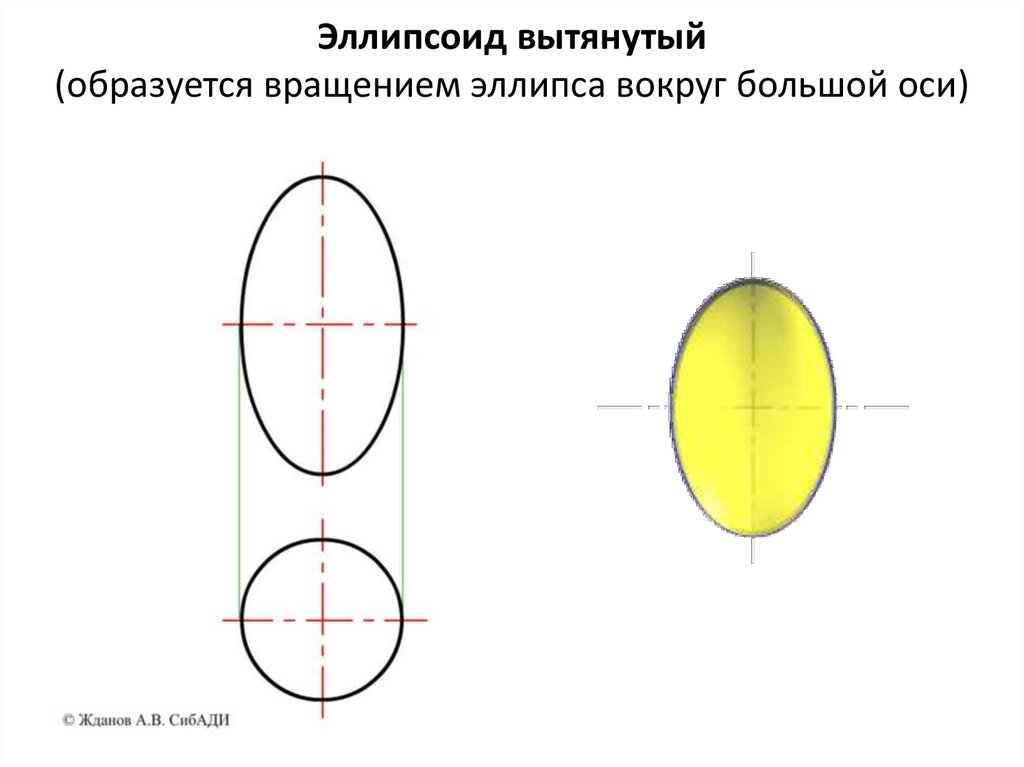
Эллипсоид вытянутый(образуется вращением эллипса вокруг большой оси)
60.
Параболоид вращения61.
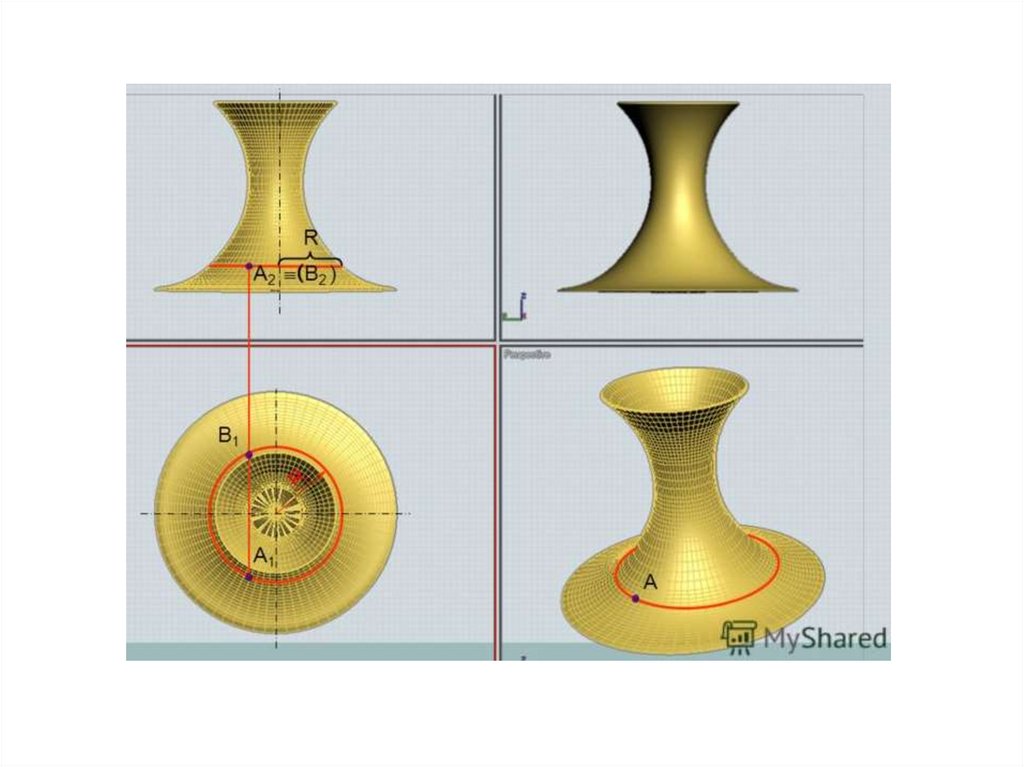
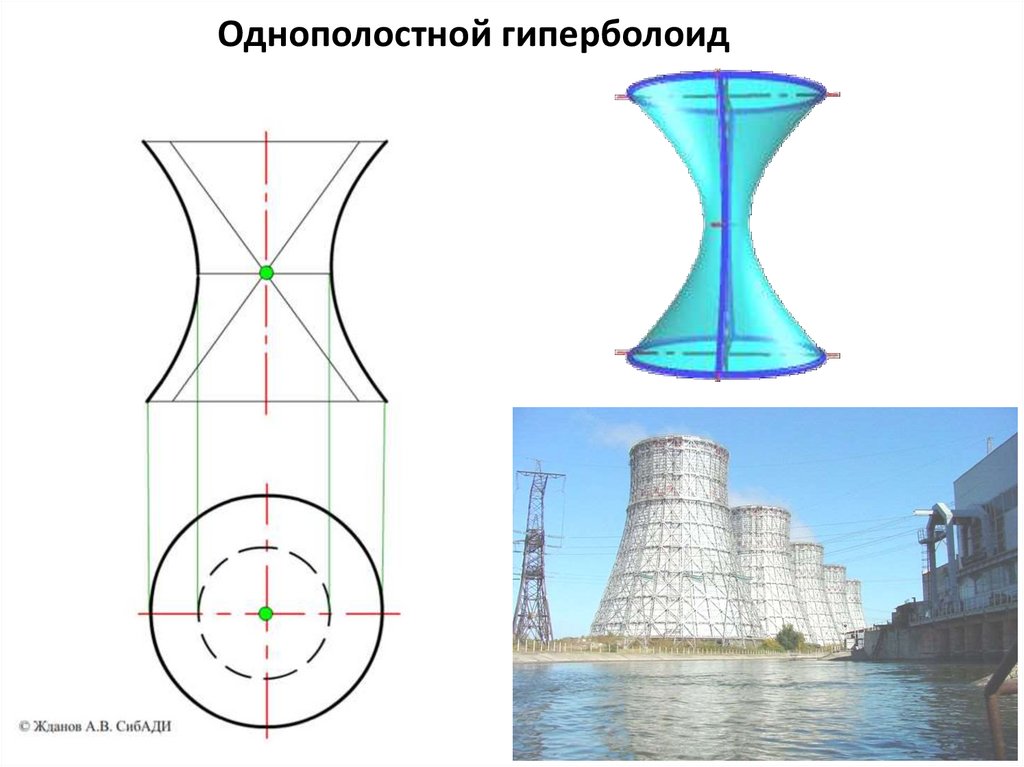
Однополостной гиперболоид62.
Двуполостной гиперболоид63.
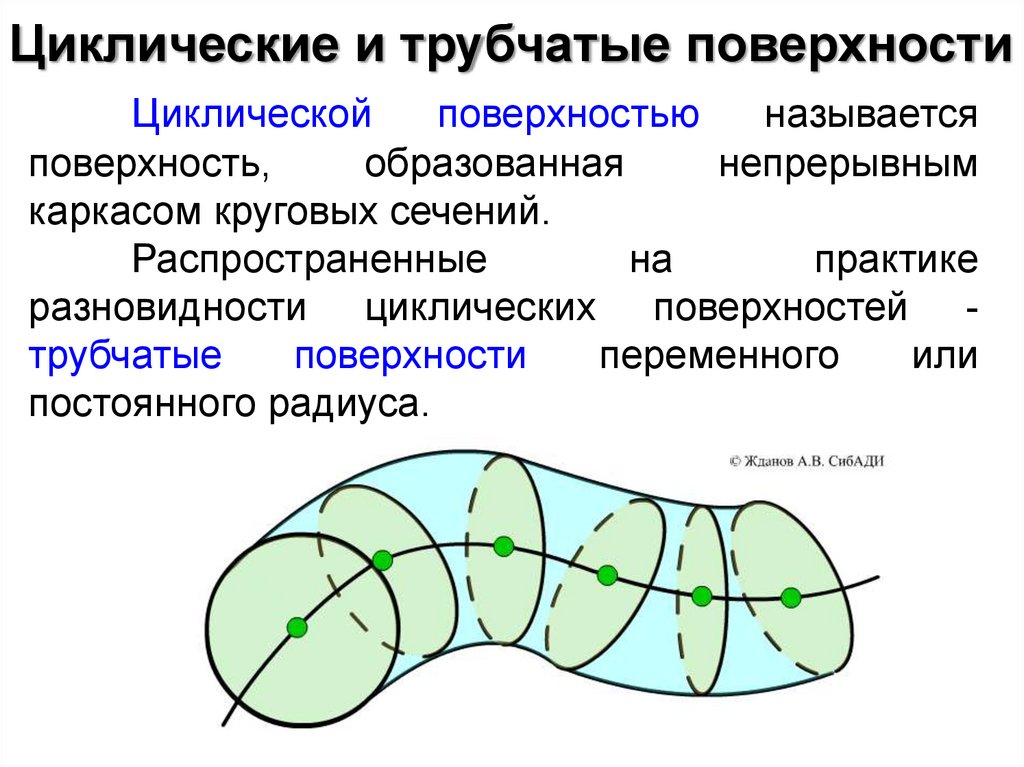
Циклические и трубчатые поверхности64.
Циклические и трубчатые поверхностиЦиклической
поверхностью
называется
поверхность,
образованная
непрерывным
каркасом круговых сечений.
65.
Циклические и трубчатые поверхностиЦиклической
поверхностью
называется
поверхность,
образованная
непрерывным
каркасом круговых сечений.
Распространенные
на
практике
разновидности циклических поверхностей трубчатые
поверхности
переменного
или
постоянного радиуса.
66.
Циклические и трубчатые поверхностиЦиклической
поверхностью
называется
поверхность,
образованная
непрерывным
каркасом круговых сечений.
Распространенные
на
практике
разновидности циклических поверхностей трубчатые
поверхности
переменного
или
постоянного радиуса.
67.
68. Поверхности Каталана
69. Поверхности Каталана
Поверхность Каталана – линейчатаяповерхность,
прямолинейные
образующие
которой параллельны одной и той же плоскости.
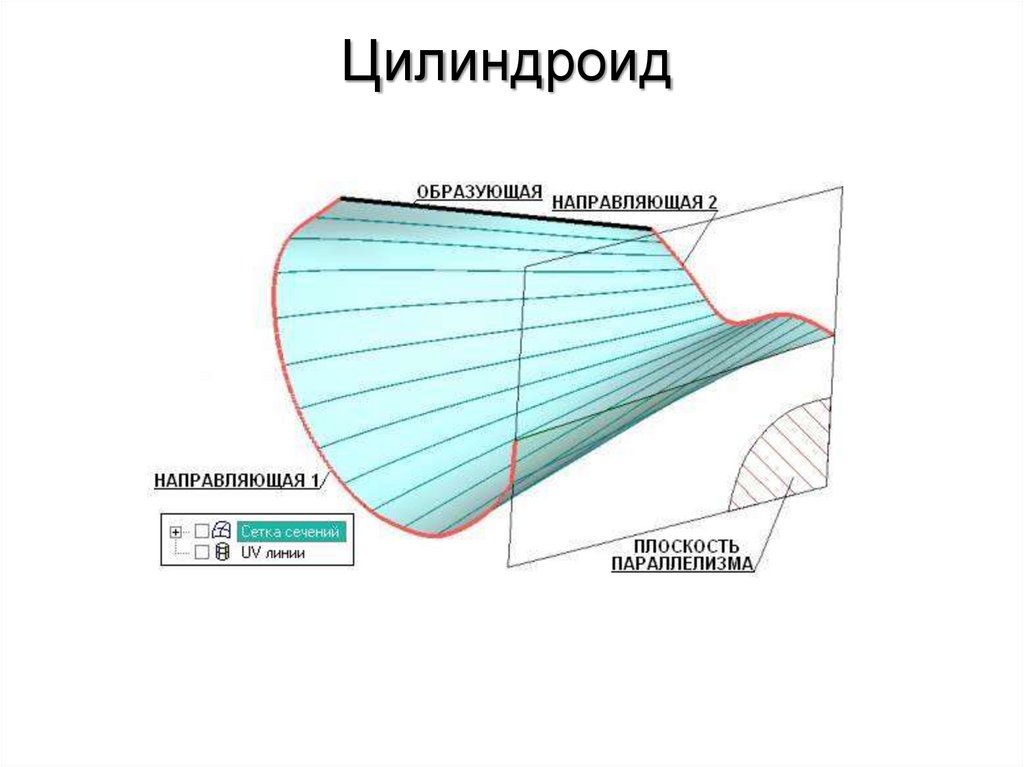
70. Поверхности Каталана
Поверхность Каталана – линейчатаяповерхность,
прямолинейные
образующие
которой параллельны одной и той же плоскости.
Цилиндроидом называется поверхность,
образованная движением прямой линии,
скользящей
по
двум
криволинейным
направляющим, не принадлежащим одной
плоскости, и остающейся во всех своих
положениях параллельной некоторой заданной
плоскости.
Эта
плоскость
называется
плоскостью параллелизма.
71. Цилиндроид
72.
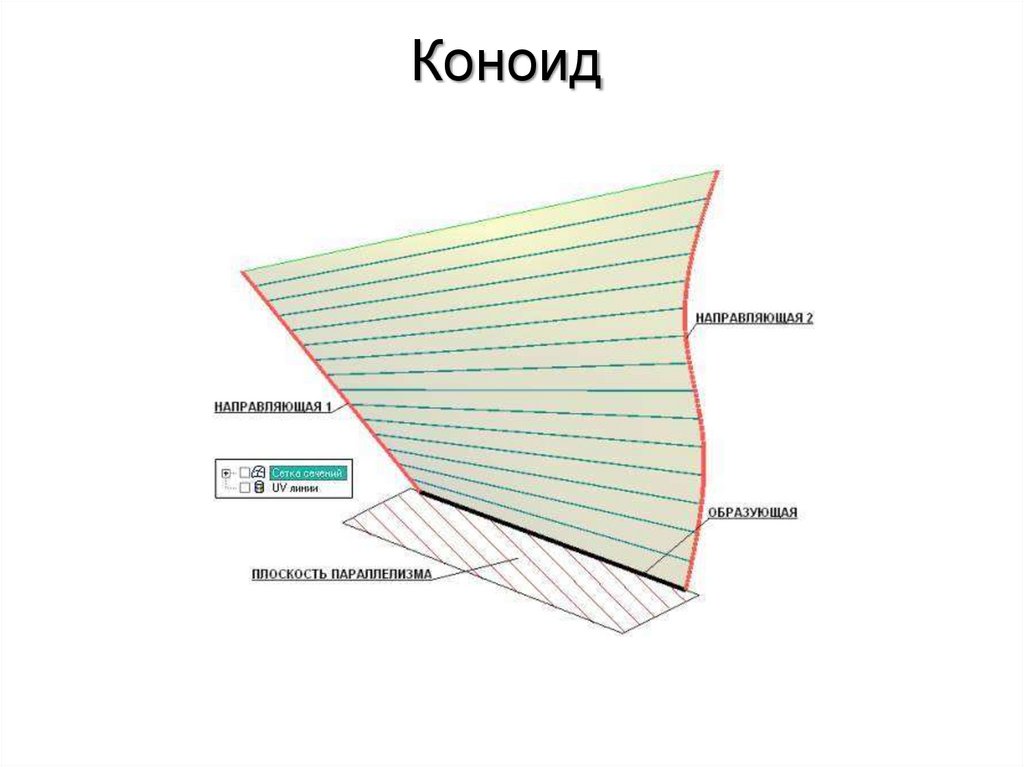
Коноидомназывается
поверхность,
образованная движением прямой линии,
скользящей по двум направляющим, одна из
которых – кривая, а вторая – прямая, и
остающейся во всех своих положениях
параллельной
некоторой
плоскости
параллелизма.
73. Коноид
74.
Коноидомназывается
поверхность,
образованная движением прямой линии,
скользящей по двум направляющим, одна из
которых – кривая, а вторая – прямая, и
остающейся во всех своих положениях
параллельной
некоторой
плоскости
параллелизма.
Косой плоскостью называется поверхность,
образованная движением прямой линии,
скользящей по двум скрещивающимся прямым
и остающейся во всех своих положениях
параллельной
некоторой
плоскости
параллелизма.
75. Косая плоскость
76.
Если в качестве кривойнаправляющей
коноида
взять
цилиндрическую
винтовую линию, в качестве
прямой направляющей –
ось винтовой линии, а за
плоскость параллелизма –
плоскость,
перпендикулярную
оси
винтовой
линии,
то
поверхность, образованная
при
этих
условиях,
называется
винтовым
коноидом
или
прямым
геликоидом.
77.
Если в качестве кривойнаправляющей
коноида
взять
цилиндрическую
винтовую линию, в качестве
прямой направляющей –
ось винтовой линии, а за
плоскость параллелизма –
плоскость,
перпендикулярную
оси
винтовой
линии,
то
поверхность, образованная
при
этих
условиях,
называется
винтовым
коноидом
или
прямым
геликоидом.
78.
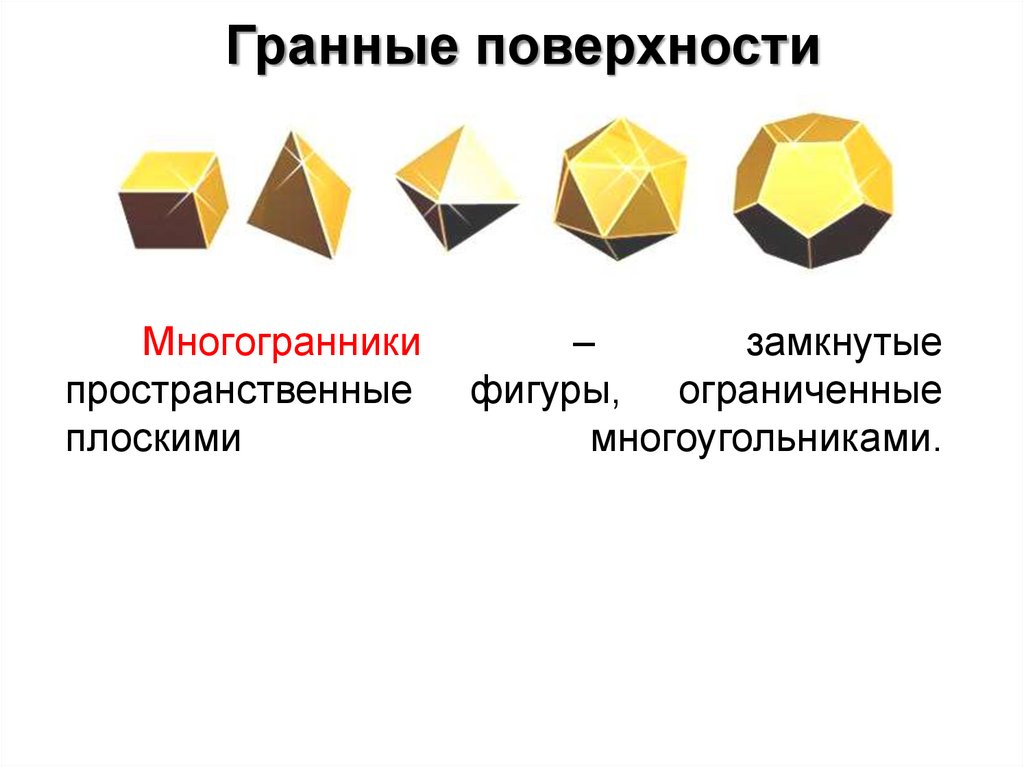
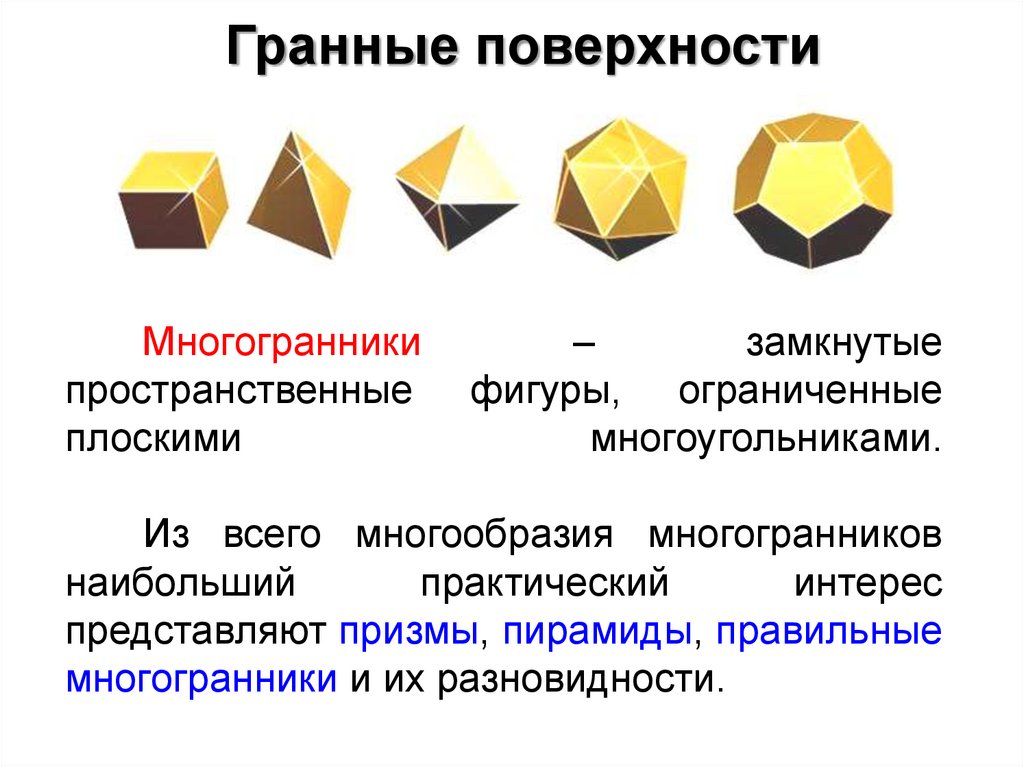
Гранные поверхности79.
Гранные поверхностиМногогранники
пространственные
плоскими
–
замкнутые
фигуры, ограниченные
многоугольниками.
80.
Гранные поверхностиМногогранники
пространственные
плоскими
–
замкнутые
фигуры, ограниченные
многоугольниками.
Из всего многообразия многогранников
наибольший
практический
интерес
представляют призмы, пирамиды, правильные
многогранники и их разновидности.
81.
Элементы гранных поверхностей82.
Элементы гранных поверхностейПирамида
83.
Элементы гранных поверхностейПризма
Пирамида
84.
Нахождение точек на поверхностях85.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
86.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
Точки на поверхностях вращения находят при
помощи параллелей и меридианов.
87.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
Точки на поверхностях вращения находят при
помощи параллелей и меридианов.
То есть на поверхности строят геометрически
простые линии:
88.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
Точки на поверхностях вращения находят при
помощи параллелей и меридианов.
То есть на поверхности строят геометрически
простые линии:
ОКРУЖНОСТИ
89.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
Точки на поверхностях вращения находят при
помощи параллелей и меридианов.
То есть на поверхности строят геометрически
простые линии:
ОКРУЖНОСТИ
или
90.
Нахождение точек на поверхностяхТочка принадлежит поверхности, если она
принадлежит любой линии, принадлежащей этой
поверхности.
Точки на поверхностях вращения находят при
помощи параллелей и меридианов.
То есть на поверхности строят геометрически
простые линии:
ОКРУЖНОСТИ
или
ПРЯМЫЕ
91.
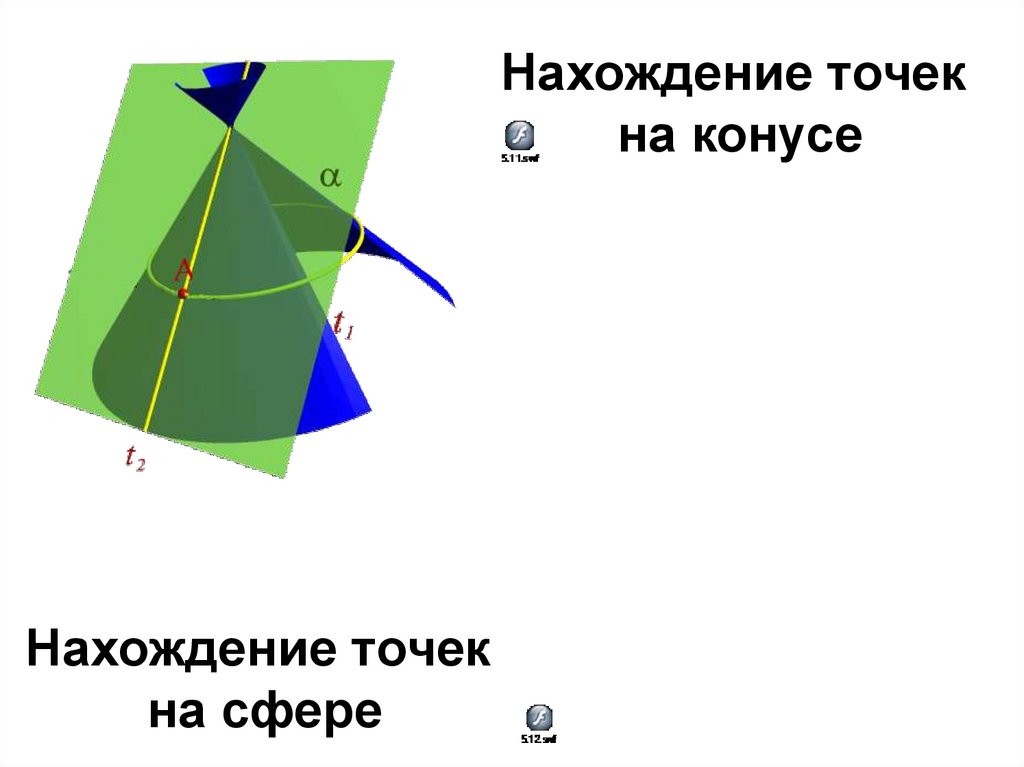
Нахождение точекна конусе
92.
Нахождение точекна конусе
93.
Нахождение точекна конусе
Нахождение точек
на сфере
94.
Нахождение точекна конусе
Нахождение точек
на сфере
95.
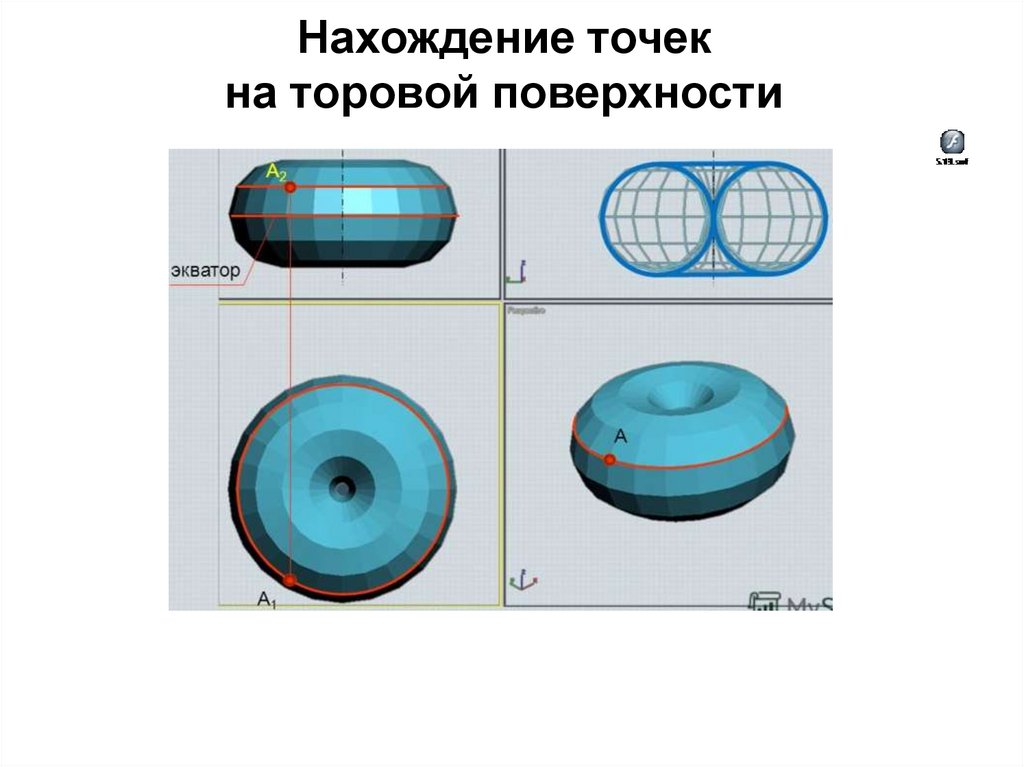
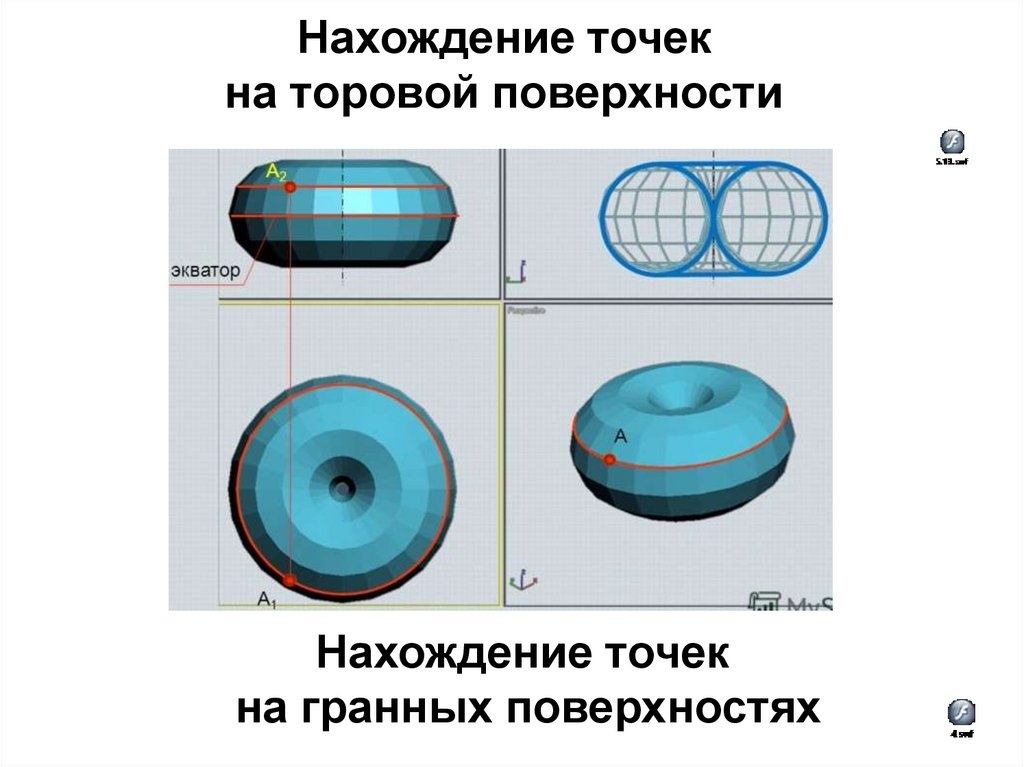
Нахождение точекна торовой поверхности
96.
Нахождение точекна торовой поверхности
97.
Нахождение точекна торовой поверхности
Нахождение точек
на гранных поверхностях













































































 drafting
drafting








