Similar presentations:
Информационные модели на графах
1.
Информационные модели на графах2.
Состав графа• Наглядным средством представления состава и структуры
системы является граф.
• Граф состоит из вершин, связанных линиями.
• Линия, направленная (со стрелкой), называется дугой.
• Линия, ненаправленная (без стрелки) называется ребром.
• Линия, выходящая из некоторой вершины и входящая в нее
же, называется петлей.
3.
Изображение вершин4.
СетиГраф, отражающий отношение «переписываются» между
объектами класса «дети»
Юра
Аня
Маша
Коля
Витя
Граф называется неориентированным, если его вершины
соединены ребрами
5.
СетиЮра
Аня
Маша
Коля
Витя
Путь по вершинам и ребрам графа, включающий любое
ребро графа не более одного раза, называется цепью.
Пример цепи: Юра – Аня – Витя – Коля
6.
СетиЮра
Аня
Маша
Коля
Витя
Цепь, начальная и конечная вершины которой совпадают,
называются циклом.
Пример цикла: Аня – Коля – Витя – Аня
7.
СетиЮра
Аня
Маша
Коля
Витя
Граф называется ориентированным, если его вершины
соединены дугами
8.
Сети182
127
158
Москва, 1147
Владимир, 1108
Переславль Залесский, 1152
Граф называется взвешенным, если его вершины или
ребра (дуги) характеризуются некоторой дополнительной
информацией – весом вершины или ребра (дуги)
9.
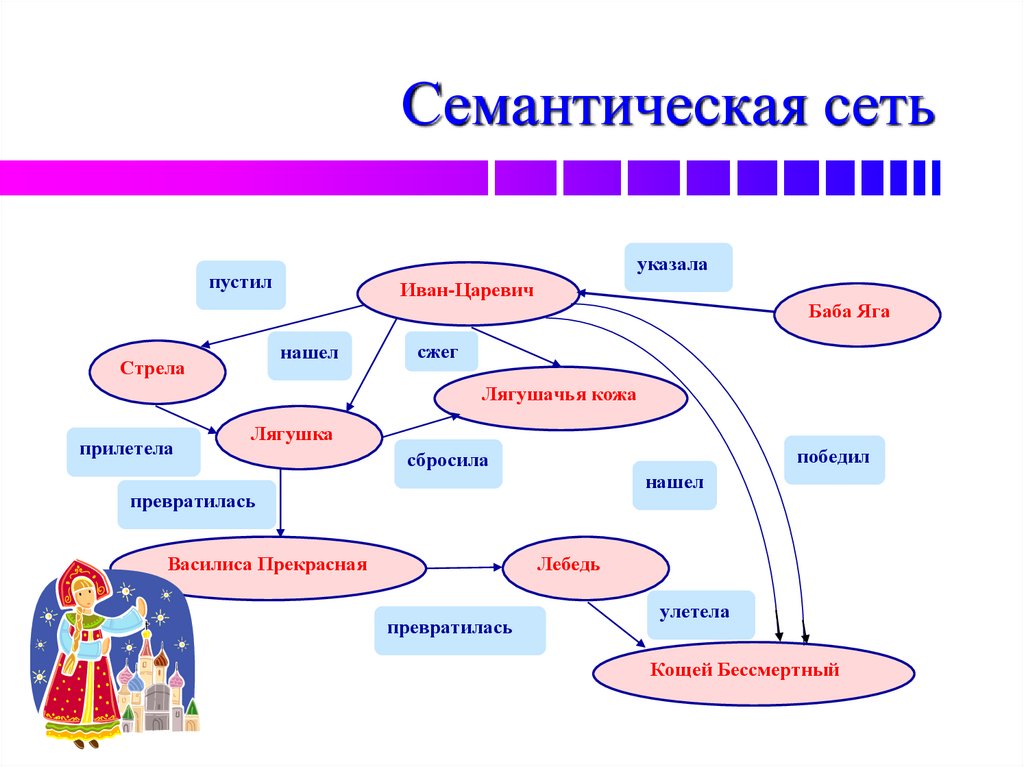
Семантическая сетьуказала
пустил
Иван-Царевич
нашел
Стрела
Баба Яга
сжег
Лягушачья кожа
прилетела
Лягушка
победил
сбросила
нашел
превратилась
Василиса Прекрасная
Лебедь
превратилась
улетела
Кощей Бессмертный
10.
Иерархия - это расположение частей или элементов целого впорядке от высшего к низшему.
Директор
Заместители директора
Учителя
Ученики
Отношения подчиненности в школе
11.
Дерево – граф иерархической структуры.Между любыми двумя его вершинами существует единственный
путь. Дерево не содержит циклов и петель.
компьютер
суперкомпьютер
настольный
рабочая станция
персональный
компьютер
портативный
карманный
Классификация компьютеров
12.
Корень – главная вершина дерева.Предок – объект верхнего уровня.
Потомок – объект нижнего уровня.
Листья – вершины, не имеющие потомков.
?
Укажите перечисленные объекты у дерева
Чемпион
Финалисты
Участники ½ финала
Участники ¼ финала
Первоначальные игроки
Олимпийская система спортивных соревнований
13.
1. Какие из приведенных графов являются деревьями?2. Найдите степени вершин в графе на рисунке 2.
3. На рисунке 3 изображен граф. Назовите один из путей от A до F .
Существует ли путь от A до F проходящий через все вершины графа?
4. Найдите в графе на рисунке 3 циклы, содержащие:
a) 3 ребра;
b) 6 ребер;
5. Найдите несвязные графы .
Рис. 1
Рис. 2
Рис. 3
Рис. 4
Рис. 5
14.
Зачем нужны деревья?Для организации данных
Классификация объектов
Описания структуры
Для решения задач, в которых надо найти
• Все существующие решения
• Самое короткое решение или длинное решение
• Разработать стратегию игры
• И так далее.
15.
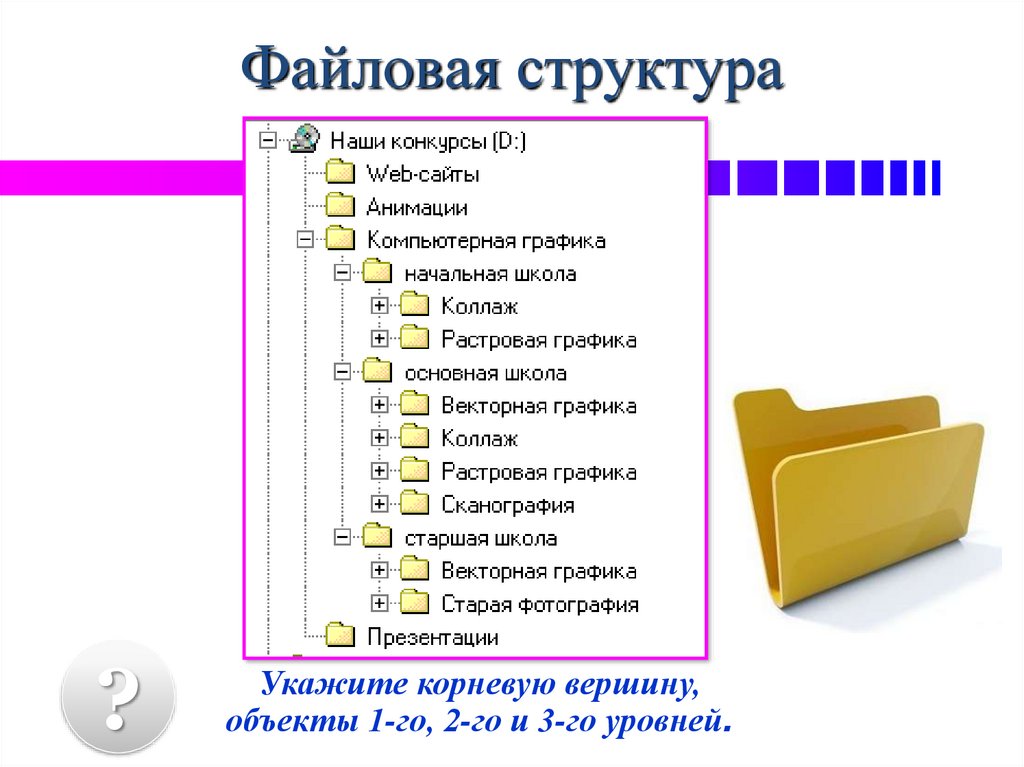
Файловая структура?
Укажите корневую вершину,
объекты 1-го, 2-го и 3-го уровней.
16.
Графы при решении задач?
Сколькими способами можно рассадить
в ряд на три стула трёх учеников?
Выписать все возможные случаи.
Чтобы выписать все случаи,
решение можно представить в виде дерева.
17.
Решение в виде дереваО
А
В
С
С
С
В
А
С
А
В
А
А
В
В
С
Если
на первом
стуле
сидит
А,случае
то на
Выпишем
все
возможные
случаи:
Очевидно,
На первый
что
стултретий
посадим
стуллюбого
вученик
каждом
ученика:
второй стул
можно
посадить
В ученик
или
С. Действуем
А-В-С,
А-С-В,
В-А-С,
В-С-А,
С-А-В,
С-В-А.
займёт
оставшийся
А,В,С
аналогично и для других учеников.
18.
Отыскание пути1
2
3
5
4
7
8
6
9
На рисунке изображена
схема местности.
Передвигаться из пункта в
пункт можно только в
направлении стрелок. В
каждом пункте можно
бывать не более одного раза.
Сколькими способами можно
попасть из пункта 1 в пункт
9? У какого из путей
наименьшая длина? У какого
наибольшая длина?
19.
1Решение задачи
2
3
5
4
6
1
5
4
7
2
8
9
1 ярус
5
7
7
9
5
8
3
2 ярус
9
7
8
8
8
97
9
8
6
3 ярус
8
9
9
9
8
9
9
5
4 ярус
9
9
9
7
8
5 ярус
Кратчайший путь: 1 5 9. Его длинна 2.
8
Длина наиболее продолжительного пути 7: 1 2 3 6 5 7 8 9.
Число путей 14
9
9
6 ярус
7 ярус
20.
МАТРИЦЫ ГРАФОВВ1
В2
7
9
4
В0
11 В4
3 В3
4
2
6
5
5
В6
4
8
В5
.
B0
B1
B2
B3
B4
B5
B6
B0
0
4
0
6
0
5
0
B1
4
0
7
3
0
0
0
B2
0
7
0
0
11
0
9
B3
6
3
0
0
4
5
0
B4
0
0
11
4
0
4
2
B5
5
0
0
5
4
0
8
B6
0
0
9
0
2
8
0
21.
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересеченияхстрок и столбцов таблиц, означают стоимость проезда между соответствующими соседними
станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “Минимальная стоимость проезда
из А в B не больше 6”.
Стоимость проезда по маршруту складывается из стоимостей проезда между
соответствующими соседними станциями.
2)
1)
A
B C
A
3
B
4
C
3
D
1
Е
C
D
Е
A
3
1
1
2
B
4
2
C
3
D
1
Е
1
D Е
A
1
4
2
2
A
B
2
4
C
2
1
D
B
4
C
D Е
A
3
1
B
4
C
3
D
1
Е
2
1
2
D
4
1
B
2
C
C
4
4
1
2
1
4
2
4
1
2
A
B
B
1
1
4
C
D Е
1
Е
1
1
B
A
2
3
E
A
D
1
3
4
C
B
A
B
1
E
4)
A
2
A
3
E
3)
E
4
C
2
4
D
D
AC C B - 7
AC C B - 7
AC C B - 7
AD DC CB - 9
AC CE EB - 7
AE EC CB - 7
AC CE EB - 6
AD DC CE EB - 8
22.
Два игрока играют в следующую игру. Перед ними лежат две кучки камней, впервой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно много
камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3
раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу.
Выигрывает игрок, после хода которого общее число камней в двух кучах
становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок,
делающий первый ход, или игрок, делающий второй ход? Каким должен быть
первый ход выигрывающего игрока? Ответ обоснуйте.
3,2, ∑ 5
9,2, ∑ 11
27,2, ∑ 29
3,6, ∑ 9
3,18, ∑ 21 12,2, ∑ 14
12,3, ∑ 15
3,3, ∑ 6
4,2, ∑ 6
4,3, ∑ 7
4,9, ∑ 13
5,2, ∑ 7
5,3, ∑ 8
1 ход
1 игрок
4,6, ∑ 10
4,4, ∑ 8
36,3,∑39 12,9,∑21 12,4,∑16 13,3,∑16 4,27,∑31 12,9,∑21
3,4,∑∑12
7
3,9,
2 ход
2 игрок
3 ход
1 игрок
4 ход
15,3,∑18 12,4,∑16
2 игрок




















 informatics
informatics








