Similar presentations:
Системы счисления
1.
Системы счисленияВашему вниманию представлены теоретический материал, примеры решения задач и
упражнения для тренировки по теме «Системы счисления». Некоторые упражнения и
рассуждения в тексте основываются на результатах выполнения предыдущих упражнений.
Поэтому для лучшего понимания и закрепления материала рекомендуется при прочтении
текста выполнять задания сразу.
Цифра – это письменный знак, изображающий число. Система счисления – это способ
записи чисел и сопоставления этим записям реальных значений.
В древнейшие времена числа обозначались прямолинейными пометками «палочками»:
одна палочка изображала единицу, две – двойку, … . Для изображения больших чисел этот
способ неудобен. Поэтому с течением времени были созданы знаки для бóльших чисел. У
некоторых народов (древнегреческая, славянская, армянская и древнегрузинская нумерация)
для изображения чисел использовались буквы алфавита. Для отличия цифр от букв над
цифрами писали черточки (у славян - «титло»):
= 1,
= 40,
= 200. Этот способ до сих
пор сохранился в римских цифрах.
В позднейшем своем виде римские цифры1 выглядят так:
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.
Все целые числа записываются с помощью повторения этих цифр. При этом, если бóльшая
цифра стоит перед меньшей, то они складываются; если меньшая цифра стоит перед
большей (в этом случае она не может повторяться), то меньшая вычитается из большей.
Одна и та же цифра ставится подряд не более трех раз.
Примеры:
2002 = M M I I, 1999 = M C M X C I X, 300 = C C C, 400 = C D.
Арифметические действия с такими числами производить очень неудобно, поэтому
римские цифры используются для нумерации томов, разделов и глав книг, обозначения
номера века или тысячелетия (XIX век, II тысячелетие до н. э.), порядкового номера монарха
(Карл V, Екатерина II) и т. п.
Системы счисления, устроенные таким образом, называют аддитивными.
Упражнение 1
А) Запишите в десятичной системе счисления числа XCI, XXIII, CDLXXII, MCMXIX.
Б) Запишите римскими цифрами числа 17, 48, 293, 965, 2010.
1
Подробнее о римских цифрах можно прочесть по ссылке http://ru.wikipedia.org/wiki/Римские_цифры
2.
В Древнем Вавилоне примерно за 40 веков до нашего времени создалась поместная(позиционная) нумерация, то есть такой способ изображения чисел, при котором одна и та
же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой.
Например, в числе 52 цифра 5 обозначает пять десятков: 50 = 5⋅10, а в числе 578 та же цифра
обозначает пять сотен: 500 = 5⋅102. Позиции, в которых располагаются цифры, называют
разрядами. Единица каждого разряда в десятичной системе имеет своё название: единицы,
десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллион и т.д., десятые, сотые,
тысячные, десятитысячные и т. д.
В недесятичной позиционной системе счисления для представления чисел выбираются
некоторые символы (цифры), а остальные числа получаются в результате каких-либо
операций над цифрами данной системы счисления. Количество цифр, используемых для
записи чисел, называется основанием системы счисления (это натуральное число). Заметим,
что основание системы счисления равно числу единиц какого-либо разряда, объединяемых в
единицу более старшего разряда. Цифры в системе с основанием b > 0 принимают значения
от нуля до b – 1. Например, в десятичной системе счисления десять цифр: 0, 1, 2, …, 9; в
системе с основанием 2 имеем две цифры – ноль и единица, в системе с основанием 8 –
цифры: 0, 1, 2, 3, 4, 5, 6, 7. Если основание больше 10, то для обозначения цифр могут
использоваться буквы латинского алфавита.
Например, в шестнадцатеричной системе счисления:
Цифры в 16-ричной системе
0 1 2 3 4 5 6 7 8 9 A
B
C
D
E
F
Значения в десятичной системе 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Для того, чтобы указать, в какой системе счисления записано число, основание
системы счисления пишут в качестве нижнего индекса рядом с числом. Поскольку чаще
всего мы работаем с десятичной системой счисления, то основание 10 не пишем.
Упражнение 2
Выпишите цифры в тринадцатеричной системе счисления и их значения в десятичной
системе счисления
Любое число в позиционной системе счисления можно представить в виде суммы,
каждое слагаемое которой равно произведению цифры на единицу соответствующего ей
разряда. При этом единицу каждого разряда можно записать в виде степени какого-либо
числа. Мы привыкли к десятичной системе счисления, в ней числа представляются в виде:
3.
α n α n −1 ... α 2 α 1 α 0 , α −1 ...α − k =k
=αn·10n + αn–1·10n–1 + … + α2·102 + α1·10 + α0 + α −1·10−1 + …+ α −k·10− ,
где αn, αn–1, …, α2, α1, α0, α −1, …, α −k – цифры данного числа: α0 – число единиц, α1 –
число десятков, α2 – число сотен и т. д. Черта над записью (при буквенной записи)
используется для того, чтобы отличать записанные подряд цифры числа от произведения
переменных.
Например, разложение по степеням десяти имеет вид:
2390847,516 = 2·106 + 3·105 + 9·104 + 0·103 + 8·102 + 4·10 + 7·100 + 5·10-1 + 1·10-2 + 6·10-3
Аналогично в системе счисления с основанием b число будет представлено в виде:
α n α n −1 ... α 2 α 1 α 0 , α −1 ...α − k =
k
= αn·bn + αn–1·bn–1 + … + α2·b2 + α1·b1 + α0·b0 + α −1·b−1 + …+ α −k· b − .
Например, разложение числа в восьмеричной системе записывается по степеням числа 8:
4273,518 = 4·83 + 2·82 + 7·8 + 3·80 + 5·8-1 + 1·8-2
Упражнение 3
Запишите числа в виде разложения по степеням основания системы счисления:
А) 101001110,01012; 2548; 2D716
Перевод чисел из системы с основанием b в десятичную
Правило 1. При переводе чисел из системы счисления с основанием b в десятичную систему
счисления необходимо пронумеровать разряды целой части справа налево, начиная с
нулевого, и в дробной части, начиная с разряда сразу после запятой слева направо
(начальный номер -1). Затем вычислить сумму произведений соответствующих значений
разрядов на основание системы счисления в степени, равной номеру разряда.
Например, переведём в десятичную систему двоичное число
5 4 3 2 1 0 −1 −2 −3
110101, 0 1 1 2 = 1 ⋅ 2 5 + 1 ⋅ 2 4 + 0 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 21 + 1 ⋅ 2 0 + 0 ⋅ 2 −1 + 1 ⋅ 2 − 2 + 1 ⋅ 2 −3 =
1 1
3
= 32 + 16 + 4 + 1 + + = 53 = 53,375
4 8
8
Переведём в десятичную систему шестнадцатеричное число
4.
2 1 0 −1 −26 А 9, С 1 16 = 616 ⋅ 16 2 + А16 ⋅ 161 + 916 ⋅ 16 0 + С16 ⋅ 16 −1 + 116 ⋅ 16 − 2 =
= 6 ⋅ 16 2 + 10 ⋅ 161 + 9 ⋅ 16 0 + 12 ⋅ 16 −1 + 1 ⋅ 16 − 2 =
12
1
193
= 1536 + 160 + 9 + +
= 1705
= 1705,75390625
16 256
256
Упражнение 4
Переведите в десятичную систему числа 101001110,01012; 2548; 2D716
Перевод целых чисел из десятичной системы в систему с основанием b
Правило 2. Для перевода целого числа в систему с основанием b нужно разделить это число
на b и запомнить остаток от деления. Полученное частное вновь делится на b, а остаток
запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю.
Остатки от деления на b выписываются в порядке, обратном их получению.
Поясним алгоритм перевода на примере перевода десятичного числа 20 в двоичную
систему. Разделим число 20 на 2 столбиком. Деление будем производить до тех пор, пока
целая часть от деления не станет равной нулю.
Если внимательно посмотреть на процесс деления:
20 = 2·10 + 0 = 2·(2·5 + 0) + 0 = 2·(2·[2·2 +1]+ 0) + 0 = 2·(2·[2·{2·1+0} +1]+ 0) + 0 =
2·(2·[2·{2·(2·0 + 1)+0} +1] + 0) + 0 = 25·0 + 24·1 + 23·0 + 22·1 + 2·0 + 0 = 101002 ,
то можно заметить, что остатки от деления образуют последовательность 00101 – т. е. число
10100, записанное в обратном порядке. Таким образом, чтобы записать число в двоичной
системе, нужно записать остатки, получающиеся в процессе деления, только в обратном
порядке. Аналогично поступают и в случае системы с другим основанием.
20 = 81·2 + 80·4 = 248
20 = 161·1 + 160·4 = 1416
5.
Упражнение 5Переведите
десятичное
число
973
в
двоичную,
четверичную,
восьмеричную
и
шестнадцатеричную системы
Перевод чисел, меньших единицы, из десятичной системы в систему с основанием b
Правило 3. Для перевода числа, меньшего единицы, из десятичной системы в систему с
основанием b нужно:
1) умножить дробную часть числа на b, после чего целая часть запоминается;
2) отбросить целую часть числа после умножения; если дробная часть равна нулю, то
перейти к шагу 3), иначе – к шагу 1)
3) выписать целые части после запятой в порядке их получения.
Примеры:
1. 0,09375 переводим в двоичную систему:
0,09375 ⋅ 2 = 0,1875; 0,1875 ⋅ 2 = 0,375; 0,375 ⋅ 2 = 0,75; 0,75 ⋅ 2 = 1,5; 0,5 ⋅ 2 = 1,0.
Получаем ответ: 0,0937510 = 0,000112.
2. 0,0732421875 переводим в 16-ричную систему:
0,0732421875 ⋅ 16 = 1,171875; 0,171875 ⋅ 16 = 2,75;
0,75 ⋅ 16 = 12 (в 16-ричной системе это значение шестнадцатеричной цифры C).
Получаем ответ: 0, 073242187510 = 0,12С16.
3. Переведём число 0,3125 в двоичную, четверичную, восьмеричную и шестнадцатеричную
системы. Заметим, что для сокращения записи процесс умножения удобно записывать в
виде следующей схемы:
Умножение производится для числа, стоящего справа от вертикальной черты (то есть с
отброшенной целой частью), а целая часть, получающаяся в результате умножения,
записывается слева от вертикальной черты и представляет собой очередную цифру числа
в новой системе счисления.
0,3125 = 0,01012 = 0,114 = 0,248 = 0,516
6.
Заметим, что результатом может быть как конечная, так и бесконечная (возможно,периодическая) дробь в системе счисления с основанием b. Если период выделить не
удается, то приходится обрывать умножение на каком-либо шаге и довольствоваться
приближенной записью исходного числа в системе с основанием b.
Пример 4.
Переведем в двоичную, восьмеричную и шестнадцатеричную системы число 0,26.
Заметим, что в дробной части каждый раз получается новое число, и процесс
умножения может продолжаться довольно долго. Поэтому мы обрываем процесс умножения
на некотором шаге и получаем приближённые значения: 0,26 ≈ 0,01000012, 0,26 ≈ 0,205078.
В процессе умножения на 16 замечаем, что после умножения 0,76 на 16 получили 12,16,
а после отбрасывания целой части нужно будет на 16 умножать число 0,16, которое мы уже
умножали выше. Значит, далее процесс умножения будет повторять уже пройденные шаги,
то есть мы имеем бесконечную периодическую дробь. При записи ответа десятичные
значения 15 и 12 заменяем на шестнадцатеричные цифры F и C. В результате получаем
0,26 = 0,4(28F5C)16.
Упражнение 6
Переведите десятичное число 0,8125 в двоичную, четверичную, восьмеричную и
шестнадцатеричную системы.
Упражнение 7
Переведите
десятичное
число 0,92
в
двоичную,
четверичную,
шестнадцатеричную системы (получить пять знаков после запятой).
восьмеричную
и
7.
Перевод чисел с целой и дробной частьюиз десятичной системы в систему с основанием b
Правило 4. Для перевода числа с целой и дробной частью из десятичной системы в систему с
основанием b нужно перевести отдельно целую часть по правилу 2 и отдельно дробную
часть по правилу 3, а результаты сложить.
Например, переведём число 20,3125 в двоичную систему. Выше мы уже перевели отдельно
целую 20 = 101002 и дробную часть 0,3125 = 0,01012. Следовательно, 20,3125 = 10100,01012.
Упражнение 8
Переведите десятичное число 813,6875 в двоичную, четверичную, восьмеричную и
шестнадцатеричную системы.
Арифметические действия в недесятичных позиционных системах счисления
Арифметические действия над числами в любой позиционной системе счисления
производятся по тем же правилам, что и в десятичной системе. При этом нужно только
пользоваться теми таблицами сложения и умножения, которые соответствуют данному
основанию b системы счисления.
Например, таблицы сложения и умножения в двоичной системе имеют вид:
Таблица сложения
Таблица умножения
+ 0 1
0 0 1
1 1 10
× 0 1
0 0 0
1 0 1
Поясним, как получается 12+12=102. Напомним, что основание системы счисления
равно числу единиц какого-либо разряда, объединяемых в единицу более старшего разряда.
В нашем случае мы складываем как раз количество единиц, равное основанию системы
счисления, значит, получаем единицу следующего разряда, которая записывается как 102.
Составим таблицы сложения и умножения в четверичной системе:
Таблица сложения
+
0
1
2
3
0 1 2 3
0 1 2 3
1 2 3 10
2 3 10 11
3 10 11 12
Поясним, как заполняются эти таблицы.
Таблица умножения
×
0
1
2
3
0
0
0
0
0
1 2 3
0 0 0
1 2 3
2 10 12
3 12 21
8.
Прибавление нуля к некоторому числу всегда дает это число. Прибавление единицы кчислу x равносильно переходу к числу, следующему за x. За единицей в четверичной
системе следует число 24, затем 34, а добавление к последнему ещё одной единицы дает
четыре единицы, которые в системе с основанием 4 объединяются в единицу следующего
разряда, то есть 104. Заметим, что прибавление двойки равносильно прибавлению единицы, а
затем ещё одной единицы, то есть третья строка таблицы сложения получается
прибавлением единицы к числам в предыдущей строке. Аналогично четвертая строка
получается прибавлением единицы к числам из предыдущей строки.
Умножение на ноль всегда дает ноль, а умножение числа на единицу дает само это
число. Умножение числа x на два означает, что нужно прибавить это число к самому себе,
поэтому третья строка (и третий столбец) таблицы умножения совпадает с диагональю
таблицы сложения. Заметим, что осталось заполнить всего одну ячейку таблицы – результат
умножения 34 на 34. Умножение числа x на три равносильно тому, что к результату
умножения на два нужно прибавить x. Согласно таблице умножения 34×24=124.
Следовательно, нам нужно к 124 прибавить 34. По таблице сложения 24+34=114, откуда
124+34=104+24+34=104+114=214.
Упражнение 9
Составьте таблицы сложения и умножения для семеричной системы.
Сложим два числа в двоичной системе. Запишем их столбиком друг под
другом, и будем складывать по отдельности числа в каждом разряде, начиная с
правого. В крайнем правом разряде складываем две единицы, получаем 102, ноль
пишем в соответствующем разряде, а единица переносится в следующий разряд, что на
рисунке отмечено точкой над вторым разрядом справа. Аналогично рассуждаем в
следующих разрядах. В последнем (крайнем левом) разряде мы складываем две единицы и
получаем 102, но поскольку произошёл перенос из соседнего разряда, то добавляем ещё
единицу и получаем 112, то есть записываем единицу в соответствующий разряд и единицу
переносим в следующий. Таким образом, 1101012 + 1011012 = 11000102. Для проверки
переведём слагаемые и результат в десятичную систему: 53 + 45 = 98.
9.
Аналогично производится умножение: 11012 · 10112 = 100011112, проверка: 13 · 11 = 14.Аналогично выполняются действия в системах с другим основанием.
Например, сложим два семеричных числа 5057 и 347. Запишем числа в столбик и
будем проводить сложение поразрядно. В младшем разряде нам нужно сложить 57
и 47. Если мы добавим 27 к 57, то получим единицу следующего разряда, то есть 107.
Складывая 47 и 57, мы добавляем ещё 27 к 107 и получаем 127. Пишем две единицы в
младший разряд результата, а единица переносится в следующий разряд. В следующем
разряде нужно прибавить запомненную единицу к 37, а в последнем разряде остаётся
переписать 57.
Рассмотрим теперь пример умножения семеричных чисел 2367 и 27. По
таблице умножения в семеричной системе 67×27=157, пять пишем в последний
разряд результата, а единицу переносим в следующий разряд. Далее 37×27=67, и
прибавляем единицу, перенесённую из младшего разряда, получаем 107, то есть ноль пишем,
а единицу переносим в соседний разряд. Наконец, 27×27=47, и прибавляем единицу,
перенесённую из предыдущего разряда, получаем 57. Таким образом, 2367×27=5057.
5
0 1,
2, 3
4
6
42
0
+1
6
+3
33
4
2
1
2
3
21
0
3
+1
15
правому краю. Если числа содержат дробную часть, то
5
умножение ведём, не обращая внимания на запятые, а в
×
+4
2
1
0
4
13
0
2
+1
11
3
0
3
1
5
5
5
+1
6
+1
+1
1
7
7
Поясним процесс умножения многозначных чисел.
Как и в десятичной системе при умножении в столбик
числа записываем друг под другом, выравнивая по
результате запятой отделим столько разрядов, сколько
10
составляют в сумме количества разрядов после запятой в
3
1 5 5 6, 0 0 3
7
множителях.
Для наглядности промежуточные результаты будем записывать подробно. Перемножим
числа 501,47 и 2,367. По таблице умножения в семеричной системе 47×67=337, 17×67=67,
07×67=07, 57×67=427. Эти числа записаны мелким синим шрифтом в первой строке после
черты, отделяющей сомножители от промежуточных вычислений. Теперь записываем
10.
результат умножения на 67. Заметим, что в последнем разряде получилось двузначное число,значит, младший разряд этого числа будет записан в этом же разряде, а старший даст
перенос в следующий разряд. Отметим это во второй строке (также мелким синим шрифтом)
как «+3» в том разряде, куда произошёл перенос. Во втором разряде справа 67 + 37 =127, то
есть две единицы в текущем разряде и одну единицу переносим в следующий разряд. В
следующем разряде 07 + 17 = 17, и в последнем разряде два пишем, а 4 переносим в
следующий разряд. Итак, получили результат умножения на цифру 6: 421237. Аналогично
рассуждаем при умножении на другие цифры второго сомножителя. Осталось сложить
результаты умножения на отдельные цифры. В последнем разряде имеем только число 3, во
втором разряде справа 27 + 57 = 107, значит, ноль пишем в этом разряде а единицу переносим
в следующий (отмечая это как «+1» в третьем столбце справа). В третьем справа разряде
17+47+17=67, что отмечено в верхней строке результата, да ещё нужно прибавить единицу,
перешедшую из предыдущего разряда, то есть снова имеем 107. Далее (27+07+37)+17=67 и в
следующий разряд ничего переносить не надо. В следующих столбиках 47+17+07=57, 27+37=57
и единица в крайнем левом разряде. В первом сомножителе была одна цифра после запятой,
во втором – две, значит, в результате будет 1+2=3 цифры после запятой. Итак, получили
501,47 × 2,367 = 1556,0037.
Упражнение 10
Выполните действия:
А) 10001111102 + 10110001012 ; 620,28 + 1453,38 ; 348,116 + 2D4,416.
Б) 11001102×1100102 ; 177,48 × 23,48; в) 10,616 × 2A,816 .
В*) 11000010102 – 100000112 ; 1520,58 – 403,28; 368,A16 – 239,D16.
Г*) 1001110002 : 11012 ; 43438 : 318; A3B16 : 1B16 .
Перевод чисел из системы с основанием s в систему с основанием r
Для перевода числа из системы с основанием s в систему с основанием r требуется
записать число в виде суммы
∑α s
i
i
, где цифры αi и s выражены в новой r-системе, и
i
выполнить соответствующие арифметические действия по правилам r-системы.
Например, переведем число 21045 в семеричную систему счисления. Заметим, что
промежуточные действия нами выполнены выше.
21045 = 27⋅ 537 +17⋅ 5 72 +07⋅ 517 +47⋅ 5 07 =27⋅2367+17⋅347 +47 =5057+347 +47 =5467
11.
Поскольку выполнение действий в системе счисления с основанием, отличным от 10,производить затруднительно, то обычно используют следующее правило:
Правило 5. Для перевода числа из одной системы в другую используют десятичную систему
в качестве промежуточной (переводят число сначала из системы с основанием s в
десятичную систему по правилу 1, а потом из десятичной – в систему с основанием r по
правилу 4). Если основания старой и новой систем счисления являются степенями числа 2,
то в качестве промежуточной используют двоичную систему (правила 6 и 7).
Поясним это правило на числе 21045 из рассмотренного выше примера. Переведем это
число сначала в десятичную систему:
21045 = 2⋅53+1⋅52+0⋅5+4⋅50 = 2⋅125 + 1⋅25 + 4 = 279
Теперь переведем это число из десятичной системы в семеричную, получим 279 = 5467.
Таким образом, 21045 = 279 = 5467. Получили тот же самый результат, что и выше.
Упражнение 11
Переведите :
А) число 1002123 в пятеричную и семеричную системы,
Б) число 20145 в троичную и семеричную системы,
В) число 5467 в троичную и пятеричную системы.
Перевод чисел из системы с основанием 2m в систему с основанием 2n
В системах, основаниями которых являются степени числа 2, процесс перевода
упрощается, если в качестве промежуточной системы используется двоичная. Прежде, чем
сформулировать правила перевода чисел, составим таблицу, в которой выпишем
представление чисел от нуля до 16 в системах, основаниями которых являются степени
двойки. Эту таблицу рекомендуем выучить.
12.
основание4
0
0
1
1
10
2
11
3
100
10
101
11
110
12
111
13
1000
20
1001
21
1010
22
1011
23
1100
30
1101
31
1110
32
1111
33
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
16
10000
100
8
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
20
10
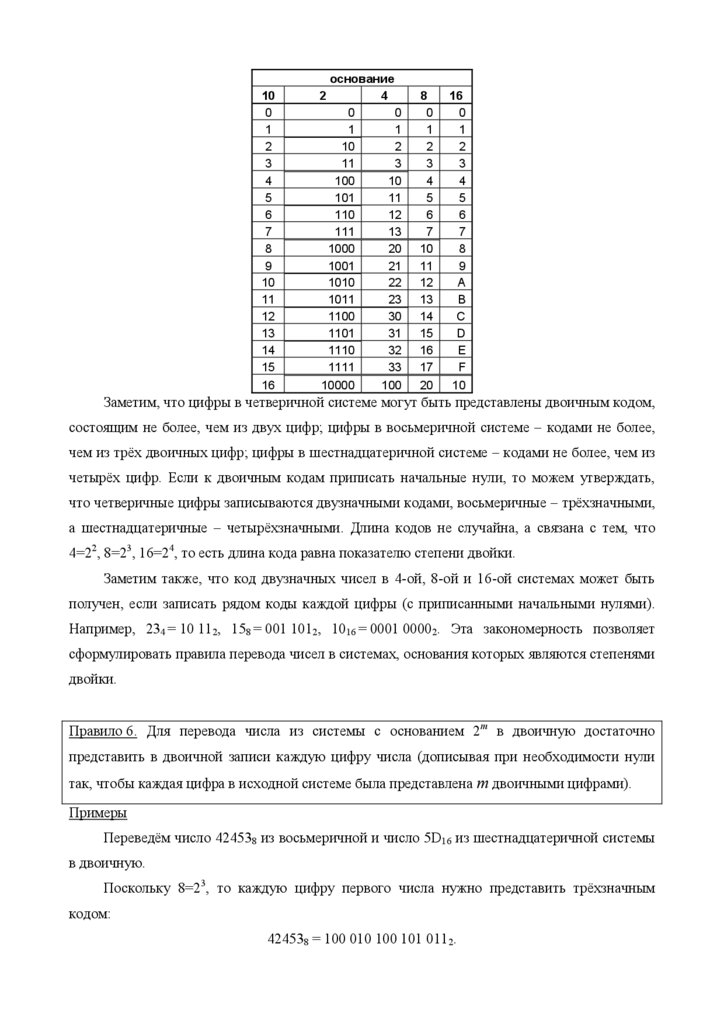
Заметим, что цифры в четверичной системе могут быть представлены двоичным кодом,
состоящим не более, чем из двух цифр; цифры в восьмеричной системе – кодами не более,
чем из трёх двоичных цифр; цифры в шестнадцатеричной системе – кодами не более, чем из
четырёх цифр. Если к двоичным кодам приписать начальные нули, то можем утверждать,
что четверичные цифры записываются двузначными кодами, восьмеричные – трёхзначными,
а шестнадцатеричные – четырёхзначными. Длина кодов не случайна, а связана с тем, что
4=22, 8=23, 16=24, то есть длина кода равна показателю степени двойки.
Заметим также, что код двузначных чисел в 4-ой, 8-ой и 16-ой системах может быть
получен, если записать рядом коды каждой цифры (с приписанными начальными нулями).
Например, 234 = 10 112, 158 = 001 1012, 1016 = 0001 00002. Эта закономерность позволяет
сформулировать правила перевода чисел в системах, основания которых являются степенями
двойки.
Правило 6. Для перевода числа из системы с основанием 2m в двоичную достаточно
представить в двоичной записи каждую цифру числа (дописывая при необходимости нули
так, чтобы каждая цифра в исходной системе была представлена m двоичными цифрами).
Примеры
Переведём число 424538 из восьмеричной и число 5D16 из шестнадцатеричной системы
в двоичную.
Поскольку 8=23, то каждую цифру первого числа нужно представить трёхзначным
кодом:
424538 = 100 010 100 101 0112.
13.
Поскольку 16=24, то каждую цифру второго числа нужно представить четырёхзначнымкодом:
5D16 = 0101 11012.
Во втором примере начальный ноль записан для наглядности, в ответе его писать не нужно.
Итак, получили 424538 = 1000101001010112 ; 5D16 = 10111012.
Правило 7. Для перевода двоичного числа в систему с основанием 2n достаточно разбить
цифры числа на группы по n цифр (отсчитывая от запятой влево и, если есть дробная часть,
вправо) и осуществить перевод каждой группы отдельно.
Примеры
Переведём
число
10101000101011,11012
в
четверичную,
восьмеричную
и
шестнадцатеричную системы.
Для перевода в четверичную систему (4=22) разобьём цифры числа на группы по
2 цифры (отсчитывая от запятой влево и вправо) и осуществим перевод каждой группы
отдельно:
10 10 10 00 10 10 11,11 012 = 2220223,314
Для перевода в восьмеричную систему (8=23) разобьём цифры числа на группы по
3 цифры (отсчитывая от запятой влево и вправо). При этом требуется дописать начальный
ноль в крайней левой группе и два нуля в конце числа. После этого осуществим перевод
каждой группы отдельно:
010 101 000 101 011,110 1002 = 25053,648
Для перевода в шестнадцатеричную систему (16=24) разобьём цифры числа на группы
по 4 цифры (отсчитывая от запятой влево и вправо), дописав начальные нули в крайней
левой группе. После этого осуществим перевод каждой группы отдельно:
0010 1010 0010 1011,11012 = 2A2B, D 16
Упражнение 12
Переведите:
А) 2131220304 в восьмеричную и шестнадцатеричную системы,
Б) число 2F61B16 в четверичную и восьмеричную системы.
Перевод чисел с периодической дробной частью
Переведем число 0,63(17)8 в 4-ную систему счисления.
14.
Переведем сначала число из восьмеричной системы в двоичную. Представляем каждую3
цифру двоичным кодом (т.к. 8=2 , то группы должны содержать по три цифры):
0,63(17)8 = 0,110 011 (001 111)2
2
Т. к. 4=2 , то отделяем в двоичной записи группы по две цифры (при этом период
повторим несколько раз):
0,63(17)8 = 0, 11 00 11 00 11 11 00 11 11 00 11 11 … 2
Переводим каждую группу из двух двоичных цифр в четверичную систему:
0,63(17)8 = 0, 3 0 3 0 3 3 0 3 3 0 3 3 … 4
Выделяем в полученном числе период. Заметим, что повторяются три цифры – две
тройки и ноль, то есть периодом может быть либо последовательность 330, либо 303, либо
033. Для того, чтобы найти ту цифру, с которой начинается период, будем группировать по
три цифры и сдвигаться на цифру от запятой вправо, если последовательности, стоящие в
соседних скобках, окажутся не одинаковыми:
0,63(17)8 = 0, ( 3 0 3 ) ( 0 3 3 ) 0 3 3 0 3 3 … 4
0,63(17)8 = 0, 3 ( 0 3 0 ) ( 3 3 0 ) 3 3 0 3 3 … 4
0,63(17)8 = 0, 3 0 ( 3 0 3 ) ( 3 0 3 ) ( 3 0 3 ) 3 … 4
Таким образом, 0,63(17)8 = 0,30(303)4 .
Упражнение 13
Перевести число 0,11(12)4 в двоичную, восьмеричную и шестнадцатеричную системы.
15.
Решения и ответы к упражнениямУпражнение 1
А) 91, 23, 472, 1919
Б) XVII, XLVIII, CCXCIII, CMLXV, MMX
Упражнение 2
Цифры в 13-ричной системе
0 1 2 3 4 5 6 7 8 9 A
B
C
Значения в десятичной системе 0 1 2 3 4 5 6 7 8 9 10 11 12
Упражнение 3
а) 101001110,01012 = 1·2-4 + 0·2-3 + 1·2-2 + 0·2-1 + 0·20 + 1·2 + 1·22 + 1·23 + 0·24 + 0·25 +
+ 1·26 + 0·27 + 1·28;
б) 2548 = 4·80 + 5·81 + 2·82;
в) 2D716 = 7⋅160 + D·161 + 2·162
Упражнение 4
101001110,01012 = 1·2-4 + 0·2-3 + 1·2-2 + 0·2-1 + 0·20 + 1·2 + 1·22 + 1·23 + 0·24 + 0·25 +
+ 1·26 + 0·27 + 1·28 = 0,0625 + 0,25 + 2 + 4 + 8 + 64 + 512 = 588,3125
2548 = 4·80 + 5·81 + 2·82 = 4 + 40 + 128 = 172
2D716 = 716⋅160 + D16·161 + 216·162 = 7 + 13·16 + 2·256 = 727
Упражнение 5
973
2
972 486
2
1 486 243
2
0 242 121 2
1 120 60
1 60
0
973 = 11110011012
2
30
30
0
2
15
14
1
2
7
6
1
2
3
2
1
2
1
0
1
2
0
16.
973 = 330314973 = 17158
Упражнение 6
0,8125 = 0,11012 = 0,314 = 0,648 = 0,D16
Упражнение 7
0,92 ≈ 0,111012, 0,92 ≈ 0,322324, 0,92 ≈ 0,727028, 0,92 = 0,(EB851)16
Упражнение 8
813,6875 = 1100101101,10112 = 30231,234 = 1455,548 = 32D,B16.
973 = 3CD16
17.
Упражнение 90
0
1
2
3
4
5
6
+
0
1
2
3
4
5
6
1
1
2
3
4
5
6
10
2
2
3
4
5
6
10
11
3
3
4
5
6
10
11
12
4
4
5
6
10
11
12
13
5
5
6
10
11
12
13
14
×
0
1
2
3
4
5
6
6
6
10
11
12
13
14
15
0
0
0
0
0
0
0
0
1
0
1
2
3
4
5
6
Упражнение 10
A) 10000000112; 2273,58; 61C,516
перенос
1
0
1
1
1
1
1
1 0 0 0 1 1
+ 1 0 1 1 0 0
1
1 1 1 0
0 1 0 1
1 0 1 0 0 0 0 0 0 1 1
перенос
2
2
2
1
1
1 4 5 3 , 3
+
6 2 0 , 2
2 2 7 3 , 5
3 4
+ 2 D
8
8
8
4
, 1
, 4
6 1 C , 5
8
Б) 10011111011002; 4666,28; 2B7,F16
×
перенос
0
0 0
1 1 0
1 1 0 0
1
0
0
0
1
1
1
1
1 1
1
0 0
1 0
0 0
0 0
1 1
1 0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
1 0
1 0
0 0
0
1 0 0 1 1 1 1 1 0 1 1 0 0
2
2
2
2
16
16
16
2
0
2
4
6
11
13
15
3
0
3
6
12
15
21
24
4
0
4
11
15
22
26
33
5
0
5
13
21
26
34
42
6
0
6
15
24
33
42
51
18.
17 7,
2 3,
×
34
+3
4
+3
3
+2
2
+1
34
+2
20
0
7
7
6
25
+2
25
+1
14
4
5
7
6
16
+1
16
+1
10
3
7
7
0
3
+1
14
+2
25
+1
15
+1
4
4
12
8
×
8
0
4 6 6 6, 2 0
1 0,
2 A,
6
8
8
0
+3
30
0
8
3
A
0
+3
3C
C
A
3
2
0
C
2
0
C
2
A
+1
17
2 B 7, F 0
8
16
16
16
В*) 10100001112 ; 1356,18 ; 12E,D16
1 1
перенос
0 0 0 0 1
-1
+10
–
1 0
1 5 2
0
1
0
2
-1
+10-1
+10-1
+10
1 0 0 0 0
0
1
1
2
1 0 0 0 0
1
1
1
2
, 5
8
3 6
3
, 2
8
– 2 3
9
,
D
16
1 1 1 5
, 3
8
1 2
E
, D
16
перенос
-1
–
4 0
0
+10
-1
8
,
+10-1
A
16
+10
Г*) 110002 ; 1338; 6116 .
1 0 0 1 1 1 0 0 02 1 1
1 1 0 1
1 1
0 12
4 3 4 38 3 18
0 0 02
3 1
1 1 0 1
1 2 4
1 1 0 1
1 1 3
0
1 3
1 1 3
1 1 3
A
3 B16
1 B16
A
2
6 116
1 B
1 B
0
0
38
19.
Упражнение 11А) 1010103 = 273 = 20435 = 5407,
Б) 40225 = 254 = 2002223 = 5127,
В) 5467 = 279 = 1011003 = 21045.
Упражнение 12
А) 2131220304 = 1001110110100011002
100 111 011 010 001 1002 = 4732148 ; 0010 0111 0110 1000 11002 = 2768C16
Б) 2F61B16 = 001011110110000110112
10 11 11 01 10 00 01 10 112 = 2331201234 ; 101 111 011 000 011 0112 = 5730338.
Упражнение 13
0,11(12)4 = 0, 01 01 01 10 01 10 01 10 01 10 … 2
0, 01010110011001100110 … 2 = 0,010(0110)2
0, 010 101 100 110 011 001 100 110 … 2 = 0,25(4631)8
0, 0101 0110 0110 0110 0110 … 2 = 0,5(6)16


















 informatics
informatics








