Similar presentations:
Арифметика в позиционных системах счисления
1.
«Арифметическиеоперации в
позиционных
системах счисления»
1
2.
Все позиционные системы счисления «одинаковы», а именно,во всех них выполняются арифметические операции по одним
и тем же правилам:
справедливы
одни и те же законы арифметики:
-коммутативный (переместительный):
m+n=n+m
m·n=n·m
-ассоциативный
(сочетательный): (m + n) + k = m + (n + k) = m + n + k
(m · n) · k = m · (n · k) = m · n · k
-дистрибутивный
(распределительный): (m + n) · k = m · k + n · k
справедливы
правила сложения, вычитания и
умножения столбиком;
правила
выполнения арифметических операций
опираются на таблицы сложения и умножения.
меню
2
3.
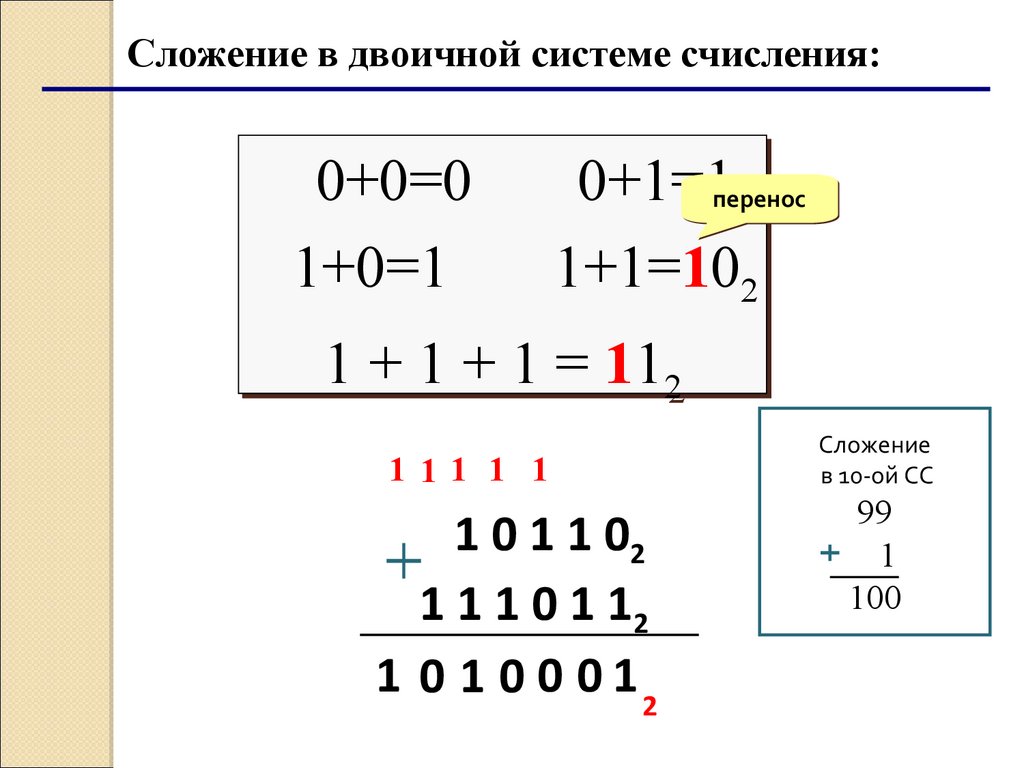
Сложение в двоичной системе счисления:0+0=0
1+0=1
0+1=1перенос
1+1=1022
1 + 1 + 1 = 1122
111 1 1
1 0 1 1 02
1 1 1 0 1 12
1 0 1 0 0 0 12
Сложение
в 10-ой СС
99
1
100
4.
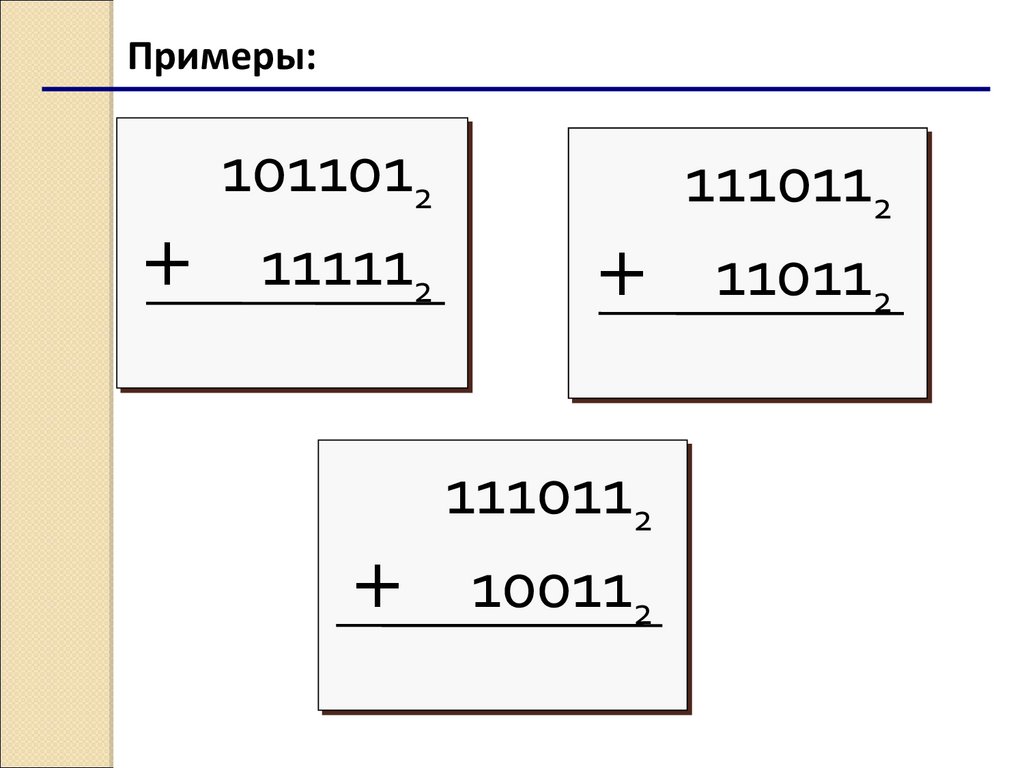
Примеры:10110122
+ 1111122
11101122
+ 1101122
11101122
+ 1001122
5.
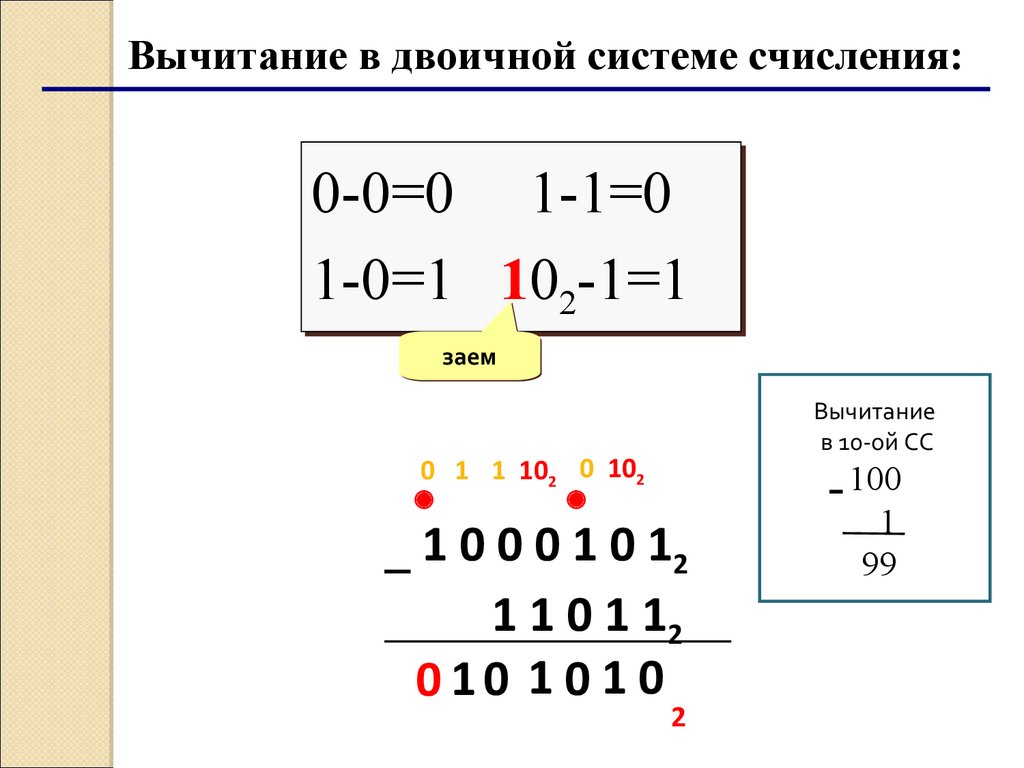
Вычитание в двоичной системе счисления:0-0=0 1-1=0
1-0=1 1022-1=1
заем
Вычитание
в 10-ой СС
0 1 1 102 0 102
1 0 0 0 1 0 12
1 1 0 1 12
0 10 1 0 1 0
2
100
1
99
6.
Примеры:10110122
– 1111122
1101122
– 110122
10101022
– 1001122
меню
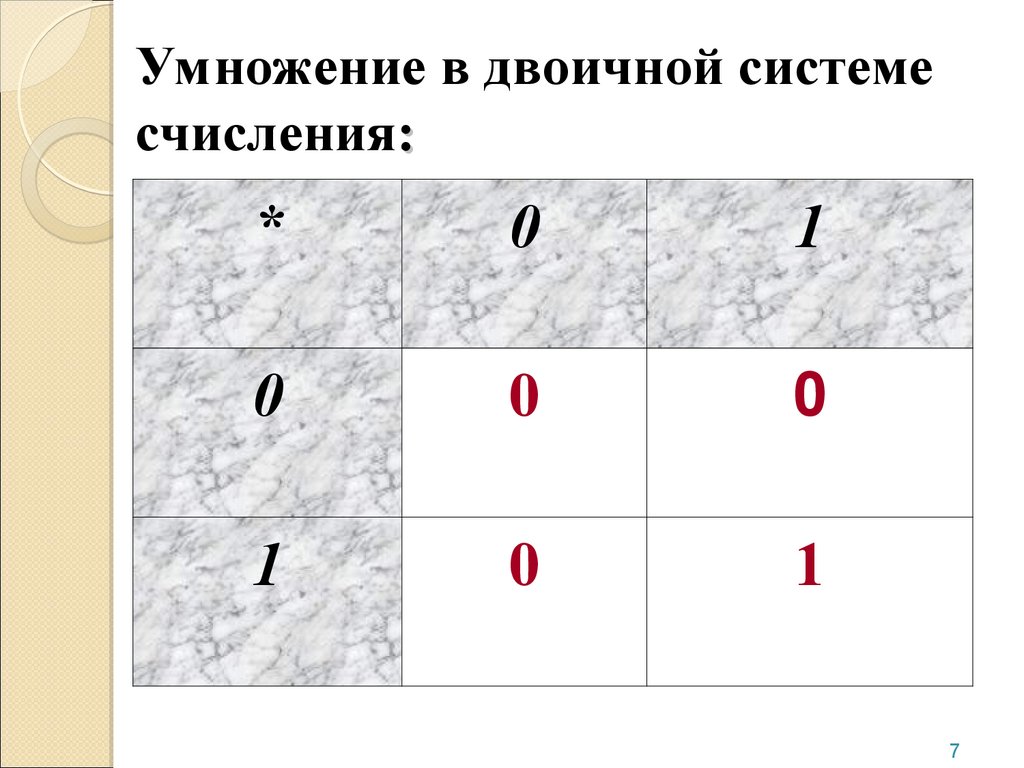
7. Умножение в двоичной системе счисления:
*0
1
0
0
0
1
0
1
7
8.
10110122* 10122
+ 101101
000000
101101
1110000122
1101122
* 110122
101011111
2
меню
8
9.
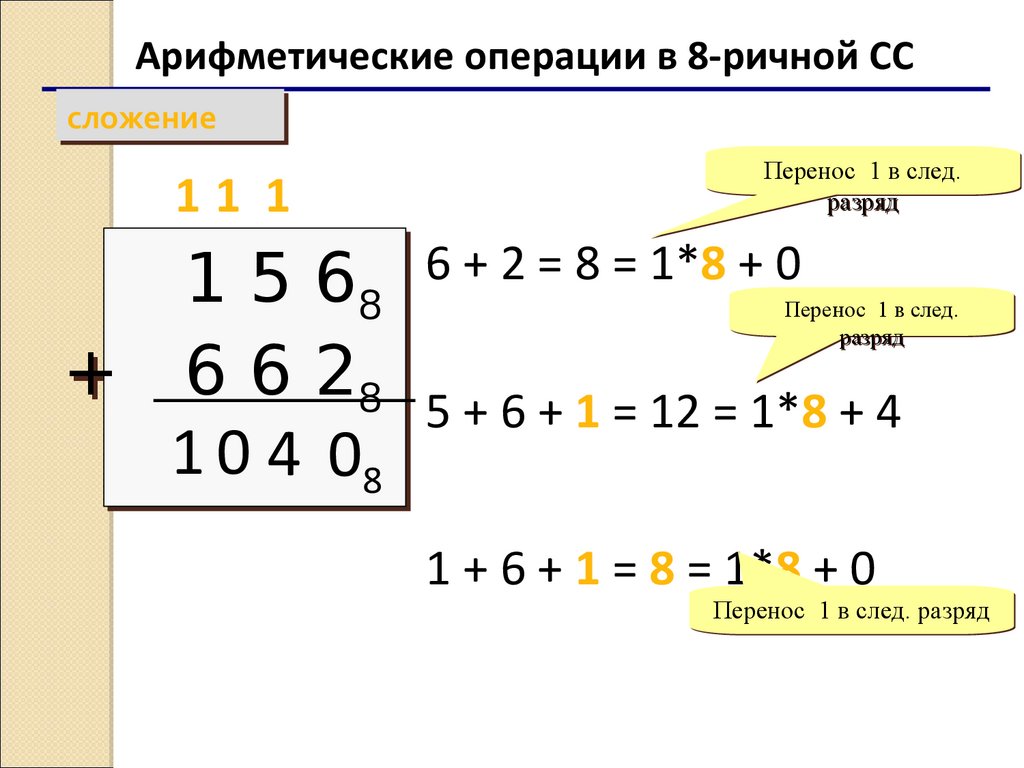
Арифметические операции в 8-ричной ССсложение
сложение
11 1
1 5 688
+ 6 6 288
1 0 4 08
Перенос 1 в след.
разряд
6 + 2 = 8 = 1*8 + 0
Перенос 1 в след.
разряд
5 + 6 + 1 = 12 = 1*8 + 4
1 + 6 + 1 = 8 = 1*8 + 0
Перенос 1 в след. разряд
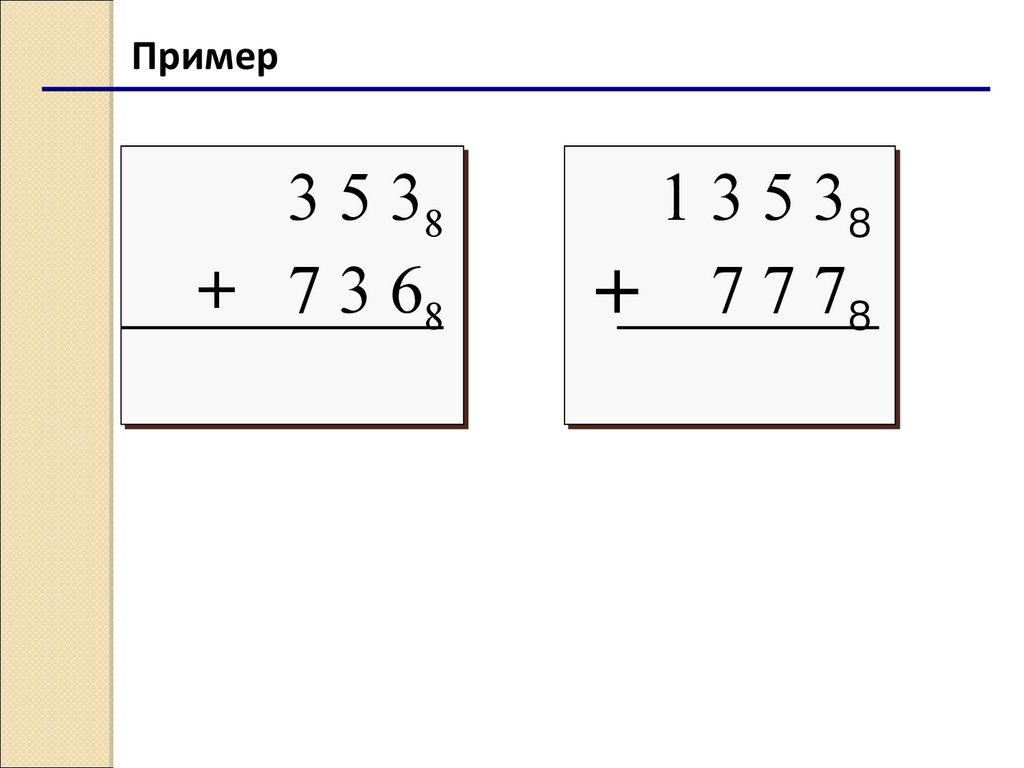
10.
Пример3 5 388
+ 7 3 688
1 3 5 388
+ 7 7 788
11.
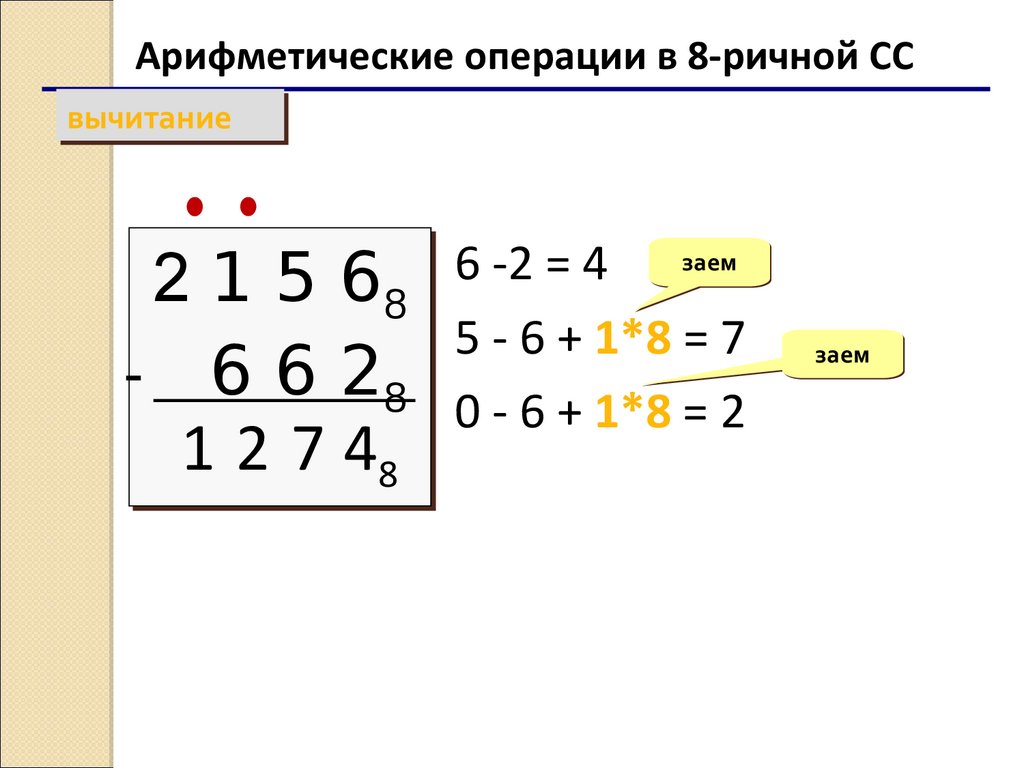
Арифметические операции в 8-ричной ССвычитание
вычитание
2 1 5 688
- 6 6 288
1 2 7 48
6 -2 = 4 заем
5 - 6 + 1*8 = 7
0 - 6 + 1*8 = 2
заем
12.
Примеры4 1 5 388
– 6 6 788
1 1 6 188
– 7 3 288
меню





 informatics
informatics








