Similar presentations:
Приближённые числа и действия над ними
1.
ПРИБЛИЖЁННЫЕЧИСЛА И ДЕЙСТВИЯ
НАД НИМИ
2.
Основные определенияМодель – упрощённое представление о
реальном объекте, процессе или
явлении
Моделирование – построение моделей
для исследования и изучения объектов,
процессов или явлений
3.
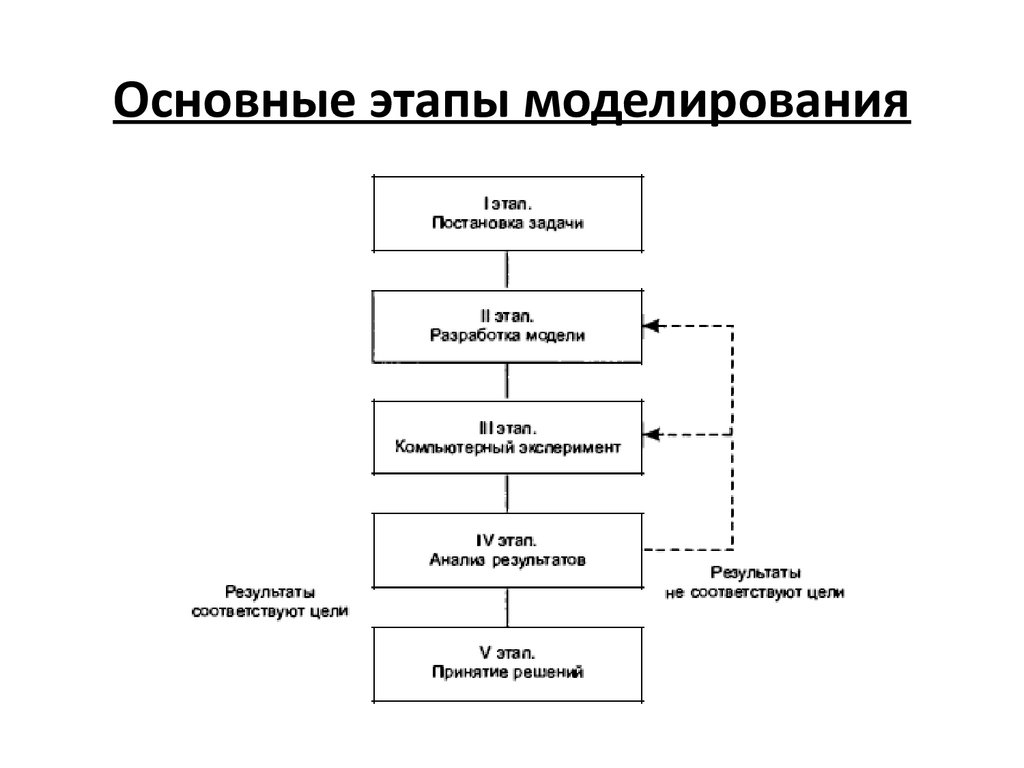
Основные этапы моделирования4.
Основные определенияМатематическая модель – совокупность
математических формул, отражающих связь
различных параметров объекта или процесса
Математическое моделирование – метод
исследования
объектов
и
процессов
реального мира с помощью математических
моделей
5.
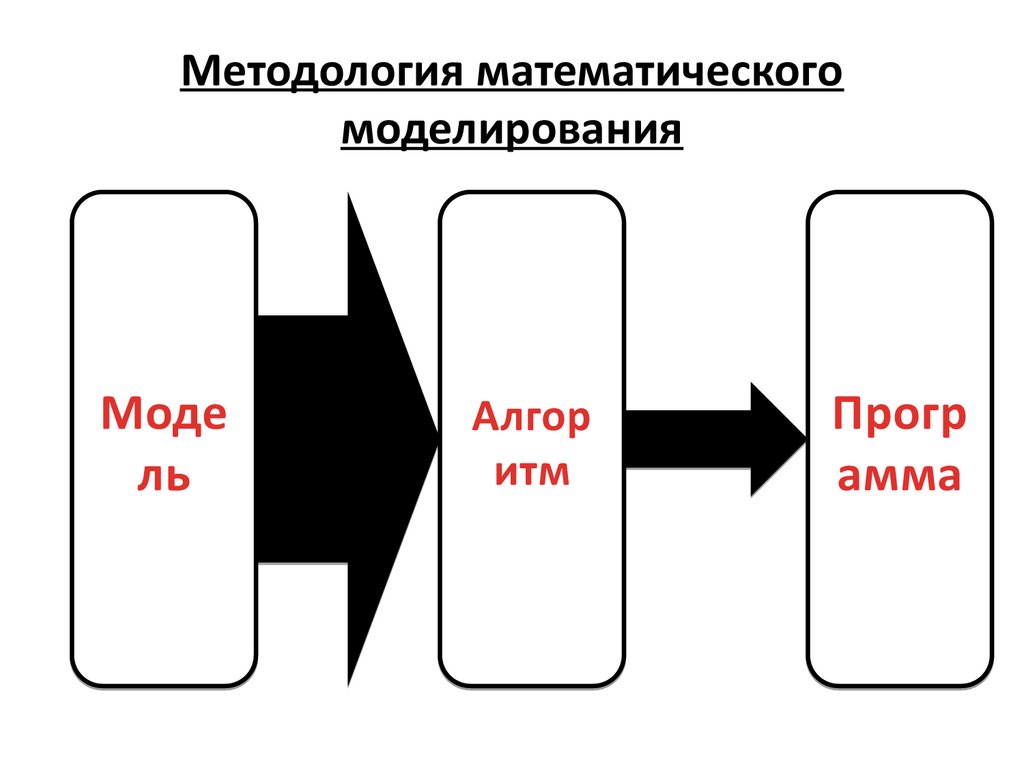
Методология математическогомоделирования
Моде
ль
Алгор
итм
Прогр
амма
6.
Особенности математическогомоделирования
• этап разработки модели:
выбранная или построенная модель должна в математической форме
отражать важнейшие свойства изучаемого процесса;
модели реальных процессов являются достаточно сложными (содержат
системы нелинейных дифференциальных уравнений в частных производных);
исследование
модели аналитическими средствами прикладной математики
позволяет получить предварительные знания об объекте;
7.
Особенности математическогомоделирования
• этап разработки алгоритма:
выбранный или разработанный вычислительный алгоритм не должен
искажать основные свойства модели;
алгоритм должен адаптироваться к особенностям решаемой задачи и
используемым вычислительным средствам;
для
изучения
математической
вычислительной математики;
модели
применяются
методы
8.
Особенности математическогомоделирования
• этап разработки программы:
учёт
специфики
математического
моделирования
(необходимость
использования набора моделей и многовариантность расчётов);
отладка и тестирование программы на решении набора пробных задач;
полное
исследование
математической
модели
для
получения
качественных и количественных характеристик исследуемого объекта;
9.
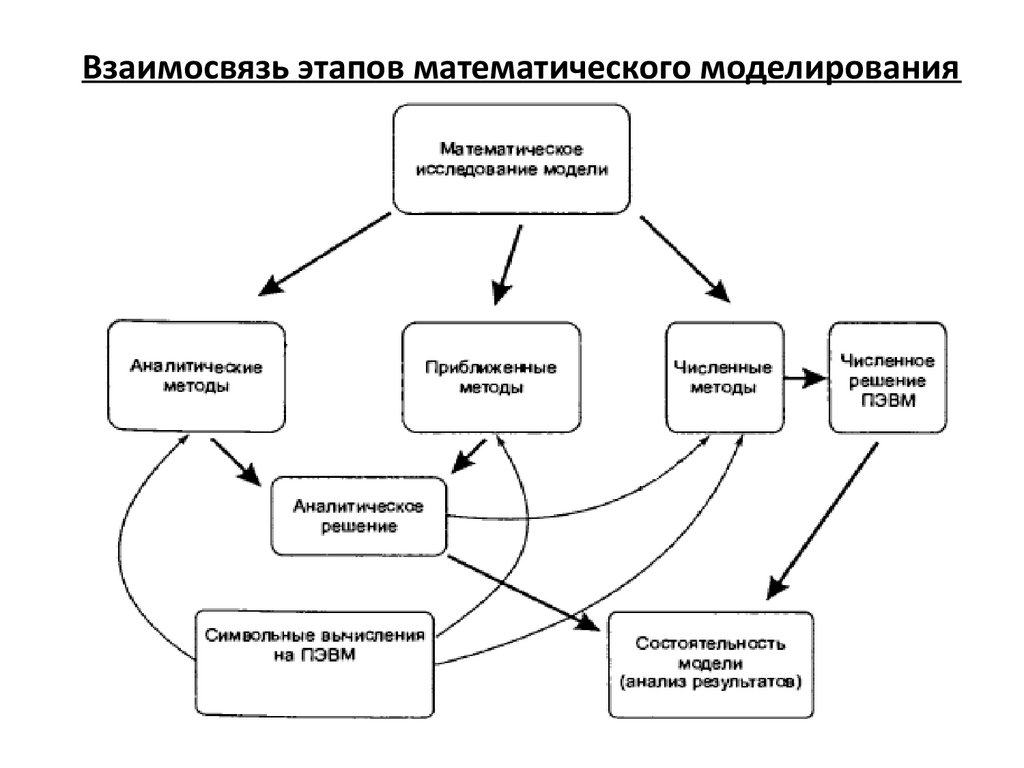
Взаимосвязь этапов математического моделирования10.
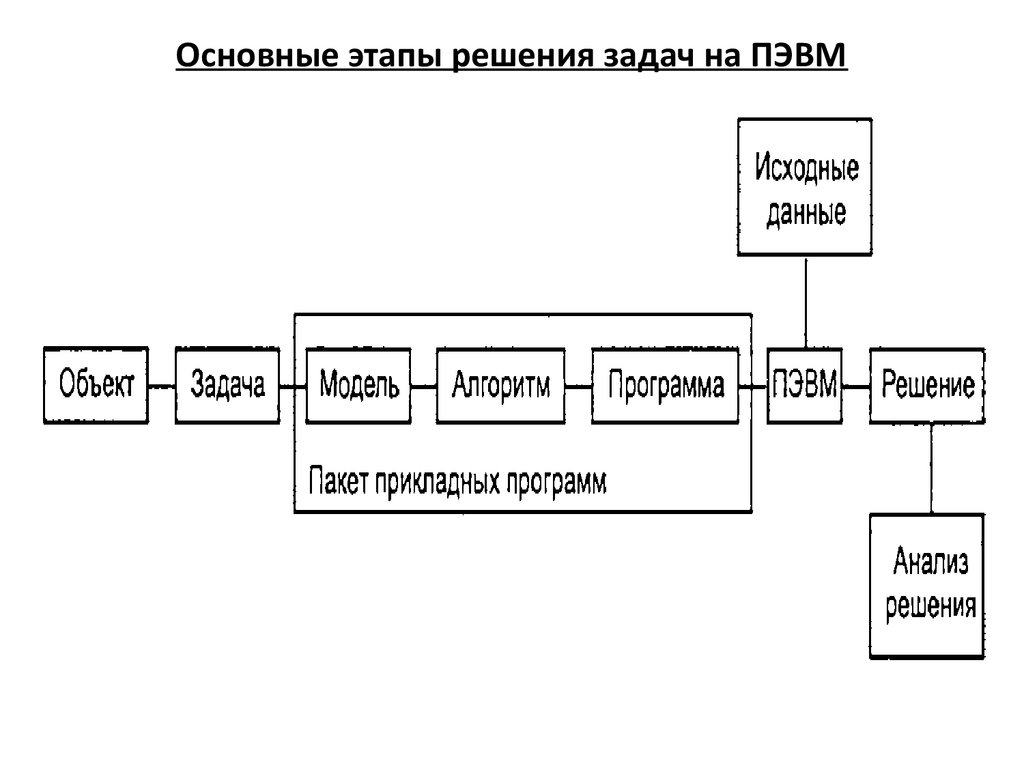
Основные этапы решения задач на ПЭВМ11.
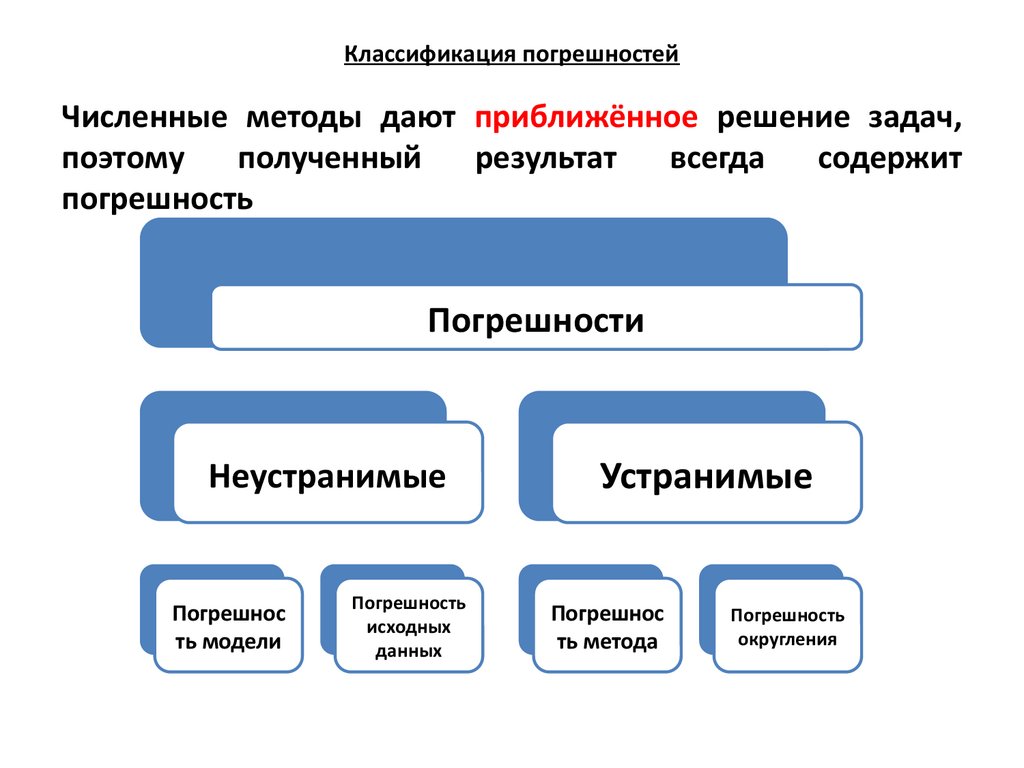
Классификация погрешностейЧисленные методы дают приближённое решение задач,
поэтому
полученный
результат
всегда
содержит
погрешность
Погрешности
Неустранимые
Погрешнос
ть модели
Погрешность
исходных
данных
Устранимые
Погрешнос
ть метода
Погрешность
округления
12.
Классификация погрешностей• погрешность модели:
процесс моделирования связан с упрощением изучаемого
явления;
упрощение явления вносит погрешность в его описание;
• погрешность исходных данных:
математическая модель содержит параметры, зависящие
от исходных данных;
исходные данные определяются в результате измерений,
выполненных с погрешностью;
13.
Классификация погрешностей• погрешность метода:
вычисления в рамках модели можно проводить
различными способами;
сложная математическая задача заменяется более
простой, при этом возникает погрешность метода
вычислений;
• погрешность округлений:
расчеты, выполняемые вручную или с помощью
вычислительной техники, проводятся с конечным числом
цифр;
возникает необходимость округления промежуточных
результатов и окончательного ответа;
погрешность округления может накапливаться в ходе
вычислений;
14.
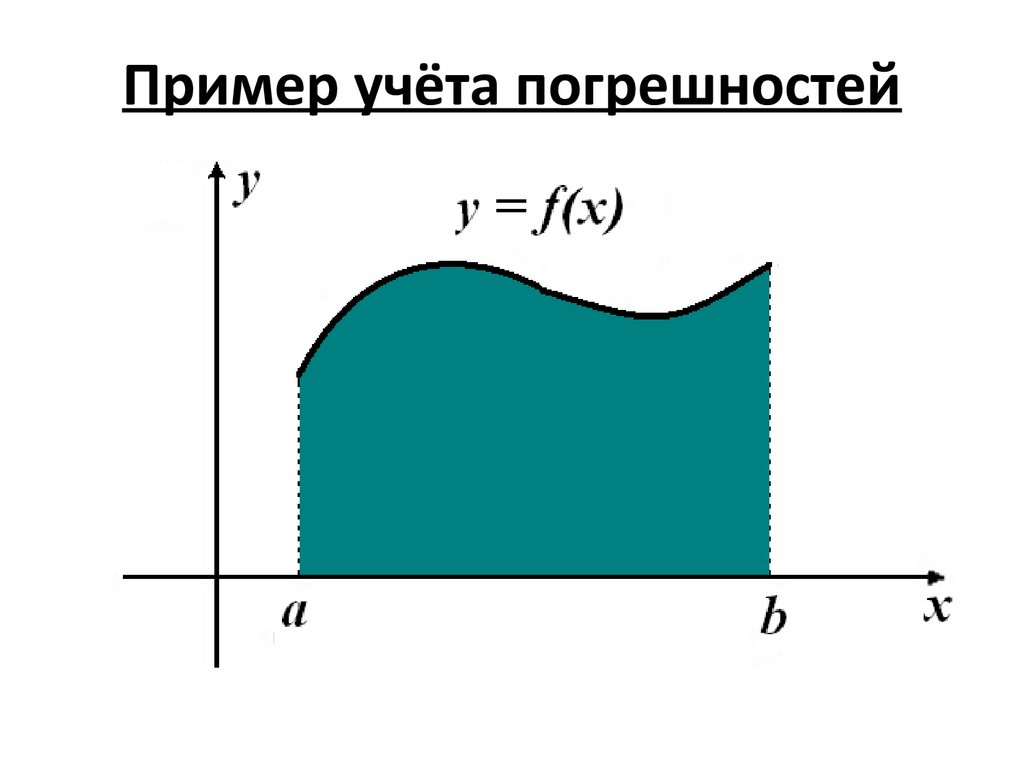
Пример учёта погрешностей15.
Пример учёта погрешностейПостановка задачи:
вычислить площадь фигуры, ограниченной
кривой y = f(x), отрезками прямых x = a
и x = b и осью абсцисс
16.
Пример учёта погрешностейМатематическая модель вычисления площади – определённый интеграл
b
f ( x )dx
Погрешность модели определяется:a
погрешностью чисел a и b;
погрешностью функции y = f(x);
17.
Пример учёта погрешностейМетод вычисления интеграла – расчёт
интегральной суммы
n
f ( x ) x
i
i 1
i
18.
Пример учёта погрешностейS – точное значение площади
S1 – точное значение интеграла
S2 – точное значение интегральной суммы
S3 – результат вычисления интегральной суммы
19.
Пример учёта погрешностейРасчётная формула
Вид погрешности
S – S1
неустранимая погрешность
S 1 – S2
погрешность метода
S 2 – S3
вычислительная погрешность
S – S3
полная погрешность
20.
Абсолютная и относительнаяпогрешности чисел
x – точное значение величины (неизвестно!)
~
Приближённое значение x числа x – число,
мало отличающееся от x и заменяющее его
в вычислениях
Погрешность характеризует точность измерения
приближённого числа
21.
Абсолютная и относительнаяпогрешности чисел
Абсолютная погрешность x~
приближённого числа
~
x~ x x
Предельная абсолютная погрешность *x~
приближённого числа
*
~
x x x~
22.
Абсолютная и относительнаяпогрешности чисел
Относительная погрешность x~
приближённого числа
x~
x~ ~
x
Предельная относительная погрешность x~*
приближённого числа
*
*
x~
x~ ~
x
23.
Абсолютная и относительнаяпогрешности функции
y f ( x1 , x2 ,..., xn ) – непрерывная
дифференцируемая функция;
x~1 x~1 , x~2 x~2 ,..., x~n x~n – приближённые
значения аргументов.
~y f ( x~ , x~ ,..., x~ )
1
2
n
Тогда
– приближённое
значение функции
24.
Абсолютная и относительнаяпогрешности функции
Абсолютная погрешность ~y функции
n
~y
i 1
f ( x~1 , x~2 ,..., x~n ) x~i
x i
Относительная погрешность ~y функции
n
~y
i 1
ln f ( x~1 , x~2 ,..., x~n ) x~i
x i
25.
Абсолютная и относительнаяпогрешности функции
Прямая задача теории погрешностей –
задача вычисления погрешности функции
при заданных погрешностях аргументов
Обратная задача теории погрешностей –
задача
определения
допустимой
погрешности аргументов по заданной
допустимой погрешности функции
26.
Значащие, верные и сомнительныецифры
Значащая цифра приближённого числа – каждая
цифра в его записи, начиная с первой ненулевой
слева.
Значащая цифра – верная (точная),
если
абсолютная погрешность числа не превышает
единицы разряда, соответствующего этой цифре
Значащая цифра – сомнительная, если она не
является верной
27.
Погрешности результатоварифметических операций
• Абсолютные погрешности:
(a b ) a b
(a b ) a b b a ab( a b )
a a b b a a
( a b )
2
b
b
b
(a m ) ma m 1 a , m Q
28.
Погрешности результатоварифметических операций
• Относительные погрешности:
a a b b a b
(a b )
a b
a b
a
(a b ) a b
b
( a m ) m a , m Q
29.
Правила подсчёта верных цифрПри сложении, вычитании, умножении и
делении количество верных цифр в результате
равно наименьшему количеству верных цифр
среди исходных чисел
При возведении приближённого числа в квадрат
или куб, а также при извлечении квадратного и
кубического корня в результате сохраняется
столько же верных цифр, сколько их было в
исходном числе
30.
Правила подсчёта верных цифрПри вычислении промежуточных результатов
сохраняют 1-2 «запасные» цифры, которые в
окончательном результате отбрасываются
Для получения результата с m верными
цифрами исходные числа берутся с таким
числом цифр, которое обеспечивает m+1
верную цифру в результате
31.
Примеры114,568 + 12,5*0,82 = 125
1) 12,5 * 0,82 = 10,25 10,3
2) 114,568 + 10,3 = 114,6 + 10,3 = 124,9 125
32.
Примерыx
(a b )c
, a 28,35; b 16,23; c 1,7
ab c
a b 44,58
(a b )c 44,58 1,7 75,786 75,8
ab 28,35 16,23 460,1205 460,12
ab c 460,12 1,7 458,42
75,8
x
0,16535 0,17
458,42


























 mathematics
mathematics








