Симметрия физических свойств кристаллов

1.

Физические свойства и их связь с составом и структурой
Симметрия физических свойств кристаллов не может быть ниже
его собственной симметрии (принцип Неймана).
А выше?
Пьер Кюри (1859 – 1906)
Может.
Пьер Кюри сформулировал
универсальный закон
симметрии (диссимметрии)принцип суперпозиции:
В результате наложения нескольких
явлений различной природы, каждое из
которых обладает своей собственной
симметрией, в системе сохраняются
лишь совпадающие элементы
симметрии этих явлений.
1

2.

Все, что растет (и/или движется) по вертикали - LnnP (симметрия
цветка);
Все, что растет (и/или движется) по горизонтали или косо к
поверхности – Р (симметрия листа).
2

3.

3

4.

4

5.

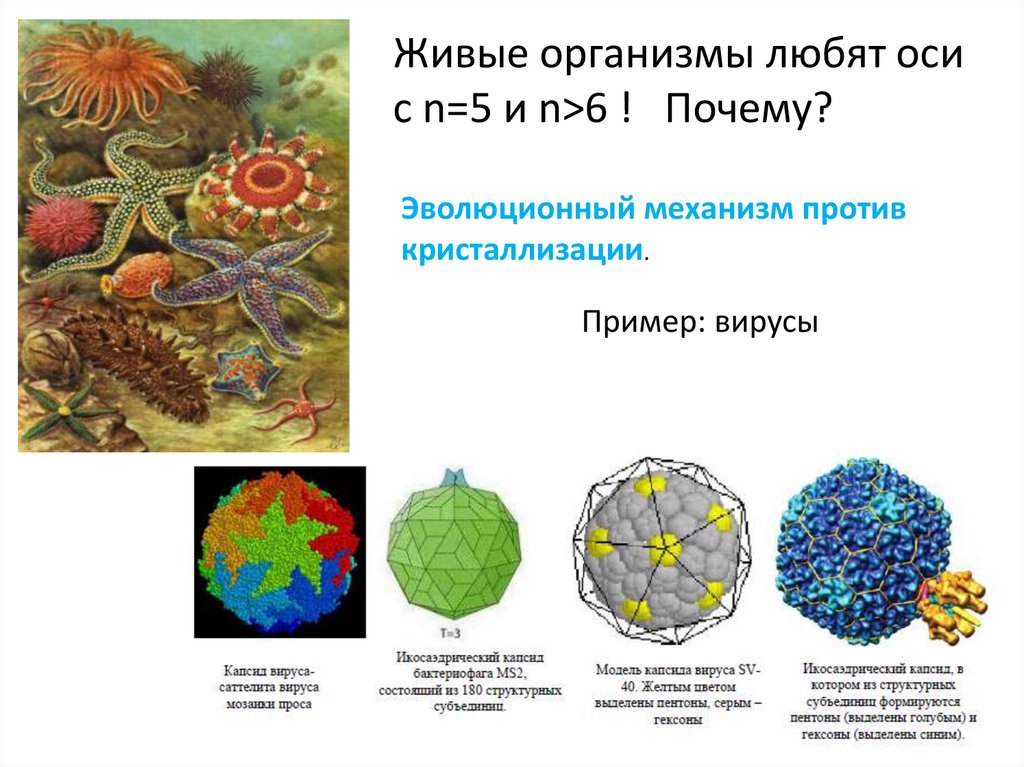
Живые организмы любят оси
с n=5 и n>6 ! Почему?
Эволюционный механизм против
кристаллизации.
Пример: вирусы
5

6.

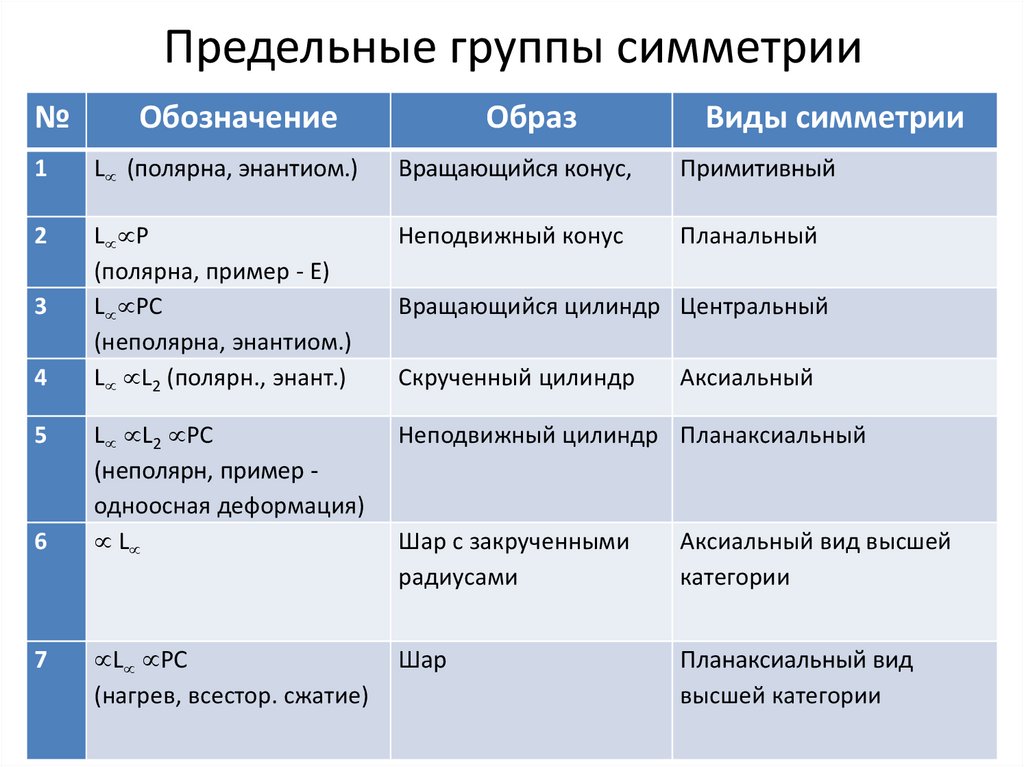
Предельные группы симметрии
№
Обозначение
Образ
Виды симметрии
1
L (полярна, энантиом.)
Вращающийся конус,
Примитивный
2
L P
(полярна, пример - E)
L PC
(неполярна, энантиом.)
L L2 (полярн., энант.)
Неподвижный конус
Планальный
L L2 PС
(неполярн, пример одноосная деформация)
L
Неподвижный цилиндр Планаксиальный
Шар с закрученными
радиусами
Аксиальный вид высшей
категории
L PC
(нагрев, всестор. сжатие)
Шар
Планаксиальный вид
высшей категории
3
4
5
6
7
Вращающийся цилиндр Центральный
Скрученный цилиндр
Аксиальный
6

7.

У реальных кристаллов морфологическая симметрия может быть
как выше, так и ниже истинной (структурной) симметрии. Первый
случай именуется гиперморфией, второй - гипоморфией.
Пример: кристаллы хлората NаСlO3, вид симметрии 3L24L3.
Кристаллы ограняются гранями куба, т.е. морфологическая
симметрия 3L44L36L29РC – гиперморфия (из-за правила Бравэ).
Пример: кристалл кубической сингонии аксиально-центрального
вида симметрии 3L44L36L29РC, растущий в среде с симметрией
конуса , в разных вариантах ориентировки относительно конуса
(L ): L44Р при L4 L ; L33Р при L3 L ; L22Р при L2 L ; Р при Р L
(если ни одна из осей симметрии не совпадает с L ) ; L1, если ни
один элемент симметрии кристалла не параллелен оси L гипоморфия.
В последнем случае сингония внешней формы кристалла
понижается до триклинной.
7

8.

Факторы, определяющие форму кристаллов
1. Принцип Неймана (симметрия, накладываемая внешней средой)
2. Направленность химических связей (внутренняя симметрия(
3. Принцип Ле Шателье – Брауна, принцип Вант-Гоффа Внешние параметры (T, P а
также м.б. H, E)
Принцип Ле Шателье – Брауна : Внешнее воздействие, выводящее систему из
термодинамического равновесия, вызывает в ней процессы, стремящиеся
ослабить эффект этого воздействия.
Т V длины связей до некоторого предела, после чего происходит
перестройка структуры в новую модификацию (КЧ ), размерность сопряжения полиэдров
(вместо общей грани – общее ребро или вершина).
Как правило, симметрия повышается (вплоть до предельной группы в плазме)
P V длины связей до некоторого предела (КЧ = const), после чего
происходит перестройка структуры в новую модификацию (КЧ ), размерность
сопряжения полиэдров (вместо общей вершины – общая грань и т.д.; длины связей при
этом могут даже расти!)
Симметрия повышается (как правило), если сохраняющиеся фрагменты меняют
сопряжение.
Симметрия понижается, если происходит полная перестройка (фрагменты разрушаются).
8

9.

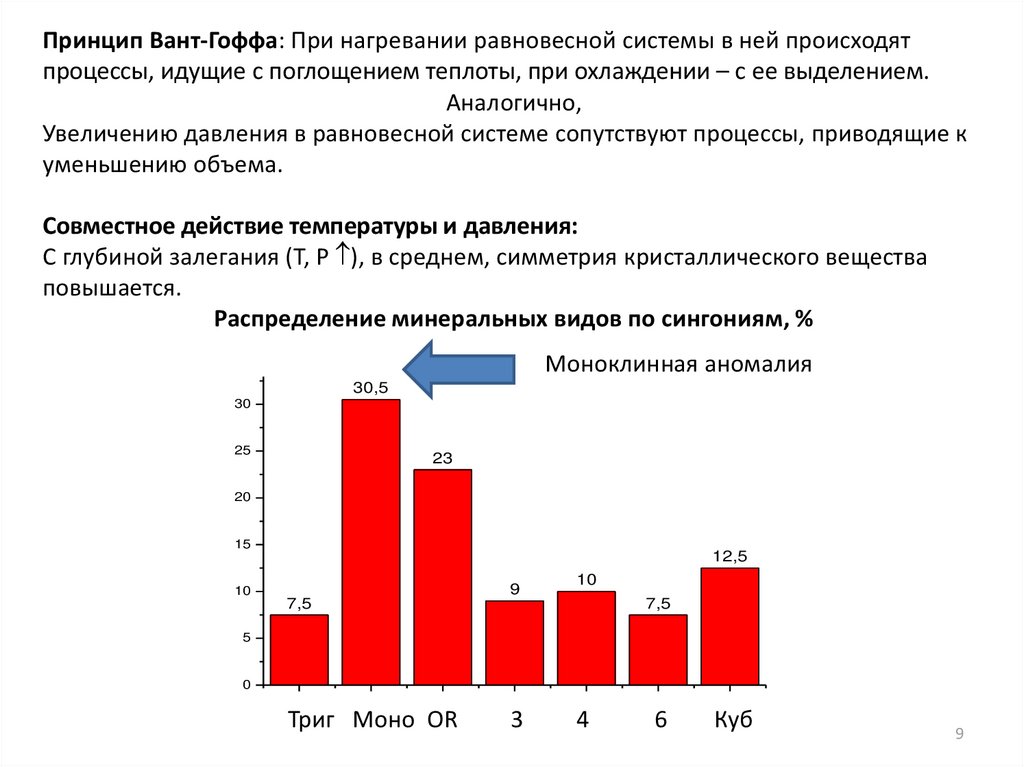
Принцип Вант-Гоффа: При нагревании равновесной системы в ней происходят
процессы, идущие с поглощением теплоты, при охлаждении – с ее выделением.
Аналогично,
Увеличению давления в равновесной системе сопутствуют процессы, приводящие к
уменьшению объема.
Совместное действие температуры и давления:
С глубиной залегания (Т, Р ), в среднем, симметрия кристаллического вещества
повышается.
Распределение минеральных видов по сингониям, %
Моноклинная аномалия
30,5
30
25
23
20
15
10
12,5
9
10
7,5
7,5
5
0
Триг Моно OR
3
4
6
Куб
9

10.

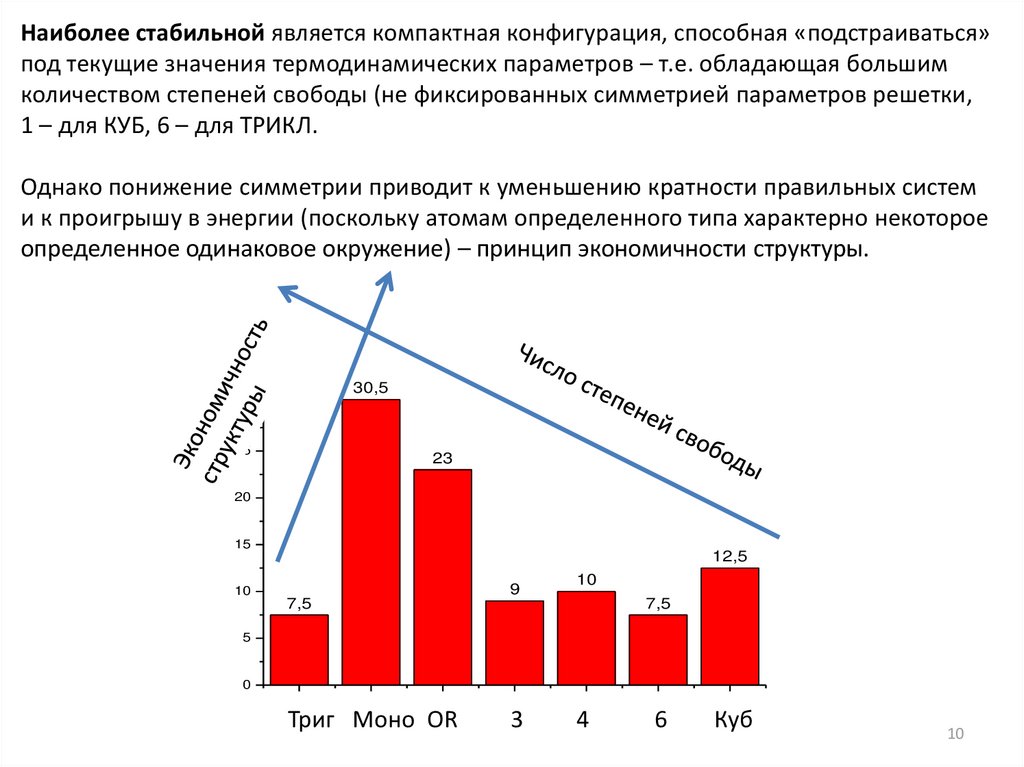
Наиболее стабильной является компактная конфигурация, способная «подстраиваться»
под текущие значения термодинамических параметров – т.е. обладающая большим
количеством степеней свободы (не фиксированных симметрией параметров решетки,
1 – для КУБ, 6 – для ТРИКЛ.
Однако понижение симметрии приводит к уменьшению кратности правильных систем
и к проигрышу в энергии (поскольку атомам определенного типа характерно некоторое
определенное одинаковое окружение) – принцип экономичности структуры.
30,5
30
25
23
20
15
10
12,5
9
10
7,5
7,5
5
0
Триг Моно OR
3
4
6
Куб
10

11.

Морфология кристаллов
Зависит от условий роста
Образование скелетных (а) и антискелетных (б,в) форм
Дендриты (быстрая кристаллизация) и сростки
11

12.

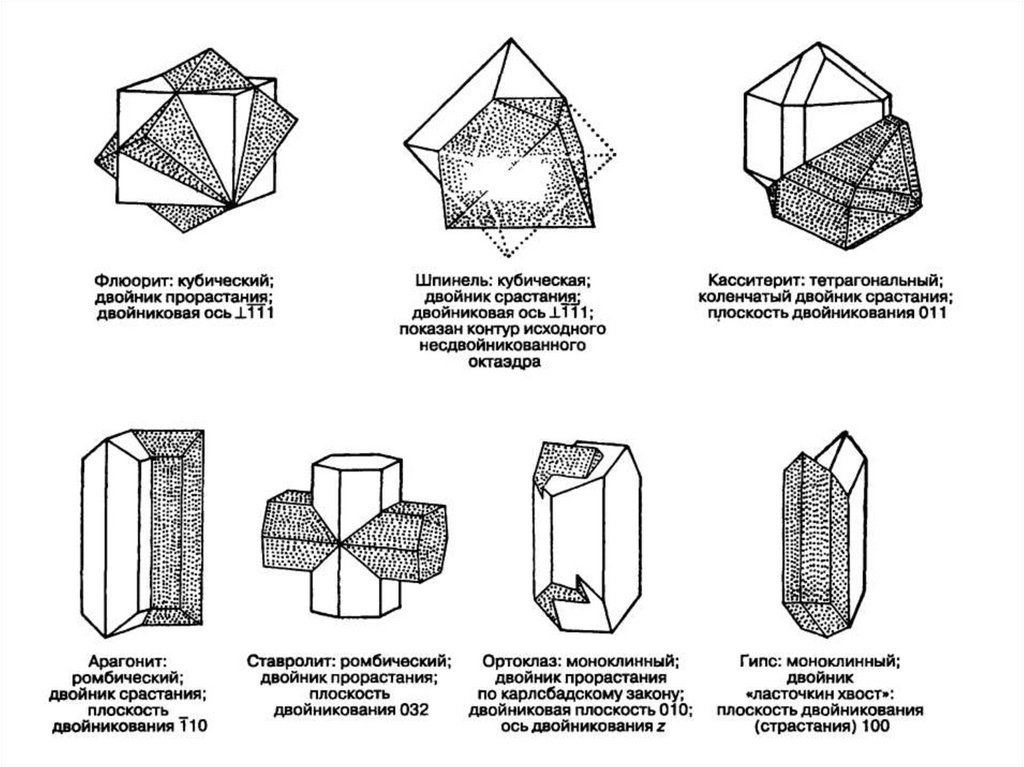
Двойники
Двойники - кристаллические образования, состоящие из двух
или большего числа монокристаллов, разориентированных
друг относительно друга строго закономерно и связанных
симметрическими преобразованиями -
двойниковыми элементами симметрии. Обычно это плоскость
симметрии (двойниковая плоскость), поворотная ось симметрии
2-го порядка (двойниковая ось) и изредка – центр инверсии.
Возможно одновременное присутствие двойниковой плоскости
и двойниковой оси. Для двойниковых элементов симметрии
используют обычные обозначения с индексом tw (англ . twin двойник) - Ltw , mtw , Ctw.
12

13.

13

14.

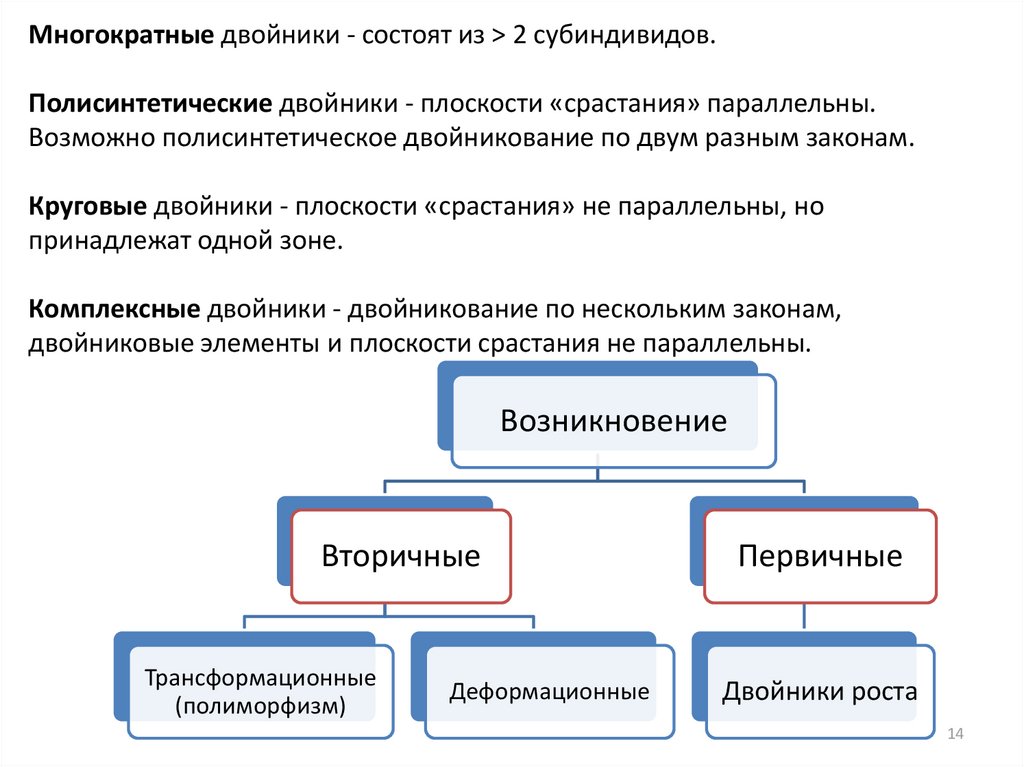
Многократные двойники - состоят из > 2 cубиндивидов.
Полисинтетические двойники - плоскости «срастания» параллельны.
Возможно полисинтетическое двойникование по двум разным законам.
Круговые двойники - плоскости «срастания» не параллельны, но
принадлежат одной зоне.
Комплексные двойники - двойникование по нескольким законам,
двойниковые элементы и плоскости срастания не параллельны.
Возникновение
Вторичные
Трансформационные
(полиморфизм)
Деформационные
Первичные
Двойники роста
14

15.

Эпитаксия
Эпитаксия - структурно закономерное срастание кристаллов
различных веществ.
Условие: близость соответственных периодов решетки.
Пример: рутил (TiO2) на гематите (Fe2O3)
15

16.

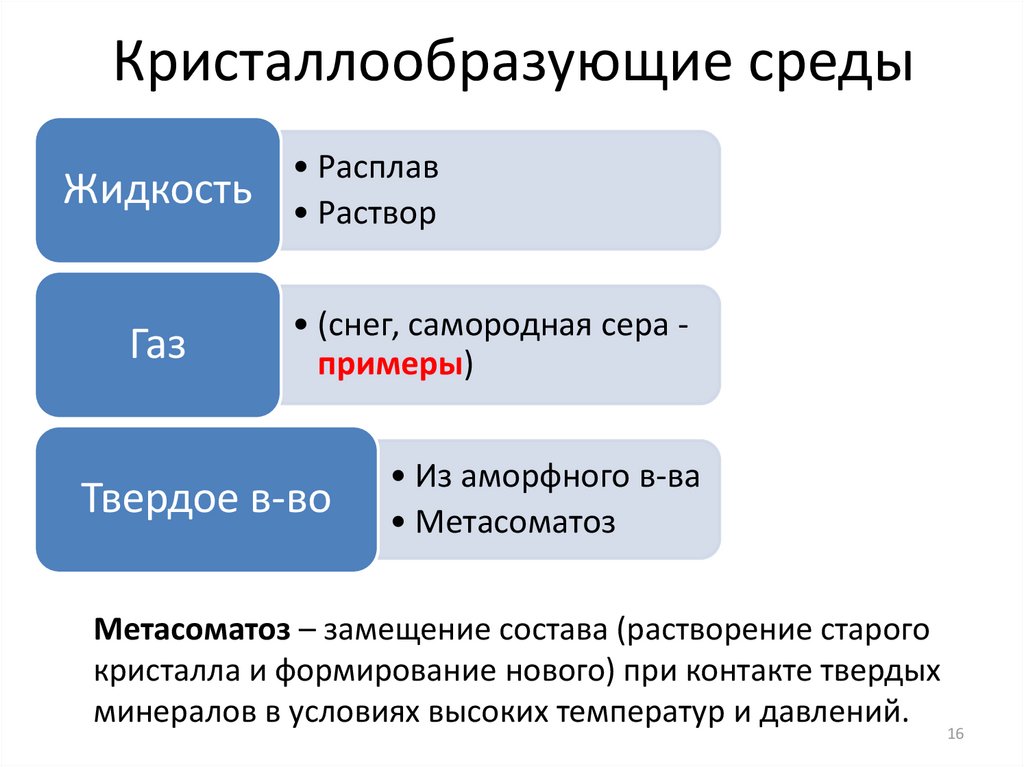
Кристаллообразующие среды
Жидкость
Газ
• Расплав
• Раствор
• (снег, самородная сера примеры)
Твердое в-во
• Из аморфного в-ва
• Метасоматоз
Метасоматоз – замещение состава (растворение старого
кристалла и формирование нового) при контакте твердых
минералов в условиях высоких температур и давлений.
16

17.

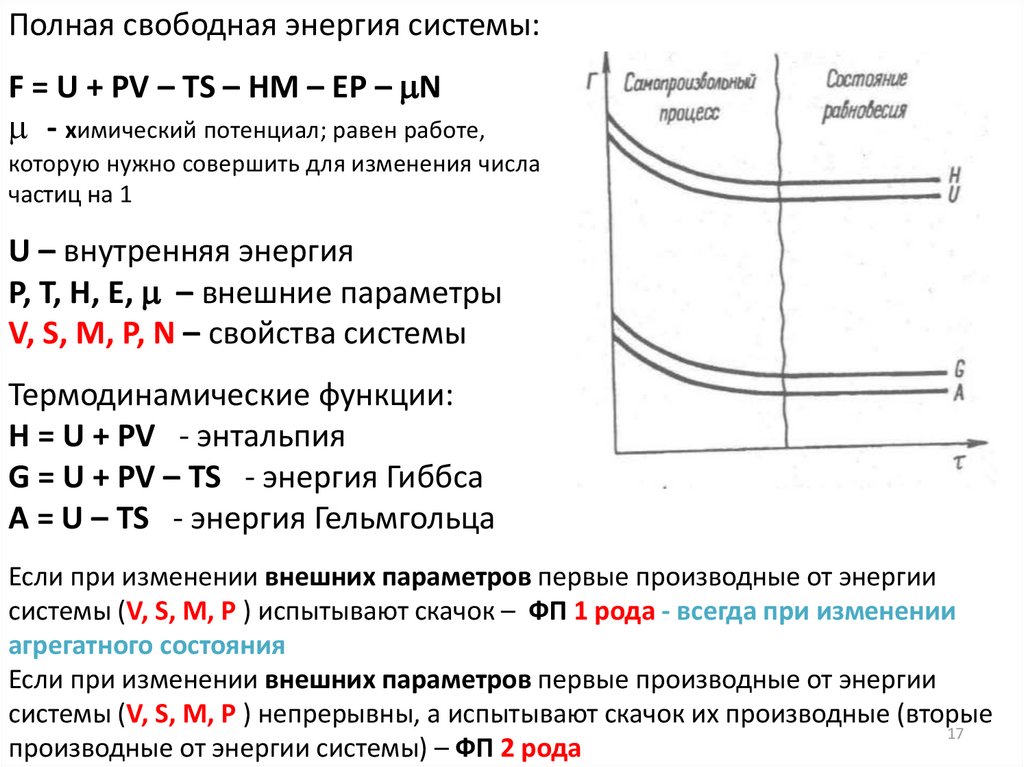
Полная свободная энергия системы:
F = U + PV – ТS – HM – EР – N
- химический потенциал; равен работе,
которую нужно совершить для изменения числа
частиц на 1
U – внутренняя энергия
P, T, H, E, – внешние параметры
V, S, M, P, N – свойства системы
Термодинамические функции:
H = U + PV - энтальпия
G = U + PV – ТS - энергия Гиббса
А = U – ТS - энергия Гельмгольца
Если при изменении внешних параметров первые производные от энергии
системы (V, S, M, P ) испытывают скачок – ФП 1 рода - всегда при изменении
агрегатного состояния
Если при изменении внешних параметров первые производные от энергии
системы (V, S, M, P ) непрерывны, а испытывают скачок их производные (вторые
17
производные от энергии системы) – ФП 2 рода

18.

Кристаллизация в двухфазной
системе (k – кристалл, с – среда)
- условие кристаллизации
Pk = Pc = P – условие отсутствия поверхностного натяжения
(Это очень грубое приближение)
i i Tsi P i – для фазы i, - потенциальная энергия,
s – энтропия, - объем частицы
i ~ Qисп = ~ (10 100 ккал/моль )/ Na ~ (7 - 70) 10-20 Дж.
P i = kT ~ 1,4 10-20 Дж
si = sконфиг + sколеб + sвращ
sколеб
kT
3k ln _
h
- «Простой»
кристалл
_
= 3*1013 сек-1 , Т = 1000 К Tsколеб ~ 3kT ~ 4*10-20 Дж.
18

19.

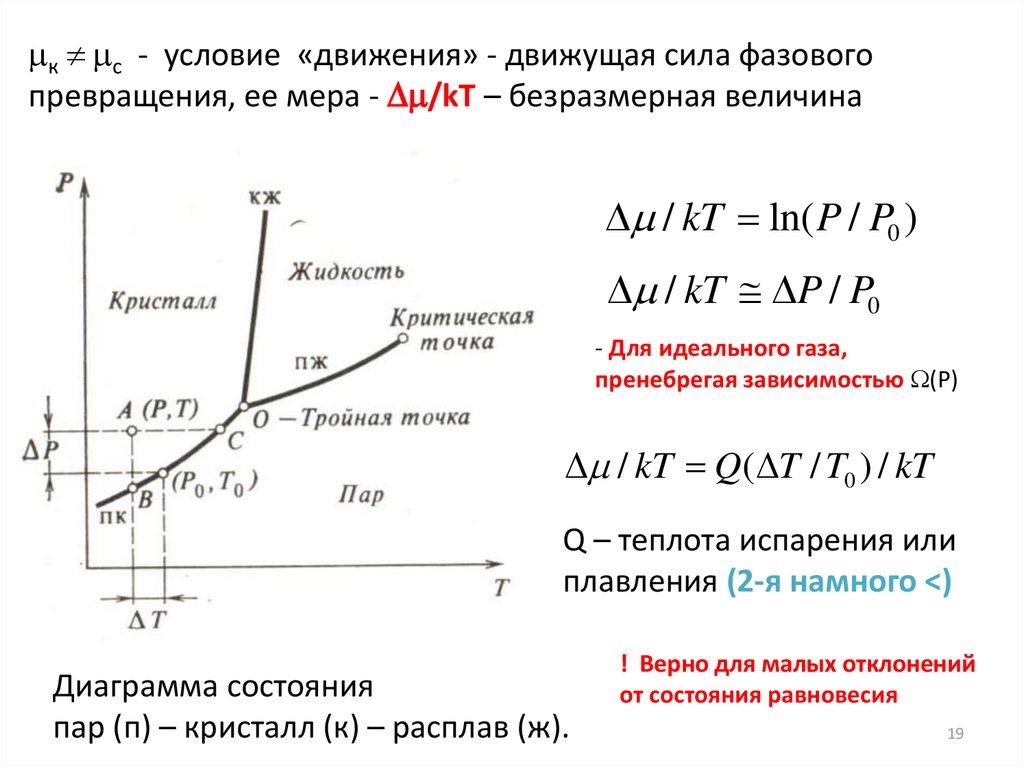
к с - условие «движения» - движущая сила фазового
превращения, ее мера - /kT – безразмерная величина
/ kT ln( P / P0 )
/ kT P / P0
- Для идеального газа,
пренебрегая зависимостью (Р)
/ kT Q( T / T0 ) / kT
Q – теплота испарения или
плавления (2-я намного <)
Диаграмма состояния
пар (п) – кристалл (к) – расплав (ж).
! Верно для малых отклонений
от состояния равновесия
19

20.

Многокомпонентные системы
K 0 X Bкрист / X Bжидк
- Коэффициент захвата
(распределения) компонента
В между кристаллической и
жидкой фазами
/ kT ln C
C0
C / C0
С – концентрация расплава,
С0 – равновесная концентрация
Для неидеальных растворов
вместо концентраций - активности
20

21.

Поверхностная энергия и
периодические цепи связей ПЦС
Поверхностная энергия границы кристалл - вакуум при Т = 0 приближенно
равна полусумме энергий всех связей, которые необходимо разорвать для
формирования поверхности.
Все связи в кристалле можно разбить
на группы отрезков одинаковой
длины вдоль определенных
кристаллографических направлений.
Цепи из отрезков одинаковой длины и
одинаковой ориентации называют
ПЦС.
Для грани (100)
100
100
2a 2
Поверхностная энергия слагается из энергий
тех связей, которые принадлежат к ПЦС,
пересекающих данную поверхность
(есть смысл учитывать только ПЦС с самыми
короткими связями).
21

22.

Закон Браве (из лекции 1)
• Морфологическая значимость грани, то есть ее
относительное развитие на кристалле,
пропорциональна ее ретикулярной плотности.
То есть, кристалл при росте покрывается гранями с
наибольшей ретикулярной плотностью.
• Спайность кристалла (способность скалываться по
определенным плоскостям под действием удара
или давления), как правило, происходит по
плоскостям с наибольшей ретикулярной
плотностью.
22

23.

Поверхностная энергия границы кристалла зависит от ее
кристаллографической ориентации. Главный вклад вносят цепи
наиболее сильных связей.
Для гексаэдра это грани {100} .
Грани ромбоэдра {110} содержат одну систему ПЦС ближайших
соседей и одну вторых.
Грани октаэдра и тетраэдра {111} не содержат ни одной ПЦС
ближайших соседей, но содержат три ПЦС вторых соседей.
Грани, параллельные не менее 2 системам ПЦС ближайших
соседей, называют F-гранями,
параллельные одной системе – S–гранями,
не содержащие ни одной такой ПЦС - K–гранями.
Наибольшая ретикулярная плотность достигается в F-гранях,
поэтому их называют плотноупакованными.
23

24.

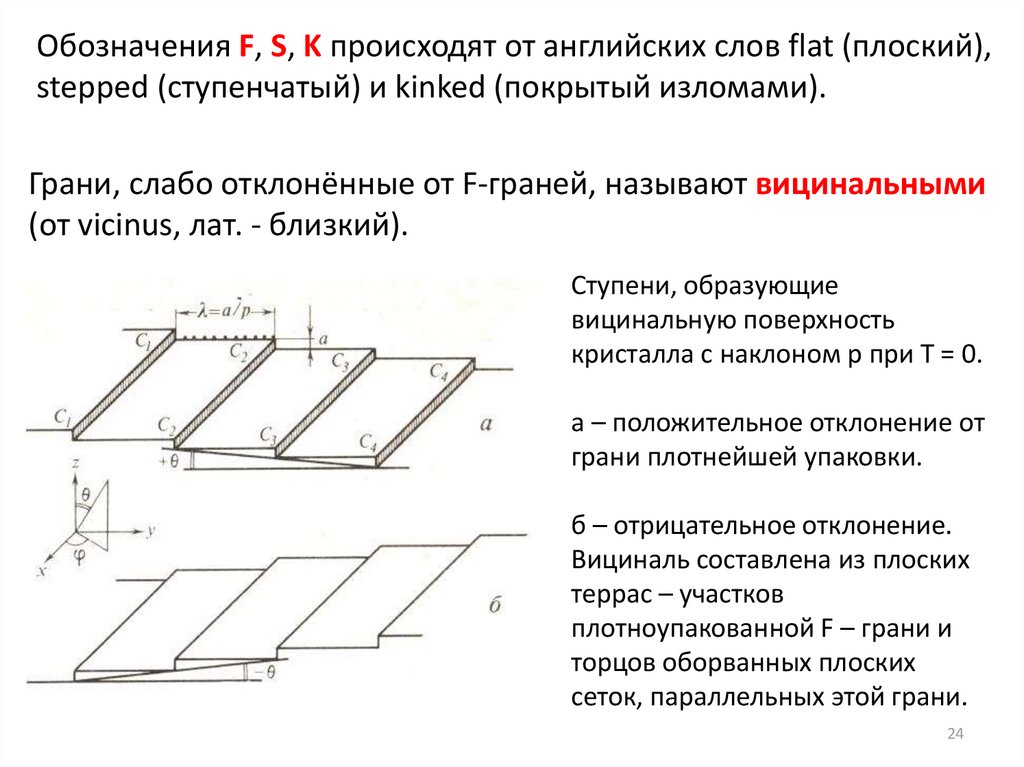
Обозначения F, S, K происходят от английских слов flat (плоский),
stepped (ступенчатый) и kinked (покрытый изломами).
Грани, слабо отклонённые от F-граней, называют вицинальными
(от vicinus, лат. - близкий).
Ступени, образующие
вицинальную поверхность
кристалла с наклоном р при Т = 0.
a – положительное отклонение от
грани плотнейшей упаковки.
б – отрицательное отклонение.
Вициналь составлена из плоских
террас – участков
плотноупакованной F – грани и
торцов оборванных плоских
сеток, параллельных этой грани.
24

25.

Теория роста идеальных кристаллов
Косселя-Странского (1928)
Частицы присоединяются к кристаллу,
максимально понижая энергию системы.
Современная теория роста кристаллов
описывает две стадии:
1) адсорбцию (адатомы) и
2) диффузию.
Если в процессе роста кристалла состав
среды меняется, то в кристалле
формируются зоны или пирамиды роста
(зональный кристалл).
Пример: аметрин (SiO2), состоящий из
аметиста и цитрина.
25

26.

Послойный рост (по Косселю-Странскому)
Рост - встраиванием частиц только в особых местах роста, которыми
служат ступени (минимизация поверхностной энергии).
Ступени на плотноупакованной гладкой (сингулярной) F-грани служат
стоками для адатомов. При росте кристалла ступени на вицинальных
гранях выклиниваются, оставляя сингулярную поверхность,
дальнейший рост которой возможен при появлении новых источников
ступеней.
Источниками ступеней служат двумерные зародыши, дислокации,
места соприкосновения между кристаллом и его контейнером, границы
зёрен между двумя соприкасающимися кристаллами различной
ориентации, инородные макроскопические частицы, двойники и т.д.
Энергии ступеней разного происхождения и частоты присоединения в
них (ступенях) неодинаковы, поэтому выделяют механизм роста
сингулярной грани двумерными зародышами
и дислокационный механизм.
26

27.

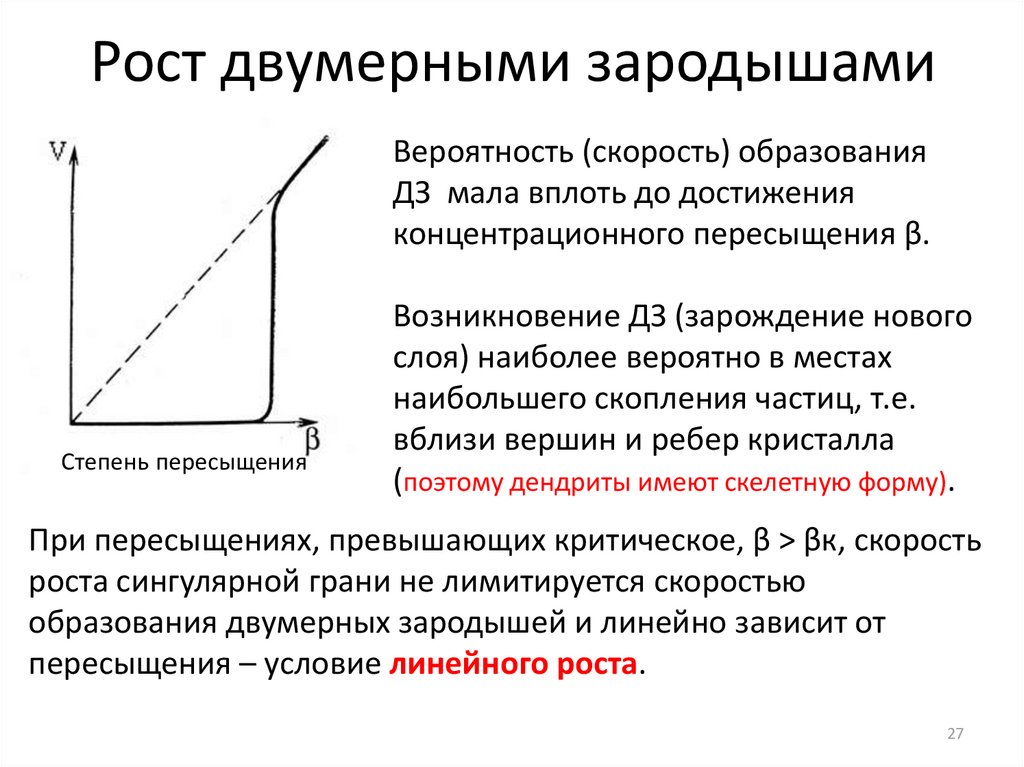
Рост двумерными зародышами
Вероятность (скорость) образования
ДЗ мала вплоть до достижения
концентрационного пересыщения β.
Степень пересыщения
Возникновение ДЗ (зарождение нового
слоя) наиболее вероятно в местах
наибольшего скопления частиц, т.е.
вблизи вершин и ребер кристалла
(поэтому дендриты имеют скелетную форму).
При пересыщениях, превышающих критическое, β > βк, скорость
роста сингулярной грани не лимитируется скоростью
образования двумерных зародышей и линейно зависит от
пересыщения – условие линейного роста.
27

28.

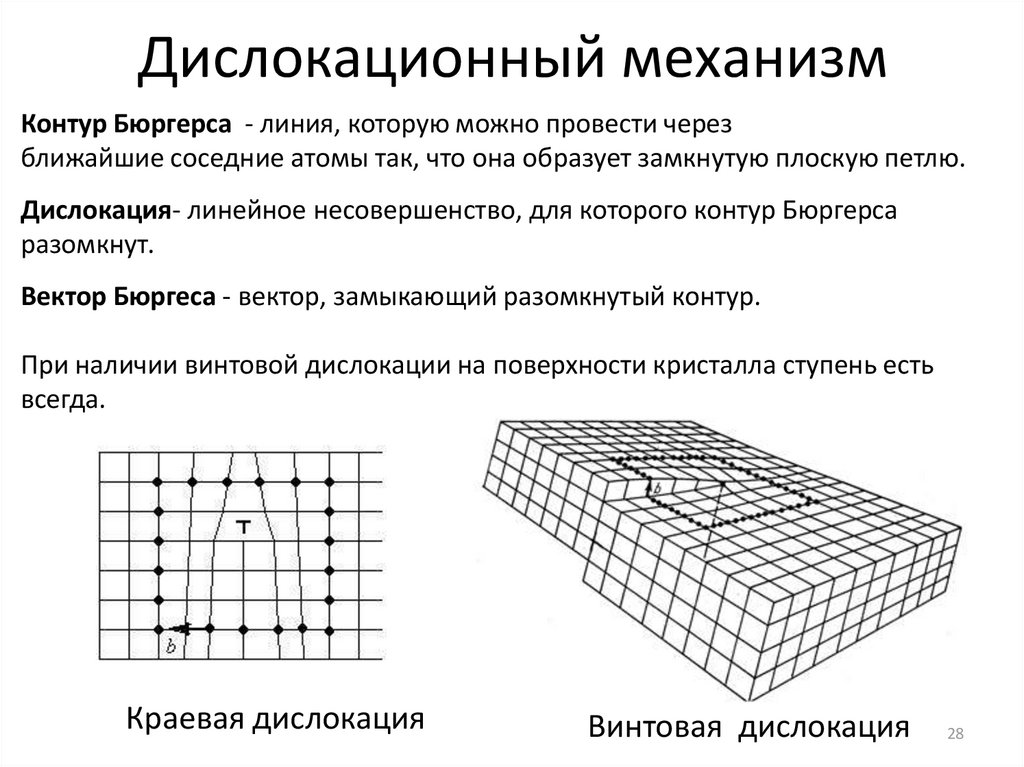
Дислокационный механизм
Контур Бюргерса - линия, которую можно провести через
ближайшие соседние атомы так, что она образует замкнутую плоскую петлю.
Дислокация- линейное несовершенство, для которого контур Бюргерса
разомкнут.
Вектор Бюргеса - вектор, замыкающий разомкнутый контур.
При наличии винтовой дислокации на поверхности кристалла ступень есть
всегда.
Краевая дислокация
Винтовая дислокация
28

29.

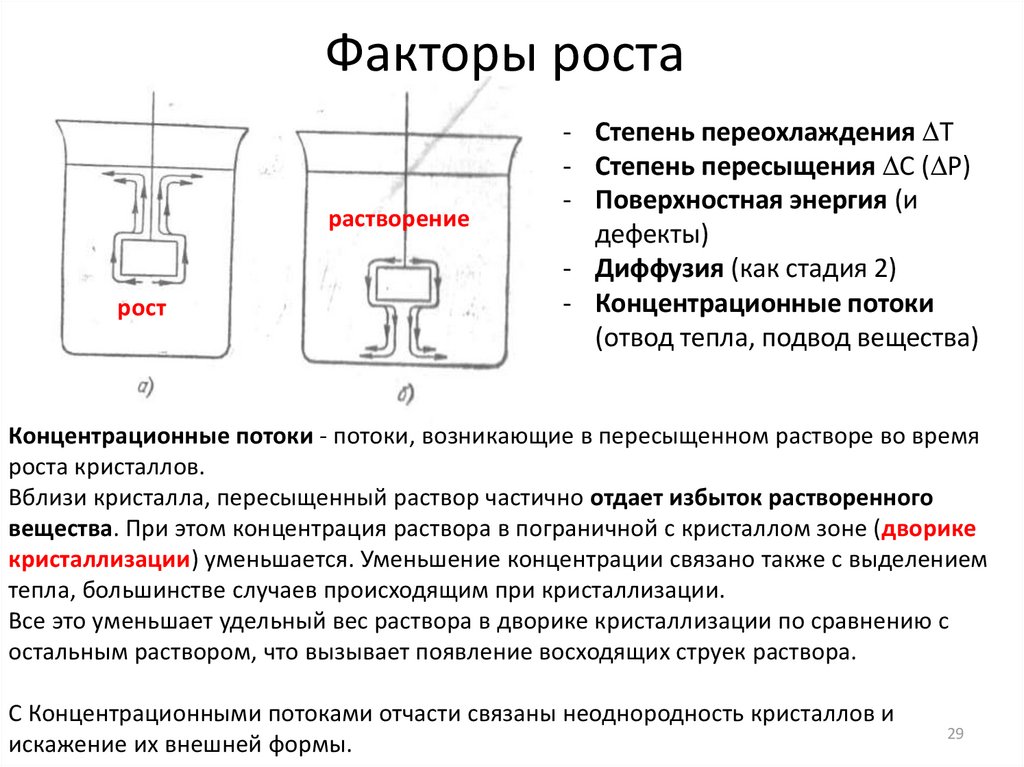
Факторы роста
растворение
рост
- Степень переохлаждения Т
- Степень пересыщения С ( Р)
- Поверхностная энергия (и
дефекты)
- Диффузия (как стадия 2)
- Концентрационные потоки
(отвод тепла, подвод вещества)
Концентрационные потоки - потоки, возникающие в пересыщенном растворе во время
роста кристаллов.
Вблизи кристалла, пересыщенный раствор частично отдает избыток растворенного
вещества. При этом концентрация раствора в пограничной с кристаллом зоне (дворике
кристаллизации) уменьшается. Уменьшение концентрации связано также с выделением
тепла, большинстве случаев происходящим при кристаллизации.
Все это уменьшает удельный вес раствора в дворике кристаллизации по сравнению с
остальным раствором, что вызывает появление восходящих струек раствора.
С Концентрационными потоками отчасти связаны неоднородность кристаллов и
искажение их внешней формы.
29

30.

Теория роста кристаллов Гиббса-Кюри-Вульфа
Кристалл принимает такую совместимую с его симметрией
форму, при которой его свободная поверхностная энергия
минимальна.
1) Гиббс: кристалл растет не плавно, а скачкообразно, слой за
слоем.
2) Кюри и Вульф: скорости роста граней (в направлении
нормали к ним) пропорциональны удельным поверхностным
энергиям граней.
3) Вульф: (как и Браве): скорость роста грани зависит от
ретикулярной плотности. Кристалл покрывается медленно
растущими гранями, а быстро растущие исчезают.
4) Шубников: чем ниже степень пересыщения, тем более
кристалл становится похож на шар и тем больше у него граней.
30

31.

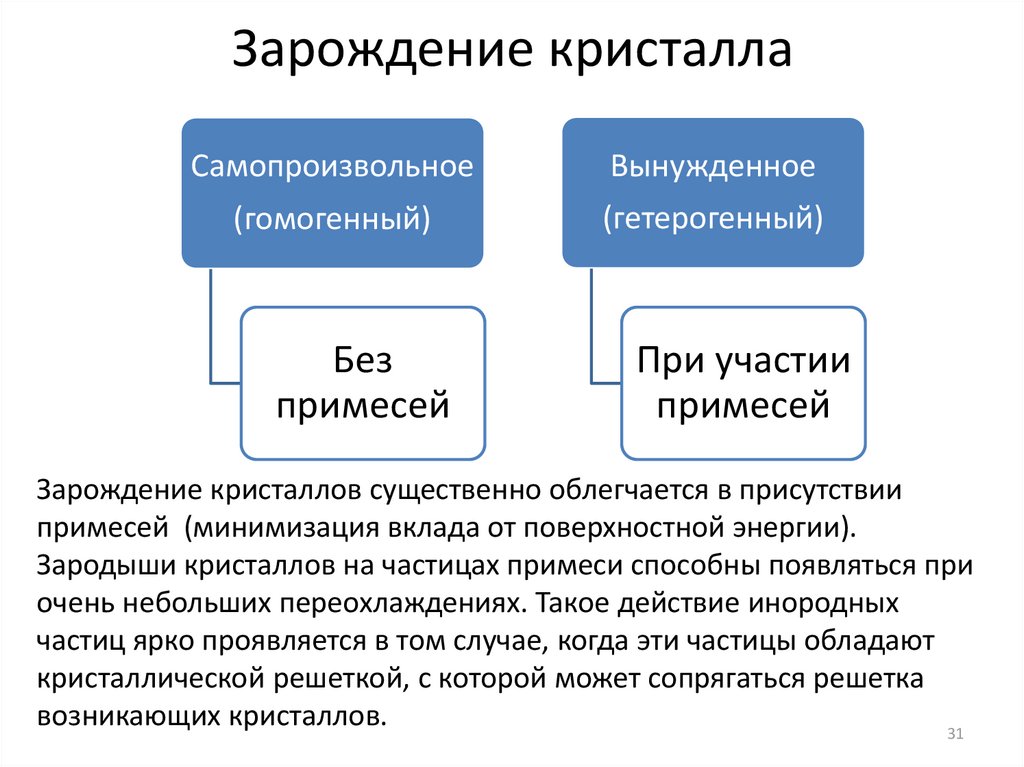
Зарождение кристалла
Самопроизвольное
Вынужденное
(гомогенный)
(гетерогенный)
Без
примесей
При участии
примесей
Зарождение кристаллов существенно облегчается в присутствии
примесей (минимизация вклада от поверхностной энергии).
Зародыши кристаллов на частицах примеси способны появляться при
очень небольших переохлаждениях. Такое действие инородных
частиц ярко проявляется в том случае, когда эти частицы обладают
кристаллической решеткой, с которой может сопрягаться решетка
возникающих кристаллов.
31

32.

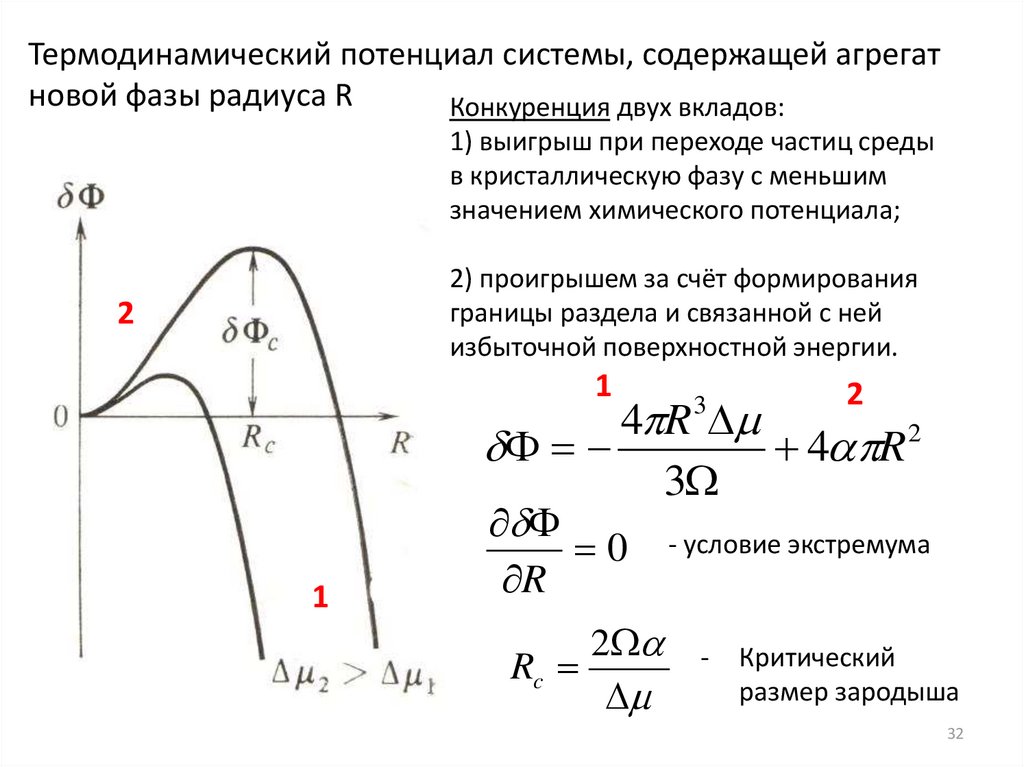
Термодинамический потенциал системы, содержащей агрегат
новой фазы радиуса R
Конкуренция двух вкладов:
1) выигрыш при переходе частиц среды
в кристаллическую фазу с меньшим
значением химического потенциала;
2) проигрышем за счёт формирования
границы раздела и связанной с ней
избыточной поверхностной энергии.
2
1
2
4 R
2
4 R
3
- условие экстремума
1
R
3
0
2
Rc
-
Критический
размер зародыша
32