Similar presentations:
Алгоритмы внешней сортировки данных
1.
ФГОБУ ВПО "СибГУТИ"Кафедра вычислительных систем
ЯЗЫКИ ПРОГРАММИРОВАНИЯ / ПРОГРАММИРОВАНИЕ
Алгоритмы внешней сортировки
(часть I, базовые понятия и алгоритмы)
Преподаватель:
Доцент Кафедры ВС, к.т.н.
Поляков Артем Юрьевич
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
2.
Сортировка данныхСортировка – процесс перестановки элементов некоторого
множества в определенном порядке.
возрастание
3 9 2 8 4 1 7
1 2 3 4 7 8 9
убывание
9 8 7 4 3 2 1
Цель сортировки – упрощение поиска данных в этом
множестве.
Задача сортировки данных часто возникает при разработке
программного обеспечения.
Алгоритмы сортировки можно разделить на:
алгоритмы внутренней сортировки;
алгоритмы внешней сортировки.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
2
3.
Оценка алгоритмов сортировки (1)Время (вычислительная сложность) – основной
параметр, характеризующий быстродействие алгоритма.
При анализе алгоритмов обычно учитывают худшее,
среднее и лучшее поведение алгоритма на наборе
допустимых входных данных размера n (n – мощность
входного множества A: n = |A|).
Для типичного алгоритма сортировки хорошее поведение
– это O(n∙log n) и плохое поведение — это O(n2).
При оценке алгоритмов сортировки учитывается:
С – количество операций сравнения;
М – количество операций пересылки данных.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
3
4.
Оценка алгоритмов сортировки (2)Память – ряд алгоритмов требует выделения
дополнительной памяти под временное хранение данных.
При оценке не учитывается:
место, которое занимает исходный массив
независящие от входной последовательности затраты,
например, на хранение кода программы. Считается, что
такие расходы требуют O(1) памяти.
Алгоритмы
сортировки,
не
потребляющие
дополнительной памяти, относят к сортировкам на месте.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
4
5.
Алгоритмы внешней ивнутренней сортировки
Алгоритмы внутренней сортировки
оперируют сравнительно
небольшими объемами данных.
Они могут "видеть" любой элемент
сортируемого множества
Алгоритмы внешней сортировки
применяются тогда, когда
количество элементов велико и нет
возможности "разложить их на
столе" (в оперативной памяти).
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
5
6.
Алгоритмы внутренней сортировкиАлгоритмы внутренней сортировки (сортировки массивов)
предназначены для работы с данными, которые полностью
помещаются в оперативную память вычислительной
машины, выполняющей данную операцию.
Для оперативной памяти характерно приблизительно
одинаковое время доступа ко всем ее элементам.
Поэтому важной характеристикой алгоритмов внутренней
сортировки является экономичность по памяти.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
6
7.
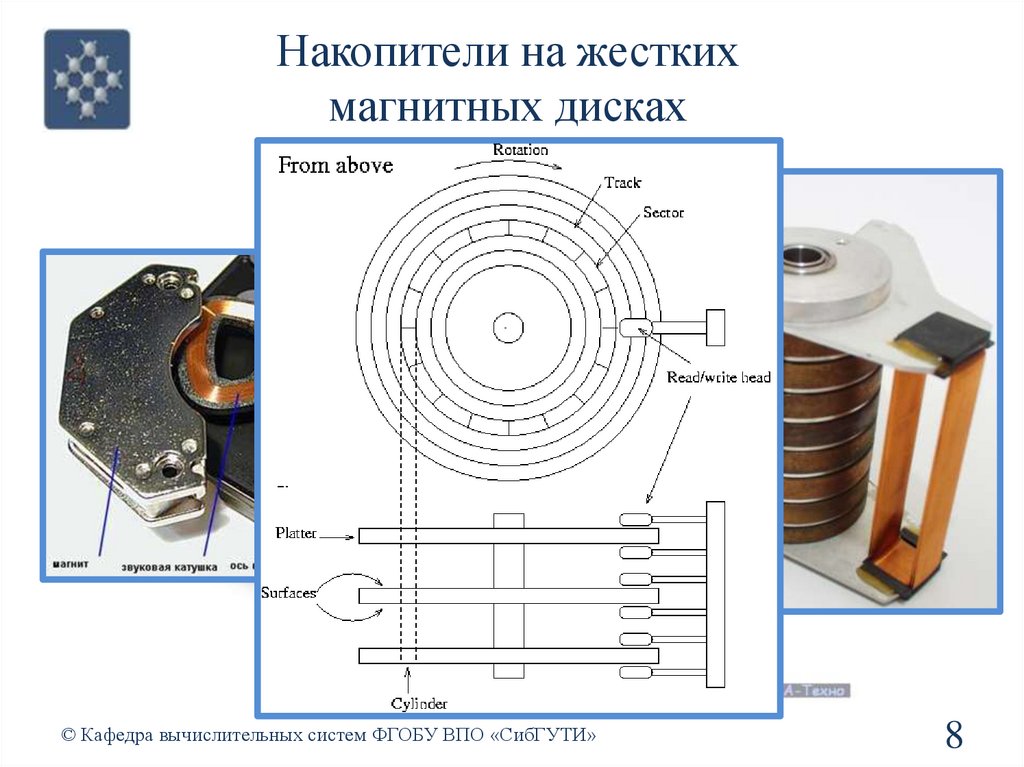
Алгоритмы внешней сортировкиАлгоритмы внешней сортировки (сортировки файлов)
предназначены для работы с данными, объем которых не
позволяет полностью разместить их в оперативной памяти
вычислительной машины, выполняющей данную операцию.
Входные данные располагаются на внешних запоминающих
устройствах, таких как диски и магнитные ленты.
Внешняя память характеризуется последовательным
доступом к ее элементам. В каждый момент времени
имеется непосредственный доступ только к одному
элементу.
Основной метод сортировки – слияние.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
7
8.
Накопители на жесткихмагнитных дисках
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
8
9.
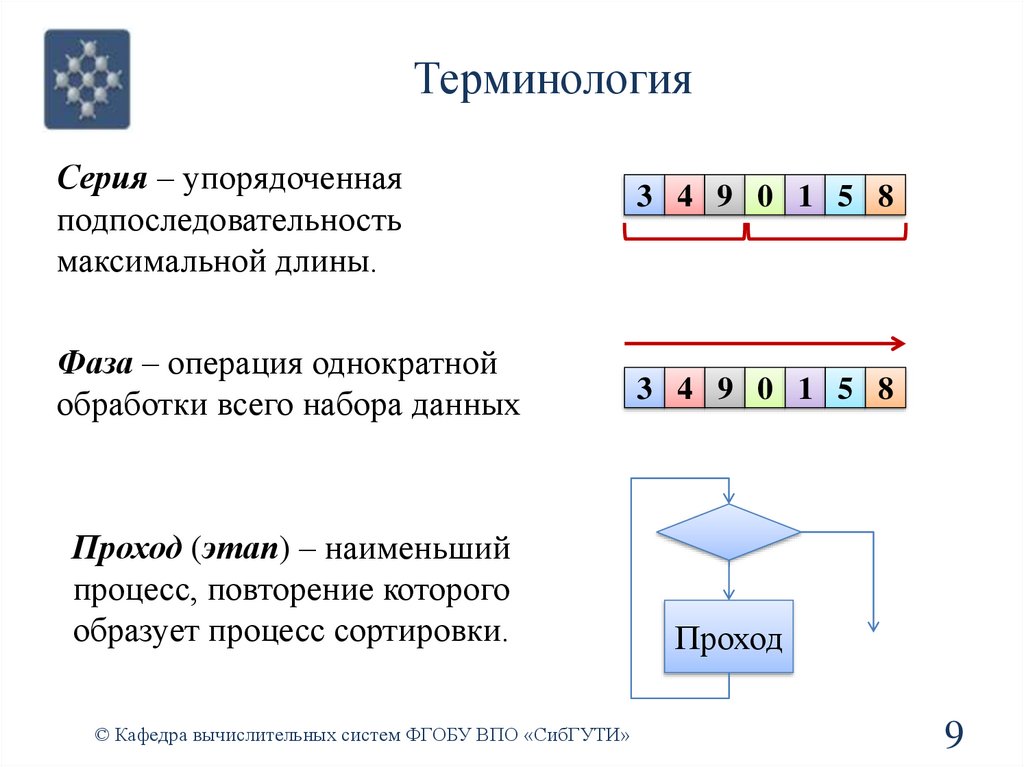
ТерминологияСерия – упорядоченная
подпоследовательность
максимальной длины.
Фаза – операция однократной
обработки всего набора данных
Проход (этап) – наименьший
процесс, повторение которого
образует процесс сортировки.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
3 4 9 0 1 5 8
3 4 9 0 1 5 8
Проход
9
10.
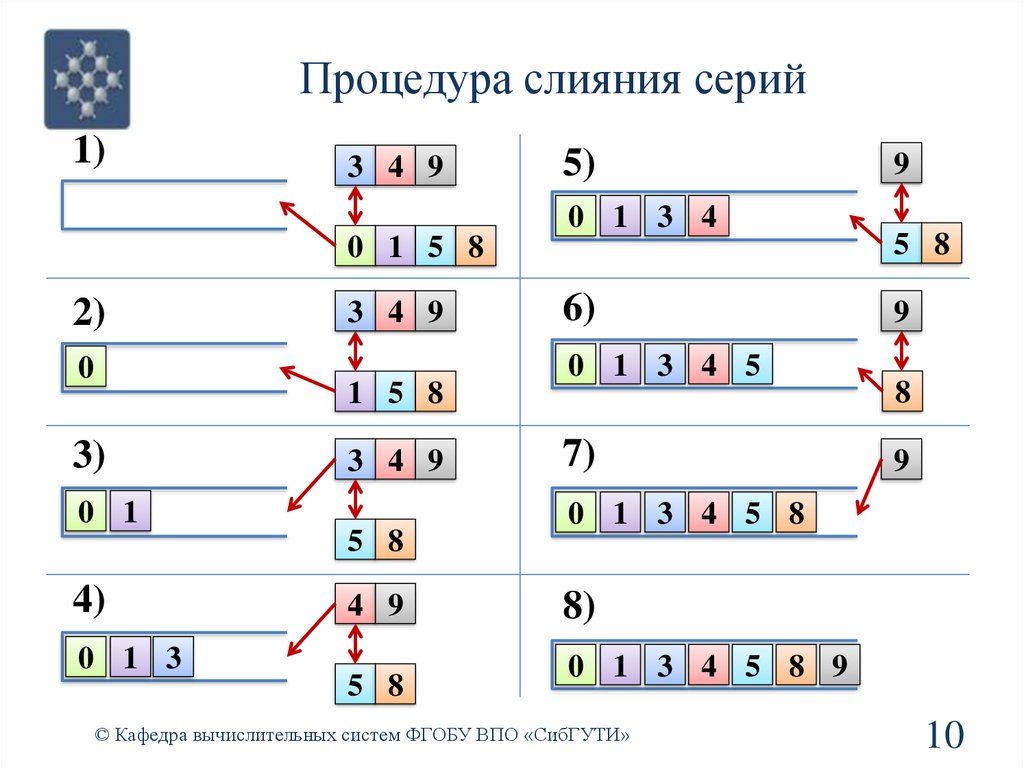
Процедура слияния серий1)
3 4 9
5)
0 1 3 4
0 1 5 8
2)
0
3 4 9
1 5 8
3)
3 4 9
0 1
5 8
4)
0 1 3
4 9
5 8
6)
0 1 3 4 5
7)
9
5 8
9
8
9
0 1 3 4 5 8
8)
0 1 3 4 5 8 9
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
10
11.
Процедура слияния (2)3 4 9
0 1 5 8
7 8 8 8 9
...
1 2 3 4
5 7 7 8 9
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
11
12.
ЗаданиеВыполнить слияние следующих последовательностей:
4 1 8 4 12 43 19 21
9 10 11 4 3 22 17
7 12 3 33 21 15 32 8
10 9 8 12 13 14 15
Слияние выполнять отдельно по сериям
Сколько серий в полученной последовательности?
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
12
13.
ЗаданиеВыполнить слияние следующих последовательностей:
4 1 8 4 12 43 19 21
9 10 11 4 3 22 17
7 12 3 33 21 15 32 8
10 9 8 12 13 14 15
4 7 9 10 10 11 12 ' 1 3 4 8 9 33 '
3 4 12 12 13 14 15 21 22 43 ' 15 17 19 21 32 ' 8
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
13
14.
ПРОСТАЯ СОРТИРОВКА СЛИЯНИЕМ(STRAIGHT MERGE)
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
14
15.
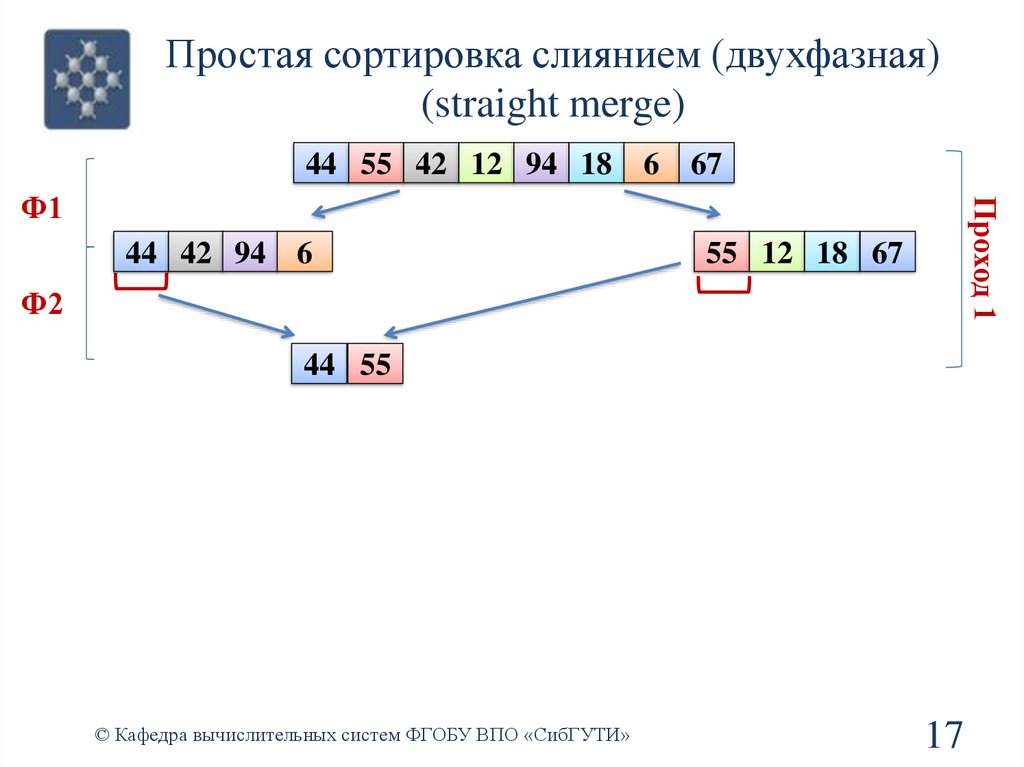
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
6
67
15
16.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
Проход 1
Ф1
55 12 18 67
16
17.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
17
18.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55 12 42
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
18
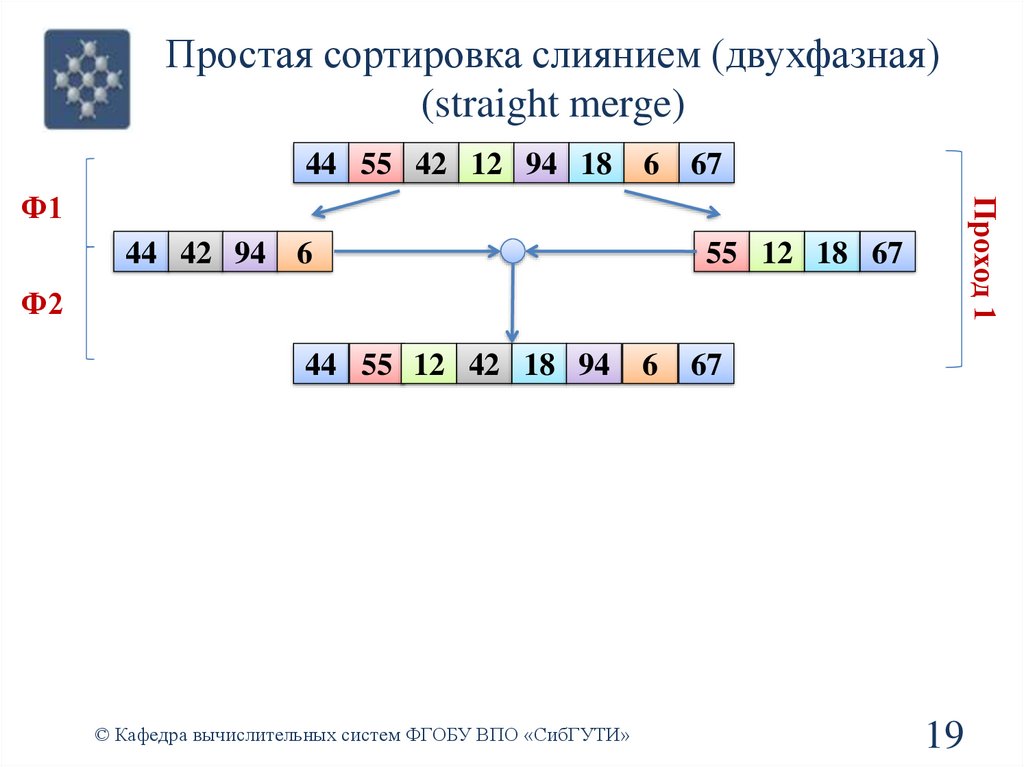
19.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55 12 42 18 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
6
67
19
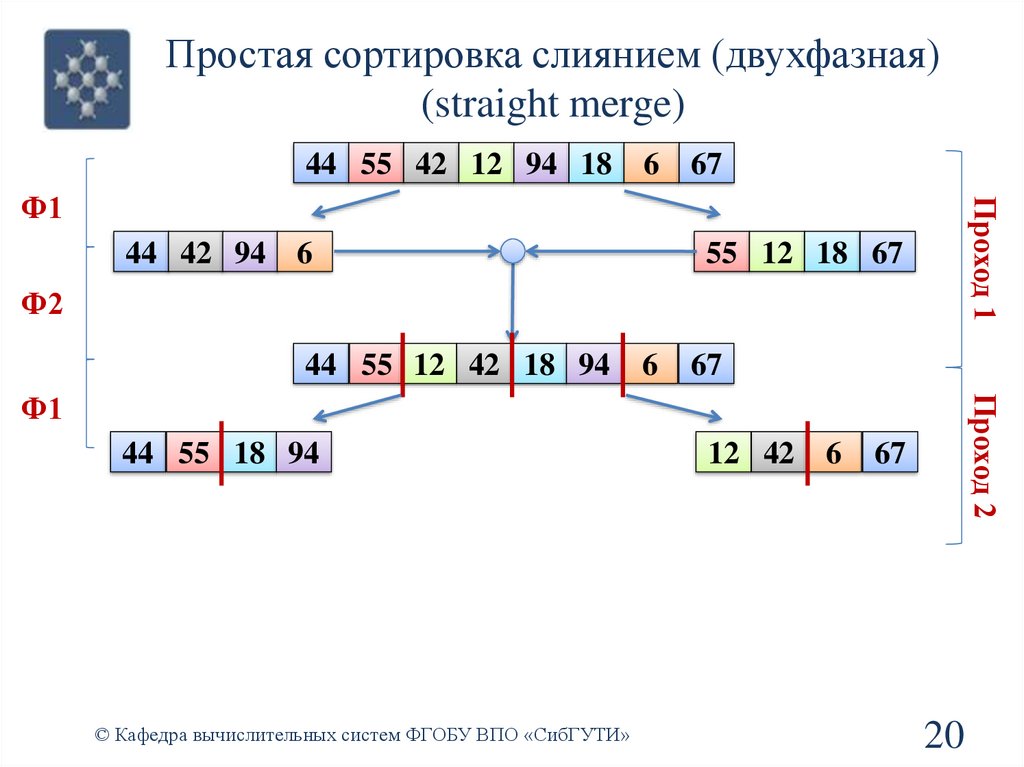
20.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55 12 42 18 94
6
67
44 55 18 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
12 42
6
Проход 2
Ф1
67
20
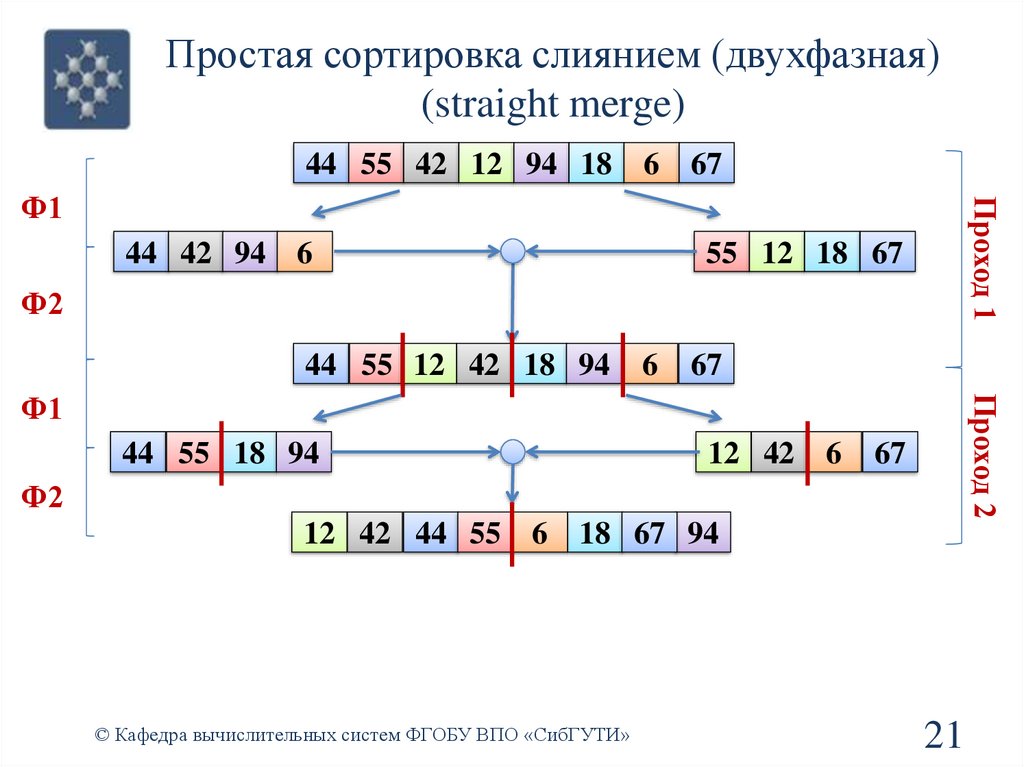
21.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55 12 42 18 94
6
67
44 55 18 94
12 42
6
Проход 2
Ф1
67
Ф2
12 42 44 55 6
18 67 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
21
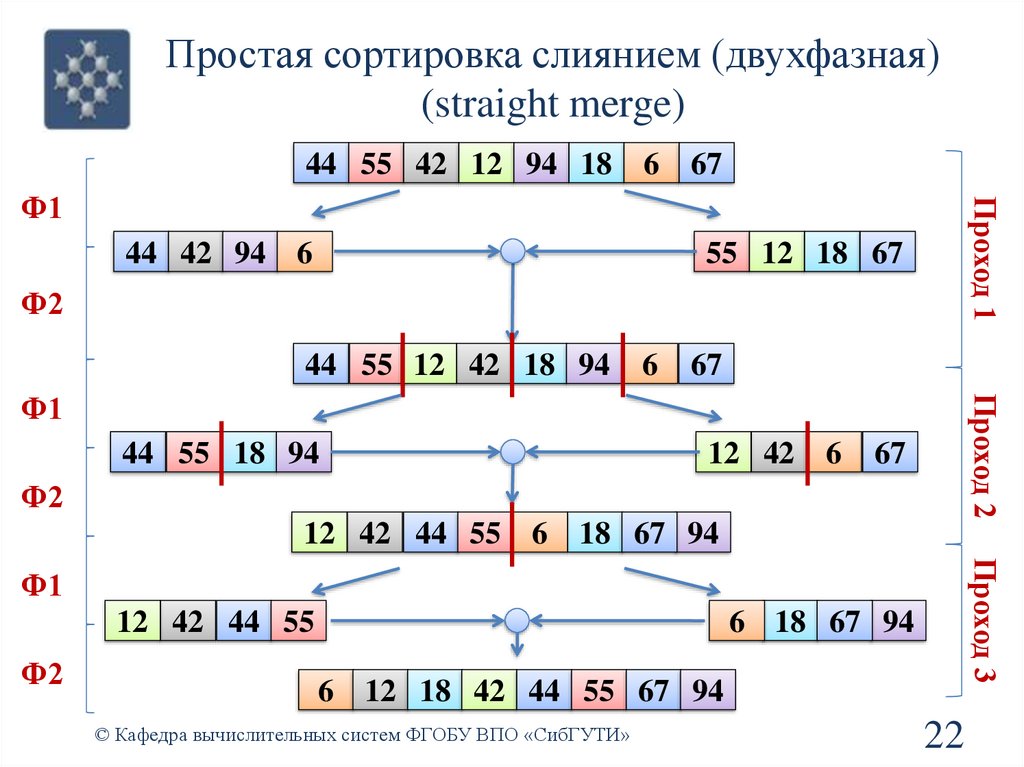
22.
Простая сортировка слиянием (двухфазная)(straight merge)
44 55 42 12 94 18
6
67
44 42 94 6
Проход 1
Ф1
55 12 18 67
Ф2
44 55 12 42 18 94
6
67
44 55 18 94
12 42
6
Проход 2
Ф1
67
Ф2
12 42 44 55 6
18 67 94
Проход 3
Ф1
12 42 44 55
Ф2
6 18 67 94
6 12 18 42 44 55 67 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
22
23.
Алгоритмпростой сортировки слиянием
ввод n, a
k←1
while k < n do
(b, c) ← DISTR(a, n, k)
a ← MERGE(b, c, k)
k←k∙2
done
MERGE(b, c, k)
while b ≠ < > ИЛИ с ≠ < > do
f1← first(b), b ← rest(b), n1 ← 1
f2← first(c), c ← rest(c), n2 ← 1
while b ≠ < > И с ≠ < > И
n1 ≤ k И n2 ≤ k do
if f1 < f2 then
a ← a & f1, n1 ← n1 + 1
f1← first(b), b ← rest(b)
DISTRIBUTE(a, n, k)
else
i ← 1, b ← < >, c ← < >
a ← a & f 2, n 2 ← n 2 + 1
while i < n do
f2← first(c), c ← rest(c)
k ← min(n – i, k)
while b ≠ < > И n1 ≤ k do n1 ← n1 + 1,
b ← b & <ai, …, ai+k >
a ← a & first (b), b ← rest(b)
b↔c
while с ≠ < > И n2 ≤ k do n2 ← n2 + 1,
i←i+k
a ← a & first (с) , c ← rest(c)
return (b, c)
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
23
24.
Реализация алгоритма распределенияvoid distr(int s[], int n, int d1[], int *d1n,
DISTRIBUTE(a, n, k)
int d2[], int *d2n, int k)
i ← 1, b ← < >, c ← < >
{
while i < n do
int *wptr = d1, *bptr = d2, *tp;
k ← min(n – i, k)
int *wn = d1n, *bn = d2n, i = 0, j, *tn;
b ← b & <ai, …, ai+k >
*wn = 0; *bn = 0;
b↔c
while( i < n ){
i←i+k
k = (k < (n - i)) ? k : n - i; // min(k,n-i)
return (b, c)
for(j=0; j<k; j++){
wptr[(*wn)++] = s[i++];
}
tp = wptr; wptr = bptr; bptr = tp;
tn = wn; wn = bn; bn = tn;
}
}
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
24
25.
Алгоритмпростой сортировки слиянием
ввод n, a
k←1
while k < n do
(b, c) ← DISTR(a)
a ← MERGE(b, c)
k←k∙2
done
Выполнить сортировку последовательности:
91 4 18 26 44 21 30 19 81 16 45 200 57 71 82 99 150 212
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
25
26.
Анализ алгоритмапростой сортировки слиянием
ввод n, a
k←1
while k < n do
(b, c) ← DISTR(a)
a ← MERGE(b, c)
k←k∙2
done
Количество R пересылок
данных на одном этапе:
этап состоит из двух фаз,
на
каждой
из
которых
выполняется
копирование
всех элементов из a;
Количество R элементов,
обраб. на одном этапе:
6 12 44 94 18 42 55 67
6 12 44 94
R = 2n
18 42 55 67
6 12 18 42 44 55 67 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
26
27.
Анализ алгоритмапростой сортировки слиянием
Количество i этапов:
зависит от параметра k
(длина серии), который на
каждом этапе удваивается;
общее число i этапов:
ввод n, a
k←1
while k < n do
(b, c) ← DISTR(a)
a ← MERGE(b, c)
k←k∙2
done
44 55 12 42 94 18
44 94 18 55 6
i = [log2n] + 1
6
67
12 42 67
6 12 44 94 18 42 55 67
6 12 18 42 44 55 67 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
1) k = 1 (20)
2) k = 2 (21)
3) k = 4 (22)
i) k = 2i – 1 < n
i+1) k = 2i ≥ n
27
28.
Анализ алгоритмапростой сортировки слиянием
ввод n, a
k←1
while k < n do
(b, c) ← DISTR(a)
a ← MERGE(b, c)
k←k∙2
done
Количество M пересылок:
M = i ∙ R = 2n∙[log2 n] =
O(n∙log2 n)
Число C сравнений по ключу:
сопоставимо с M;
время сравнения значительно ниже времени пересылки.
Алгоритм требует n = O(n) дополнительной памяти
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
28
29.
Недостатки алгоритмапростой сортировки слиянием
Доступ к данным на внешнем устройстве занимает
существенное время
Фаза разбиения последовательности по
вспомогательным файлам не вносит вклада в
сортировку (переупорядочивания элементов не
происходит)
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
29
30.
МЕТОД СБАЛАНСИРОВАННЫХСЛИЯНИЙ
(BALANCED MERGE)
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
30
31.
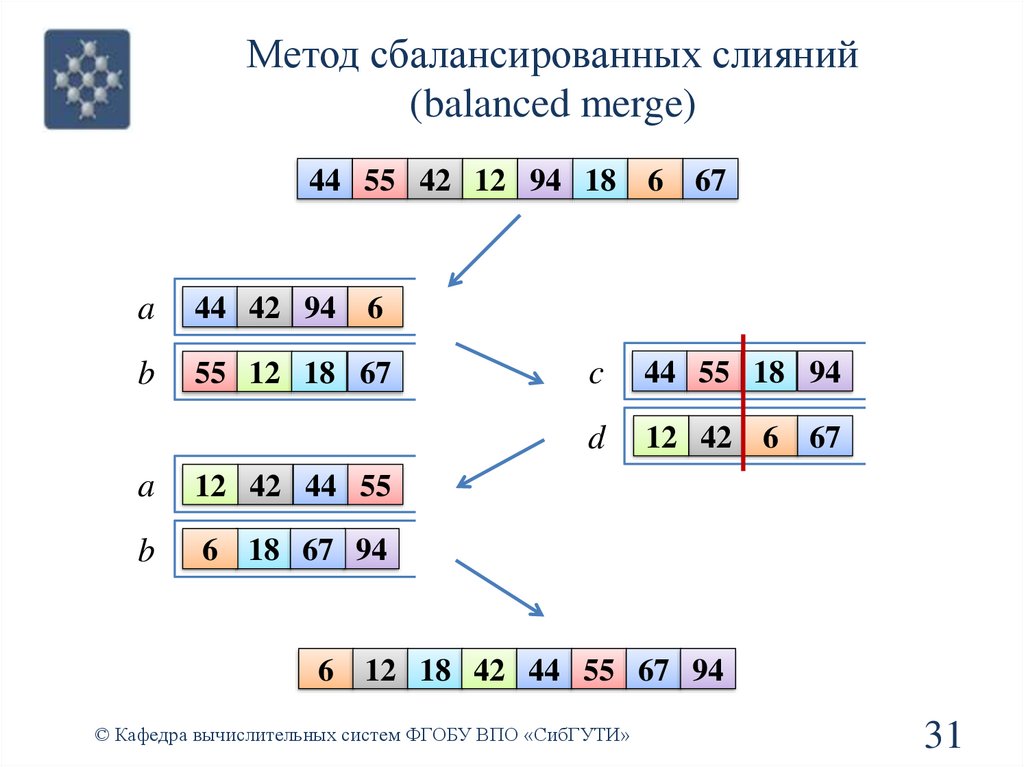
Метод сбалансированных слияний(balanced merge)
44 55 42 12 94 18
a
44 42 94
b
55 12 18 67
6
67
6
a
12 42 44 55
b
6 18 67 94
c
44 55 18 94
d
12 42 6 67
6 12 18 42 44 55 67 94
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
31
32.
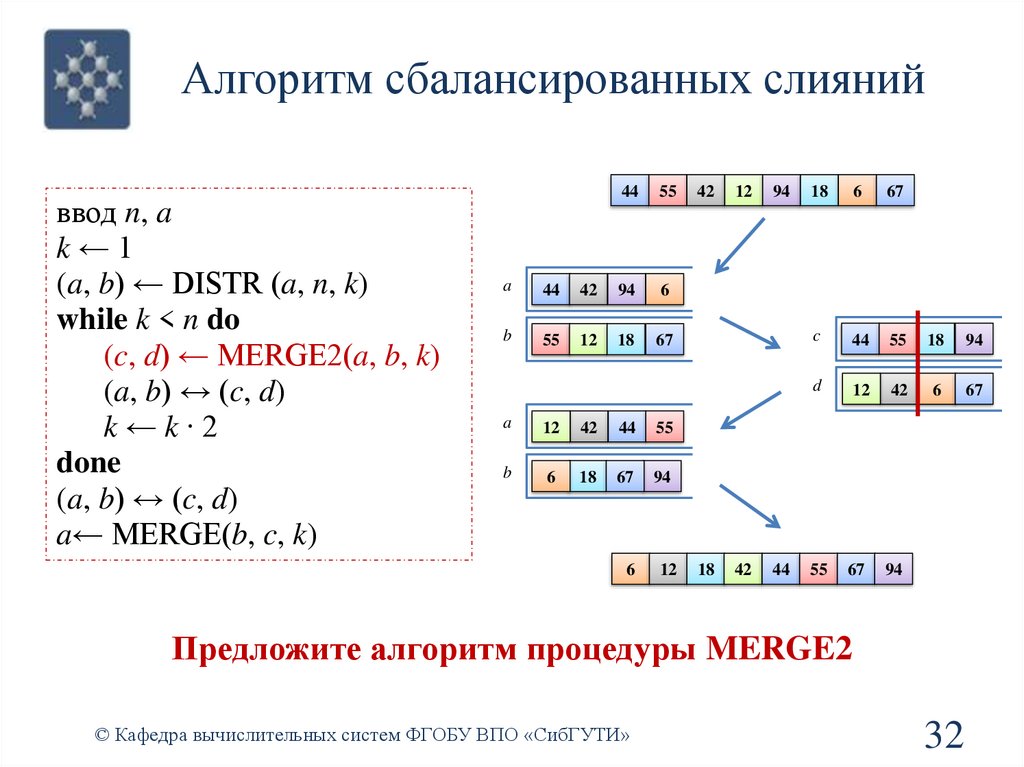
Алгоритм сбалансированных слиянийввод n, a
k←1
(a, b) ← DISTR (a, n, k)
while k < n do
(c, d) ← MERGE2(a, b, k)
(a, b) ↔ (c, d)
k←k∙2
done
(a, b) ↔ (c, d)
a← MERGE(b, c, k)
44
55
a
44
42
94
6
b
55
12
18
67
a
12
42
44
55
b
6
18
67
94
6
12
42
18
12
42
94
44
18
6
67
c
44
55
18
94
d
12
42
6
67
55
67
94
Предложите алгоритм процедуры MERGE2
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
32
33.
Объединенная процедураслияния и распределения
MERGE2(s1, s2, k)
d1 ← < >, d2 ← < >, f1← first(s1), f2← first(s2),
s1 ← rest(s1), s2 ← rest(s2)
while s1 ≠ < > ИЛИ s2 ≠ < > do
n1 ← 1, n2 ← 1
while (s1 ≠ < > И n1 ≤ k) И (s2 ≠ < > И n2 ≤ k) do
if f1 < f2 then d1 ← d1 & f1 , n1 ← n1 + 1,
f1 ← first(s1) , s1 ← rest(s1)
else d1 ← d1 & f2, n2 ← n2 + 1,
f2 ← first(s2) , s2 ← rest(s2)
while s1 ≠ < > И n1 ≤ k do
d1 ← d1 & first (s1)
while s2 ≠ < > И n2 ≤ k do
d1 ← d1 & first (s2)
d2 ↔ d1
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
a
44
42
94
6
b
55
12
18
67
c
44
55
18
94
d
12
42
6
67
33
34.
Анализ алгоритмасбалансированной сортировки слиянием
ввод n, a
k←1
(a, b) ← DISTR(a, n, k)
while k < n do
(c, d) ← MERGE2(a, b, k)
(a, b) ↔ (c, d)
k←k∙2
done
(a, b) ↔ (c, d)
a← MERGE(b, c, k)
Оцените количество пересылок данных, которое
производится при применении алгоритма
сбалансированной сортировки слиянием
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
34
35.
Анализ алгоритмасбалансированной сортировки слиянием
ввод n, a
k←1
(a, b) ← DISTR(a, n, k)
while k < n do
(c, d) ← MERGE2(a, b, k)
(a, b) ↔ (c, d)
k←k∙2
done
(a, b) ↔ (c, d)
a← MERGE(b, c, k)
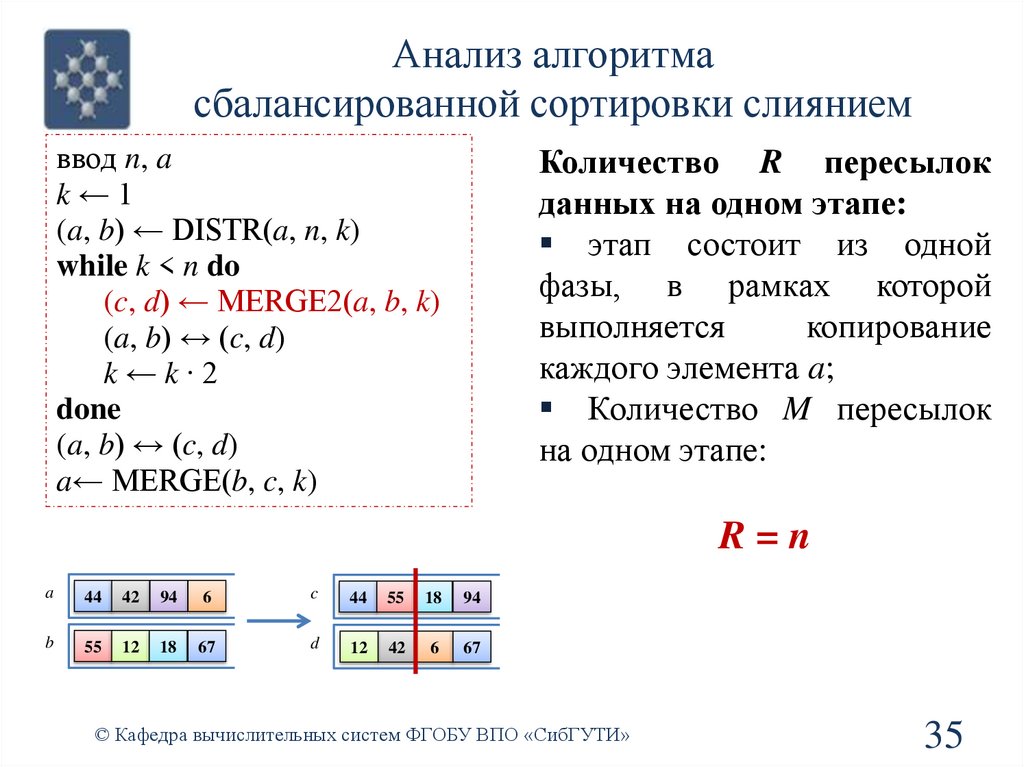
Количество R пересылок
данных на одном этапе:
этап состоит из одной
фазы, в рамках которой
выполняется
копирование
каждого элемента a;
Количество M пересылок
на одном этапе:
R=n
a
44
42
94
6
c
44
55
18
94
b
55
12
18
67
d
12
42
6
67
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
35
36.
Анализ алгоритмасбалансированной сортировки слиянием
ввод n, a
k←1
(a, b) ← DISTR(a, n, k)
while k < n do
(c, d) ← MERGE2(a, b, k)
(a, b) ↔ (c, d)
k←k∙2
done
(a, b) ↔ (c, d)
a← MERGE(b, c, k)
44
42
94
6
55
12
18
67
Количество i этапов:
зависит от параметра k
(длина серии), который на
каждом этапе удваивается;
общее число i этапов:
i = [log2n] + 1
1) k = 1 (20)
2) k = 2 (21)
3) k = 4 (22)
I
44
55
18
94
II
12
42
44
55
6
18
67
94
12
42
6
67
III
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
i) k = 2i – 1 < n
i+1) k = 2i ≥ n
36
37.
Анализ алгоритмасбалансированной сортировки слиянием
ввод n, a
k←1
(a, b) ← DISTR(a, n, k)
while k < n do
(c, d) ← MERGE2(a, b, k)
(a, b) ↔ (c, d)
k←k∙2
done
(a, b) ↔ (c, d)
a← MERGE(b, c, k)
Количество M пересылок:
M = i ∙ R = n∙[log2 n] =
O(n∙log2 n)
Число C сравнений по ключу:
сопоставимо с M;
время сравнения значительно ниже времени пересылки.
Алгоритм требует 2n = O(n) дополнительной памяти
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
37
38.
Недостатки алгоритмовпростой и сбалансированной
сортировки слиянием
Доступ к данным на внешнем устройстве занимает
существенное время
Рассмотренные алгоритмы сортировки не обладают
свойством естественности поведения.
Естественность поведения –
эффективность метода при обработке уже
упорядоченных или частично упорядоченных данных.
Алгоритм ведёт себя естественно, если учитывает эту
характеристику входной последовательности и работает
лучше.
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
38
39.
Литература1. Вирт Н. Алгоритмы и структуры данных. Новая версия
для Оберона / Пер. с англ. Ткачев Ф.В. – М.: ДМК Пресс,
2012 г. – 272 с.,
2. Кнут, Д.Э. Искусство программирования: в 3 т. Т. 3.
Сортировка и поиск [Текст] : [учеб. пособие]; пер. с англ. /
под общ. ред. Ю.В. Казаченко. - 3-е изд. – М.: Издат.дом
"Вильямс", 2010. – 822с.
3. Седжвик Р. Алгоритмы на C++ (Algorithms in C++): Пер. с
англ. – М.: Издательский дом "Вильямс", 2011 г. – 1056 c. –
ISBN 978-5-8459-1650-1, 978-0-321-60633-4;
© Кафедра вычислительных систем ФГОБУ ВПО «СибГУТИ»
39




























 programming
programming








