Транспортные сети. (Лекция 15)

1.

Компьютерная дискретная математика
Транспортные сети
Лекция 15
Н.В. Белоус
Факультет компьютерных наук
Кафедра ПО ЭВМ, ХНУРЭ
ХНУРЭ,
кафедра
ПО
[email protected]
ЭВМ,
Тел.
7021-446,
e-mail:

2. Основные определения

Сеть – это связный ориентированный граф без петель,
в котором:
1. Имеется только одна вершина (узел), в которую не
заходит ни одна дуга, называемая входом (истоком) x0
2. Имеется только одна, вершина (узел), из которой не
выходит ни одна дуга, называемая выходом (стоком) z
3. Каждой дуге u присвоена числовая характеристика
C(u) 0, которая называется пропускной способностью
дуги u
2

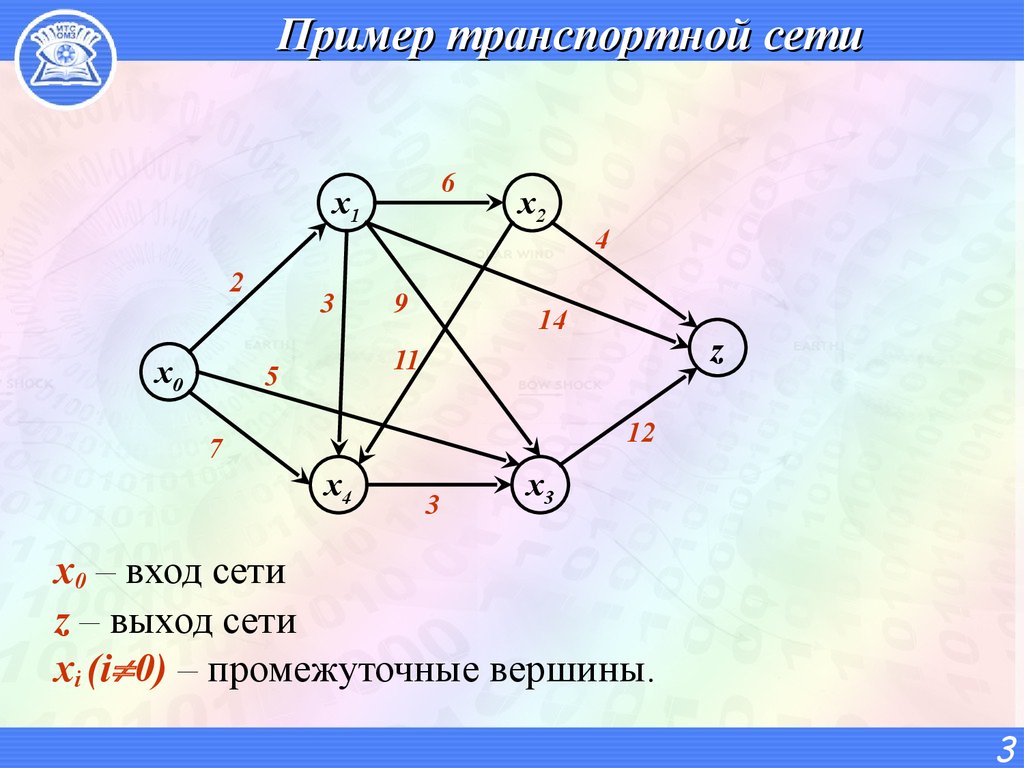
3. Пример транспортной сети

6
x1
2
x0
3
9
x2
4
14
z
11
5
12
7
x4
3
x3
x0 – вход сети
z – выход сети
xi (i 0) – промежуточные вершины.
3

4. Поток сети

Потоком на транспортной сети называется функция
(u), заданная на множестве дуг сети, которое
удовлетворяет свойствам:
1)
0 ( u ) C( u )
2)
( u ) (.u )
u U x
u U x
( U ) ( U )
u U x 0
u U z
z
U x множество дуг, входящих в вершину х
U x множество дуг, выходящих из вершины х
z поток в транспортной сети
4

5. Основные определения

Дуга u
(u)=C(u)
называется
насыщенной,
если
поток
Дуга u называется свободной если (u)=0
Дуга u называется занятой, если (u)>0
Поток в сети называется полным, если любой путь,
идущий от входа к выходу сети содержит хотя бы одну
насыщенную дугу.
5

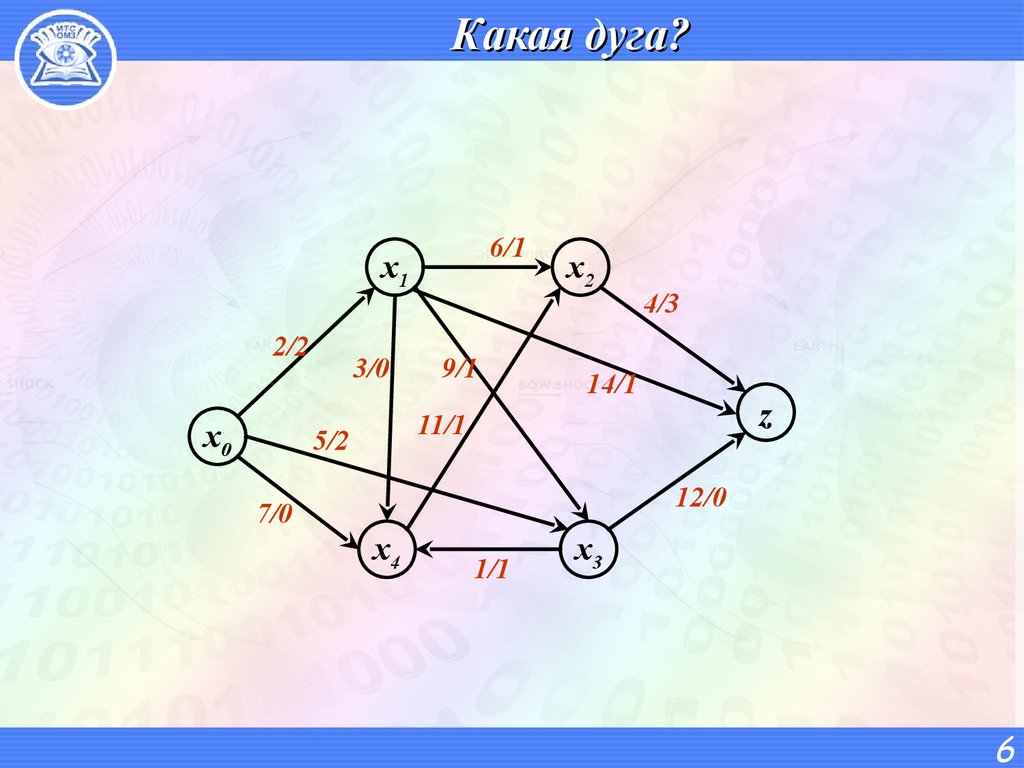
6. Какая дуга?

6/1
x1
2/2
x0
3/0
9/1
x2
4/3
14/1
z
11/1
5/2
12/0
7/0
x4
1/1
x3
6

7. Разрез транспортной сети

Разрезом называется множество дуг, соединяющих
вершины множества
и
. A
A
U A U A U A
(U ) ( U )
u U A
C( A )
u U A
z
C(U )
u U A
A совокупность вершин сети такая, что x0 A а z A.
A совокупность вершин сети такая, что x0 A а z A.
U A множества дуг, входящих в вершины множества А
U A множества дуг, выходящих из вершин множества А
7

8. Пример

x1
x2
z
x0
x4
x3
A { x3 , z }
A { x0 , x 1 , x 2 , x 4 }
U A {(x0,x3), (x1,x3), (x1,z), (x2,z)}
U A {(x3,x4)}
8

9. Задача о наибольшем потоке в сети

При заданной конфигурации и указанных пропускных
способностях дуг определить максимальный поток,
который можно пропустить через сеть и его
распределение по дугам
9

10. Теорема Форда-Фалкерсона

Если в транспортной сети для некоторого
разреза V и величины потока z имеет место
C(A)= z , то V обладает минимальной пропускной
способностью в сети, а z является максимальным
для данной сети.
10

11. Пример

3/0
x1
1/1
2/1
1/1
x2
2/2
1/1
z
x0
5/2
6/3
x4
3/3
1 x0 x 1 x 2 z
2 x0 x 1 x 4 x 2 z
3 x0 x 1 x 4 x 3 x 2 z
4 x0 x 1 x 4 x 3 z
x3
5 x0 x 4 x 2 z
6 x0 x 4 x 3 x 2 z
7 x0 x 4 x 3 z
z 4
11

12. Алгоритм Форда-Фалкерсона

Алгоритм в основном включает 2 этапа:
1.Нахождение полного потока.
2.Нахождение максимального потока, с помощью
передачи меток.
12

13. 1.Нахождение полного потока

Поочередно рассмотрим все пути между х0 и z и для
каждой дуги выбранного пути найдем разность между
пропускной способностью дуги и потоком, проходящим по
дуге.
Увеличим поток таким образом, чтобы путь, ведущий из
х0 в z содержал хотя бы одну насыщенную дугу.
Для каждой дуги выбранного пути прибавляем к
числителю минимальную полученную разность ∆.
Выбираем следующий путь. Повторяем эти действия до
тех пор, пока не получим полный поток в сети.
13

14. 2.Нахождение максимального потока, с помощью передачи меток

Увеличение потока z сети состоит в разметке
вершин индексами, указывающими путь, по
которому возможно изменение потока. Если
разметка достигает вершины z, то поток можно
увеличить по пути, соответствующему полученной
разметке.
Увеличение потока возможно до тех пор, пока в
результате разметки вершина z получает метки.
14

15. 2.Нахождение максимального потока, с помощью передачи меток

Шаг 1. Помечаем вершину х0 индексом
Шаг 2. Если xi уже имеет пометку, то:
0
Метка приписывается всем непомеченным вершинам, которые связаны с xi ненасыщенной
дугой, ведущей
+i из xi к данной вершине. Метку получают все вершины y, удовлетворяющие
условиям:
y – непомеченная
Метку получают все непомеченные вершины, связанные занятой дугой, идущей из данной
вершины в вершину xi . Метку получают все вершины y, удовлетворяющие условиям:
( xi , y ) U , ( xi , y ) C ( xi , y )
-i
у – непомеченная
( y , xi ) U , ( xi , y ) 0
15

16. 2.Нахождение максимального потока, с помощью передачи меток (продолжение)

Шаг 3. Если в результате такой разметки окажется
помеченная вершина z, то переходим к пункту 4. В
противном случае, поток, полученный на предыдущем
цикле, был максимальным.
Шаг 4. Строим путь от х0 к z, все вершины которого
соответствуют номерам меток предыдущих вершин с
точностью до знака. Построение пути начинается от
вершины z. Поток во всех дугах пути изменяется по
следующим правилам:
( u ), если u
если направление дуги u и направление потока в сети
( u ) ( u ) 1 ,совпадают
( u ) 1 ,если дуга u и направление потока противоположны
z z 1
16

17. Пример нахождения максимального потока и минимального разреза сети

Для заданной транспортной
сети найдем максимальный
поток и минимальный разрез
при
помощи
алгоритма
Форда-Фалкерсона
10/7
5/2
x0
Находим путь, по которому
возможно увеличение потока
z 12
x2
3/2
10/8
10/7
x0
7/6
7/6
x4
1/0
z
3/0
16/11
x3
z 11
Вычисляем ∆
∆=1
Увеличиваем поток
Величина потока в сети:
2/1
11/9
Величина начального потока в сети:
1 x0 , x 1 , x 4 , z
x1
5/2
x1
2/1
x2
11/9
3/2
7/7
7/6
7/6
x4
1/1
1/0
z
3/0
16/11
x3
17

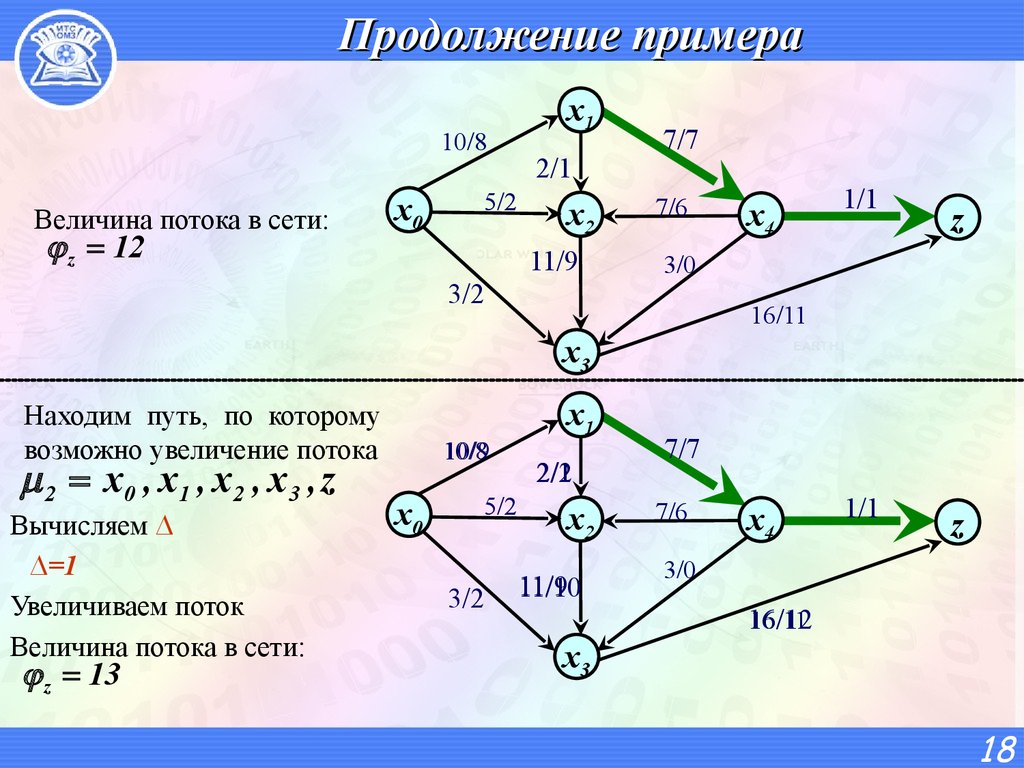
18. Продолжение примера

10/8
Величина потока в сети:
z 12
x0
5/2
x1
2/1
x2
11/9
3/2
7/7
7/6
x4
1/1
z
3/0
16/11
x3
Находим путь, по которому
возможно увеличение потока
2 x0 , x1 , x 2 , x 3 , z
Вычисляем ∆
∆=1
Увеличиваем поток
Величина потока в сети:
z 13
10/8
10/9
x0
5/2
3/2
x1
2/1
2/2
x2
11/9
11/10
7/7
7/6
x4
1/1
z
3/0
16/11
16/12
x3
18

19. Продолжение примера

x1
10/9
Величина потока в сети:
z 13
x0
2/2
5/2
x2
11/10
3/2
7/7
7/6
x4
1/1
z
1/1
z
3/0
16/12
x3
Находим путь, по которому
возможно увеличение потока
3 x0 , x 2 , x 3 , z
Вычисляем ∆
∆=1
Увеличиваем поток
Величина потока в сети:
z 14
x1
10/9
x0
2/2
5/3
5/2
3/2
x2
11/11
11/10
7/7
7/6
x4
3/0
16/13
16/12
x3
19

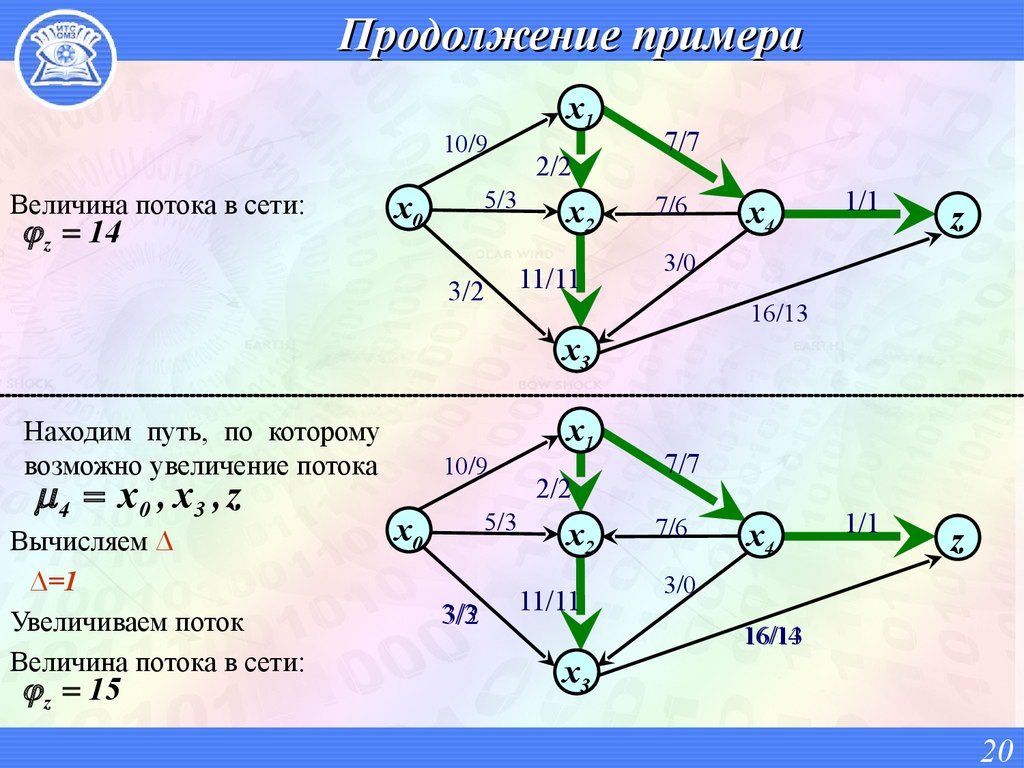
20. Продолжение примера

10/9
Величина потока в сети:
z 14
5/3
x0
3/2
x1
2/2
x2
11/11
7/7
7/6
x4
1/1
z
1/1
z
3/0
16/13
x3
Находим путь, по которому
возможно увеличение потока
4 x0 , x 3 , z
Вычисляем ∆
∆=1
Увеличиваем поток
Величина потока в сети:
z 15
10/9
5/3
x0
3/3
3/2
x1
2/2
x2
11/11
7/7
7/6
x4
3/0
16/14
16/13
x3
20

21. Продолжение примера

0
x0
x1
10/9
2/2
5/3
5/4
x2
+0
7/7
+0
11/11
3/3
-2
7/6
7/5
x4
1/1
+3
z
3/0
3/1
+4
16/14
16/15
x3
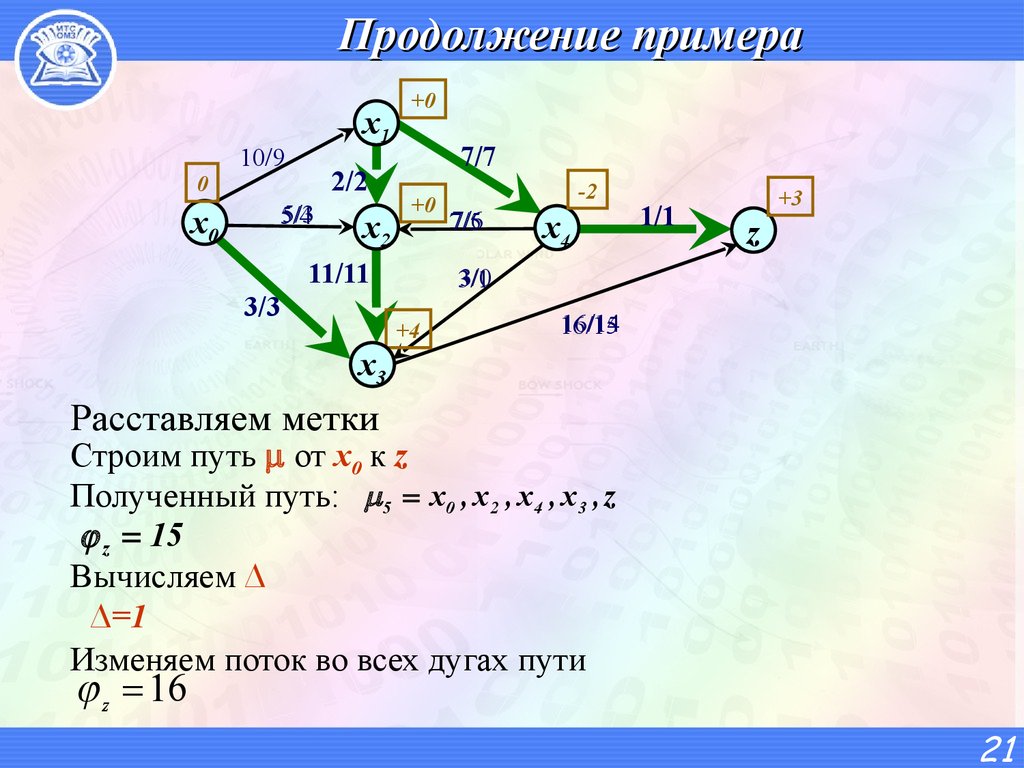
Расставляем метки
Строим путь от х0 к z
Полученный путь: 5 x0 , x 2 , x4 , x 3 , z
z 15
Вычисляем ∆
∆=1
Изменяем поток во всех дугах пути
z 16
21

22. Продолжение примера

0
x1
10/9
2/2
5/5
5/4
x0
x2
+0
7/7
+0
11/11
3/3
-2
7/4
7/5
x4
1/1
+3
z
3/2
3/1
+4
16/16
16/15
x3
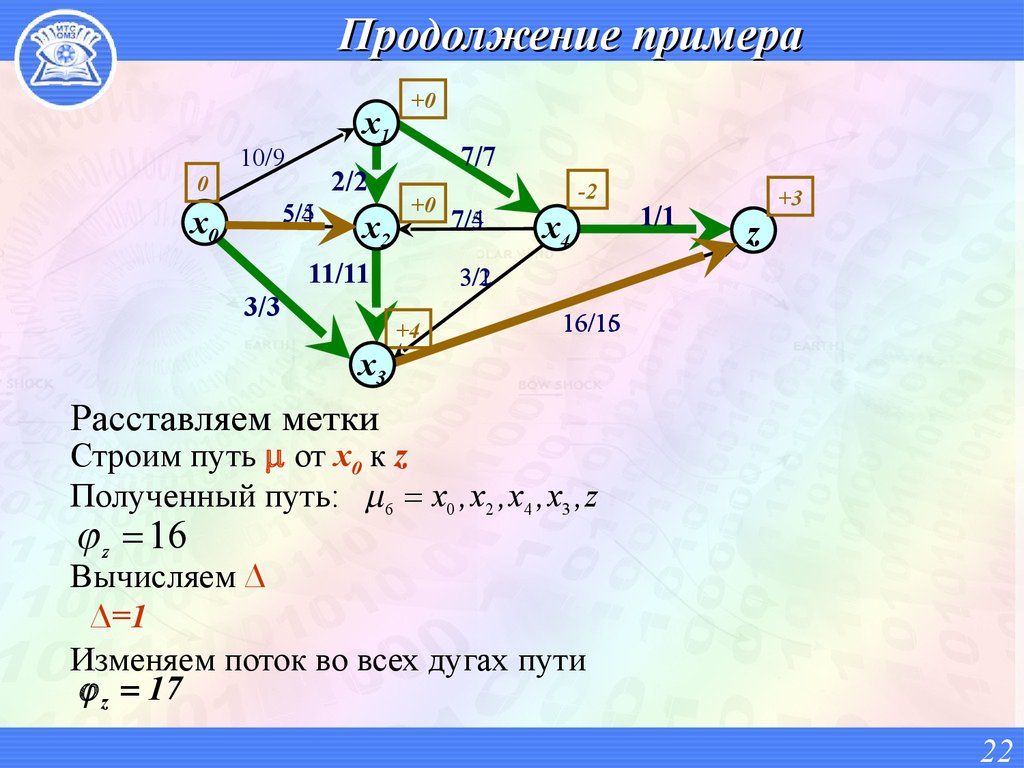
Расставляем метки
Строим путь от х0 к z
Полученный путь: 6 x0 , x2 , x4 , x3 , z
z 16
Вычисляем ∆
∆=1
Изменяем поток во всех дугах пути
z 17
22

23. Продолжение примера

0
x1
10/9
2/2
5/5
x0
x2
+0
7/7
+0
11/11
-2
7/6
x4
1/1
3/2
3/3
16/16
+4
x3
0
x0
10/9
5/5
3/3
x1
+0
2/2
x2
11/11
7/7
7/6
x4
3/2
16/16
x3
1/1
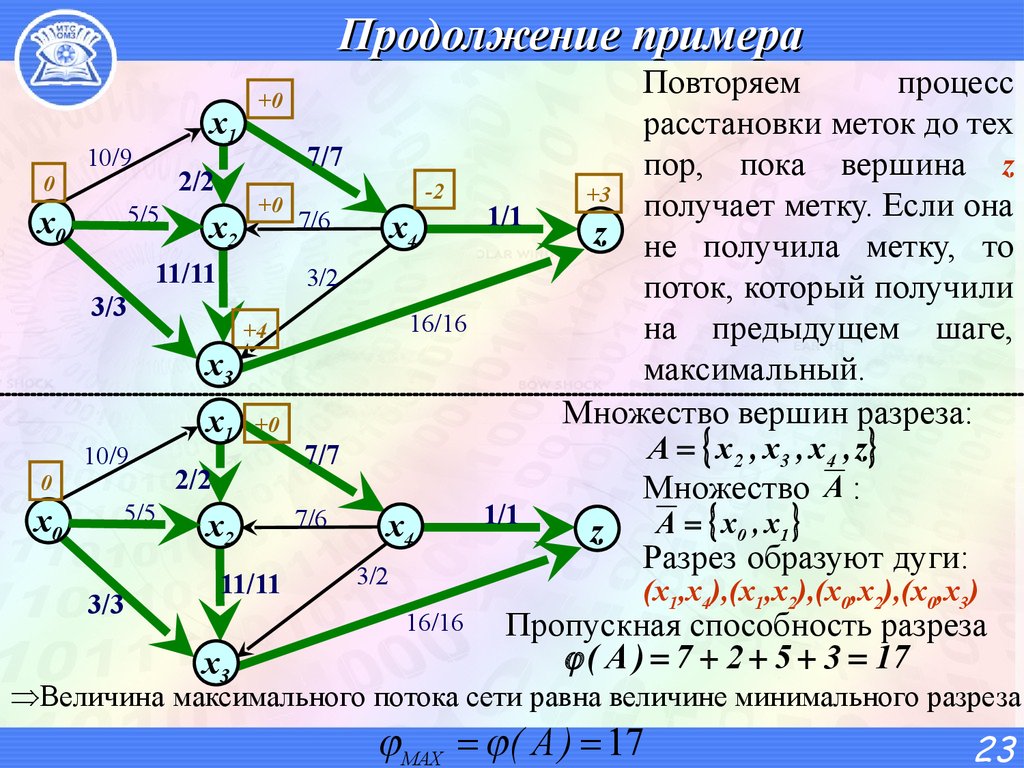
Повторяем
процесс
расстановки меток до тех
пор, пока вершина z
+3
получает метку. Если она
z не получила метку, то
поток, который получили
на предыдущем шаге,
максимальный.
Множество вершин разреза:
A x 2 , x 3 , x 4 , z
Множество A :
A x0 , x1
z
Разрез образуют дуги:
(x1,x4),(x1,x2),(x0,x2),(x0,x3)
Пропускная способность разреза
( A ) 7 2 5 3 17
Величина максимального потока сети равна величине минимального разреза
MAX ( A ) 17
23