概率论与数理统计

1.

惟真惟实
概率论与数理统计
教师 芮杰
15610552978
2019年QQ群 761127546

2.

惟真惟实
一、什么是概率

3.

二、生活中的概率问题
例1
北京奥运会圆满闭幕 某玩具厂商为推销其生产的
福娃玩具 特举办了一次有奖活动 设立了一个转盘
如图所示被等分成12个扇形区域。顾客随意向转盘内投
掷一点 如果落在转盘红色区域 顾客则可获得一套福
娃玩具。问顾客能得到一套福娃玩具的概率是多少

4.

• 例2
十一大促销 在淘宝上买的货物终于到
了 快递发短信给你 下午4点到5点将到
达您的送货地址 请注意接收。那您等候
时间不超过10分钟的概率是多少

5.

6.

生活中的概率问题
• 例3
在2014年世界杯半决赛第二场的比赛
中 阿根廷队和荷兰队在大战120分钟后
仍然战平 双方进入点球大战 荷兰队
在接下来的4次点球机会中 至少射入2
次的概率是多少

7.

例4
据统计青岛地区 30 岁单身人士在 5
年内结婚的概率为 0.98 仍然未婚的概
率为 0.02 保险公司欲开办单身险 参
加者需交纳 100 元 若 5 年内仍单身 则
赔偿 a 元 应该如何定 a 才能使公司可
期望获益
若有 10000 个人投保 公司期望总获益多
少

8.

例5
今年 20 岁明年 18 岁的概率是多
少
纯净水在标准大气压下 加热
到100摄氏度 沸腾的概率是多少

9.

必然现象与随机现象
必然现象 在一定条件下 某些事
情一定发生或一定不发生的现象。
Necessity Phenomenon
随机现象 在一定条件下 可能发
生也可能不发生的现象。
Random Phenomenon

10.

任务与研究方式
概率论与数理统计的任务:
The Task of Probability and Statistics
研究和揭示随机现象的统计规律性。
研究方式 Study manner
从数量的侧面研究随机现象统计规律。
Statistics Law

11.

绪
论
篇
• 概率论起源
• 发展简史
• 应用前景
• 学习方法指导

12.

概 率 论 起 源
Origin
概率论与数理统计是一门古老的学科
它起源于十七世纪资本主义上升的初期 这
时航海商业有了很大的发展 关闭的封建社
会经济正在被航海商业经济所取代。然而航
海商业是冒风险的事业 人们自然要关心大
量投资是否有利可图 怎样估计出现各种不
幸事故与自然灾害的可能性 在桥牌活动中
经常需要判断某种花色在对方手中的分配等
等。从某种意义上讲 概率论与数理统计正
是从研究这类问题开始的。

13.

发 展 简 史
Simple history
随机发生器——骰子的产生
公元前1500年 古埃及 “猎犬与胡狼”
公元前1400年 古埃及 骰子产生
骰子 对面之和为7
公元前1200年 用脚上的距骨来做骰子
概率思想的萌芽——文艺复兴时期
意大利
1477年 但丁《神曲》
在该书的“编印缘起”中讲到了投掷
三颗骰子可能出现的各种结果.

14.

代表人物
卡尔达诺 1501-1576 意大利数学和医学
教授
1526年 《机会性游戏手册》 1663年出版
伽利略 1613年和1623年之间 《关于骰子
游戏的思想》
他解释了在抛掷三颗骰子时为什么会有216
种同等可能的结果 以及为什么三颗骰子的
某些和数的出现看来似乎有同样大小的可能
性 而玩骰子的人们却认为不是同等可能。
比如和数为9和和数为10哪个更占优势

15.

概率的产生
点问题
对于数学中一个非常特别的问题的解法
的探求成为数学化的概率科学产生的标
志之一 这个问题被称作“点问题”。
点问题的起源故事
话说 1654年法国的一位军人德.梅勒
语言学家、古典学者

16.

德.梅勒和他的一个朋友每人出赌注30个金
币 两人各自选取骰子中的一个点数 谁先
掷出该点数次数多 谁就赢得全部赌注。德.
梅勒选的点数“5” 他的朋友选择的点数
“3”。
在游戏进行了一会儿后 德.梅勒选的
点数“5”出现了2次 而他的朋友选择的点
数“3”只出现了一次。这时候 德.梅勒由
于一个紧急事情必须离开 游戏不得不停止。
他们该如何分配赌桌上的60个金币的赌注呢

17.

帕斯卡
法国“最伟大的天才”
费马
业余数学家之王
两人在通信中正确解决了“点问题” 还创
造了一种研究的传统——用数学方法 主要
是组合数学 研究和思考机会性游戏。被称
为“数学史上的一个里程碑”。

18.

惠更斯 荷兰 1657年 《论掷骰子游戏
中的计算》——概率论中最早的论著
早期概率论的真正创立者是帕斯卡、费马
和惠更斯 这一时期被称为组合概率时期
概率的发展
瑞士数学家族——贝努利家族
雅可布.贝努利 提出“贝努利大数定律”
并花了20年的时间来证明。
1713年 出版《猜度术》。
尼古拉.贝努利 提出著名的“圣彼得堡问题”

19.

拉普拉斯 法国
明确给出概率的古典定义
证明了“棣莫佛—拉普拉斯中心极限定理”
建立了观测误差理论和最小二乘法
1812年 出版《分析的概率理论》
成为严谨的学科
1906年 俄数学家马尔科夫提出“马尔科夫链”
1934年 前苏联数学家辛钦(1894-1959)提出
“平稳过程理论”以及“辛钦大数定律”
20世纪初 完成了勒贝格测度与积分理论及
随后发展的抽象测度和积分理论

20.

1933年 柯尔莫哥洛夫 《概率论基
础》
首次给出概率的测度论式定义和一套严
密的公理化体系 其公理化方法成为现
代概率论的基础 使概率论成为严谨的
数学分支。
电子计算机的问世 进一步加速了概率论与
数理统计的发展。六十年代后 形成了许多
新的统计分支 时间序列分析、统计推断、
稳健统计、投影寻踪等。

21.

应 用 前 景 Prospect
概率论与数理统计应用呈现出极其壮观
的局面 尤其在质量管理、计量经济学、计
量心理学、金融数学方面起着重要的作用。
数理统计已渗透于工业统计、农业统计、水
文统计、统计医学、统计力学、统计物理学、
统计化学、统计教育学、统计体育学、统计
心理学等许多领域。气象预报、产量预报、
地震预报、石油勘探开发、可靠性工程等凡
是有数据需要处理的地方 都离不开概率统
计。因此概率论与数理统计作为一门应用数
学课程是非常重要的。

22.

学习方法指导
学习概率论与数理统计重点要理解掌握
它的基本概念、基本理论和常用统计方法的
具体应用。
理解实质 掌握内涵 循序渐进
抓住典型 触类旁通 开拓思路
善于分析 寻找规律 勇于创新
注意加强前后知识的联系 善于把新问
题化作老问题加以解决 掌握解决处理实际
问题的一般方法 逐步提高分析问题、解决
问题的能力。

23.

使用教材及参考书
教材 《随机数据处理方法》 第三
版 石大出版社 王清河等编著。
参考书 1.《概率论与数理统计》 第
三版 高教出版社 盛骤等编。
2. Introduction to Probability and Statistics,
Sixth Edition ,Mendenhall .
3.《概率论与数理统计学习指导》
胶印本 常兆光、王清河等编著

24.

概
率
论
篇
第一章 随机事件与概率
第二章 随机变量及其分布
第三章 随机变量的数字特征
第四章 大数定律与中心极限定理

25.

第一章 随机事件与概率
随机试验与随机事件
频率与概率
等可能概型、几何概型
条件概率
事件的独立性
• 综 合 练 习

26.

§1.1 随机试验与随机事件
Random Experiments and Random Events
随机试验
随机事件
样本空间
Sample Space
事件之间的关系及运算

27.

一.随机试验
Random Experiments
E1
掷一枚硬币 观察正、反面出现的情况。
E2
一射手射击 直到击中为止 观察射击情况
E3
从一批灯泡中任意抽取一只 测其寿命。
1 试验可以在相同条件下重复进行
2 每次试验的可能结果不止一个 但能
事先明确试验的所有可能结果
3 进行一次试验之前 不能确定哪一个
结果会出现。
具有以上三个特征的试验叫做随机试验。
简称为试验 用记号 E 表示。

28.

二.随机事件 Random Events
随机试验中的每一个可能结果称为随机事件
简称为事件 常用大写字母 A B C 等表示。
例
投掷一枚骰子 观察可能出现的点数
1. 事件A 出现的点数为奇数
2. 事件B 出现的点数小于4
3. 事件 e1 :出现1点
4. 事件 ei :出现的点数为i(i=2,3,4,5,6)
当事件 e1 , e3 或 e5 发生时 A发生 即
A { e1,e3,e5}.

29.

不可能再分的事件
基本事件
事件
分类
由基本事件复合而成的事件。
复合事件
必然事件: 一定发生的事件,记作 。
不可能事件:一定不发生的事件,记作 。
投掷一枚硬币的基本事件:
e1 :{H}
e2 :{T}
依次投掷两枚硬币的基本事件:
e1:{HH} e2 :{HT} e3 :{TH} e4 :{TT}
投掷一枚骰子的基本事件和复合事件
事件 ei 和事件A 出现的点数为奇数

30.

需要指出的是
无论是必然事件、随机事件还是不可
能事件 都是相对“一定条件”而言的。
条件发生变化 事件的性质也发生变化。
例如 抛掷两颗骰子 “出现的点数
之和为 3 点”及“出现的点数之和大于 3
点” 都是随机事件。若同时抛掷 4 颗骰子
“出现的点数之和为 3 点”
则是不可能事件了
而“出现的点数之和大于 3 点”则是必然事件了。
为了以后讨论问题方便 通常将必然事件和
不可能事件看成是特殊的随机事件。

31.

基本事件 记为e
复合事件 记为A、B等
随机事件
特殊事件 必然事件 记为
不可能事件 记为 。

32.

三.样本空间
Sample Space
样本空间:
由试验所有可能结果构成的集合称为样
本空间 通常用符号 表示 中的每个元
素称为样本点。
基本事件:
只包含一个样本点的事件称为基本事件

33.

Exp1-1 将一枚硬币连掷两次 写出这一随
机试验的样本空间。
SOL 记正面为 H ,反面为 T , 为样本空间 则
={ HH HT TH TT }
ˆ {e1 e2 e3 e4 }
Exp1-2 记录某电话交换台在一分钟内收到
的呼叫次数 写出样本空间 。
SOL ={0 1 2 3, }

34.

Exp1-3 在一批灯泡中任取一只测其寿命 样
本空间为 = t | t 0, t R 而寿命小于 5 小
时为一随机事件 为 A = t | 0 t 5, t R 。
样本空间中的样本点是由试
需要指出的是
Aim
验目的所决定的。
1 将一骰子连续抛掷 3 次 观察出现的
4
18 }
点数之和 ={ 3
2 将一骰子连续抛掷 3 次 观察六点出
1
2
3 }。
现的次数 ={ 0
以上两例 同是抛掷一颗骰子 3 次 由于试
验目的不同 其样本空间也就不一样。

35.

作业
以小组为单位 在相同
的条件下扔一枚均匀的
硬币100次 统计正面、反面
出现的次数。

36.

四. 事件及其运算关系
若记 样本空间 不可能事件 e 基本
事件 A B A1 A2
An 为随机事件。则有事
件之间的运算关系如下
1 包含关系 记作 A B 即事件 A 则事件 B 一定发生
2 相等关系 记作 A B 即 A B 且 B A。
3 和事件 记作 A B 即 A, B 至少有一个发生。
4 积事件 记作 A B (简记为 AB
即 A 发生且 B 发生。
5 差事件 记作 A B A B AB
表示事件 A发生而事件 B 不发生
。

37.

推广
有限个事件和事件记作
n
A1 A2 An ˆ Ai
i 1
无限个事件和事件记作
A1 A2 An ˆ Ai
i 1
有限个事件的积事件记作
n
A1 A2 An ˆ Ai
无限多个事件的积事件记作
i 1
A1 A2 An ˆ Ai
i 1

38.

6 互不相容 互斥
若 AB 则称事件 A 与事件 B 互不相容
2
)
推广 若 i j Ai Aj (i、j 1
An 为两两互不相容的。
则称 A1 A2
7 对立事件 逆事件
若 AB 且 A B 则称事件 A 与事件 B 互逆
即 A = B B = A。

39.

8 摩根定理 对偶原理
A B A B
A B A B
9 运算规律(交换律 结合律 分配律)
交换律 A B B A,
A B B A,
结合律 A ( B C ) ( A B) C ,
A ( B C ) ( A B) C
分配律 A ( B C ) ( A B) ( A C ),
A ( B C ) ( A B) ( A C ),

40.

Exp1-5 将一枚硬币连掷两次
记 A1 表示 “第一次出现正面” 即
A1 {HH HT } ˆ e1 e2
A2 表示 “两次出现同一面” 即
A2 {HH TT }
ˆ e1 e4
A3 表示 “只出现一次正面” 即
A3 {HT TH }
ˆ e2 e3
则 A1 A2 {HH HT TT }
A1 A2 {HT }
A1 A2 {HH } e1 ,
由于 A2 A3 故 A2 与 A3 互不相容
又由于 A2 A3 所以 A2 与 A3 互逆。
结论 两事件互逆必互不相容 反之不然。

41.

需 要 指 出 的 是 熟 练 掌 握 事 件 间 的 运 算 关
系是正确计算随机事件的概率之基础。在研究
实际问题时 往往需要考虑试验结果中各种可
能的事件 而这些事件通常是相互关联的。研
究事件之间的关系 进而研究这些事件的概率
之间的关系 就能够利用简单事件的概率去推
算较复杂事件的概率。因此应当善于把某些复
杂事件表示为若干个简单事件的和或积。要实
现这一点 除正确理解事件间关系及运算外
还必须对具体问题进行具体分析。
CH1

42.

例1-6 设A,B,C 为三个事件 试用事件之间的运
算关系表示下列事件
1 A发生而B与C都不发生
A B C ABC
A B C
2 A,B,C恰有一个发生
( ABC ) ( ABC ) ( ABC )
3 A,B,C至少有一个发生
A B C
4 A,B,C至多有两个发生。
A B C
A B C
思考 A,B,C 都不发生与A,B,C 不都发生的区别

43.

§1.2
频率与概率
Frequency and Probability
一.频
率
二.概率的统计性定义
三.概率的公理化定义
CH1

44.

一.频
率
在概率论中 将描述随机事件 A 发生的可能性大小
的数记为 P( A) 称 P( A) 为随机事件 A 的概率。
[引例] 将一硬币连续掷
n 次 事件 A {H } ,
n( A) 表示 n 次试验中 A 出现的次数 则
n
(
A
)
f n ( A) ̂
n
在一定程度上能反映事件 A 发生的可能性大小。

45.

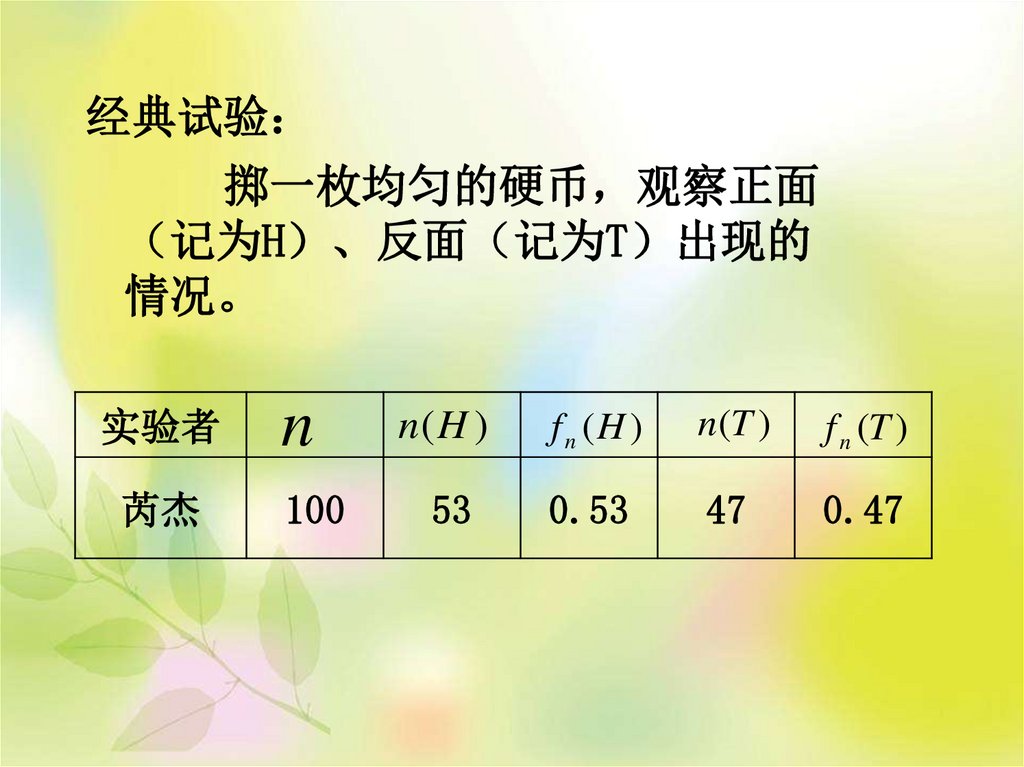
经典试验
掷一枚均匀的硬币 观察正面
记为H 、反面 记为T 出现的
情况。
实验者
芮杰
n
100
n(H )
f n (H )
n (T )
f n (T )
53
0.53
47
0.47

46.

表 1-1
n =5
实验序号 n( A) f n ( A)
1
2
0.4
2
3
0.6
3
1
0.2
4
5
1.0
5
1
0.2
6
2
0.4
7
4
0.8
8
2
0.4
9
3
0.6
10
3
0.6
n =50
n( A) f n ( A)
22 0.44
25 0.50
21 0.42
25 0.50
24 0.48
21 0.42
18 0.36
24 0.48
27 0.54
31 0.62
n =500
n( A) f n ( A)
251 0.502
249 0.498
256 0.512
253 0.506
251 0.502
246 0.492
244 0.488
258 0.516
262 0.524
247 0.494

47.

表 1-2
实 验 者
n
n( A)
f n ( A)
4040
2048
0.5070
K.皮尔逊 12000
6019
0.5015
K.皮尔逊 24000
12012
0.5005
蒲
丰
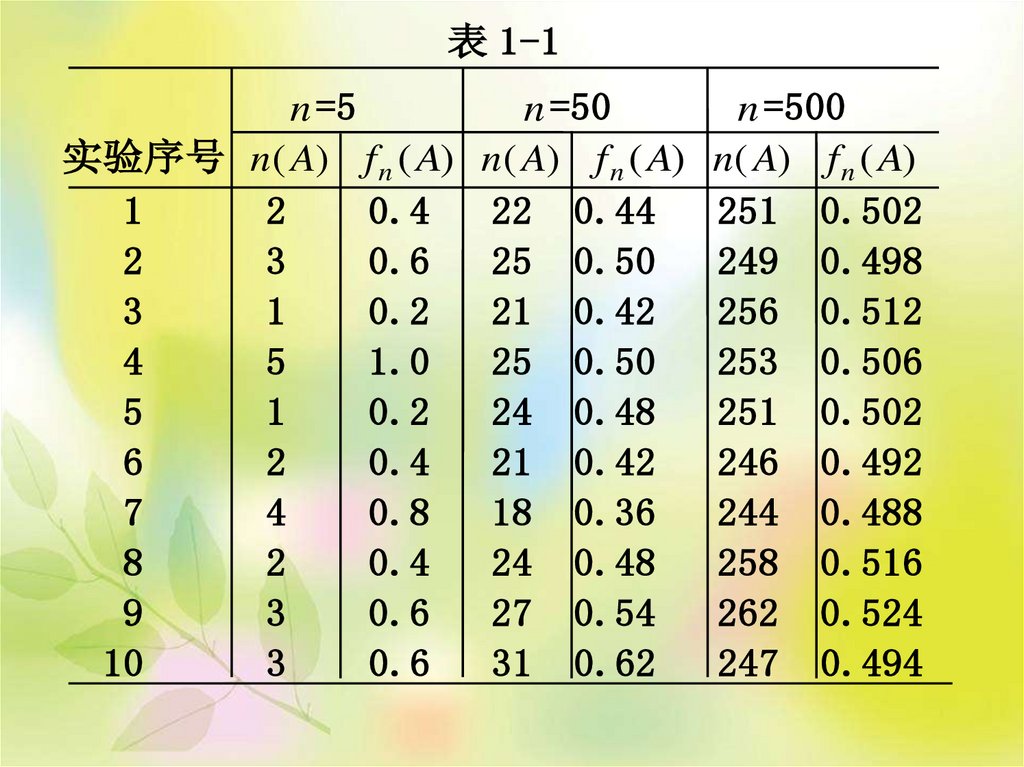
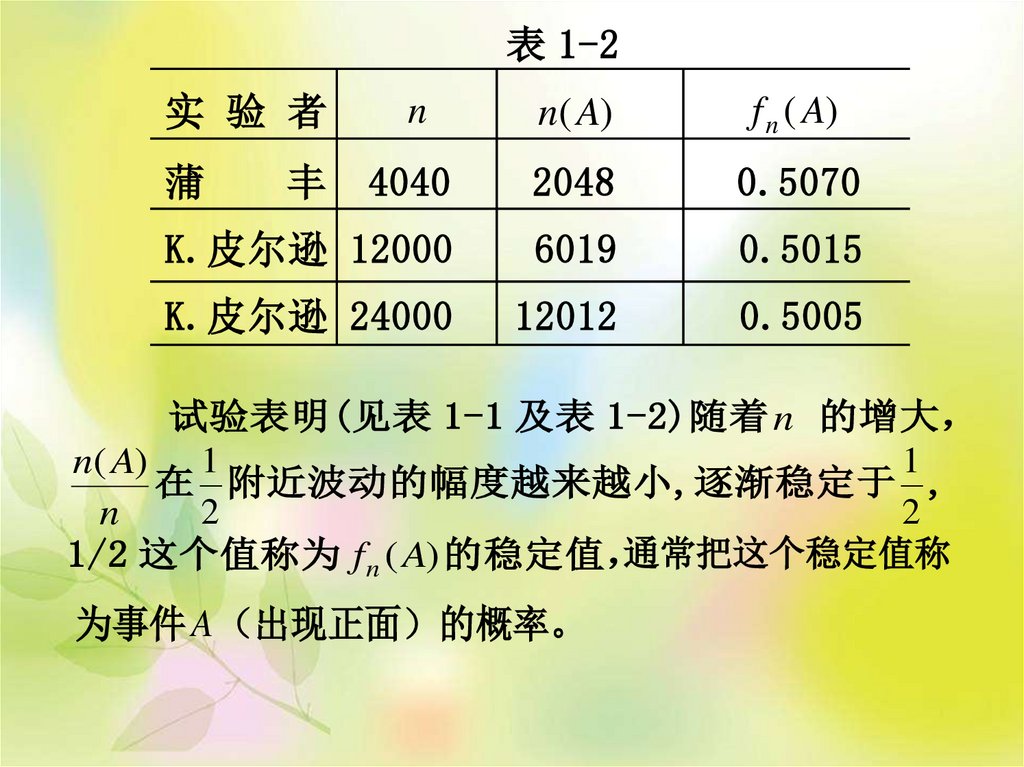
试验表明(见表 1-1 及表 1-2)随着 n 的增大
1
n( A) 1
在 附近波动的幅度越来越小,逐渐稳定于 ,
2
2
n
通常把这个稳定值称
1/2 这个值称为 f n ( A) 的稳定值
为事件 A 出现正面 的概率。

48.

频率定义
Definition of Frequency
定义 1-1 设 E 为随机试验 A 为其中任一事件
n( A) 为事件 A 在 n 次重复试验中出现的次数 则称比
n( A)
为 n 次试验中 A 出现的频率 记为
值
n
n( A)
1-1
f n ( A) ˆ
n
其中 n( A) 称为事件 A 在 n 次重复试验中出现的频数。
当 n 增大时 f n ( A) 逐渐稳定于某一个确定值 p 上
称 p 为频率的稳定值。
由频率的定义不难看出 f n ( A) 具有以下性质

49.

频率 f n ( A) 具有以下性质
Property
1 非负性 0 f n ( A) 1
2 规范性 f n ( ) 1
3 可加性 若事件 A 与事件 B 互不相容 则
f n ( A B) f n ( A) f n ( B)
Am 两两互不相容 则
进一步 若 A1 A2
m
m
i 1
i 1
f n ( Ai ) f n ( Ai )

50.

二.概率的统计性定义
Statistical definition of Probability
需
要
指
出
的
是
频率在一定程度上反映了事件 A 发生的
可能性大小 但在一定条件下做重复试验
其结果可能是不一样的 因此不能用频率代
替概率。不过由贝努力大数定律保证 频率总
能稳定在某个固定数 p 周围 并且
n
f n ( A)
p
由此得概率的统计性定义如下
定义 1-2 在不变条件下做大量重复试验 称在重复试
验中事件 A发生的频率的稳定值 p 为事件 A 的概率 记
为 P( A) 。

51.

三.概率的公理化定义
Axiomatize Definition
定义 1-3 设 E 为随机试验 为它的样本空间
对 E 中的每一个事件 A 都赋予一个实数 记为 P( A)
且满足
1 非负性 0 P( A) 1
2 规范性 P( ) 1
3 可加性 若 A1 , A2 , , An , 两两互不相容
i 1
i 1
则有 P( Ai ) P( Ai ) 。
则称 P( A) 为事件 A 的概率。

52.

概率 P( A) 的性质如下
P ( ) 0
2 若 A1 , A2 , , An 两两互不相容 则
1
n
n
i 1
i 1
P ( Ai ) P( Ai )
3 若 A 的对立事件记为 A 则 P( A) 1 P( A )
Proof
由于 A A 且 A A 故由性质 2
及规范性得
1 P( ) P( A A ) P( A) P( A )
即 P( A) 1 P( A ) 。

53.

4 若 A B 则 P( B A) P( B) P( A) 且
P( A) P( B)
Proof 由于 B A ( B A) 而A ( B A)
所以由性质 2 得
P( B ) P( A ( B A)) P( A) P( B A)
即 P( B A) P( B) P( A) 。
又 P( B A) 0 故 P( B) P( A) 0 即 P( A) P( B) 。
推广 任意的两个事件 A,B 则有
P( B A) P( B) P( AB)

54.

5 P( A B ) P( A) P( B ) P( AB )
Proof 由于A B A ( B AB ) 而A ( B AB )
所以由性质 2 、 4 得
P( A B ) P( A) P( B AB ) P( A) P( B ) P( AB )
此性质可推广到任意有限个事件 A1 , A2 , , An 即
P ( A1 A2 A3 ) P ( A1 ) P ( A2 ) P ( A3 )
P ( A1 A2 ) P ( A1 A3 ) P ( A2 A3 ) P ( A1 A2 A3 )
n
n
n
n
i 1
i 1
i j
i j k
P( Ai ) P( Ai ) P( Ai A j ) P( Ai A j Ak )
加法公式
( 1) n 1 P( A1 An )

55.

Exp1-7 已知事件 A 、 B 满足 P( AB ) P( A B )
且 P( A) p 求 P(B ) 。
SOL one 由于
P( AB ) P( A B ) = P( A B ) 1 P( A B )
=1 P( A) P( B) P( AB )
从而得1 P( A) P( B) 0 即
P( B) 1 P( A) 1 p
SOL two 由性质 5 知
P(B) = P( A B) P( A) P( AB )
性质 5
=1 P( A B ) P( A) P( AB )
性质 3
=1 P ( A B ) P ( A) P ( AB ) 对偶原理
=1 P( A) =1 p
已知条件

56.

Exp1-8 对 于 事 件 A 、 B、C 有 P( AC ) 1 / 8
P( A) P( B) P(C ) 1 / 4 P( AB ) P( BC ) 0 求 A 、
B、C 至少出现一个的概率。
解 由概率的加法公式
P( A B C ) P( A) P( B ) P(C )
P( AB ) P( AC ) P( BC ) P( ABC )
而 ABC AB 所以 P ( ABC ) P ( AB ) 0 故
P( ABC ) 0 即
1
1 5
P( A B C ) 3
4
8 8

57.

Exp 1-9 设 A B 为随机事件 P( A) 0.7
P( A B) 0.3 ,
解 由
求 P( A B ) .
P( A B) P( A) P( AB)
以及题设条件 得
P( AB) 0.4
从而由对偶原理以及概率的性质3可知
P( A
B ) P( A B) 1 P( AB) 0.6
类似问题 设 A B 为随机事件 P( A) 0.6
P( B A) 0.2 求 P( A
B) 。