Similar presentations:
Теория вероятностей и математическая статистика
1.
Теория вероятностей иматематическая статистика
Имя: Сяо е Лян
邮件地址: xiaoyeliang@neusoft.edu.cn
办 公 室: 基础教学部 A1-102-a
电 话: 84835093
学生门户网: http://stu.neusoft.edu.cn
在线课程 http://neusoft.benke.chaoxing.com
2020年9月11日
2.
Краткое содержаниеЧто это
такое?
Зачем
учиться?
Чему
научит
ься?
Как
учитьс
я
Как
провери
ть?
2020年9月11日
3.
Во-первых, что это такое-основыкурса
Характер курса: обязательный
Расписание занятий: всего 36 академических
часов Неделя академических часов: 2
академических часа
Формы обучения: лекция в классе, занятия в
классе, онлайн-обучение,послешкольные задания
Основы курса: Основы вероятности в вузе,
производные в высшей математике, знание
интегралов
2020年9月11日
4.
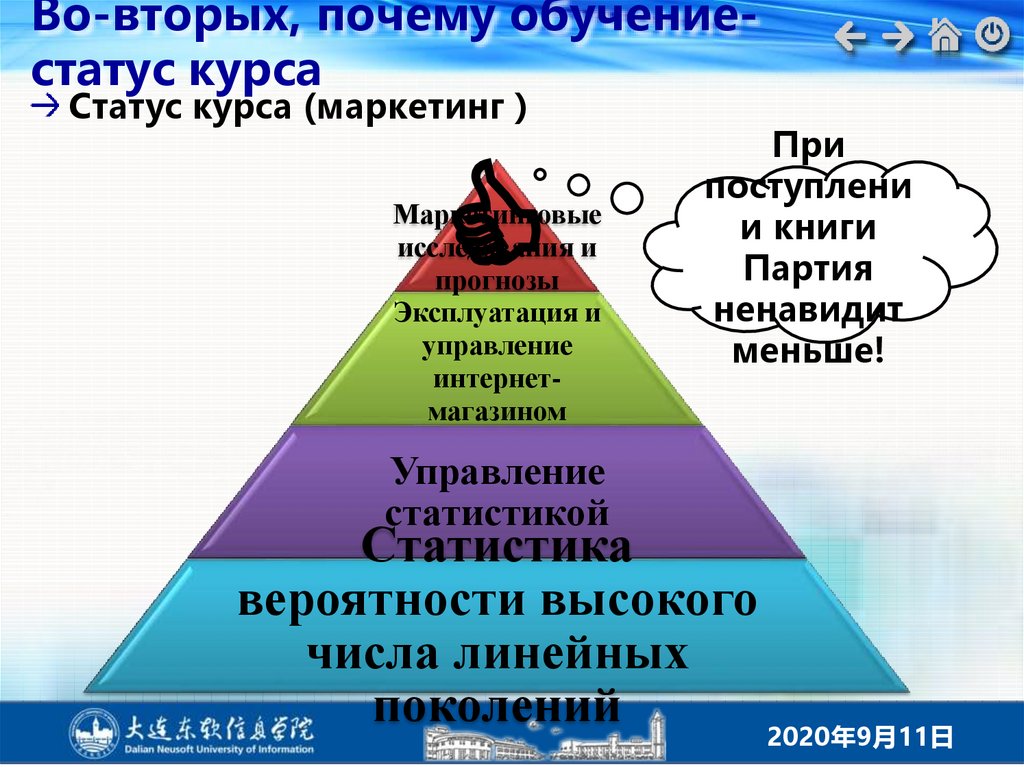
Во-вторых, почему обучениестатус курсаСтатус курса (маркетинг
C
Маркетинговые
исследования и
прогнозы
Эксплуатация и
управление
интернетмагазином
Управление
статистикой
При
поступлени
и книги
Партия
ненавидит
меньше!
Статистика
вероятности высокого
числа линейных
поколений
2020年9月11日
5.
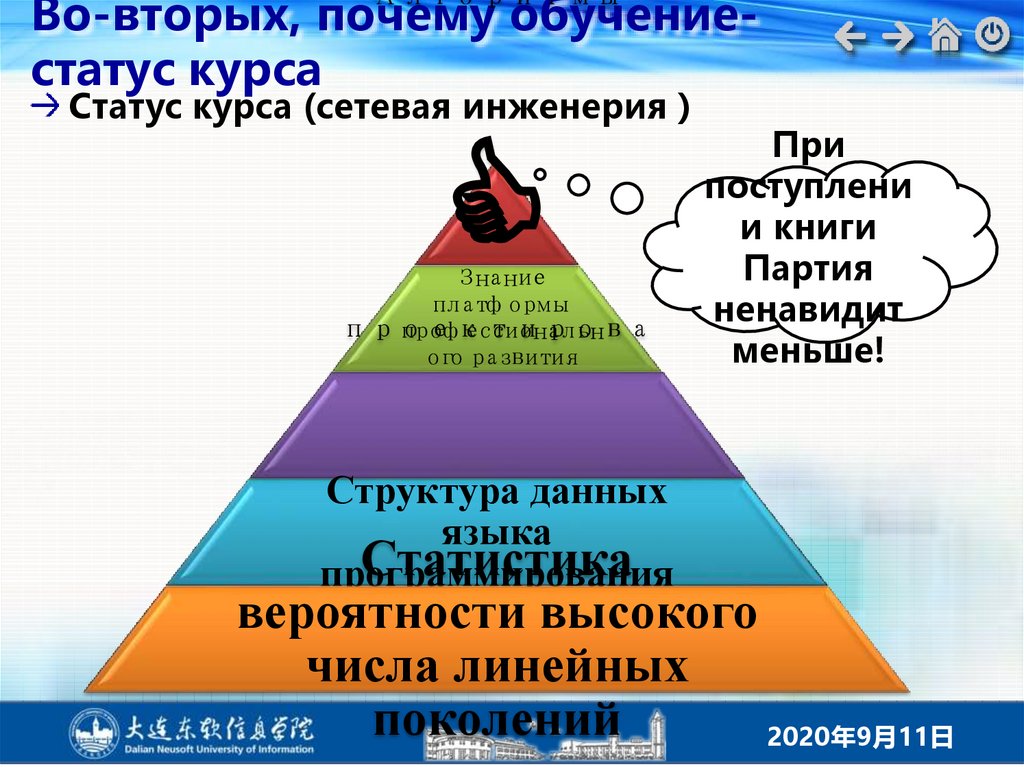
Во-вторых, почему обучениестатус курсаАлгоритмы
Статус курса (сетевая инженерия
C
Знание
плат
формы
проектирова
профессиональн
ог
ораз
вит
ия
Структура данных
языка
Статистика
программирования
При
поступлени
и книги
Партия
ненавидит
меньше!
вероятности высокого
ния
числа линейных
поколений
2020年9月11日
6.
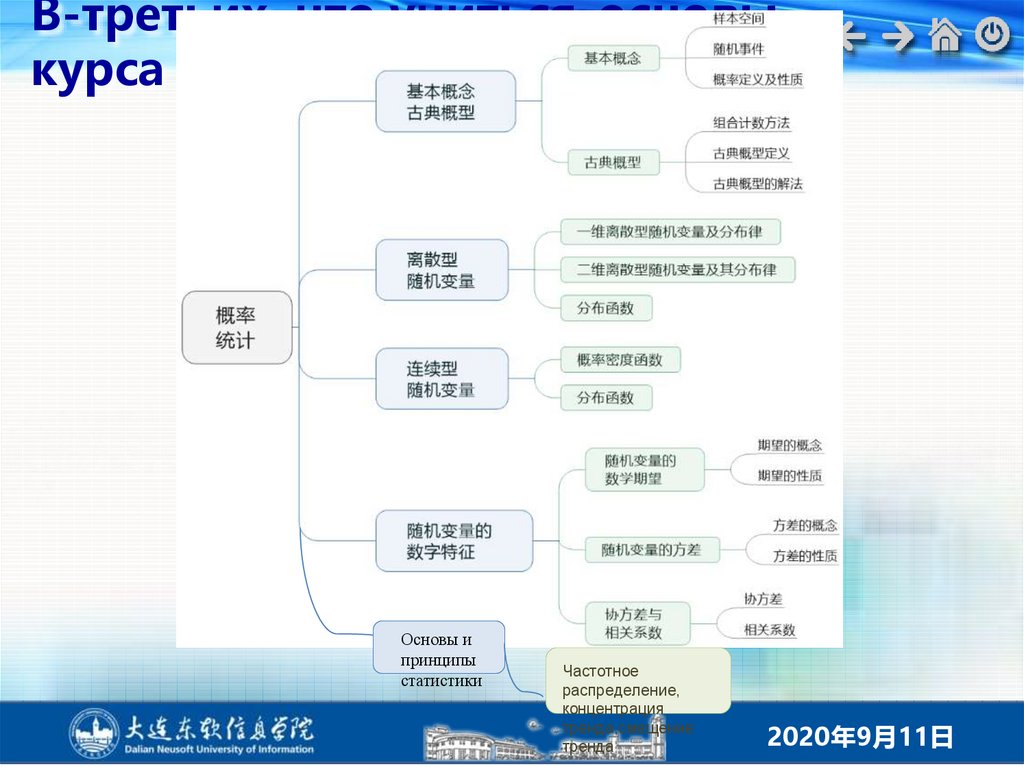
В-третьих, что учитьсясодержание курсачасть • Случайные события и
вероятности
перва
я
Глава • Случайные величины и их
распределение
втора
я
Глава • Числовые характеристики
случайных величин
треть
я
Глава • Основы и принципы
статистики
четве
ртая
Основные идеи, Основные понятия, основные
принципы, основные методы и практическое
применение
2020年9月11日
7.
В-третьих, что узнать-нескольковопросов
Почему жребий справедлив? Можете ли вы
объяснить это ясно?
На столе случайным образом помещается 10
продуктов, из которых есть 3 вторичных
продукта, взятых из любого из них дважды,
каждый раз, когда вы берете один, какова
вероятность того, что первый раз выкачаете
неполноценный продукт? Какова вероятность
того, что второй раз выкачаете неполноценный
товар?
2020年9月11日
8.
В-третьих, что узнатьпроисхождение теориивероятностей
Теория вероятности возникла из проблемы
азартных игр. Еще в середине 17-го века, когда во
Франции появились исследования по вопросам
азартных игр, любящий азартные игры Де мерес
задал своему приятелю Паскалю такие
вероятностные вопросы, как”распределение
ставок на ранний конец азартных игр для двух
человек".
В 1654 году математики Паскаль (1623-1662) и
Фермат (1601-1665) использовали комбинаторные
методы в переписке,чтобы дать решение о
распределении ставок.
1657, голландский математик Гюйгенс (C.Гюйгенс,
1629-1695) опубликовал "расчеты в азартных
играх", самую раннюю статью по теории
2020年9月11日
9.
Марков2020年9月11日
10.
Колмогоров2020年9月11日
11.
В-третьих, что узнатьпроисхождение теориивероятностей
1. Вопросы распределения ставок (1654 Паскаль и
ферма)
Если выигрыш в одной азартной игре был первым 6 раз,
а два игрока, выигравших 5 раз, выиграли 2 раза,
азартные игры были прерваны по какой-либо причине,
то распределение общей ставки должно быть разумным.
Есть две идеи
(1)a хочет выиграть, просто выиграйте еще одну игру. Это
может быть в следующих подач 1, 2, 3, 4 и вероятность
соответственно 1/2, 1/4, 1/8, 1/16
Вероятность выигрыша равна 1/2+1/4+1/8+1/16=15/16
B вероятность победы 1-15 / 16=1/16
(2)B, чтобы выиграть, вы должны выиграть 4 игры подряд,
вероятность каждой победы равна 1/2,
Вероятность победы в 1/16
Вероятность выигрыша 1-1 / 16=15/16
2020年9月11日
12.
Занятия в классеПризовой фонд устанавливается в размере 1 000
долларов США за один турнир по настольному
теннису.В турнире указывается, кто победит в трех
сетах и кто получит все призовые деньги.После
того,как он сыграл три сета, две победы и одно
поражение, игра должна быть прервана по какойто конкретной причине.Вопрос: как эти 1000
долларов должны быть распределены, чтобы
быть справедливыми?
2 победы и 1 поражение, по 2: 1?
Правильный метод очков, чтобы продолжать
лежать, чтобы увидеть, как шансы на победу в
конце а, б, не более двух сетов, чтобы разделить
выигрыш
这2盘有3种可能结果: 甲、乙甲、乙乙.
2020年9月11日
13.
В-третьих, что узнать-вопросДжека
Джек и Тони часто делают ставки на кости:
бросают две кости и предсказывают сумму очков
на обеих костях. Джек всегда угадывает 5 очков,
Тони всегда угадывает 8 очков, Джек всегда
проигрывает. Итак, Джек подумал: "Разве ему не
повезло?"
Экспериментируйте со всеми возможными
результатами
1+1 1+2 1+3 1+4 1+5 1+6
2+1 2+2 2+3 2+4 2+5 2+6
3+1 3+2 3+3 3+4 3+5 3+6
4+1 4+2 4+3 4+4 4+5 4+6
5+1 5+2 5+3 5+4 5+5 5+6
6+1 6+2 6+3 6+4 6+5 6+6
2020年9月11日
14.
В-третьих, что узнать-Вопрос днярождения
“在一个有64人的班级里 至少有两人生日相同”的概率为多少
2020年9月11日
15.
Что мы учим?——Объектисследования по теории
вероятностей
В мире, в котором мы живем,,Полная неопределенности, от
простых игр с возможностями, таких как забрасывание
монетами, забрасывание костями и игра в покер, до
сложных социальных явлений, от рождения младенцев до
воспроизводства всего мира, от падения метеорита до
тысячи изменений природы.……Мы постоянно
сталкиваемся с неопределенностью и случайностью.,Это
все.Случайные явления.
2020年9月11日
16.
Что мы учим?——Объектисследования по теории
вероятностей
Количественное определение степени неопределенности случайных
явленийчтобы попытаться ответить на эти вопросы,20Начало века.. Нельзя
сказать, что эти усилия оказались весьма успешными, но те результаты,
которые уже получены, привели к революции во всех сферах
человеческой деятельности..
Эта революция открывает путь для изучения новых идей, развития
естественнонаучных знаний, процветания человеческой жизни.. Кроме
того, мы изменили наше мышление, чтобы мы могли смело изучать
загадки природы..
2020年9月11日
17.
Что мы учим?——Объектисследования по теории
вероятностей
Давайте начнем ".Количественное определение
неопределенности"Обучение на курсах, вот и все.
Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика
- математическая дисциплина, изучающая
случайные явления и их регулярность с помощью
математических методов..
2020年9月11日
18.
В-третьих, что учиться-основыкурса
Основы и
принципы
статистики
Частотное
распределение,
концентрация
тренда,смещение
тренда
2020年9月11日
19.
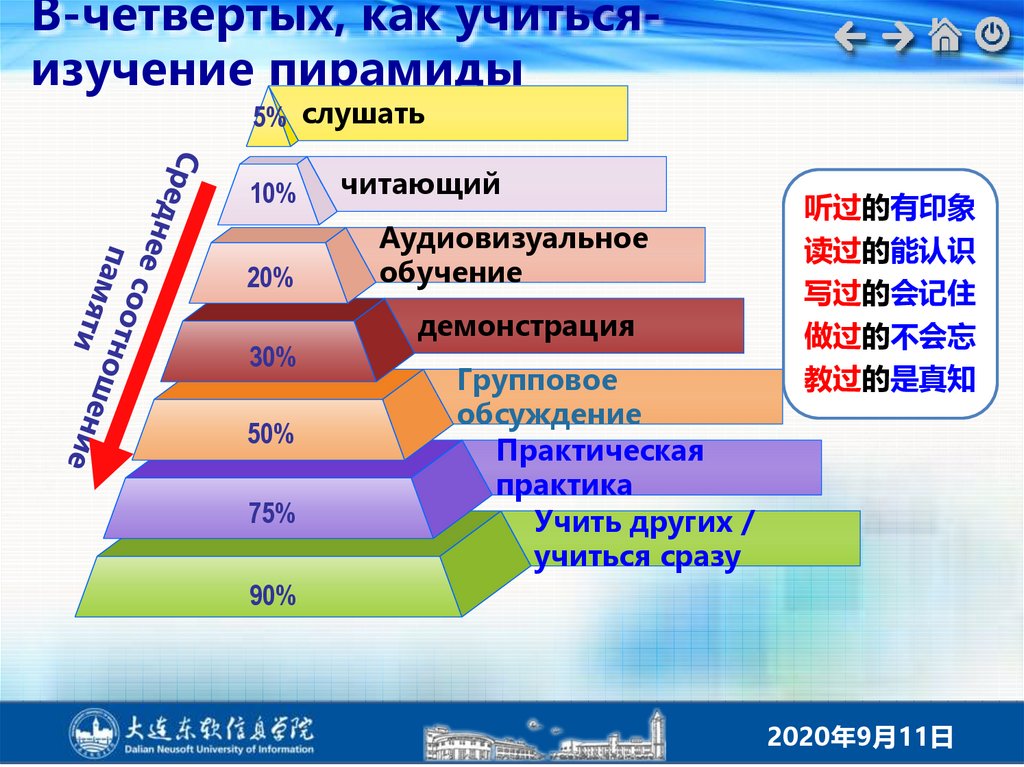
В-четвертых, как учитьсяизучение пирамиды5% слушать
10%
20%
30%
50%
75%
читающий
Аудиовизуальное
обучение
демонстрация
Групповое
обсуждение
Практическая
практика
Учить других /
учиться сразу
听过的有印象
读过的能认识
写过的会记住
做过的不会忘
教过的是真知
90%
2020年9月11日
20.
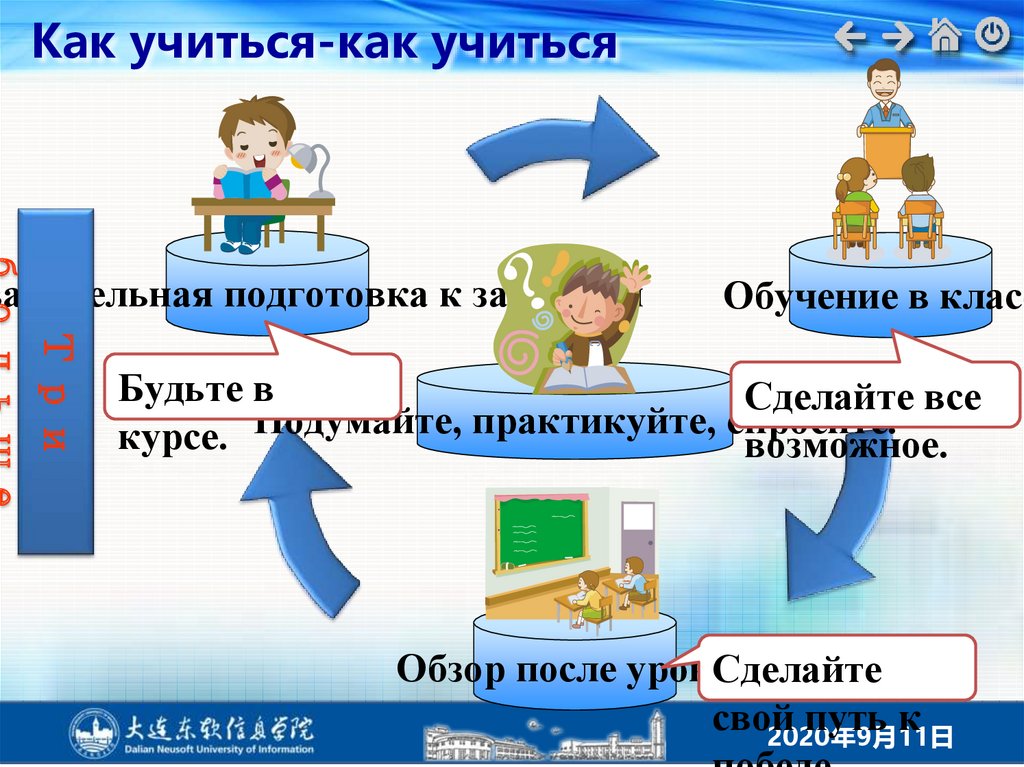
Как учиться-как учитьсяварительная подготовка к занятиям
Обучение в класс
Три
Будьте в
Сделайте все
курсе. Подумайте, практикуйте, спросите.
возможное.
Обзор после уроков
Сделайте
свой
путь к
2020年9月11日
21.
Как учиться-как учитьсяШесть
привычек
Привычки
самообуче
ния
Делайт
е
заметк
и в
классе.
Заве
ршен
ие
зада
ния
Позитив
ное
мышлени
Исполь
зовани
е
Использо
вание
2020年9月11日
22.
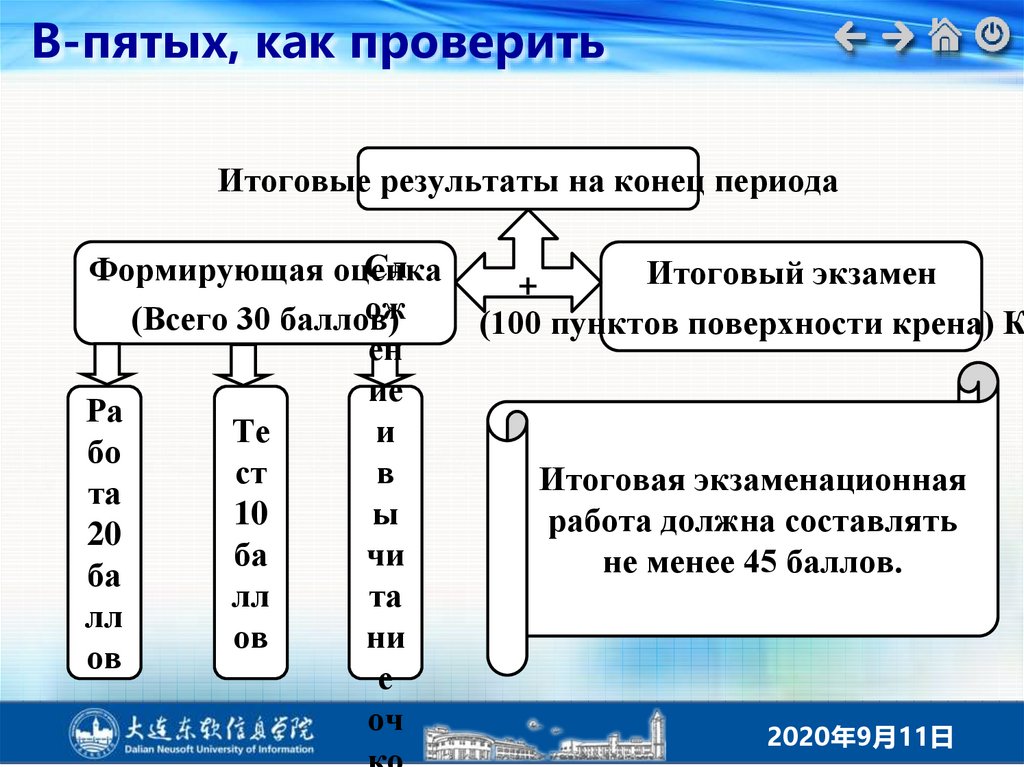
В-пятых, как проверитьИтоговые результаты на конец периода
Сл
Формирующая оценка
ож
(Всего 30 баллов)
ен
ие
Ра
Те
и
бо
ст
в
та
10
ы
20
ба
чи
ба
лл
та
лл
ов
ни
ов
е
оч
Итоговый экзамен
+
(100 пунктов поверхности крена) К
Итоговая экзаменационная
работа должна составлять
не менее 45 баллов.
2020年9月11日
23.
В-пятых, как формируютсяэкзаменационно-формальные
оценки
(1)посещаемость
累计缺课达到或超过总学时1/3 取消平时成绩和期末考试资格
Система удержания, верхний предел удержания не более
20 баллов.
(2)Добавление и вычитание очков в классе
К доске, чтобы сделать вопрос, правильно ответить на
вопрос, добавить 1 ~ 2 балла / раз, неправильно-1
балл/раз; в классе без разрешения учителя использовать
ноутбук, играть на мобильном телефоне-1 балл / раз.
(3)Работа (10 баллов)
Выполняйте задания по учебному пособию вовремя,
набирайте очки несколько раз и набирайте 10 баллов.
2020年9月11日
24.
В-пятых, как формируютсяэкзаменационно-формальные
оценки
(5)викторина (10 баллов
2020年9月11日
25.
Учебные материалыТеория вероятностей и математическая
статистика, Чжэцзянский университет шэншуй,
издательство высшего образования.
Учебник по основам теории вероятностей
(первый курс по вероятности), Шелдон М. Росс,
Тонг-Вэй, перевод Лян баошенг, издательство
2020年9月11日
26.
Учебные материалыКитайский университет MOOC
(http://www.icourses.cn/imooc)
2020年9月11日


















 mathematics
mathematics








