Similar presentations:
Силы сопротивления, действующие на рабочие органы сельскохозяйственных машин, при обработке почвы
1. тема: Силы сопротивления, действующие на рабочие органы, при обработке почвы.
1. Силы, действующие накорпус плуга.
2.
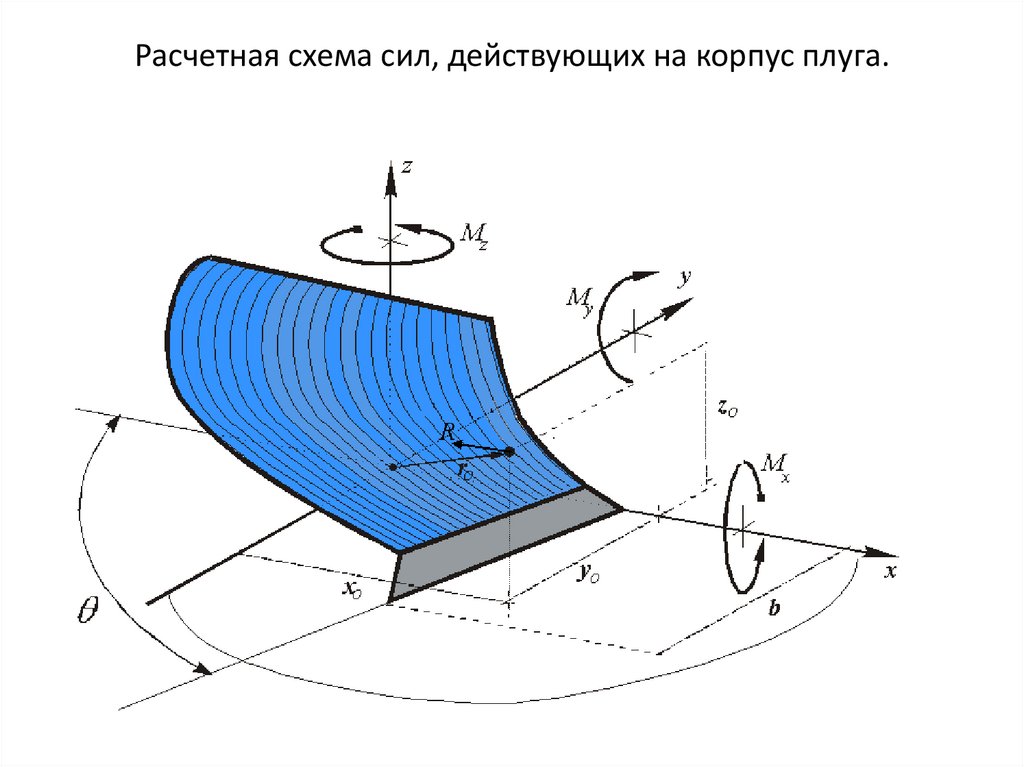
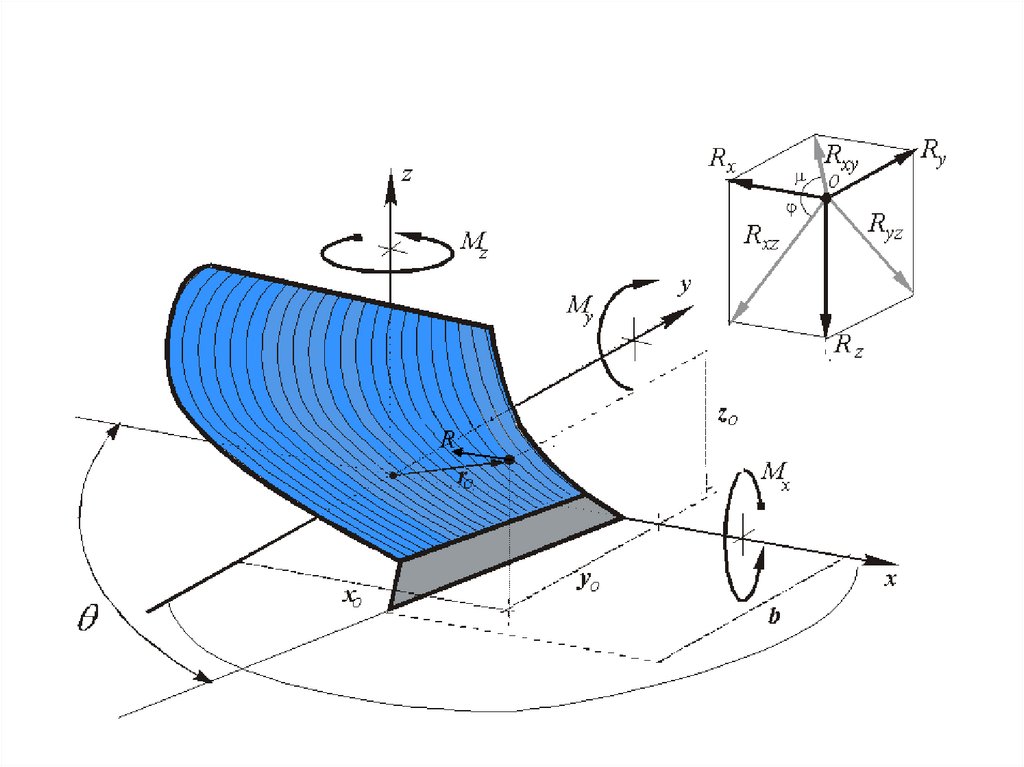
Расчетная схема сил, действующих на корпус плуга.3.
В общем случае систему элементарных сил, действующих на корпусплуга, можно привести к главному вектору- силе R, и главному моменту M
Главный вектор R, задается в виде проекций сил Rx; Ry; Rz на оси X, Y, Z
декартовой системы координат.
2
2
2
Значение вектора R, определяется по выражению: R Rx Ry Rz
Модуль вектора главного момента М можно записать в виде геометрической
суммы величин проекций главного момента на координатные оси:
M Мx 2 Мy 2 Мz 2
4.
5.
,На основе опытных данных установлено, что точка приложения
равнодействующей R
, имеет координаты:
xo=0,4·b cos ;
yo=0,4·b;
zo=(0,3..0,5)·а.
Горизонтальная составляющая сил Rx, кН действующая вдоль оси Х,
определяется по зависимости:
Rx=k·а·b,
где k - удельное сопротивление почвы, кН/м2;
а - глубина обработки почвы, м;
b - ширина захвата корпуса, м.
Значение сил Ry и Rz зависит от состояния лемехов, глубины обработки,
скорости движения, свойств почвы, типа и параметров рабочих органов и
определяются по выражениям:
R y c Rx
R z d Rx
где c и d – экспериментальные коэффициенты пропорциональности,
с =1/3,
d = 0,2
6.
При известных коэффициентахc
и
d
для определения положения главного
вектора R в пространстве достаточно знать величину проекции силы
Тогда косинусы углов примут следующий вид:
cos R; x
Rx
R
cos R; y
Ry
R
Rx
Rx 2 c 2 Rx 2 d 2 Rx 2
cRx
Rx 2 c 2 Rx 2 d 2 Rx 2
Rx.
1
1 c2 d 2
c
1 с2 d 2
Rz
dRx
d
cos R; z
R
Rx 2 c 2 Rx 2 d 2 Rx 2
1 c2 d 2
R
R R R
2
x
2
y
2
z
По значениям этих косинусов можно определить углы между направлением
действия силы R и осями координат.
7.
.При проведении прочностных расчетов стоек рабочих органов, важно знать,
как направлена проекция главной силы
, R на плоскость xy. Определим угол
между координатной осью x и вектором Rxy – проекцией главного вектора R
на плоскость xy. Для этого воспользуемся зависимостью
cos cos Rxy ; x
Модуль силы : Rxy
Следовательно,
Rx 2 Ry 2
cos cos Rxy ; x
Rx
Rxy
Rx 2 c 2 Rx 2 Rx 1 c 2
Rx
Rx
2
Rxy
Rx 1 c
1
1 c2
Аналогично можно получить значение угла между осью x и проекцией Rxz
главного вектора на плоскость xz:
cos cos( Rxz ; x)
Rx
Rx
1
Rxz Rx 1 d 2
1 d 2
8.
Кроме силы сопротивления R, на корпус плуга действует момент M,представленный в виде проекций Mx,My,Mz на координатные оси.
Модуль вектора главного момента М можно записать в виде геометрической
суммы величин проекций главного момента на координатные оси:
M Мx 2 Мy 2 Мz 2
.
Проекции моментов Mx, My, Mz определяются по зависимостям
yo
M x
Ry
x
M y o
Rx
zo
y R z R
Rz o z o y
zo
x o R z zo R x
R z
xo yo
xo Ry yo Rx
M z
R
R
x y
9.
Подставив в полученные выражения координаты (xo; yo; zo) точкиприложения главного вектора R и значения Rx , Ry и Rz рассчитаем
величины составляющих Mx, My, Mz главного момента М.
yo z o
0 ,4 b d Rx ( 0 ,3 0 ,5 ) a c Rx Rx [ 0 ,4 b d ( 0 ,3 0 ,5 ) a c ]
M x
Ry Rz
xo
M y
Rx
xo
M z
Rx
zo
0,4 b cos d Rx (0,3 0,5) a Rx Rx [0,4 b d cos (0,3 0,5) a]
Rz
yo
0 ,4 b cos c Rx 0 ,4 b Rx Rx ( 0 ,4 b c cos 0 ,4 b )
Ry
10.
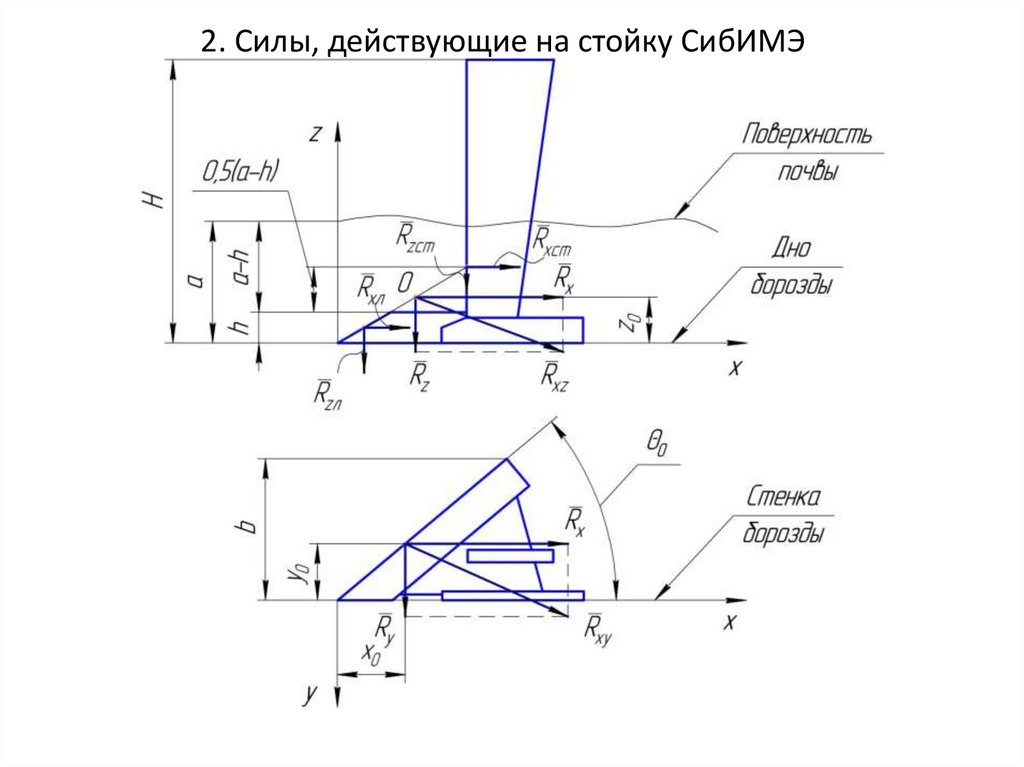
2. Силы, действующие на стойку СибИМЭ11.
Аналогично корпусу плуга, элементарные силы, действующие на стойкуСибМЭ можно привести к главному вектору- силе R, и главному моменту
M
Главный вектор R, задается в виде проекций сил Rx; Ry; Rz на оси X, Y, Z
декартовой системы координат.
2
2
2
Значение вектора R, определяется по выражению: R Rx Ry Rz
Модуль вектора главного момента М можно записать в виде геометрической
суммы величин проекций главного момента на координатные оси:
M Мx 2 Мy 2 Мz 2
Координаты точек приложения главного вектора R определяются по
зависимостям:
x0 0 ,4 b cos
y0 0 ,4 b
z0 0,25 a
12.
Вдоль оси x действует сила Rх. Величина этой силы определяется позависимости:
Rх= Rхл+ Rхст=kab, кН
где Rхл - сила, действующая на лемех, кН;
Rхст – сила, действующая на стойку, кН.
k - удельное сопротивление почвы, кН/м2;
а - глубина обработки почвы, м;
b - ширина захвата корпуса, м.
Вдоль оси y и z действуют соответственно силы:
Ry=cRx;
Rz=dRx
Значения коэффициентов следующие: с=0,15…0,2; d=0,1…0,2.
13.
При известных коэффициентахпримут следующий вид:
Rx
cos R; x
R
Ry
cos R; y
R
c
и
d и силах Rx ,
Ry и Rz косинусы углов
Rx
Rx 2 c 2 Rx 2 d 2 Rx 2
cRx
Rx 2 c 2 Rx 2 d 2 Rx 2
Rz
dRx
cos R; z
R
Rx 2 c 2 Rx 2 d 2 Rx 2
14.
.Определим угол между координатной
, осью x и вектором Rxy – проекцией
главного вектора R на плоскость xy. Для этого воспользуемся зависимостью
cos cos Rxy ; x
Модуль силы : Rxy
Следовательно,
Rx 2 Ry 2
cos cos Rxy ; x
Rx
Rxy
Rx 2 c 2 Rx 2 Rx 1 c 2
Rx
Rx
2
Rxy
Rx 1 c
1
1 c2
Аналогично можно получить значение угла между осью x и проекцией Rxz
главного вектора на плоскость xz:
cos cos( Rxz ; x)
Rx
Rx
1
Rxz Rx 1 d 2
1 d 2
15.
.Проекции моментов Mx, My, Mz определяются по зависимостям аналогично
корпусу плуга
yo
M x
Ry
zo
Rz
xo zo
M y
Rx Rz
xo yo
M z
Rx Ry
16.
Подставив в полученные выражения координаты (xo; yo; zo) точкиприложения главного вектора R и значения Rx , Ry и Rz рассчитаем
величины составляющих Mx, My, Mz главного момента М.
yo
M x
Ry
zo
Rx [0,4 b d 0,25 a c]
Rz
xo
M y
Rx
zo
Rx [0,4 b d cos 0,25 a]
Rz
xo
M z
Rx
yo
Rx (0,4 b c cos 0,4 b)
Ry
17.
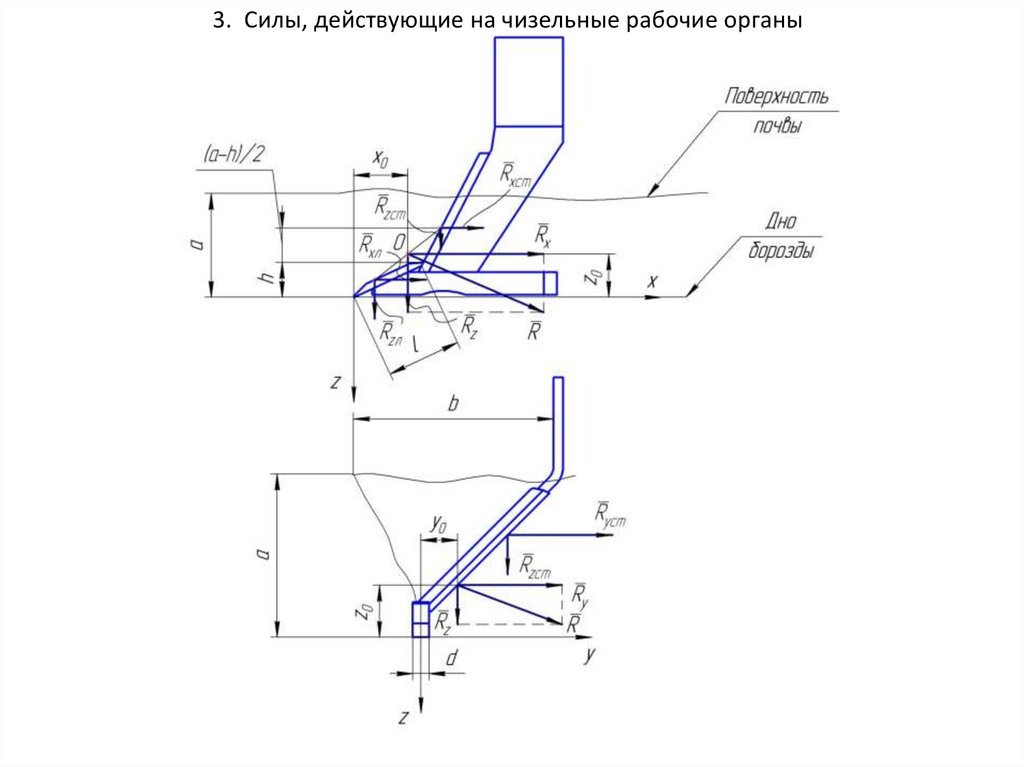
3. Силы, действующие на чизельные рабочие органы18.
Координаты точек приложения главного вектора R определяются позависимостям:
x0 l cos
y0 0,25 a sin
z0 0 ,25 a
Где l - длина долота рабочего органа, м.
β – угол наклона долота к дну борозды, град.
α - угол наклона стойки к дну борозды, град
Расчеты величин главного вектора R и главного момента M
производятся аналогично корпусу плуга
19.
Горизонтальная Rx, вертикальная Rz, и боковая Ry, кНсоставляющие сил, действующих на рабочий орган , определяются
.
по выражениям:
Rх=Rхст+Rхд=kаb;
Rz=Rzст+Rzд=dRх;
Rу=cRх,
где Rхд - сила, действующая на долото, кН;
Rхст – сила, действующая на стойку, кН.
Rzд - сила, действующая на долото, кН;
;
;
Rzст – сила, действующая на стойку, кН.
k - удельное сопротивление почвы, кН/м2;
а - глубина обработки почвы, м;
b - ширина захвата корпуса, м.
где c и d - коэффициенты пропорциональности, равные с=0,2..0,3;
d=0,2…0,4.
20.
.Проекции моментов Mx, My, Mz определяются по зависимостям аналогично
корпусу плуга
yo
M x
Ry
zo
Rz
xo zo
M y
Rx Rz
xo yo
M z
Rx Ry
21.
Подставив в полученные выражения координаты (xo; yo; zo) точкиприложения главного вектора R и значения Rx , Ry и Rz рассчитаем
величины составляющих Mx, My, Mz главного момента М.
yo
M x
Ry
zo
Rx [0,25a sin d 0,25 a c]
Rz
xo
M y
Rx
zo
Rx [l cos d 0,25 a]
Rz
xo
M z
Rx
yo
Rx (l cos с 0,25 a sin )
Ry
22.
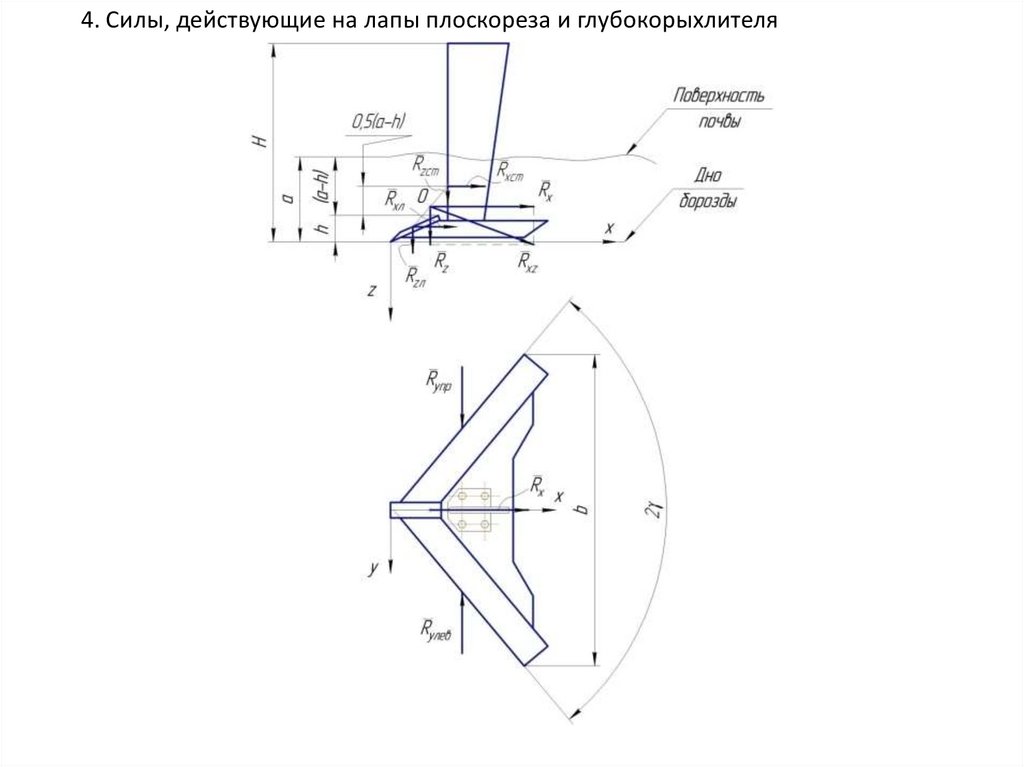
4. Силы, действующие на лапы плоскореза и глубокорыхлителя23.
Координаты точек приложения главного вектора R определяются позависимостям:
x 0 l cos
z 0 (0,25 0,3) a
Где l – длина долота, м;
– угол наклона долота к дну борозды, град.
Расчеты величин главного вектора R и главного момента M
производятся аналогично корпусу плуга
24.
Горизонтальная составляющая сила Rx, кН, определяется по выражению:Rх=Rхст+Rхл=kаb,
где Rхст – сила, действующая на стойку лапы, кН;
Rхл – сила, действующая на лапу, кН;
а – глубина обработки, м;
b – ширина захвата, м;
;
k – удельное сопротивление почвы, кН/м2.
Вертикальная составляющая сила Rz, кН, определяется по выражению:
Rz =dRх,
где d - коэффициент пропорциональности. d = 0.1 0.3
25.
Rупр, Rул – боковые силы, действующие на правую и левую крыльялапы, кН.
Лапа - симметричный рабочий орган, для практических расчетов
принимают Rупр= Rул, и они взаимно уравновешиваются.
26.
.Проекции моментов Mx, My, Mz определяются по зависимостям аналогично
корпусу плуга
yo
M x
Ry
zo
Rz
xo zo
M y
Rx Rz
xo yo
M z
Rx Ry
27.
Подставив в полученные выражения координаты (xo; yo; zo) точкиприложения главного вектора R и значения Rx , Ry и Rz рассчитаем
величины составляющих Mx, My, Mz главного момента М.
yo
M x
Ry
zo
0
Rz
xo
M y
Rx
zo
Rx [l cos d (0,25 0,3) a]
Rz
xo
M z
Rx
yo
0
Ry
28.
Раздел:Тема:
1.
Проектирование орудий
Разработка конструкций рам орудий
Определение количества рабочих органов
29.
Для выбора схемы орудия и расстановки рабочих органов на рамеорудия необходимо определить количество рабочих органов.
При известных значениях тягового усилия трактора Ркр количество рабочих
органов определим по выражению :
Р кр η Δb a k
Ркр η
Δb
n
(b Δb) a k
(b Δb) a k b Δb
Где:
а глубина обработки почвы, м.
k удельное сопротивление почвы, кН/м.
Δb перекрытие рабочих органов, м.
η – коэффициент использования мощности двигателя трактора;
η = 0,95…0,98.
30.
2. Расположение рабочих органов на раме орудияА. Клиновая схема расположения рабочих органов на раме орудия
31.
Схемы орудий вычерчивают в масштабе на листе формата А 3.Для орудий при количестве рабочих органов 6 и менее клиновая схема
расположения рабочих органов, если более 7, то в два ряда – секционное
орудие.
Согласно агротребованиям ширина орудий в транспортном положении
должна быть не более 4,4 м.
32.
33.
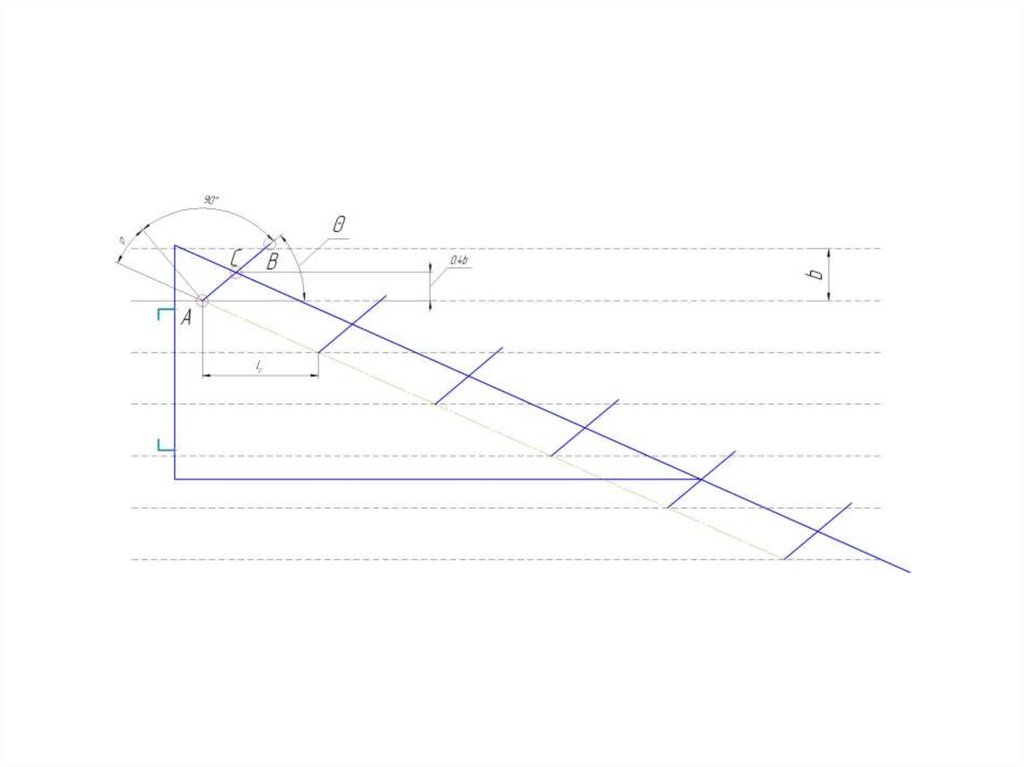
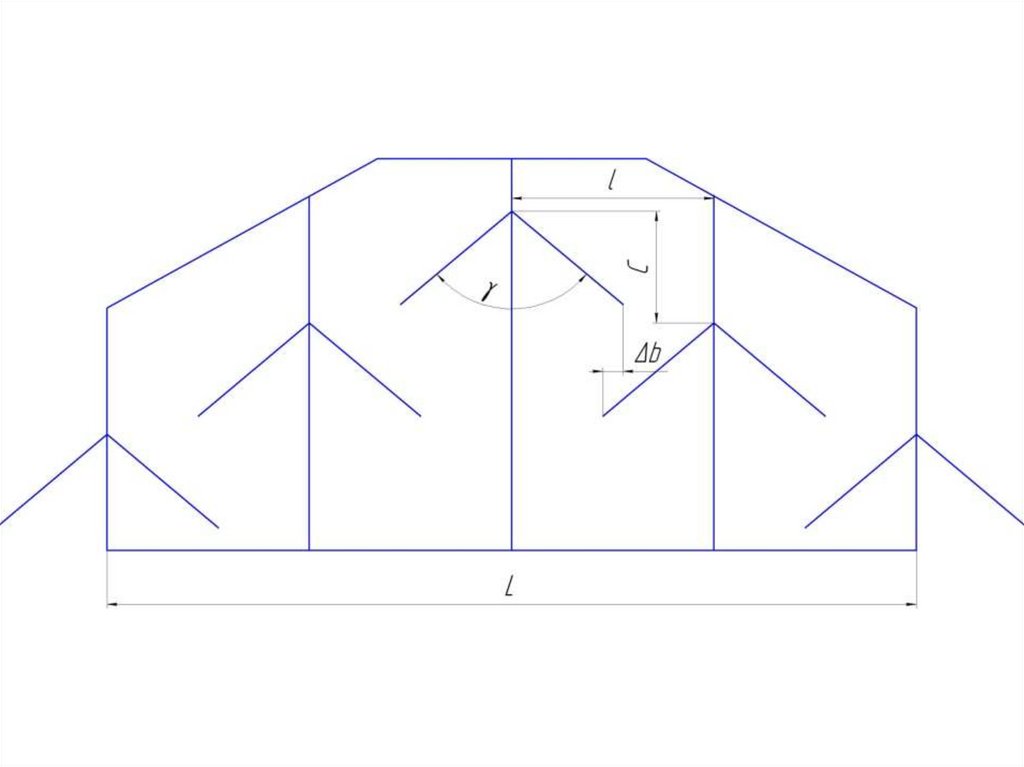
При проектировании орудий расстановку рабочих органов на рамепроизводят в горизонтальной плоскости.
Для этого на расстоянии b проводят z параллельных линий. Z=n+1, где n
– количество рабочих органов.
На второй линии выбираем точку А, из которой под углом θ0 проводим
линию АВ – лезвие лемеха рабочего органа.
К данной линии восстанавливаем перпендикуляр, от которого под углом
φ проводим линию,
которая должна пересечь ранее проведенные параллельные линии.
Точки пересечения данных линий будут носками лемехов последующих
рабочих органов.
Расстояние Lr, м определяется по следующей зависимости:
Lr = b·tg(θ0 + φ)
φ = arctg(f)
f = k·10-2
Для стоек СибИМЭ:
Lrc = Lr – 140
34.
Для чизельных рабочих органов:Lrч = Lr – 160
Продольный брус рамы располагается на расстоянии 0,4b от носка
лемеха и проводится параллельно линии носков лемехов.
Поперечный брус рамы по размеру должен быть таким, чтобы обеспечить
размещение присоединительного треугольника механизма навески орудия.
Поперечный брус располагается перпендикулярно направлению
движения агрегата.
Соединительный брус рамы предназначен для установки опорного
колеса и придания жесткости конструкции рамы.
Располагается перпендикулярно поперечному брусу и соединяется в
крайней левой точке.
35.
36.
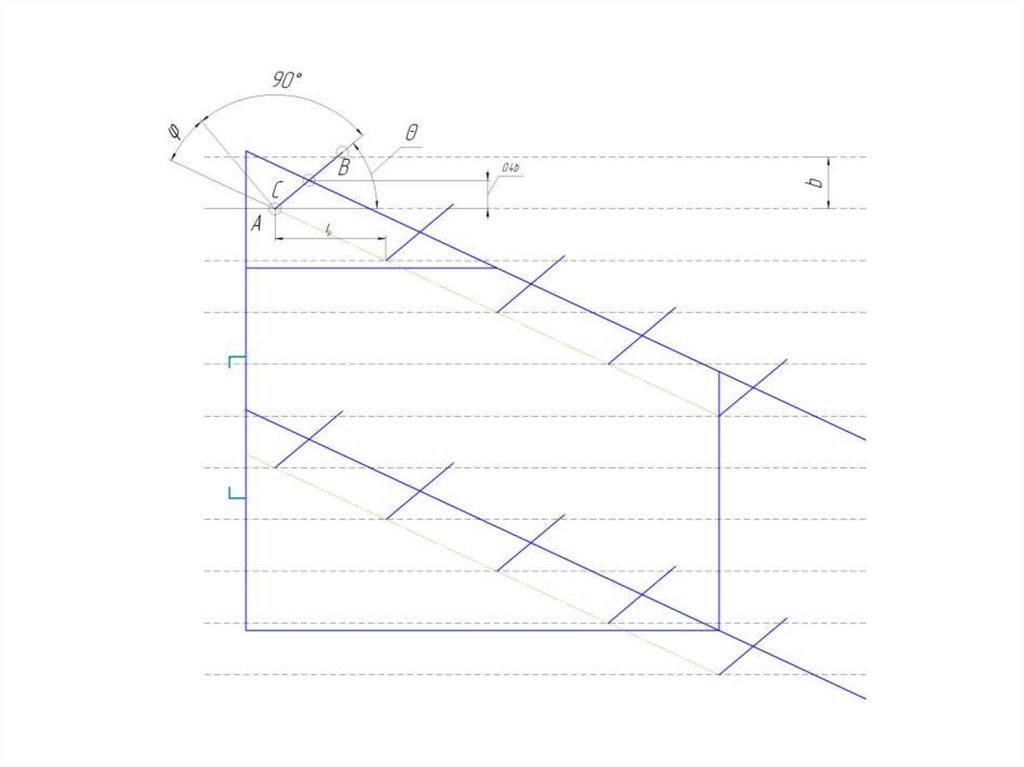
Расстановка рабочих органов на секционных орудиях аналогичнопроизводится в горизонтальной плоскости. На расстоянии b проводят z
параллельных линий. Z=n+1, где n – количество рабочих органов.
На второй линии выбираем точку А, из которой под углом θ0
проводим линию АВ – лезвие лемеха рабочего органа
К данной линии восстанавливаем перпендикуляр, от которого под
углом φ проводим линию, которая должна пересечь ранее
проведенные параллельные линии.
Точки пересечения данных линий будут носками лемехов
последующих рабочих органов для первого ряда.
Для второго ряда данная операция производится аналогично.
Если четное число рабочих органов в первом и втором ряду
располагают одинаковое количество.
Если нечетное число – в первом ряду меньшее число, а во втором
большее количество рабочих органов.
37.
Для рабочих органов стойка СибИМЭ и чизельной расстояние Lrc иLrч определяется аналогично клиновой схемы орудия.
Продольные брусья рамы располагаются на 0,4b от носков лемехов
для каждого ряда.
Длина поперечного бруса рамы выбирается таким
образом, чтобы обеспечить наименьшую консоль продольного бруса
второго ряда.
Соединительный брус второго ряда должен присоединяться
к продольному брусу рамы на расстоянии не более 2,5Lr и служит для
размещения двух опорных колес.
Короткий соединительный брус служит
для размещения одного опорного колеса. Задний брус рамы служит для
придания жесткости конструкции рамы орудия.
38.
• Рамы плоскорезов и глубокорыхлителейимеют два поперечных бруса. На переднем
размещается механизм навески орудия.
Задний служит для придания жесткости.
Между передними и задними брусьями
располагаются продольные брусья, на
которых размещаются рабочие органы.
Число продольных брусьев равно числу
рабочих органов.
39.
40.
41.
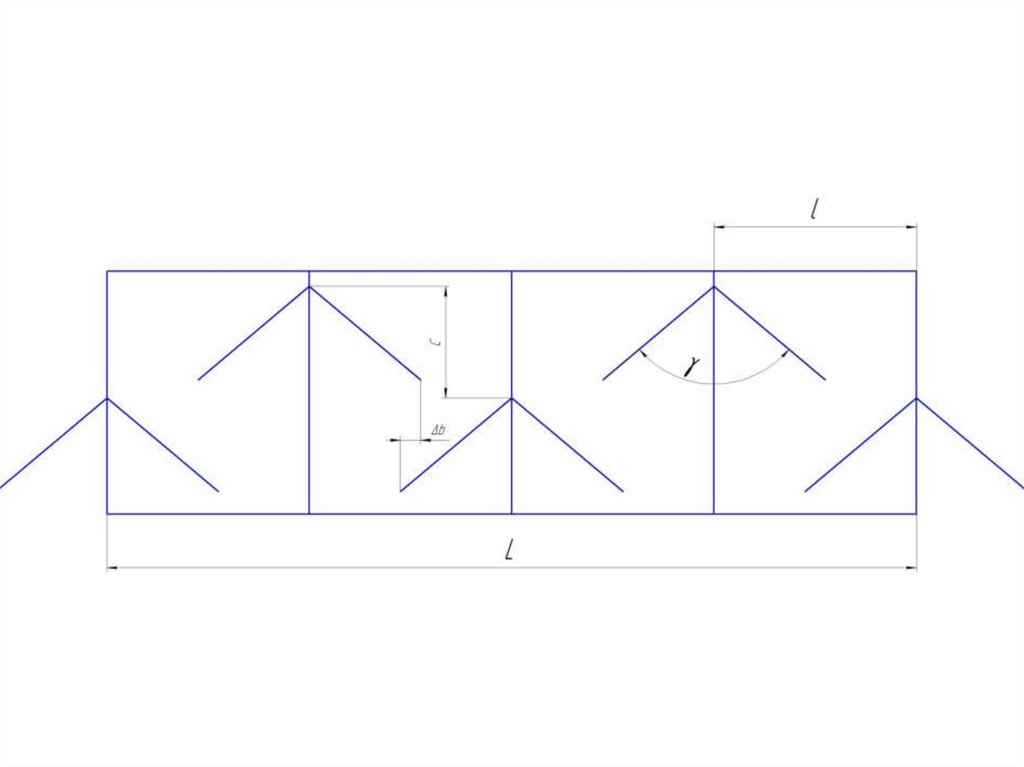
Расстановка рабочих органов на раме плоскорезов иглубокорыхлителей осуществляется в горизонтальной плоскости.
Для этого проводят параллельные линии числом Z на расстоянии Lr.
Z = n,
где n – число рабочих органов.
Lr = b - ∆b,
где b – ширина захвата рабочих органов, м;
∆b – величина перекрытия, м.
В зависимости от количества рабочих органов их располагают:
а) в шахматном порядке – при четном числе рабочих органов;
б) по клиновой схеме – при нечетном числе рабочих органов.
Расстояние смещения рабочих органов по направлению движения
агрегата С определяется С = 0,4-0,6 м.
42.
Плоскорезы и глубокорыхлители симметричные орудия.Для клиновой схемы ось симметрии проходит по первому рабочему
органу.
При шахматном расположении ось симметрии проходит между
вторым и третьим рабочими органами на расстоянии B,м.
В = (b - ∆b)/2.
Рамы плоскорезов и глубокорыхлителей имеют два поперечных
бруса.
На переднем размещается механизм навески орудия.
Задний служит для придания жесткости.
Между передними и задними брусьями располагаются продольные
брусья, на которых размещаются рабочие органы.
Число продольных брусьев равно числу рабочих органов.
43.
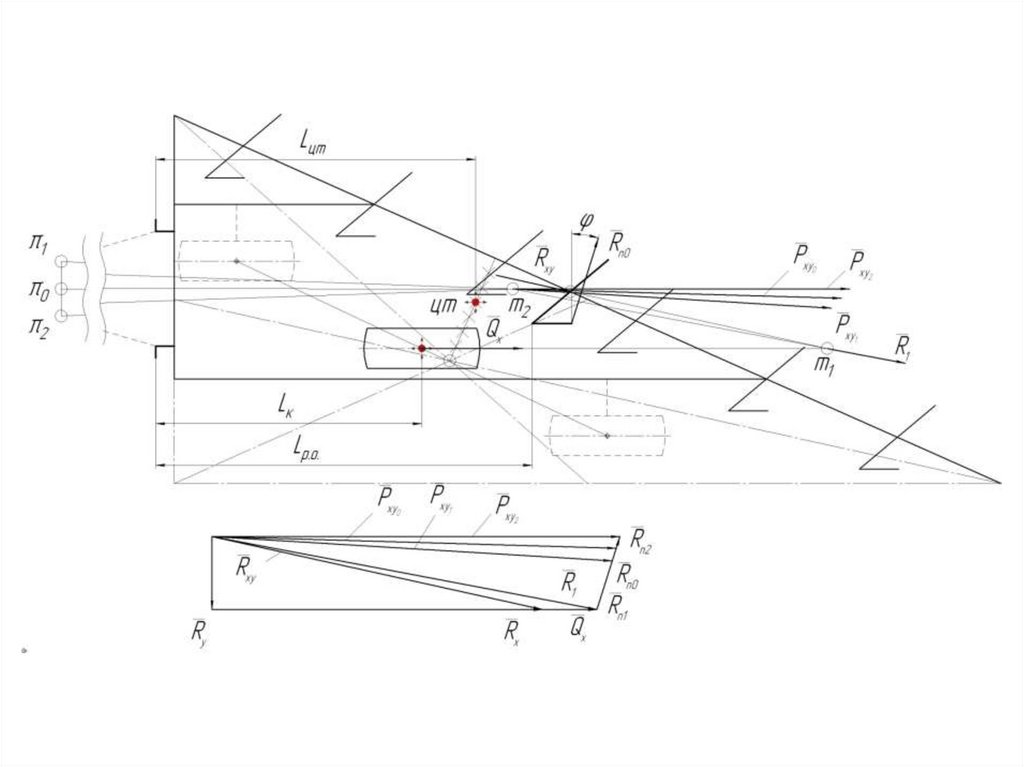
Выбор линии тяги трактора в горизонтальной плоскостиЛиния тяги трактора в горизонтальной плоскости определяется
графическим способом.
Для этого построим в масштабе горизонтальную проекцию плуга и
положение МЦВ механизма навески трактора
Длина нижних продольных тяг трактора выбирается по таблице
Значение силы Rxyо , действующей на орудие, определяют по
выражению
Rxyо = Rxyi,
где - Rxyi - горизонтальная составляющая сил, действующих на рабочий
орган.
Сила Rxyо приложена к среднему или условно среднему корпусу
плуга на расстоянии l = 0.4b.
Общая сила Rnо , действующая на полевые доски:
Rnо = Rni ;
Rnо направлена под углом φ и приложена к концу полевой доски,
где tg φ = f; f = k*10-2
44.
45.
Горизонтальная составляющая сил, действующих на опорноеколесо:
Qx =Q ∙ tg μ,
где μ = 9 – 12 0 ; tg μ =0.1 – 0.3.
Для определения направления линии тяги построим силовой
многоугольник в масштабе.
Для этого выбираем полюс, откладываем силы Rxyо и Qx и
получаем результирующую силу R1.
Точка приложения силы R1 находится на пересечении
продолжения сил Rxyо и Qx.
R1 переносим в точку 1.
Из точки 1 проводим продолжение линии действия силы R1 до
пересечения с продолжением действия Rпо и получаем точку 2 – точку
сопротивления орудия.
Точку 2 соединяем с МЦВ и получаем .
46.
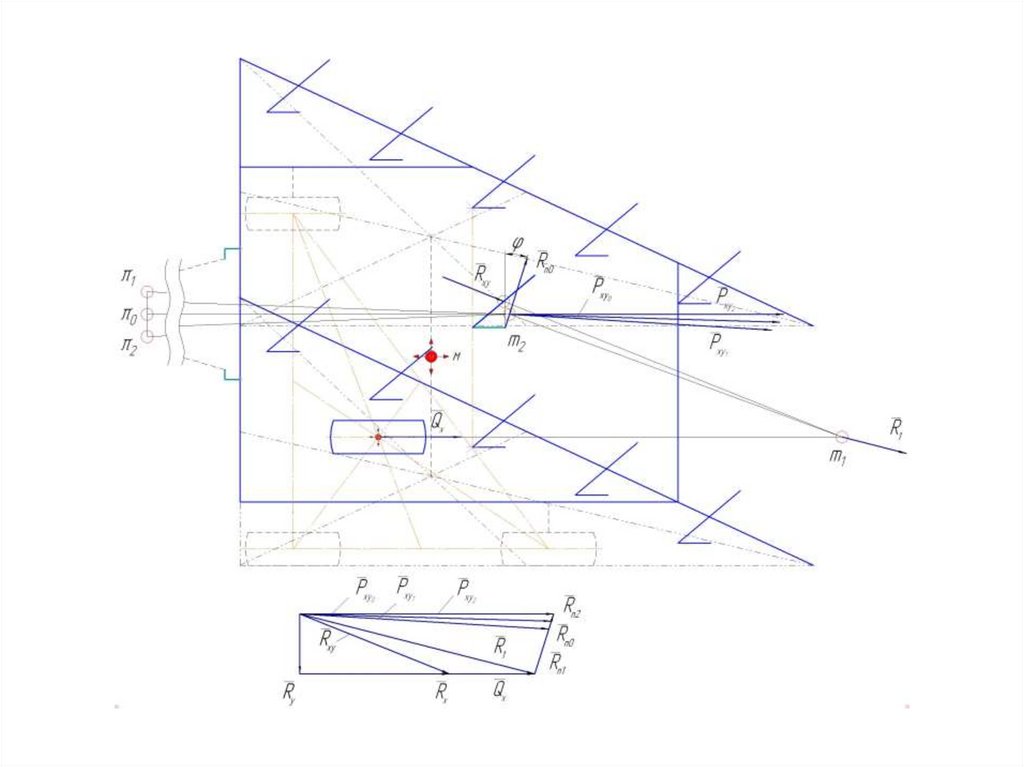
Линия - 2 определяет направление силы Pxy – тяговогосопротивления плуга в горизонтальной плоскости.
Для этого из начала вектора R1 проведем линии, параллельные 2 , а из конца вектора R1 проведем линию, параллельную Rпо.
Точка пересечения данных линий даст нам положение концов
векторов сил Pxy и Rпо.
Передвинем механизм навески по поперечному брусу рамы и
определим значение Pxy для других условий.
Как видим, Pxy увеличивается и соответственно увеличивается Rп0,
но при этом необходимо следить, чтобы значение силы Р, полученное
при работе 5 в продольно-вертикальной плоскости, равнялось
значению Pxy, полученному в горизонтальной плоскости, то есть P =
Pxy.
Таким образом, мы добьемся наибольшей устойчивости плуга в
горизонтальной плоскости.
При работе многокорпусных плугов с меньшим количеством
корпусов необходимо определить положение механизма навески плуга
на поперечном брусе рамы.
Аналогичным способом и подготовить отверстия или места
крепления для навески для –1 и –2. Это позволяет агрегатировать
данные орудия с тракторами другого колеса тяги.
47.
48.
Определениеплоскости
линии
тяги
трактора
продольно-вертикальной
Для этого необходимо построить многоугольник сил.
Данный многоугольник сил необходим для определения усилия Q на
ободе опорного колеса для дальнейшего конструктивного расчета рамы
орудия, выбора механизма регулировки глубины хода рабочих органов и
типа опорных колес.
При этом необходимо учитывать, что результирующая сила P должна
проходить через МЦВ механизма навески трактора, который располагается
в окрестностях центра тяжести трактора. Из этого условия определяется
точка присоединения центральной тяги на раме орудия.
Величина звена 9 - 5 должна быть такой, чтобы находился в
окрестностях центра тяжести трактора.
49.
50.
51.
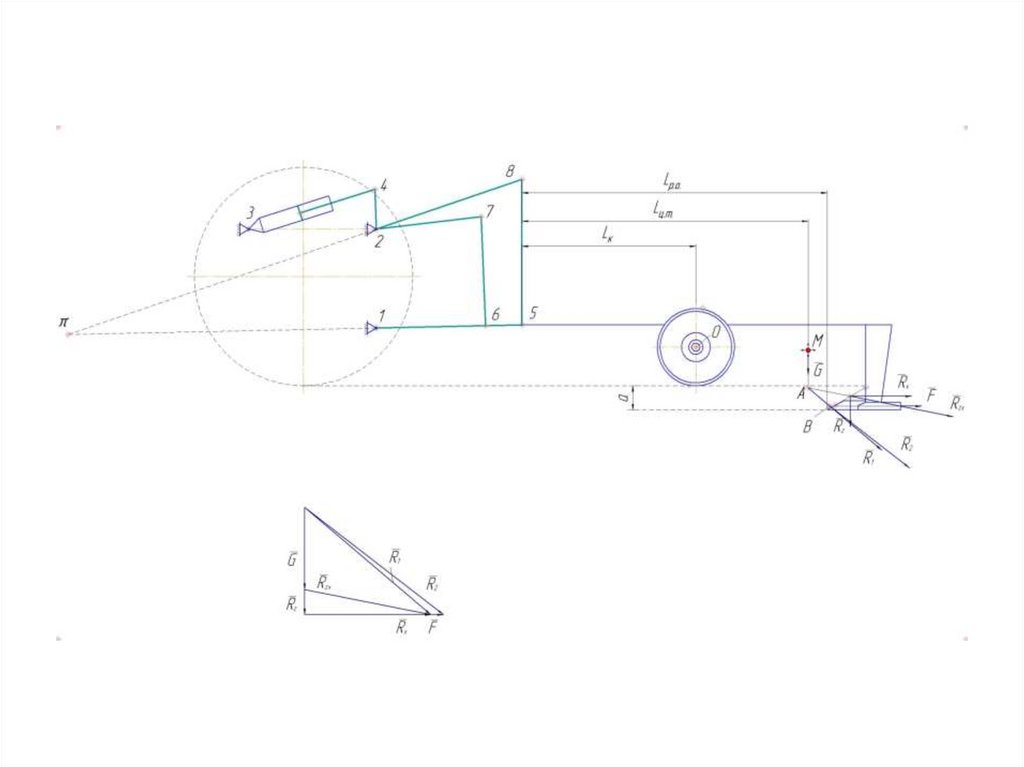
На условно средний или средний рабочий орган прикладываем силу F –трения полевых досок о почву, а в Ц.Т. силу G.
Выбираем масштаб и производим построение силового многоугольника.
Вначале откладываем силу G , затем Rz и силу Rx.
Соединяя начало вектора Rz с концом вектора Rx получаем вектор Rxz.
Переносим параллельно Rxz в точку приложения на рабочий орган.
Соединяя полюс плана сил с концом вектора Rxz получаем вектор R1.
Точкой приложения силы R1 будет точка А. В неё параллельно переносим
вектор силы R1.
Откладываем силу F на силовом многоугольнике и получаем вектор силы R2.
Точкой приложения силы R2 будет точка В.
В неё переносим вектор силы R2.под тем же углом наклона к горизонту на
схему орудия.
52.
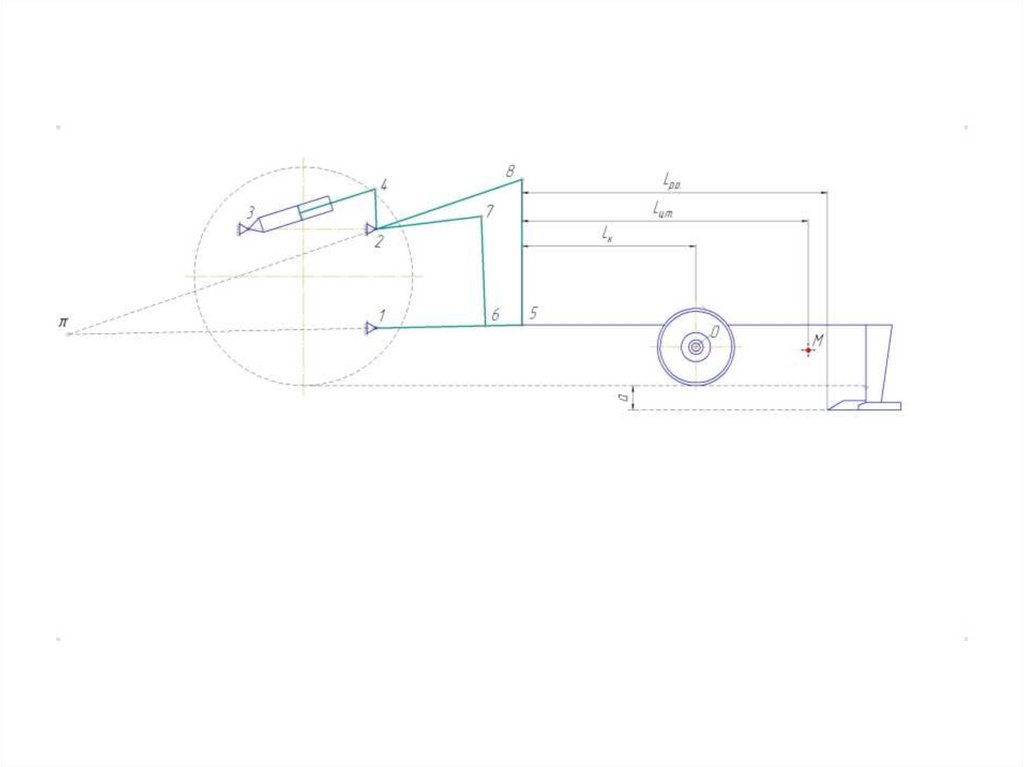
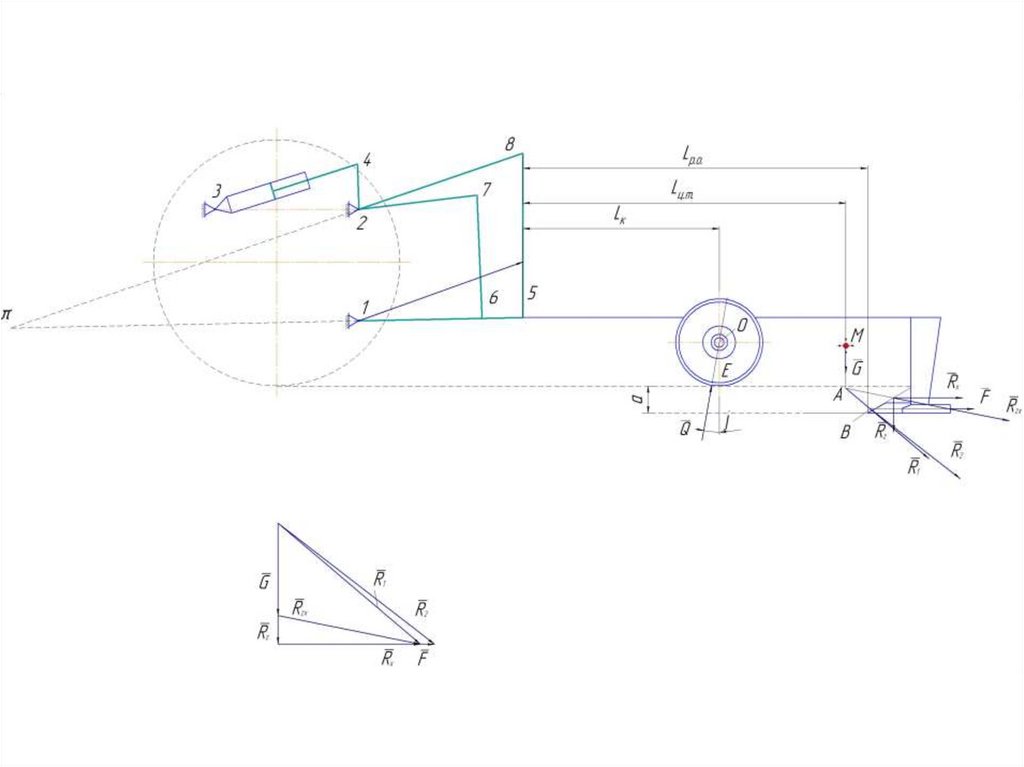
А. Определение реакции на ободе опорного колесаНавесное орудие соединяется с трактором с помощью механизма навески.
Мгновенный центр вращения механизма навески
пересечении продолжений звеньев 1 —5 и 2—9.
находится
на
Реакцию почвы на опорное колесо определяют из
уравнения
моментов всех сил, действующих на плуг, относительно мгновенного
центра вращения навесной машины .
Мы будем определять усилие Q построением совмещенного плана
с механизмом навески трактора.
За полюс плана скоростей примем точку 1 крепления нижних тяг на
тракторе, а вектор скорости точки 5 расположим вдоль звена 1-5.
При этом масштаб следует задать таким образом, чтобы длина вектора
скорости точки 5 равнялась длине звена 1-5.
53.
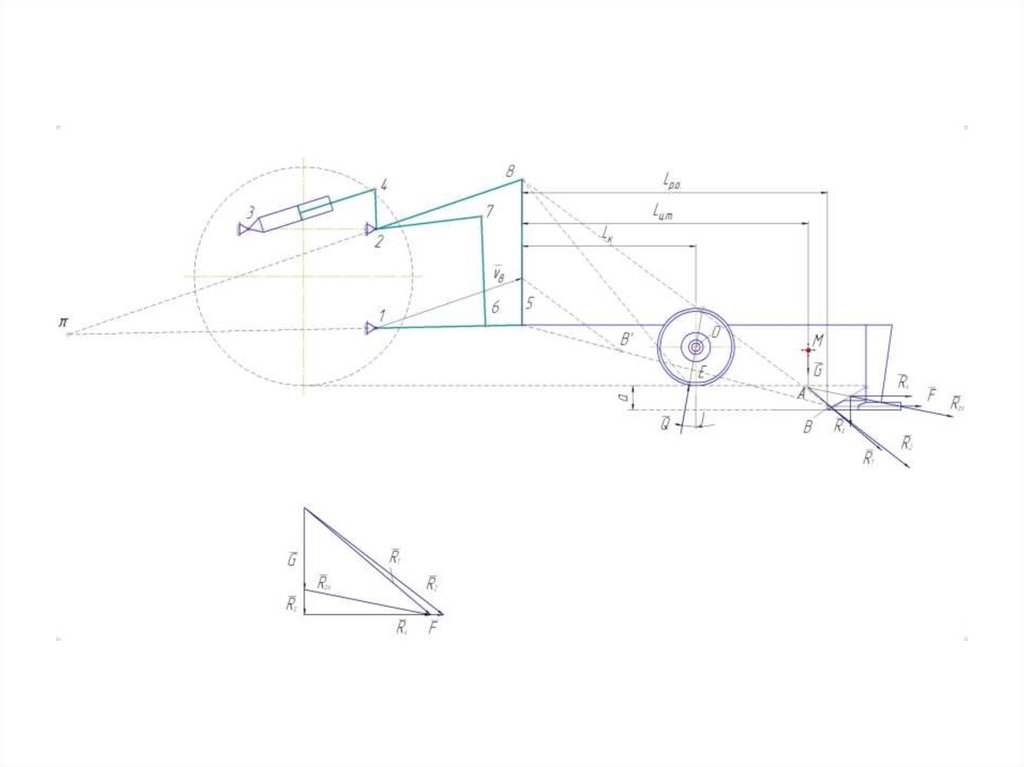
Чтобы определить скорость точки 9, на плане скоростей необходимопровести линию 1 —9’, параллельную звену 2—9.
Вектор скорости точки 9 будет располагаться именно по направлению
звена 2—9.
Кроме этого, известно, что
\/9=\/5+V9-5 т. е. вектор скорости точки 9
можно рассматривать как сумму векторов скорости точки 5 и скорости
точки 9 относительно точки 5.
Вектор V9-5 будет располагаться вдоль звена 58—9. Поэтому точка 9’
пересечения линии1 —9’ с линией действия V9-5 и определит значение \/9.
54.
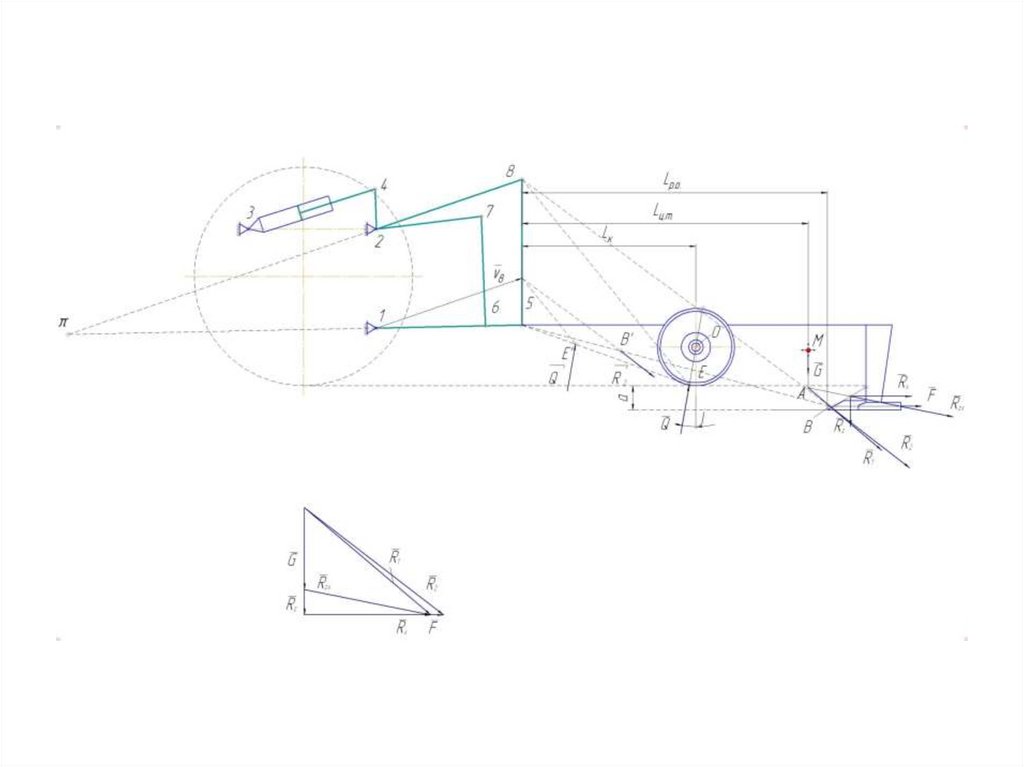
55.
Далее необходимо построить векторы скоростей точек приложения Q и R2.Учитывая, что эти силы приложены к деталям, жестко связанным со звеном
5—9, скорости конечных точек которого определены, можно
воспользоваться методом подобия
Для этого соединим точку В с точками 5 и 9 и из конца вектора скорости V9
проведем линию 9'-В', параллельную 9-В.
Точка пересечения этих линий позволит определить конец вектора
скорости точки В.
56.
57.
Аналогично находят и вектор скорости точки Е.Согласно теореме Н. Жуковского, векторы силы R2 и Q следует
перенести параллельно самим себе в одноименные точки плана скоростей
(обозначим на плане скоростей силы Q и R2 через Q' и R2’).
58.
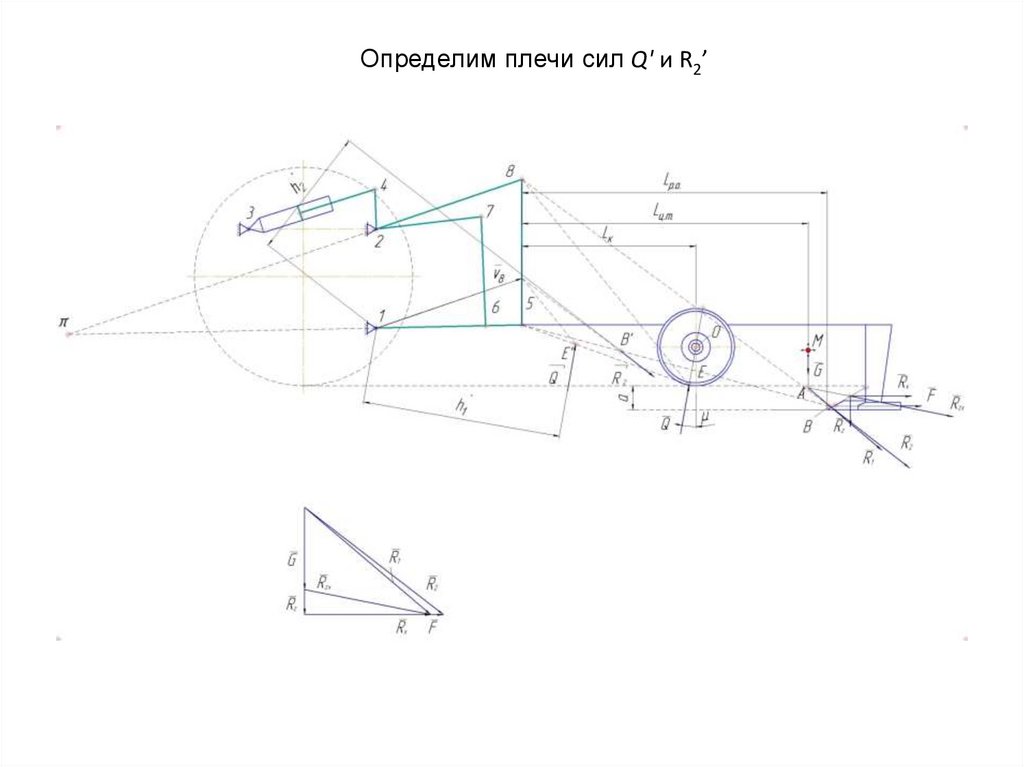
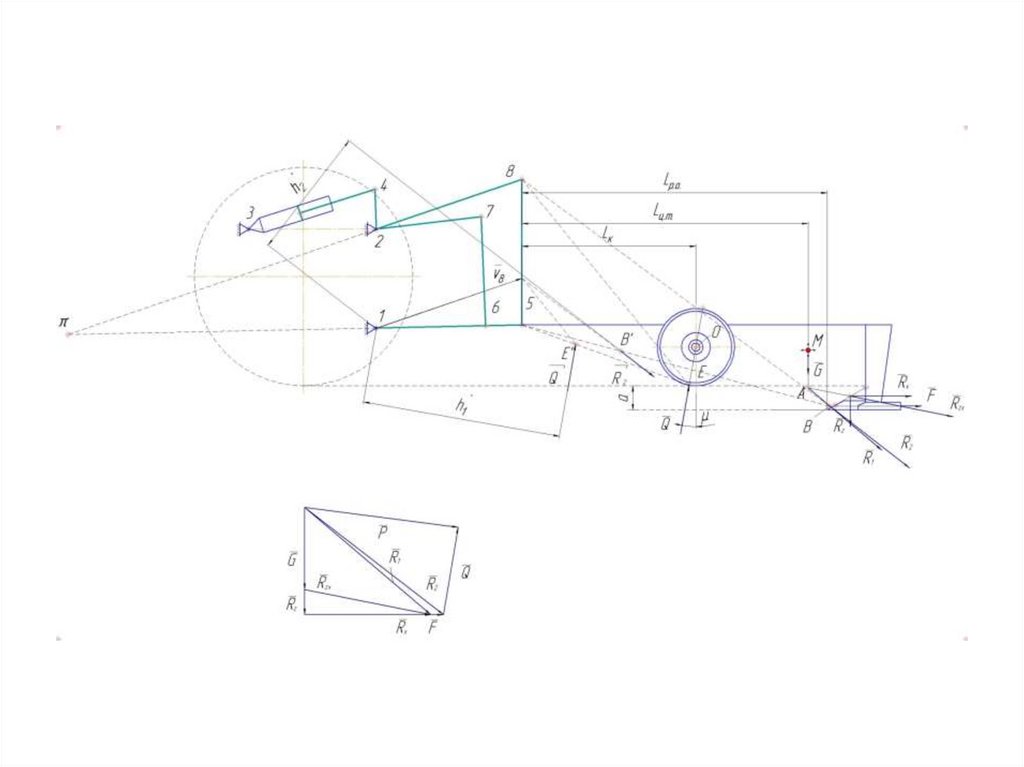
59. Определим плечи сил Q' и R2’
60.
Сумма моментов сил Q' и R2’ относительно полюса плана (точка π)будет равна нулю:
M R '2 h '2 Q' h '1 0
откуда:
R2 ' h2 '
Q' Q
h1 '
Зная числовое значение силы Q откладываем в масштабе её значение
на силовом многоугольнике.
Соединяем полюс и конец вектора силы Q получим результирующую силу Р.
Сила Р должна проходить через МЦВ механизма навески трактора.
61.
62.
Определение диаметра опорных колес орудия,
Для определения диаметра колеса Dk,
Грандвуанэ-Горячкина:
м, обычно используют формулу
Qz
Dk
q в0 3
где во - ширина обода опорного колеса, м;
Qz -вертикальная нагрузка на опорное колесо, кН;
q - коэффициент объемного сопротивления почвы деформации,
кН/м3;
- коэффициент перекатывания колеса.
Связь между диаметром Dk, м, шириной обода во, м, вертикальной
нагрузкой на колесо Qz кН и тяговым сопротивлением на его
перекатывание Qх, кН, устанавливается формулой ГрандвуанэГорячкина:
2
Dk
и соотношением
Qz
qв0Qx3
Qz
в0
k
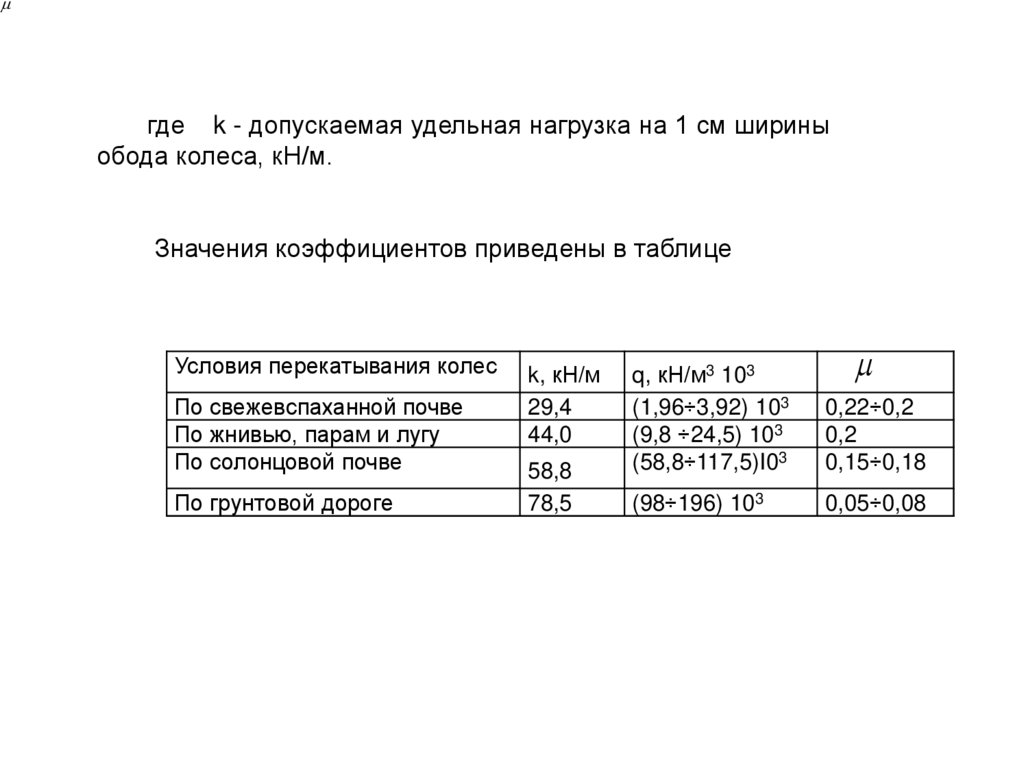
63.
где k - допускаемая удельная нагрузка на 1 см шириныобода колеса, кН/м.
Значения коэффициентов приведены в таблице
Условия перекатывания колес
По свежевспаханной почве
По жнивью, парам и лугу
По солонцовой почве
По грунтовой дороге
k, кН/м
29,4
44,0
58,8
78,5
q, кН/м3 103
(1,96÷3,92) 103
(9,8 ÷24,5) 103
(58,8÷117,5)I03
0,22÷0,2
0,2
0,15÷0,18
(98÷196) 103
0,05÷0,08
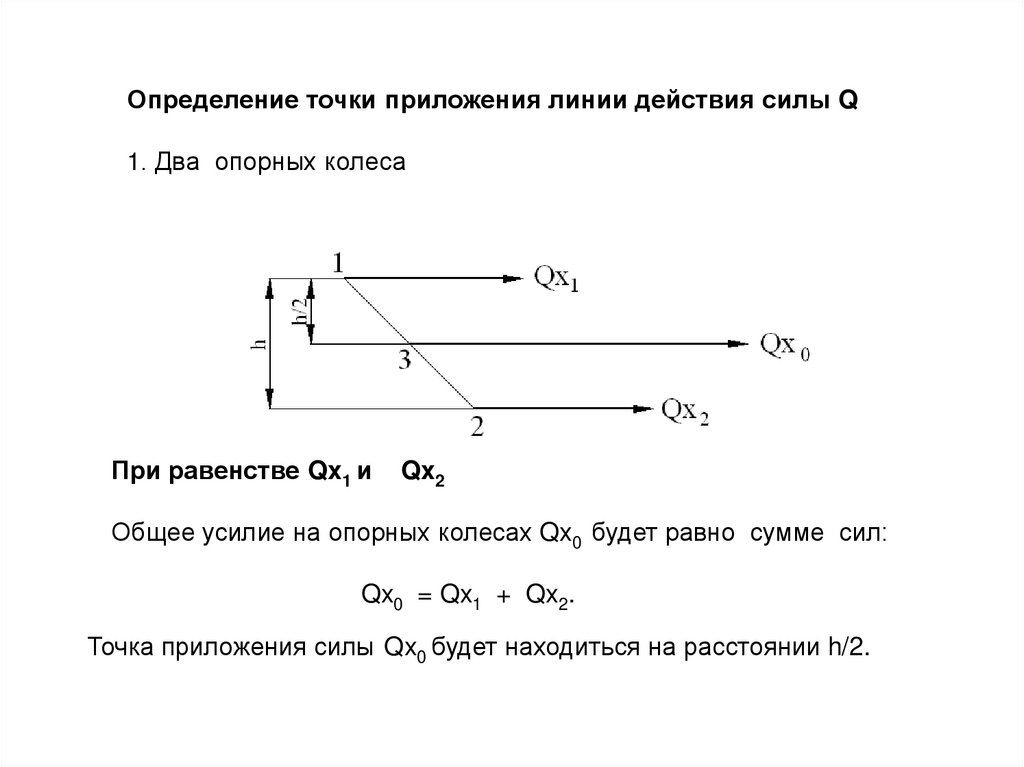
64.
Определение точки приложения линии действия силы Q1. Два опорных колеса
При равенстве Qx1 и
Qx2
Общее усилие на опорных колесах Qx0 будет равно сумме сил:
Qx0 = Qx1 + Qx2.
Точка приложения силы Qx0 будет находиться на расстоянии h/2.
65.
.При условии неравенства сил Qx1 и Qx2, то есть Qx1 ≠ Qx2,
Общее усилие на опорных колесах Qx0 будет также равно сумме сил:
Qx0 = Qx1 + Qx2.
Для определения точки приложения силы Qx0 составим уравнение
моментов сил относительно точки 1,
при этом Qx0 должна быть со знаком минус; тогда уравнение
моментов будет иметь вид
М1 = Qx2 h – Qx0 x = 0.
Отсюда определяем расстояние х до точки приложения силы Qx0:
Qx2 h
x
Qx0
66.
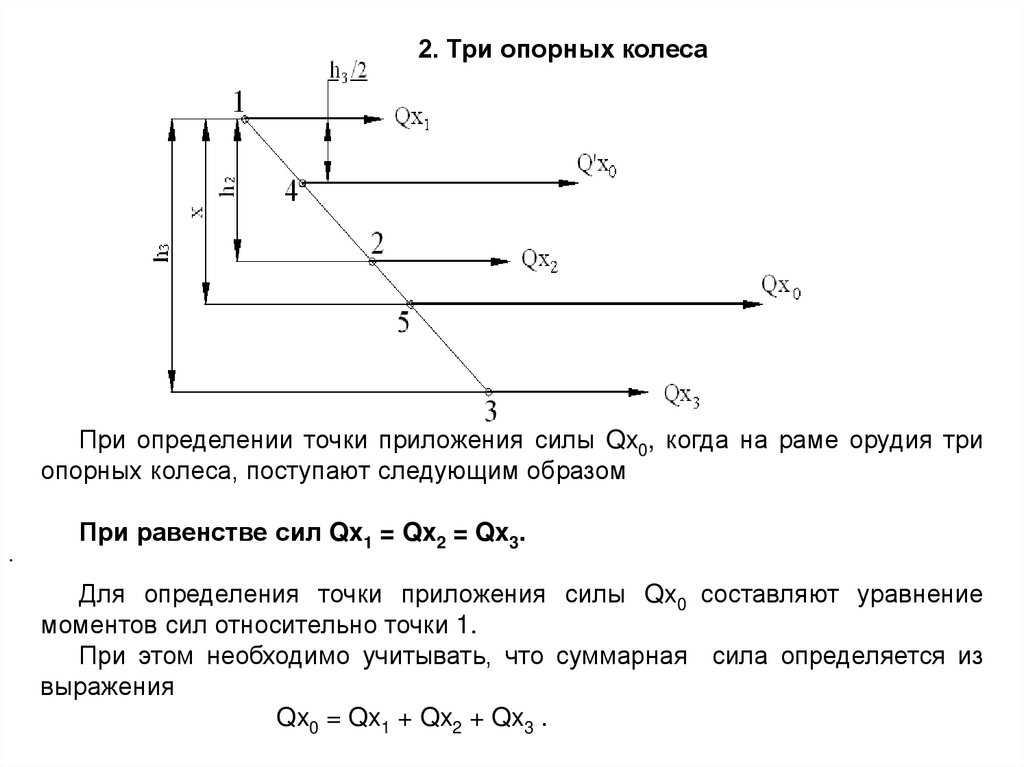
2. Три опорных колесаПри определении точки приложения силы Qx0, когда на раме орудия три
опорных колеса, поступают следующим образом
.
При равенстве сил Qx1 = Qx2 = Qx3.
Для определения точки приложения силы Qx0 составляют уравнение
моментов сил относительно точки 1.
При этом необходимо учитывать, что суммарная сила определяется из
выражения
Qx0 = Qx1 + Qx2 + Qx3 .
67.
Её значение должно быть со знаком минус;будет иметь вид
М1 = Qx2 h2 + Qx3 h3 – Qx0 x = 0,
отсюда находим значение плеча данной силы:
x
уравнение моментов
Qx2 h2 Qx3 h3
Qx0
При неравенстве сил Qx1 Qx2 Qx3
Точку приложения определяют следующим образом:
сначала определяют положение силы Qx’0:
Qx’0 = Qx1 + Qx2.
Точка приложения силы Qx’0 (точка 4) определяется аналогично двум
опорным колесам.
Затем определяют точку приложения силы Qx0; числовое значение
которой
Qx0 = Qx’0+ Qx3.
Точка приложения силы Qx0 (точка 5) определяется так же, как и для
силы Qx’0.
68.
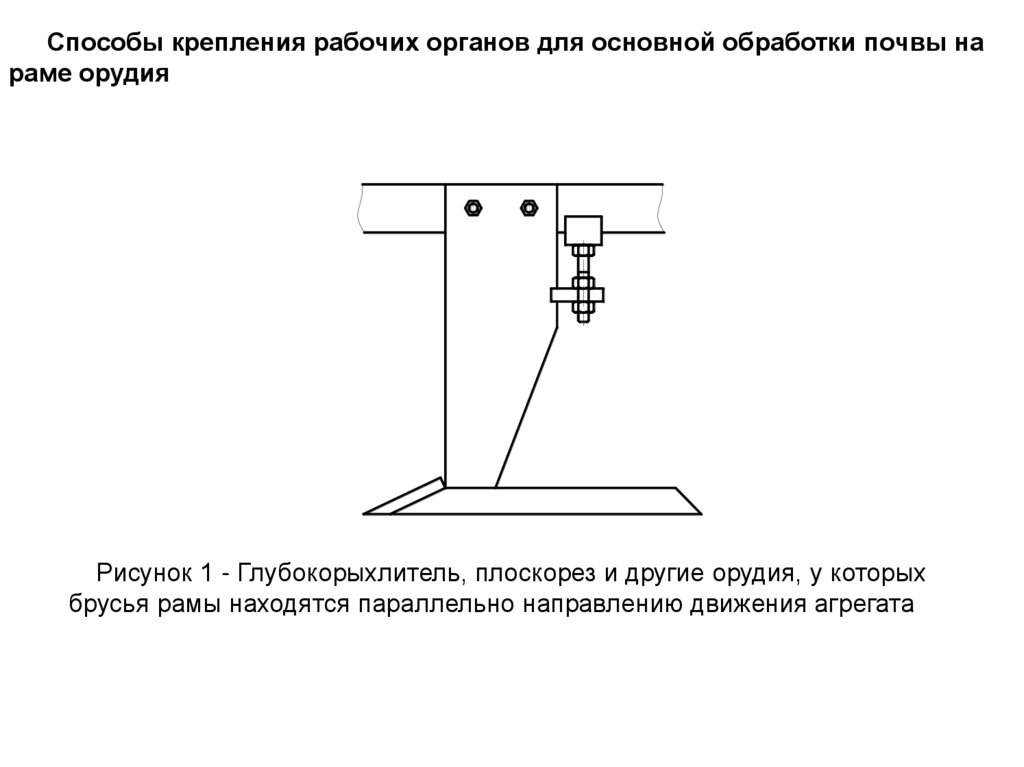
Способы крепления рабочих органов для основной обработки почвы нараме орудия
Рисунок 1 - Глубокорыхлитель, плоскорез и другие орудия, у которых
брусья рамы находятся параллельно направлению движения агрегата
69.
A-AA
A
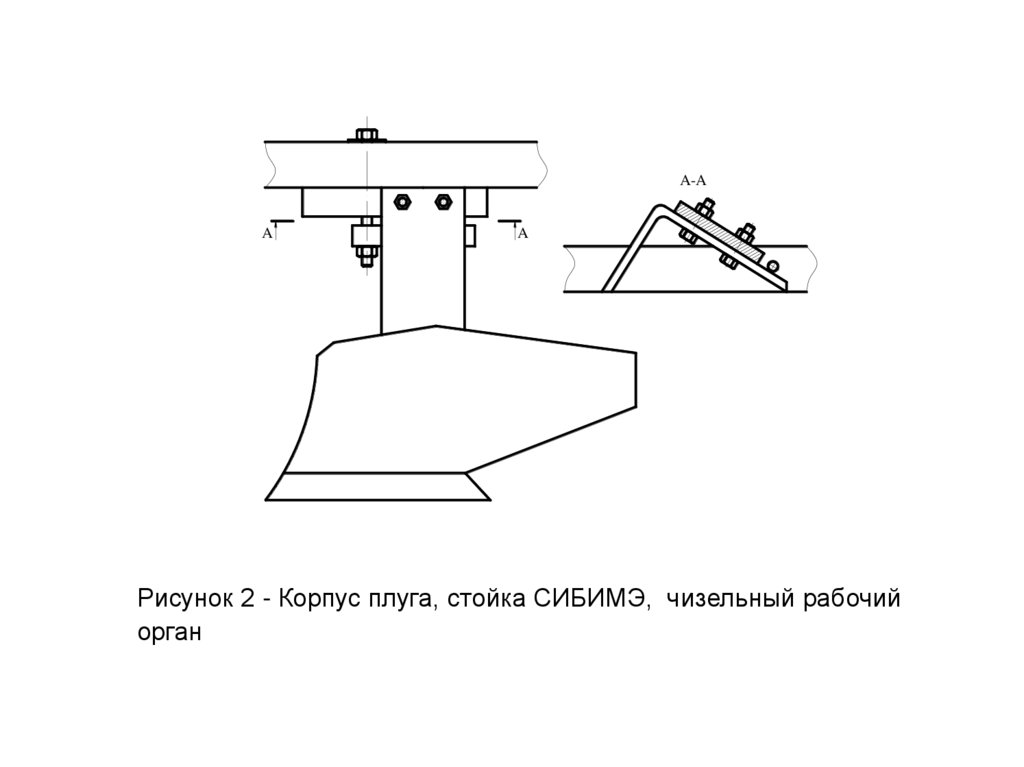
Рисунок 2 - Корпус плуга, стойка СИБИМЭ, чизельный рабочий
орган















































 industry
industry








