Лучистый теплообмен. (Лекция 14)

1.

Лекции по ОТТМО
доцент каф. Э6, ктн Рыжков С.В.
Э6
нергомашиностроение.
Лекция №14
ЛУЧИСТЫЙ ТЕПЛООБМЕН
•Основные понятия и определения
•Основные законы лучистого теплообмена
•Различные случаи теплообмена излучением
•Радиационный теплообмен между произвольно расположенными
элементами поверхностей нагрева
•Интегральные характеристики излучения и
поглощения полупрозрачного объема
•Радиационный теплообмен в газах
•Радиационный теплообмен между газом и оболочкой

2.

Основные понятия и определения
Энергия теплового излучения возникает в теле вследствие тепловой энергии и представляет
собой электромагнитные колебания.
Рис. 1. Реакция тела на тепловое
излучение
Космическое излучение
γ-излучение
Рентгеновские лучи
Ультрафиолетовые лучи
Видимые (световые) лучи
Тепловые лучи
Электромагнитные волны
0,05 • 10-9 мм
(0,5 ... 10) • 10-9
10-9 .. .2 • 10-5
2 • 10-5... 0,4 • 10-3
(0,4... 0,8) • 10-3
0,8 • 10-3 ... 0, 8
2 • 105
Если из общего количества энергии Q, падающего на тело, поглощается QA, отражается QR и
проходит сквозь тело QD (рис. 1), то Q = QA + QR + QD . Отношение QA / Q = А называют
поглощателъной способностью, отношение QR / Q = R — отражательной способностью и
отношение QD / Q = D — пропускной способностью тела.
Следовательно, А + R + D = 1.
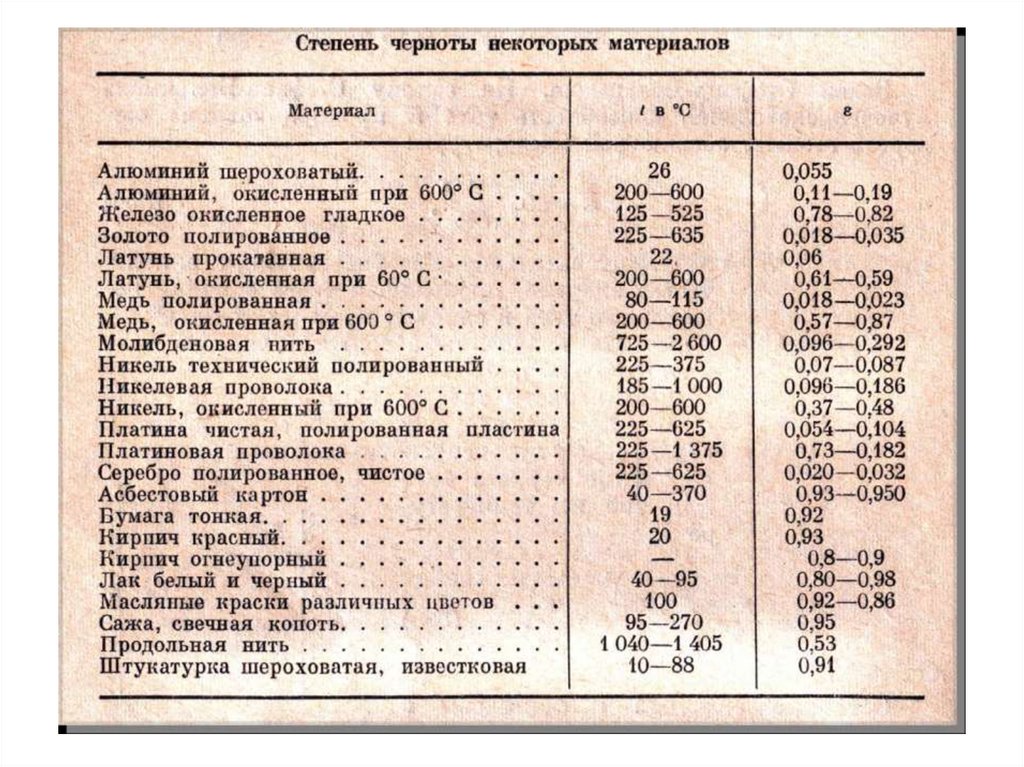
Если А = 1, R = 0, D = 0 - тело абсолютно черное, так как вся энергия поглощается телом. А = 0,96 имеют
шероховатые тела, покрытые сажей.
Если R = 1, A = 0, D = 0 - падающее на тело излучение полностью отражается. Этот предельный случай является
абстракцией. Такое абстрактное тело, создающее рассеянное диффузное отражение, называется абсолютно белым,
а тело, отражающее по законам геометрической оптики, называется зеркальным.
При D = 1, R = 0, A = 0 тело совершенно прозрачно (диатермично) для теплового излучения и вся энергия проходит
через тело.
В природе абсолютно черных, прозрачных, белых и зеркальных тел нет. Тела, поглощательная способность которых от
длины волны не зависит, называют серыми.

3.

Закон Стефана-Больцмана
По закону Стефана-Больцмана лучеиспускательная способность тела Е пропорциональна
четвертой степени абсолютной температуры:
T
E C0
100
4
(1)
Е — лучеиспускательная способность тела, т. е. количество энергии, проходящей через единицу
поверхности тела в единицу времени, Вт/м2;
С0 = 5,67 — константа излучения абсолютно черного тела, Вm/(м2 • K4);
ε — степень черноты тела, характеризующая собой отношение лучеиспускательной способности Е
серого тела к лучеиспускательной способности Е0 абсолютно черного тела при той же температуре Т
4
T
C
E
100
C
4
E0
C0
T
C0
100
(2)

4.

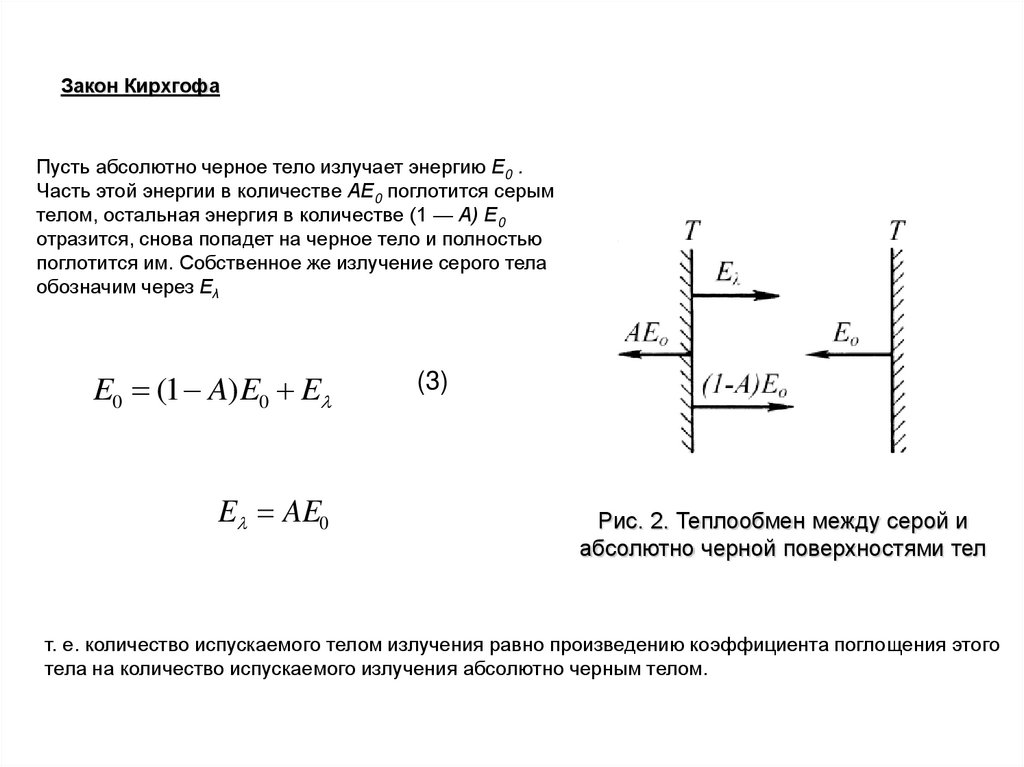
Закон Кирхгофа
Пусть абсолютно черное тело излучает энергию Е0 .
Часть этой энергии в количестве АЕ0 поглотится серым
телом, остальная энергия в количестве (1 — А) Е0
отразится, снова попадет на черное тело и полностью
поглотится им. Собственное же излучение серого тела
обозначим через Еλ
E0 (1 A) E0 E
E AE0
(3)
Рис. 2. Теплообмен между серой и
абсолютно черной поверхностями тел
т. е. количество испускаемого телом излучения равно произведению коэффициента поглощения этого
тела на количество испускаемого излучения абсолютно черным телом.

5.

6.

Закон Ламберта
Общее количество энергии, излучаемой по всем
направлениям в пределах полусферы с 1 м2
поверхности в единицу времени, равно
лучеиспускательной способности
T
E C0
100
Рис. 3. Излучение с элементарной
площадки на поверхности тела
4
Если же рассматривать излучение тела лишь в
направлении нормали Еn, то известно, что оно
будет в = 3,14 раз меньше
Закон Ламберта справедлив для абсолютно
черных тел, для серых же тел он справедлив
при φ <= 60°.
Величина F12 м2, называется взаимной
поверхностью излучения. Она является чисто E
геометрическим параметром, который
определяется размерами и формой поверхностей
тел, их взаимным расположением и расстоянием
между ними:
En
E
E En cos
(4,5)
4
T
C0
E
100 cos
En cos cos
(6)
cos 1 cos 2
'
F12 dF1
dF
dF1 12 F1
2
2
r
F1
F2
F1
Величины φ' и φ12 представляют собой соответственно локальный и средний угловые коэффициенты.
Численное значение φ ' показывает, какая доля энергии, излучаемой элементом dF1 по всему
полупространству, попадает на поверхность F2. Значение же φ12 является осредненным значением φ' по всей
поверхности F1.

7.

Закон Планка
Излучение называется монохроматическим, если оно отвечает какой-либо определенной длине
волны. Излучение, отвечающее длинам волн от 0 до ∞, называется интегральным.
Планком теоретически установлена зависимость интенсивности излучения абсолютно черного
тела I от длины волны и температуры:
dE C1 5
I
C2
1
d
T
e
Вт
м3
(7)
λ — длина волны излучения в м;
Т — абсолютная температура в ° К;
С1 и С 2 — постоянные величины;
С1 = 3,74 10 –16 Вт/м2 и С2 = 1,438 10-2 м*К
– постоянные закона Планка
е — основание натуральных логарифмов.
Закон Вина
Закон «смещения» Вина вытекает из закона Планка и
устанавливает зависимость длины волны λт ,
соответствующей максимальной интенсивности, от
температуры:
Рис. 4. Зависимость интенсивности
излучения от длины волн и температуры
mT 2,9 ( мм град)

8.

Различные случаи теплообмена излучением
Лучистый теплообмен между двумя телами
n
T1 T2
Qл nC0
F1
100
100
4
4
Учёт солнечного излучения
T1 4 T2 4
Qл 1C0 F1
A1( s ) F0 Es
100 100
1
1 F1 1
1
1 F2 2
W
e
4 r 2
ккал
м 2ч
Теплообмен между газом и поверхностью твёрдого тела
Tг
Tст
q 5, 69 э г
Aг
100
100
4
nр
1
1
1
1
1
2
4
Если степень черноты стенки εст=0.7..1
пр
ст
1
э ст
2
г ст
г (1 ст )
г CO ( pCO l , Tг ) H O ( pН Ol , Tг ) г
2
2
2
2

9.

Радиационный теплообмен между произвольно расположенными
элементами поверхностей нагрева
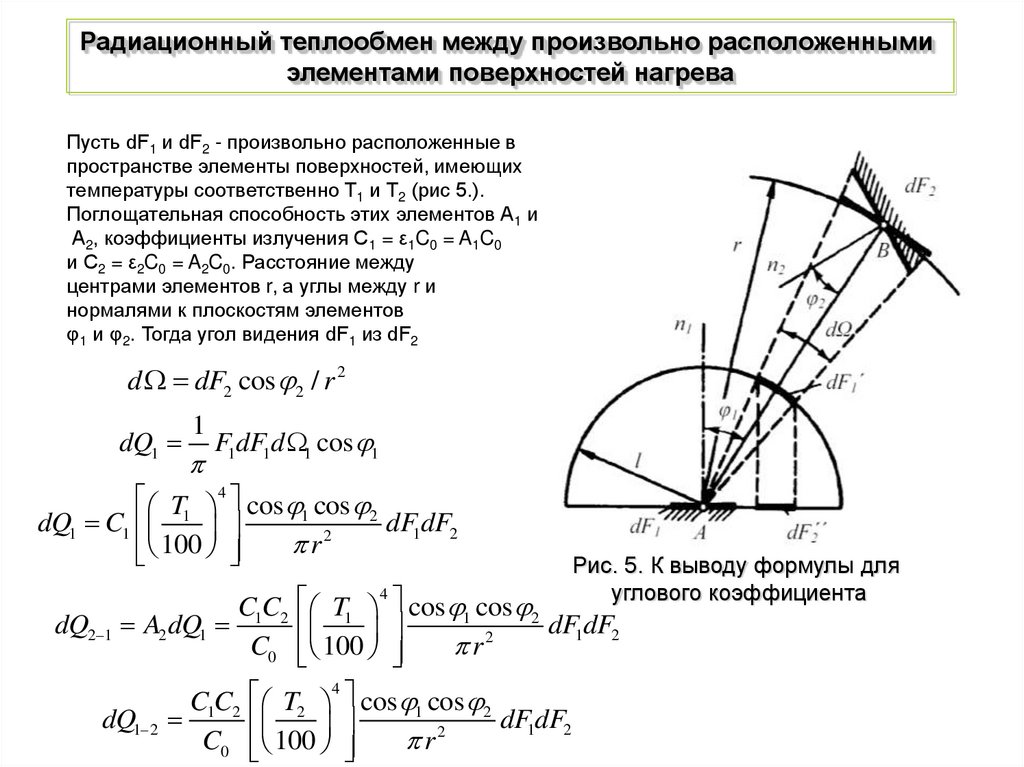
Пусть dF1 и dF2 - произвольно расположенные в
пространстве элементы поверхностей, имеющих
температуры соответственно Т1 и Т2 (рис 5.).
Поглощательная способность этих элементов А1 и
А2, коэффициенты излучения С1 = ε1C0 = A1C0
и С2 = ε2C0 = A2C0. Расстояние между
центрами элементов r, а углы между r и
нормалями к плоскостям элементов
φ1 и φ2. Тогда угол видения dF1 из dF2
d dF2 cos 2 / r 2
dQ1
1
F1dF1d 1 cos 1
T1 4 cos 1 cos 2
dQ1 C1
dF1dF2
2
r
100
CC
dQ2 1 A2 dQ1 1 2
C0
dQ1 2
CC
1 2
C0
Рис. 5. К выводу формулы для
углового коэффициента
T1 4 cos 1 cos 2
dF1dF2
2
r
100
T2 4 cos 1 cos 2
dF1dF2
2
r
100

10.

dQ dQ2 1 dQ1 2
CC
dQ 1 2
C0
4
T1
T2 cos 1 cos 2
dF1dF2
2
r
100 100
dQ Cпр0
4
T1
T2 cos 1 cos 2
dF1dF2
2
r
100 100
где
(8)
Спр0 С1С2 / С0
dQ Cпр0
4
T1
T2
cos 1 cos 2
dF
dF2
1
2
r
100 100 F1
F2
(9)
cos 1 cos 2
F12 dF1
dF2
2
r
F1
F2
Отношение потока излучения от поверхности одного тела на поверхность другого тела к полному
потоку собственного излучения, выходящему со всей поверхности первого тела по всевозможным
направлениям в пределах полусферического телесного угла, называется средним угловым
коэффициентом излучения, или коэффициентом облученности, и обозначается φik.
12 Q12 / Q1
21 Q21 / Q2
(10)

11.

Q C1 T1 /100 F1
4
cos 1 cos 2
T
Q12 C1 1 dF1
dF2
2
r
100 F1
F2
12 F1 21F2
Для n поверхностей
ik Fi ki Fk
Где i = 1, 2, 3,…, n;
k = 1, 2, 3,…, n
Когда поверхность тела имеет вогнутость, возможно самооблучение (i = k), тогда
ii Qii / Qi
Если тела образуют замкнутую систему
n
k 1
ik
1
Qik ik Qi

12.

Интегральные характеристики излучения и
поглощения полупрозрачного объема
Для расчета полного (интегрального, т.е. по всему спектру) потока излучения введем понятие
полной, или интегральной степени черноты газа ε, которая определяется как отношение полного
потока излучения газа Ег к полному потоку излучения абсолютно черного тела при температуре,
равной температуре газа:
E
г г
E0
Eпогл
Aг
Eпад
E 1 e
E d
г
0
lэф
E
пад
(11)
0T 4
пад
0
0
d A
г
d
0
0
E пад d
(12)
E
пад
d
0
Лишь в условиях термодинамического равновесия между падающим излучением и поглощающей
средой, когда падающее излучение является абсолютно черным, выражения (11) и (12) совпадают,
что означает справедливость в этих условиях закона Кирхгофа для поглощающей и излучающей
сред: εг = Аг.
Eг г 0T 4

13.

Радиационный теплообмен в газах
Типы полупрозрачных сред:
1.
газовые среды;
2. запыленные среды;
3.
светящееся пламя
Характеристики излучения газов
E
2. Угловая плотность объемного излучения
j
dQ
dVd d s
3. Спектральная плотность объемного излучения
c, 4 j
T=const
4. Закон Бугера
dI , s
d
d
I , s
1. Спектральная интенсивность изл.
S
dQ
K
5. Спектральная оптическая длина луча
I M, s2
I M, s1
l
exp K ds
0
K const, l K l ,
l
l K ds
0
I M, s2 I M, s1 e K l I M, s1 e l
6. Спектральная плотность
объемного поглощения излучения
d s
S
dFS
K ds
I , s
dQ
dFs d s d
пог ,
4
I
0
,s
d s

14.

Обычно в веществе количество атомов в основном состоянии гораздо больше, чем атомов
возбужденных. Поэтому световая волна, проходя по веществу, расходует свою энергию на
возбуждение атомов. Интенсивность излучения при этом падает, подчиняясь закону Бугера:
Il = I0e–kl
где I0 – исходная интенсивность, Il – интенсивность излучения, прошедшего расстояние l в
веществе с коэффициентом поглощения k. Из уравнения видно, что среда поглощает свет
очень сильно – по экспоненциальному закону.
Вещество, в котором возбужденных атомов гораздо больше, чем атомов в основном состоянии,
называется активным.
г весьма сильно зависит от температуры, так что
Следует иметь в виду, что величина
плотность излучения, проходящего через границу газового объёма, не пропорциональна
четвёртой степени температуры газа. Так, при прочих равных условиях, плотность излучения
углекислоты пропорционально температуре в степени 3,5, а водяного пара – в степени 3.
Из уравнений (12) видно, что при достаточно большой длине луча lэф спектральные степени
черноты и поглощательная способность газа в отдельных полосах поглощения могут достигнуть
значения единицы, т.е. излучательные свойства слоя газа в этих полосах могут сравняться с
излучательными свойствами абсолютно чёрного тела.
При невысоких давлениях поглощение лучистой энергии в газах подчиняется закону Бэра,
согласно которому количество поглощённой лучистой энергии на длине луча пропорционально
числу поглощающих частиц на этой длине. Вследствие этого коэффициент поглощения и
соответственно степень черноты должны быть пропорциональны длине луча и парциальному
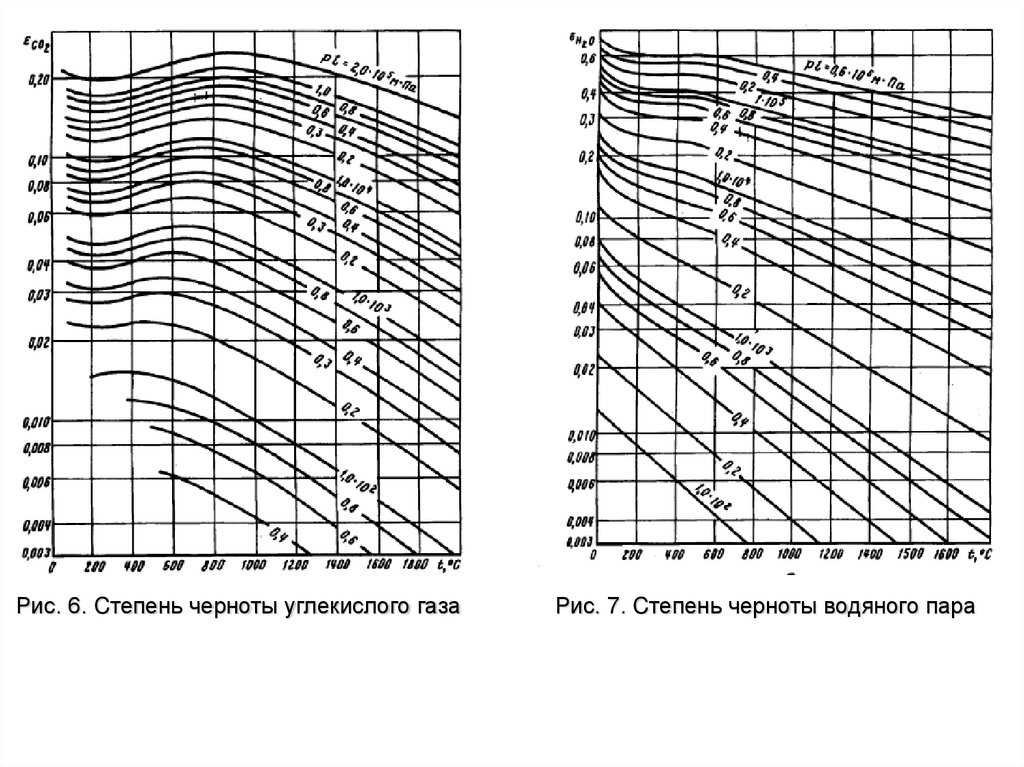
давлению поглощающего (излучающего) газа. Поэтому сведения о степени черноты газов
гприводится
f ( plэф , T )в виде зависимостей
, где p - парциальное давление газа, lэф - эффективная длина луча в газовом
объёме.

15.

Рис. 6. Cтепень черноты углекислого газа
Рис. 7. Cтепень черноты водяного пара

16.

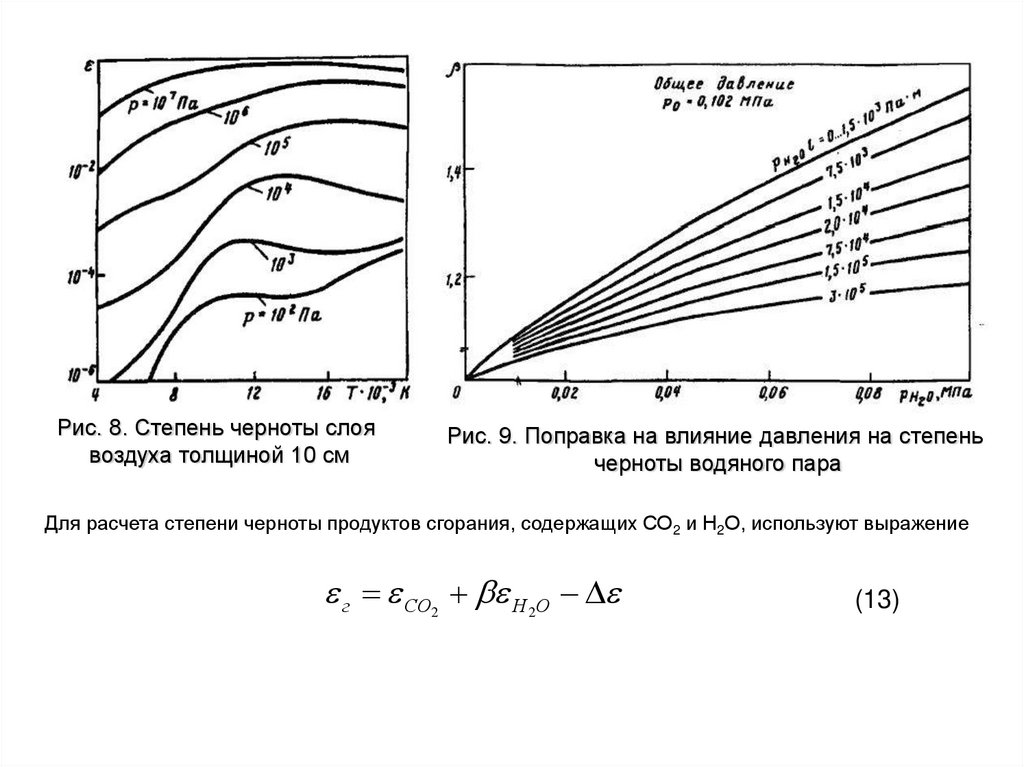
Рис. 8. Степень черноты слоя
воздуха толщиной 10 см
Рис. 9. Поправка на влияние давления на степень
черноты водяного пара
Для расчета степени черноты продуктов сгорания, содержащих СО2 и Н2О, используют выражение
г CO H O
2
2
(13)

17.

Радиационный теплообмен между газом и оболочкой
Радиационный теплообмен между газом и окружающей газ оболочкой может быть представлен как результ
многократных поглощений и отражений стенкой потока, излучаемого газом, и многократных поглощений и
пропусканий газом потока, излучаемого стенкой. Если при этом температура стенки постоянна по всей
поверхности, то лучистый тепловой поток может быть найден по формуле, полученной для расчета
теплообмена между твердым телом и окружающей его оболочкой при малом зазоре между ними:
г ст
q
0 T 4 Tст4
г ст г ст
г
q Eг .эф Eст.эф
(14)
E Г .эф Eг .соб Eст.эф (1 Aг )
Eст.эф Eст.соб Eг.эф (1 Aст )
Рис. 10. Теплообмен между газом
и оболочкой
Aст Eг .соб Aг Eст.соб
q
1 (1 Aст )(1 Aг )
(15)
(16)

18.

4
ст г 0Т Г4 Aг ст 0Т ст
q
1 (1 ст )(1 Aг )
ст
4
0 гТ г4 AгТ ст
1 (1 ст )(1 Aг )
'
ст
ст
1 (1 ст )(1 AГ )
(17)
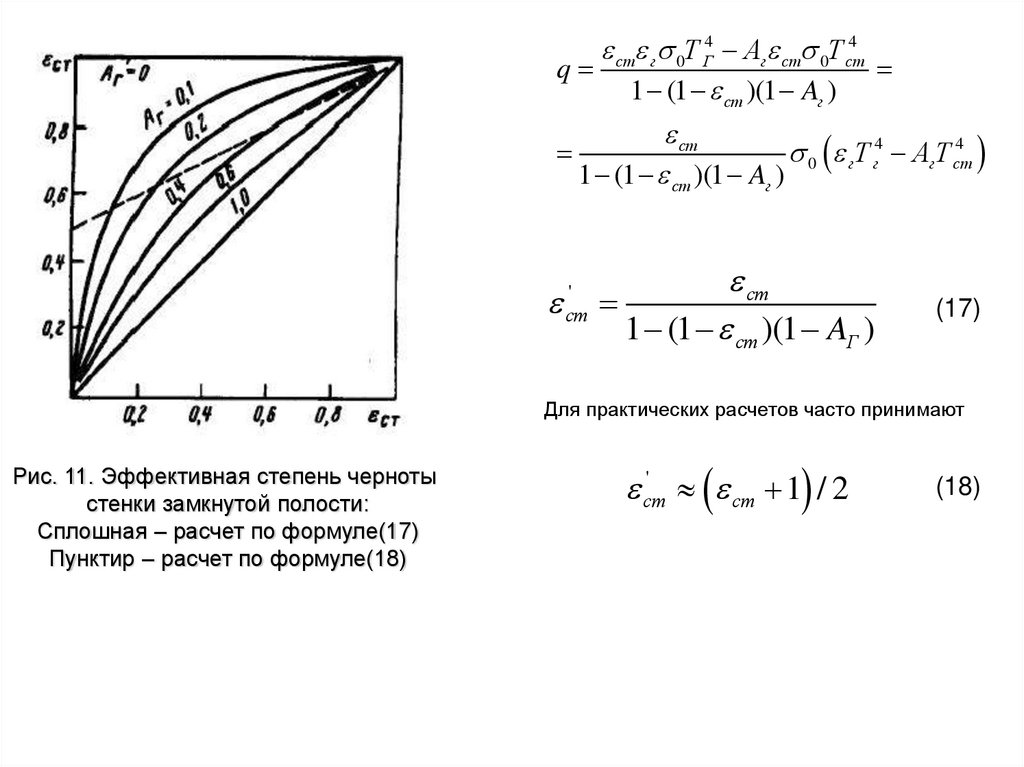
Для практических расчетов часто принимают
Рис. 11. Эффективная степень черноты
стенки замкнутой полости:
Сплошная – расчет по формуле(17)
Пунктир – расчет по формуле(18)
'
ст
ст 1 / 2
(18)

19. Контрольные вопросы

Основные понятия и определения. Белое, зеркальное, серой тело.
Основные законы лучистого теплообмена
Различные случаи теплообмена излучением
Радиационный теплообмен между произвольно расположенными элементами
поверхностей нагрева
Интегральные характеристики излучения и поглощения полупрозрачного
объема
Радиационный теплообмен в газах
Радиационный теплообмен между газом и оболочкой
Закон Стефана-Больцмана
Закон Кирхгофа
Закон Ламберта
Закон Планка
Закон Вина