Similar presentations:
Правильные многогранники
1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если егогранями являются равные правильные многоугольники и в каждой
вершине сходится одинаковое число граней.
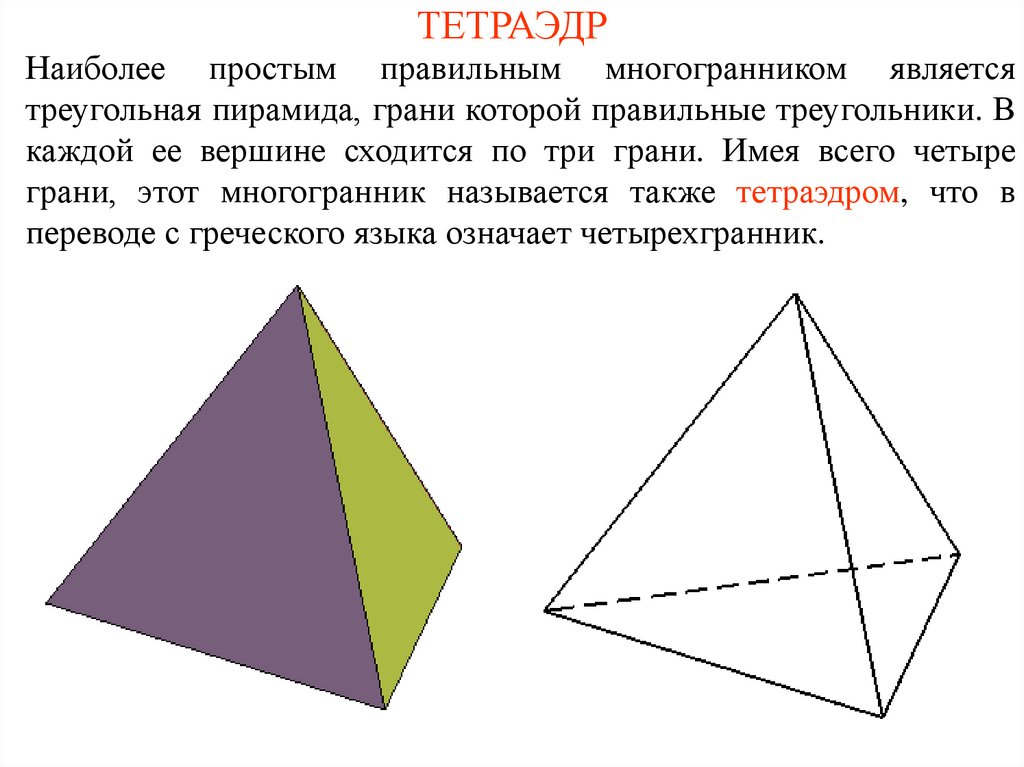
2. ТЕТРАЭДР
Наиболее простым правильным многогранником являетсятреугольная пирамида, грани которой правильные треугольники. В
каждой ее вершине сходится по три грани. Имея всего четыре
грани, этот многогранник называется также тетраэдром, что в
переводе с греческого языка означает четырехгранник.
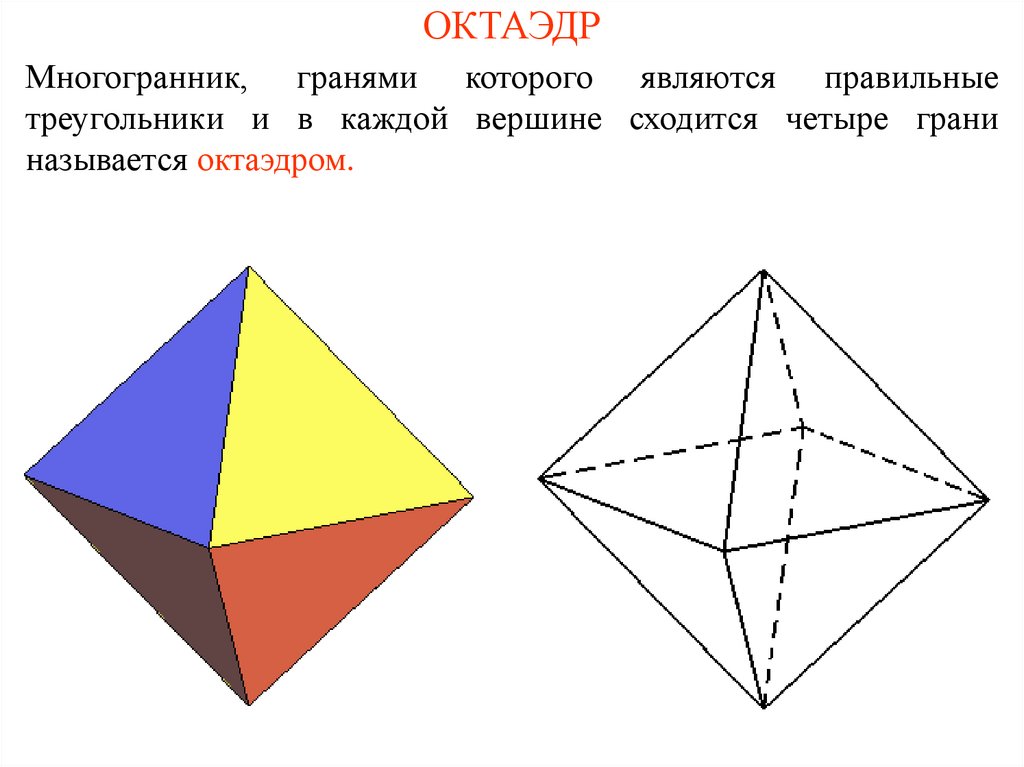
3. ОКТАЭДР
Многогранник, гранями которого являются правильныетреугольники и в каждой вершине сходится четыре грани
называется октаэдром.
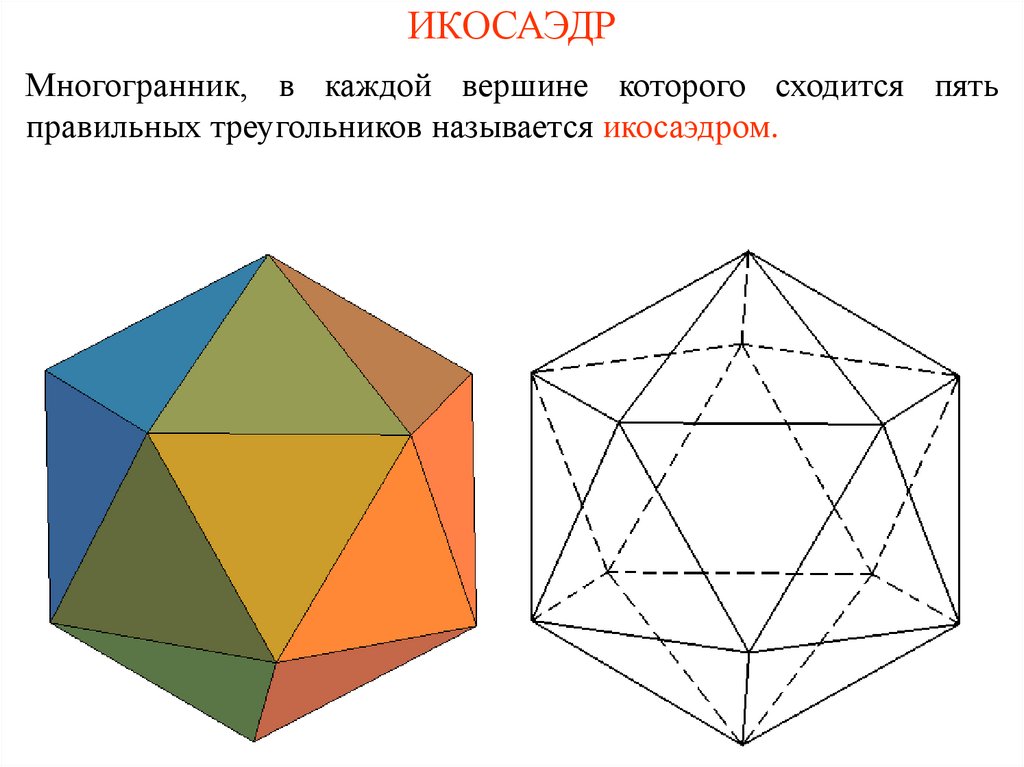
4. ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пятьправильных треугольников называется икосаэдром.
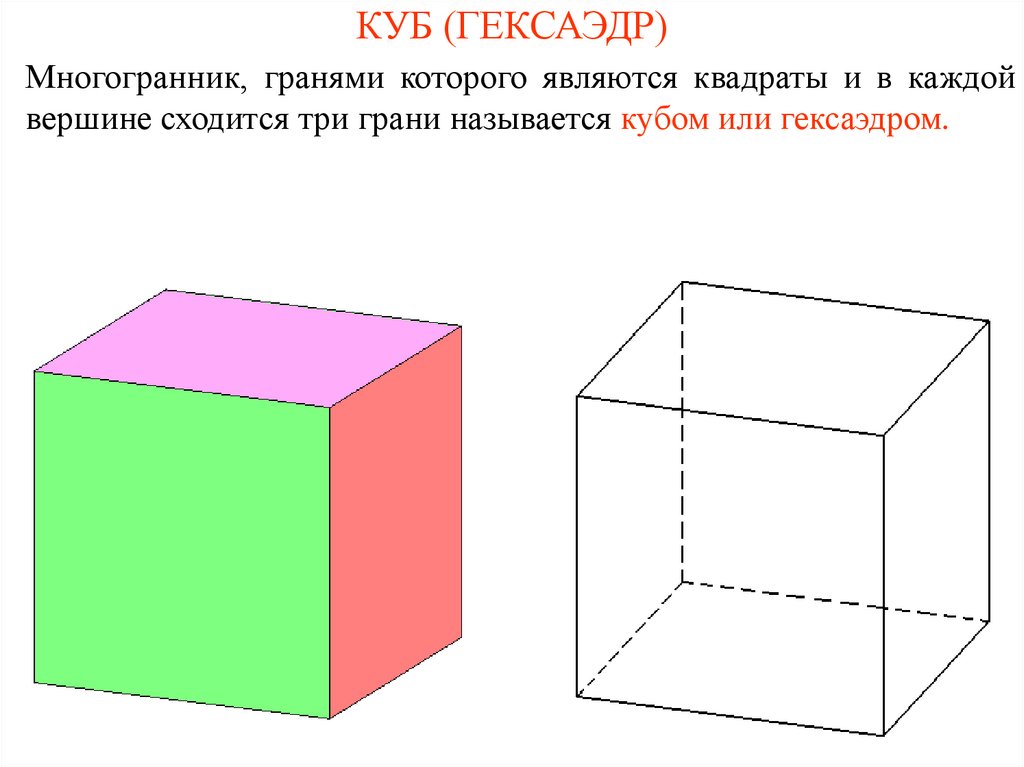
5. КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в каждойвершине сходится три грани называется кубом или гексаэдром.
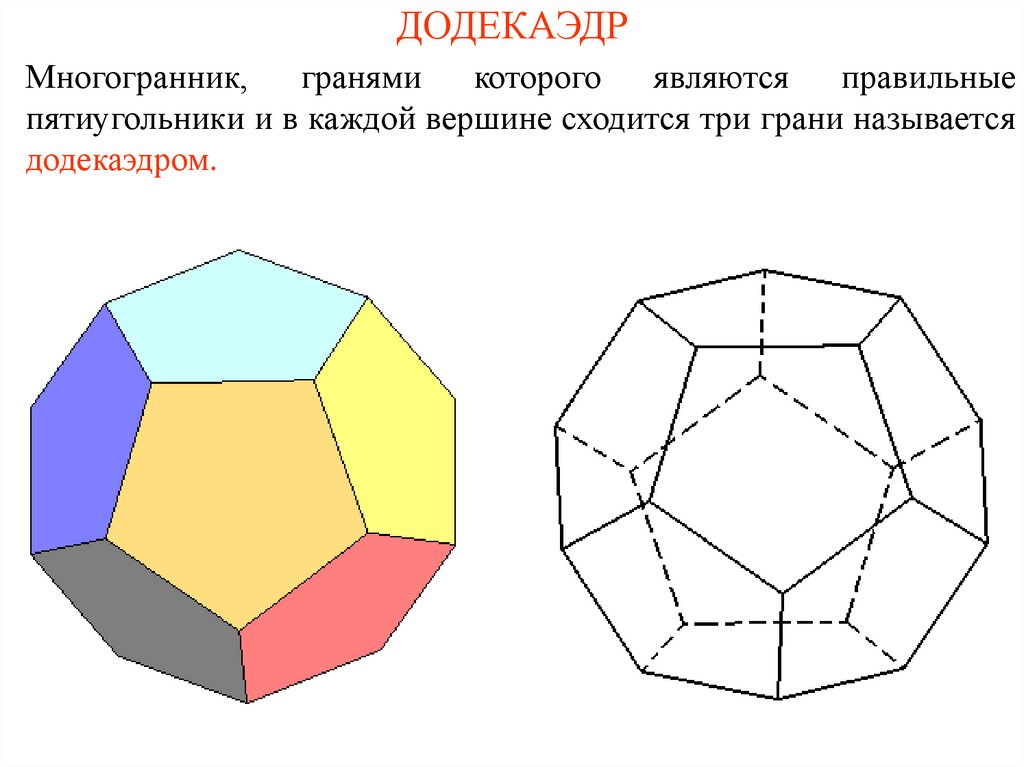
6. ДОДЕКАЭДР
Многогранник,гранями
которого
являются
правильные
пятиугольники и в каждой вершине сходится три грани называется
додекаэдром.
7. Кубок Кеплера
Иоганн Кеплер (1571-1630) в своей работе "Тайна мироздания" в1596 году, используя правильные многогранники, вывел принцип,
которому подчиняются формы и размеры орбит планет Солнечной
системы.
8. Упражнение 1
Представьте многогранник - бипирамиду, сложенную издвух равных тетраэдров совмещением каких-нибудь их
граней. Будет ли он правильным многогранником?
Ответ: Нет.
9. Упражнение 2
Представьте многогранник - бипирамиду, сложенную издвух правильных четырехугольных пирамид, ребра
которых равны 1, совмещением их оснований. Будет ли
он правильным многогранником?
Ответ: Да, октаэдром.
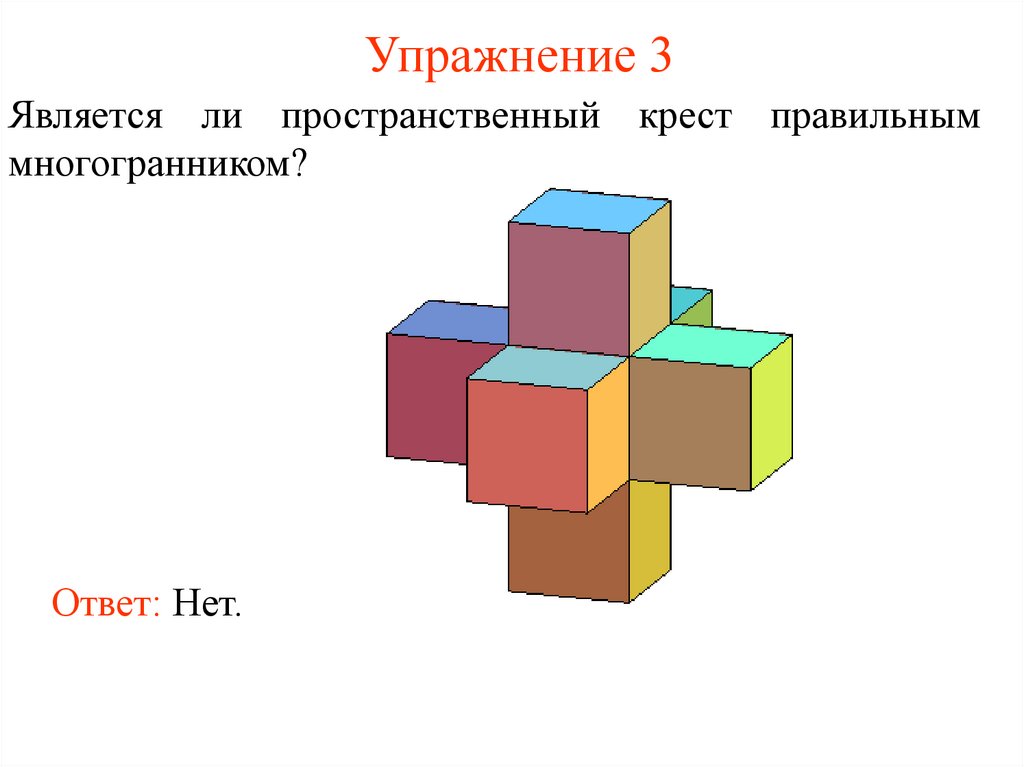
10. Упражнение 3
Является ли пространственный крест правильныммногогранником?
Ответ: Нет.
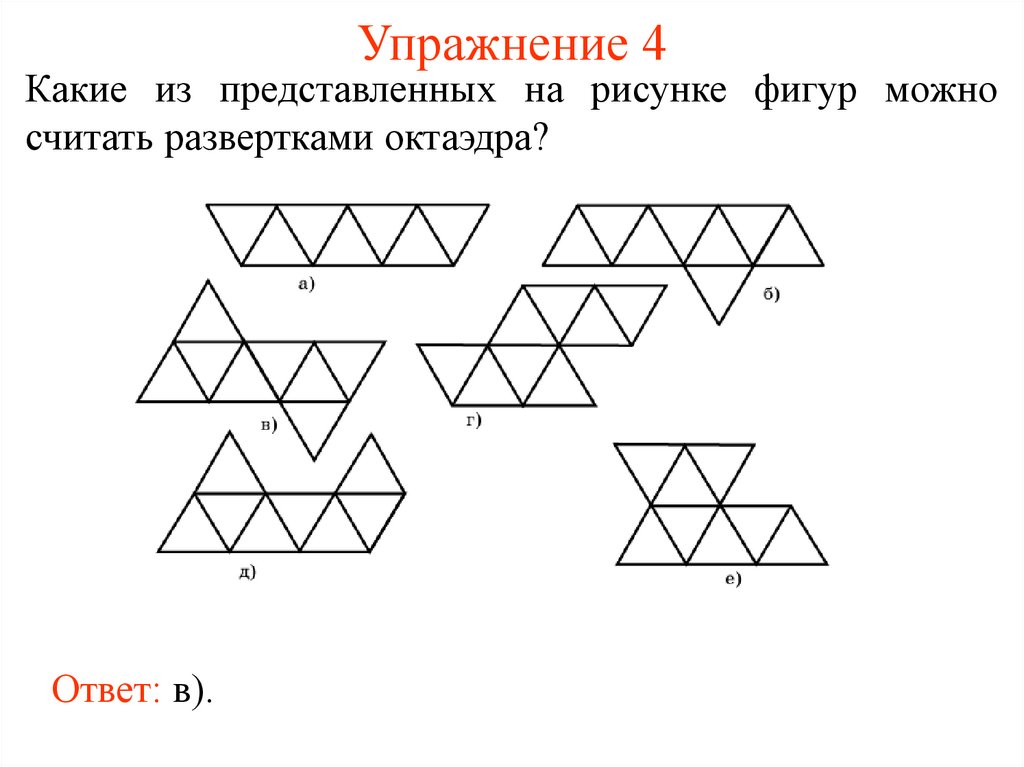
11. Упражнение 4
Какие из представленных на рисунке фигур можносчитать развертками октаэдра?
Ответ: в).
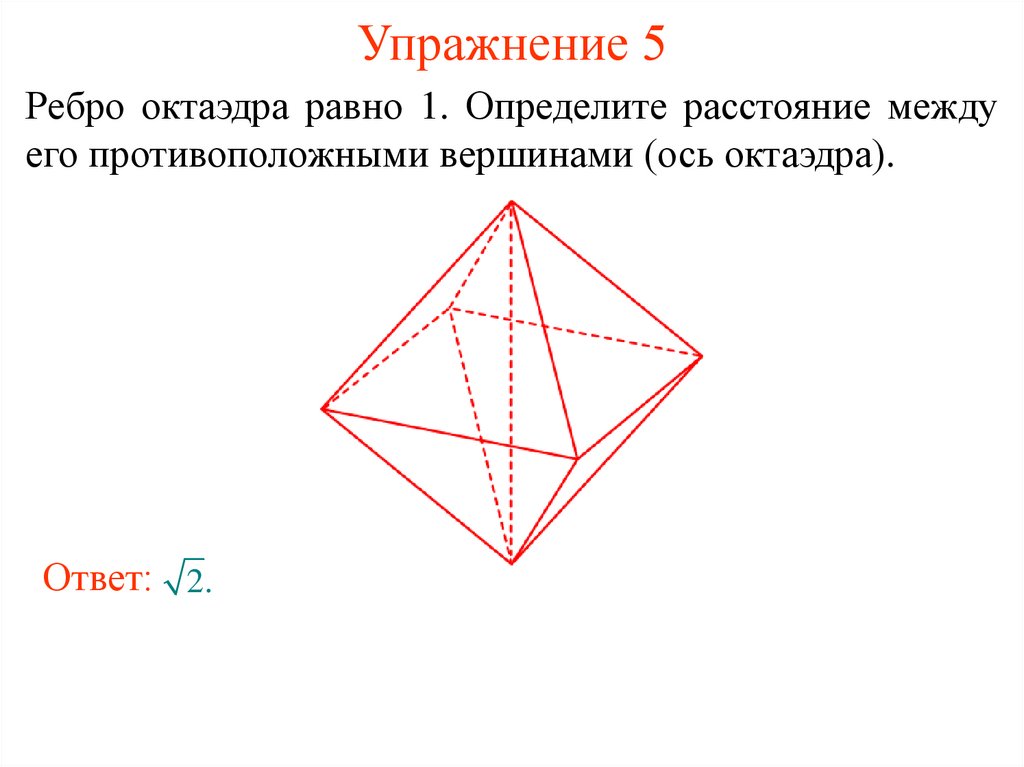
12. Упражнение 5
Ребро октаэдра равно 1. Определите расстояние междуего противоположными вершинами (ось октаэдра).
Ответ: 2.
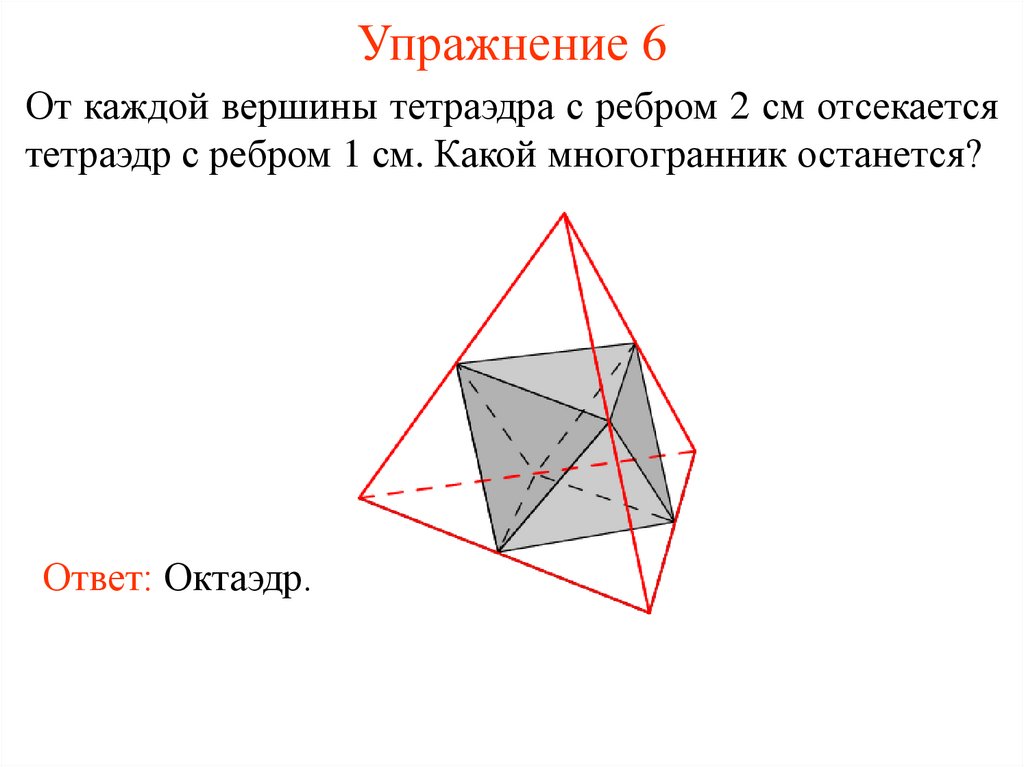
13. Упражнение 6
От каждой вершины тетраэдра с ребром 2 см отсекаетсятетраэдр с ребром 1 см. Какой многогранник останется?
Ответ: Октаэдр.
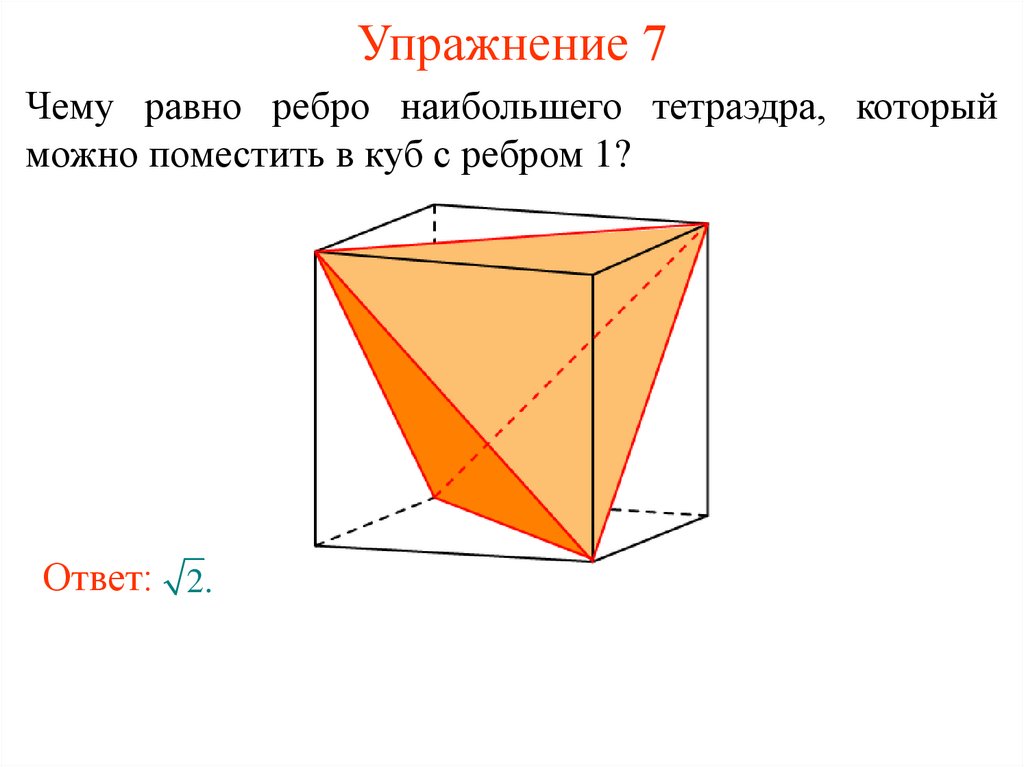
14. Упражнение 7
Чему равно ребро наибольшего тетраэдра, которыйможно поместить в куб с ребром 1?
Ответ: 2.
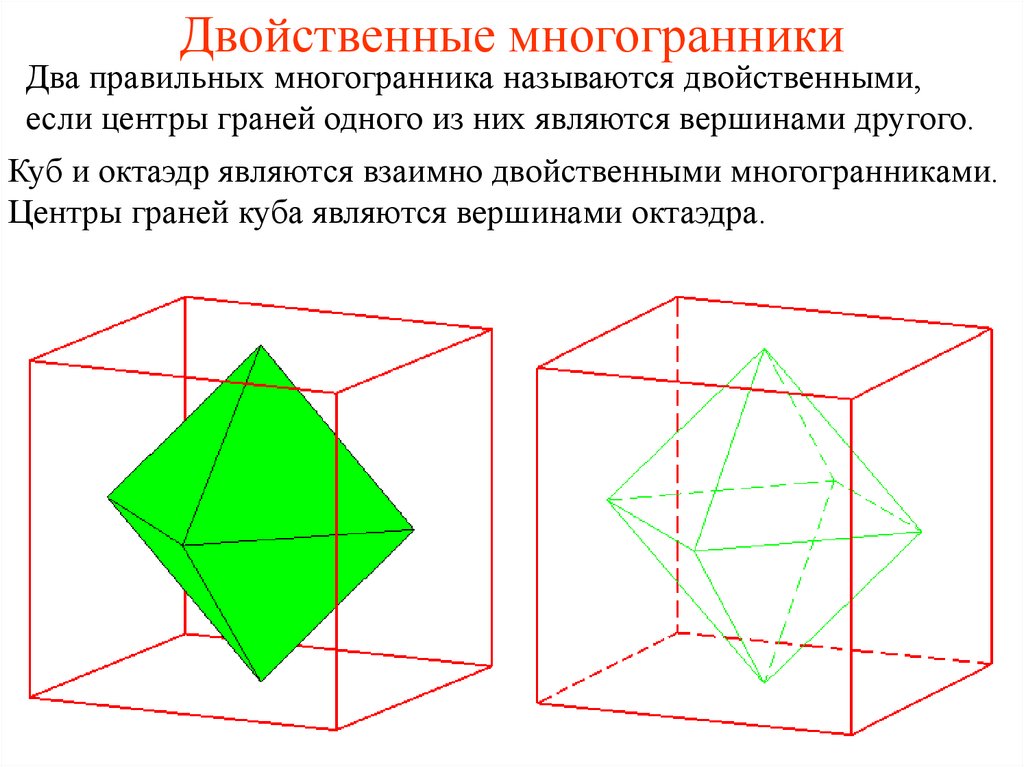
15. Двойственные многогранники
Два правильных многогранника называются двойственными,если центры граней одного из них являются вершинами другого.
Куб и октаэдр являются взаимно двойственными многогранниками.
Центры граней куба являются вершинами октаэдра.
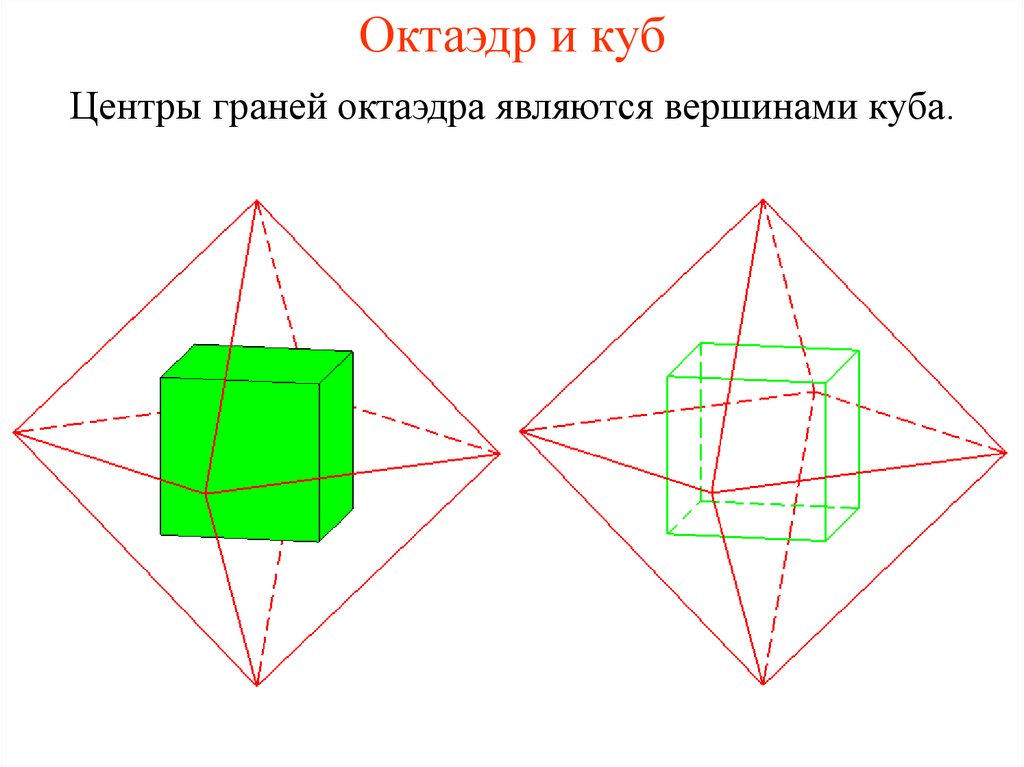
16. Октаэдр и куб
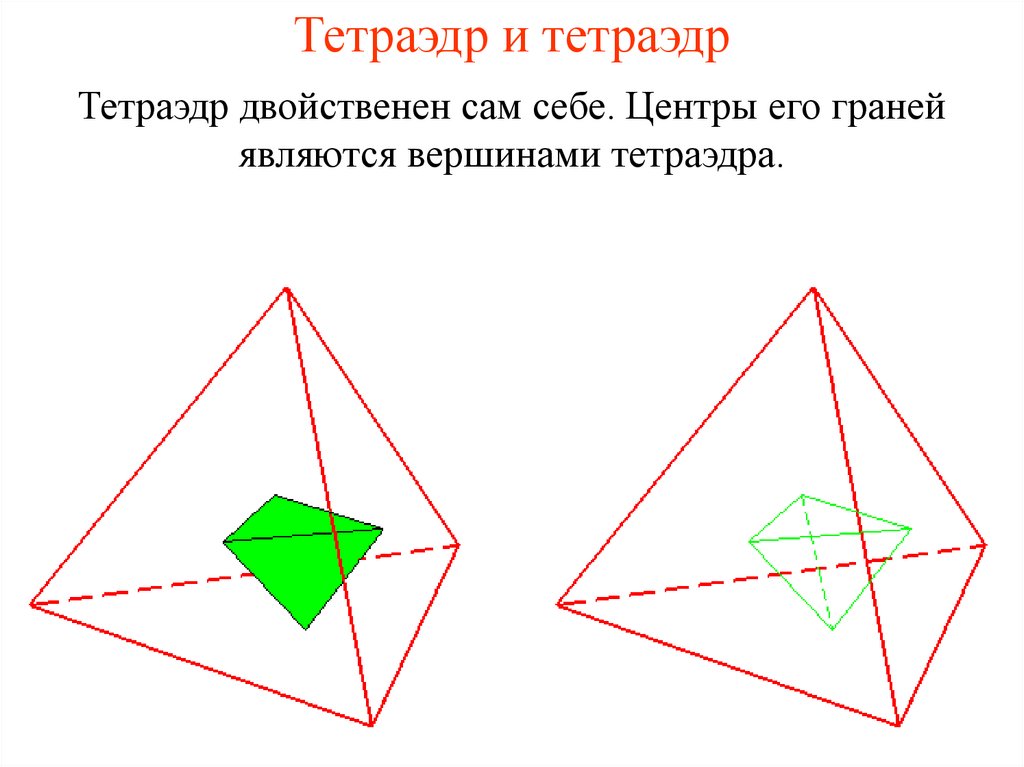
Центры граней октаэдра являются вершинами куба.17. Тетраэдр и тетраэдр
Тетраэдр двойственен сам себе. Центры его гранейявляются вершинами тетраэдра.
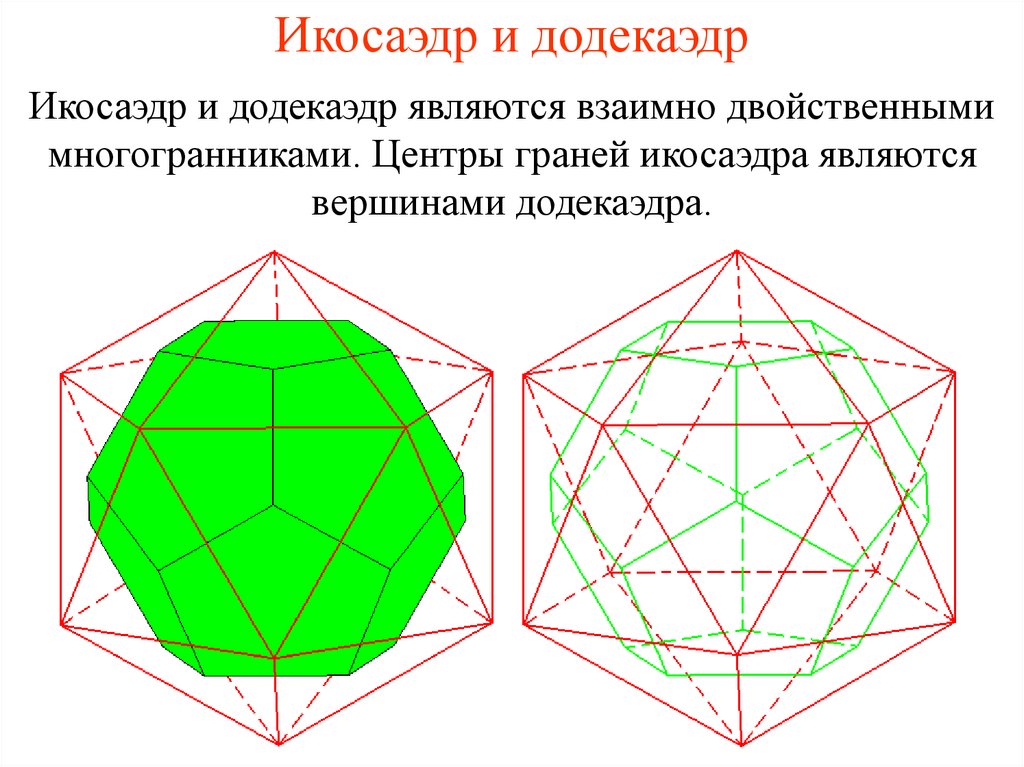
18. Икосаэдр и додекаэдр
Икосаэдр и додекаэдр являются взаимно двойственнымимногогранниками. Центры граней икосаэдра являются
вершинами додекаэдра.
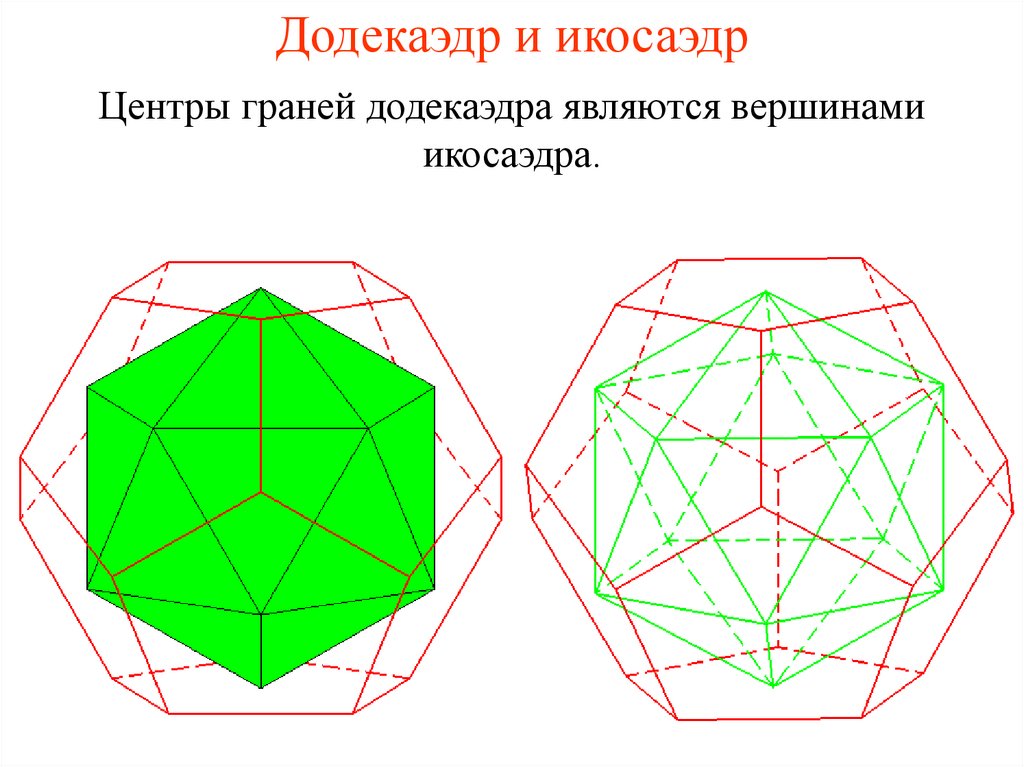
19. Додекаэдр и икосаэдр
Центры граней додекаэдра являются вершинамиикосаэдра.
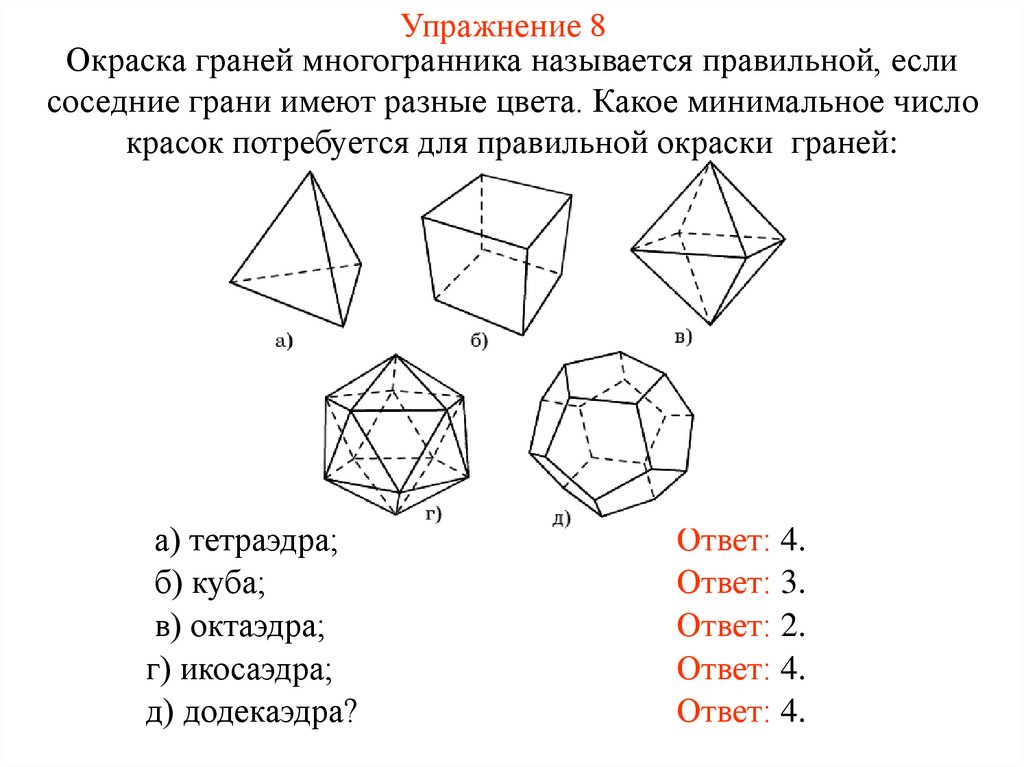
20. Упражнение 8
Окраска граней многогранника называется правильной, еслисоседние грани имеют разные цвета. Какое минимальное число
красок потребуется для правильной окраски граней:
а) тетраэдра;
б) куба;
в) октаэдра;
г) икосаэдра;
д) додекаэдра?
Ответ: 4.
Ответ: 3.
Ответ: 2.
Ответ: 4.
Ответ: 4.




 mathematics
mathematics








