Кривые постоянной ширины

1. Кривые постоянной ширины

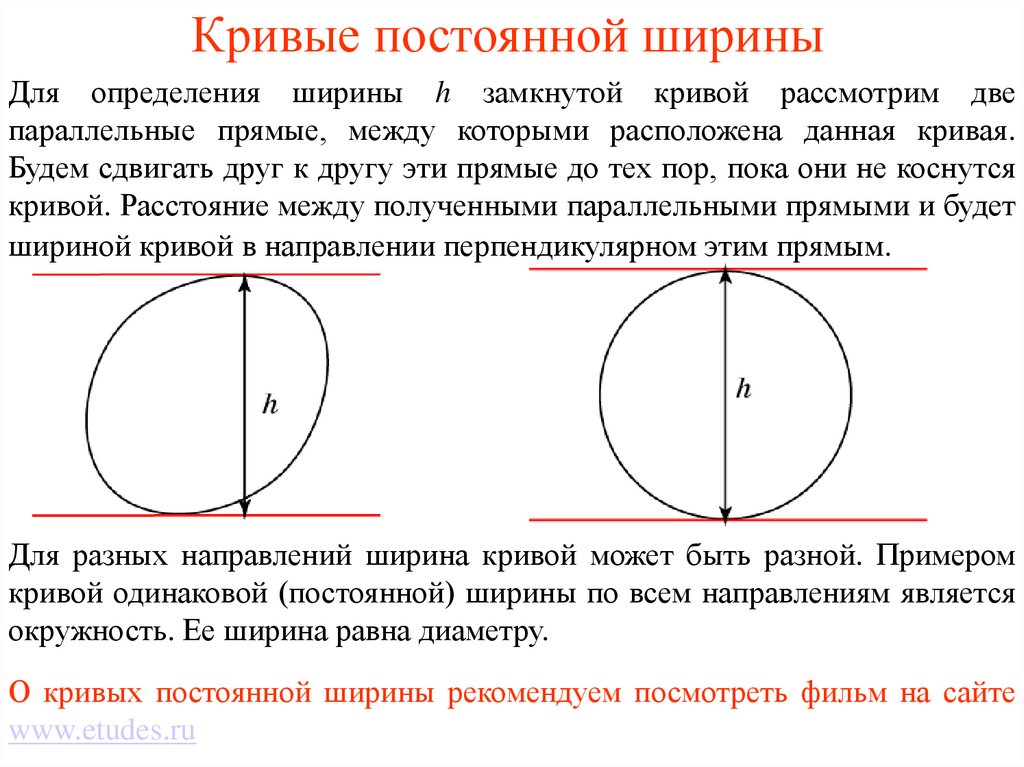
Для определения ширины h замкнутой кривой рассмотрим две
параллельные прямые, между которыми расположена данная кривая.
Будем сдвигать друг к другу эти прямые до тех пор, пока они не коснутся
кривой. Расстояние между полученными параллельными прямыми и будет
шириной кривой в направлении перпендикулярном этим прямым.
Для разных направлений ширина кривой может быть разной. Примером
кривой одинаковой (постоянной) ширины по всем направлениям является
окружность. Ее ширина равна диаметру.
О кривых постоянной ширины рекомендуем посмотреть фильм на сайте
www.etudes.ru

2. Треугольник Рело

Бывают ли кривые, отличные от окружности и имеющие постоянную
ширину?
Оказывается, бывают. Примером такой кривой является кривая,
придуманная французским ученым Ф. Рело (1829 – 1905), называемая
«треугольник Рело».
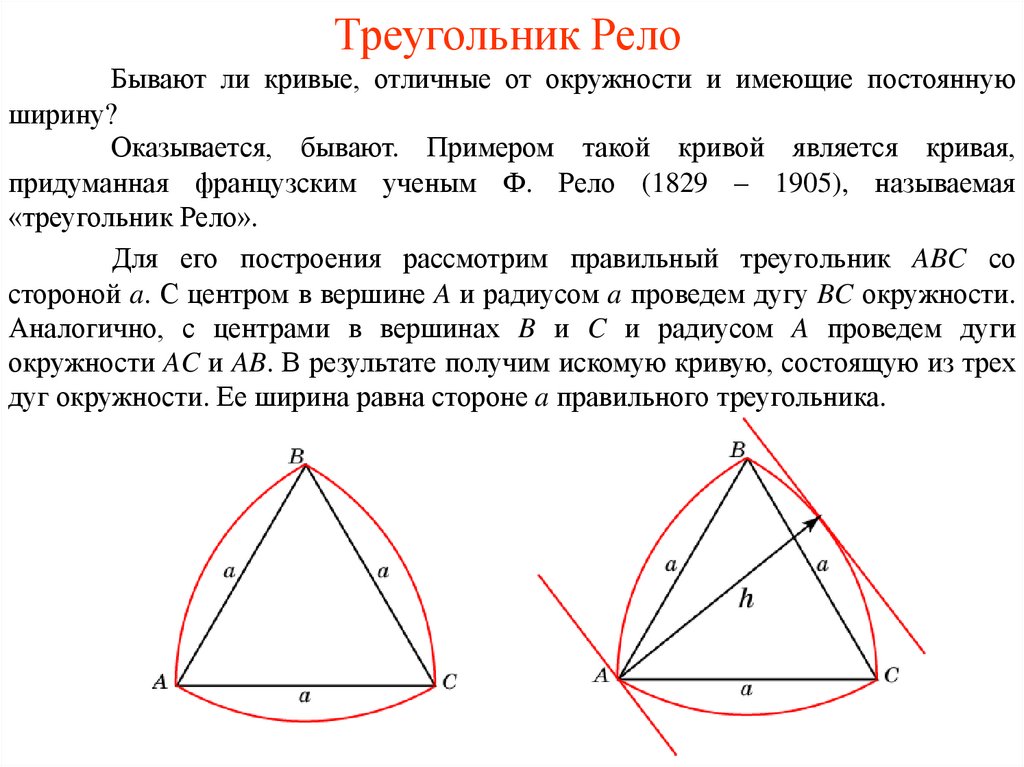
Для его построения рассмотрим правильный треугольник ABC со
стороной a. С центром в вершине A и радиусом a проведем дугу BC окружности.
Аналогично, с центрами в вершинах B и C и радиусом A проведем дуги
окружности AC и AB. В результате получим искомую кривую, состоящую из трех
дуг окружности. Ее ширина равна стороне a правильного треугольника.

3. Упражнение 1

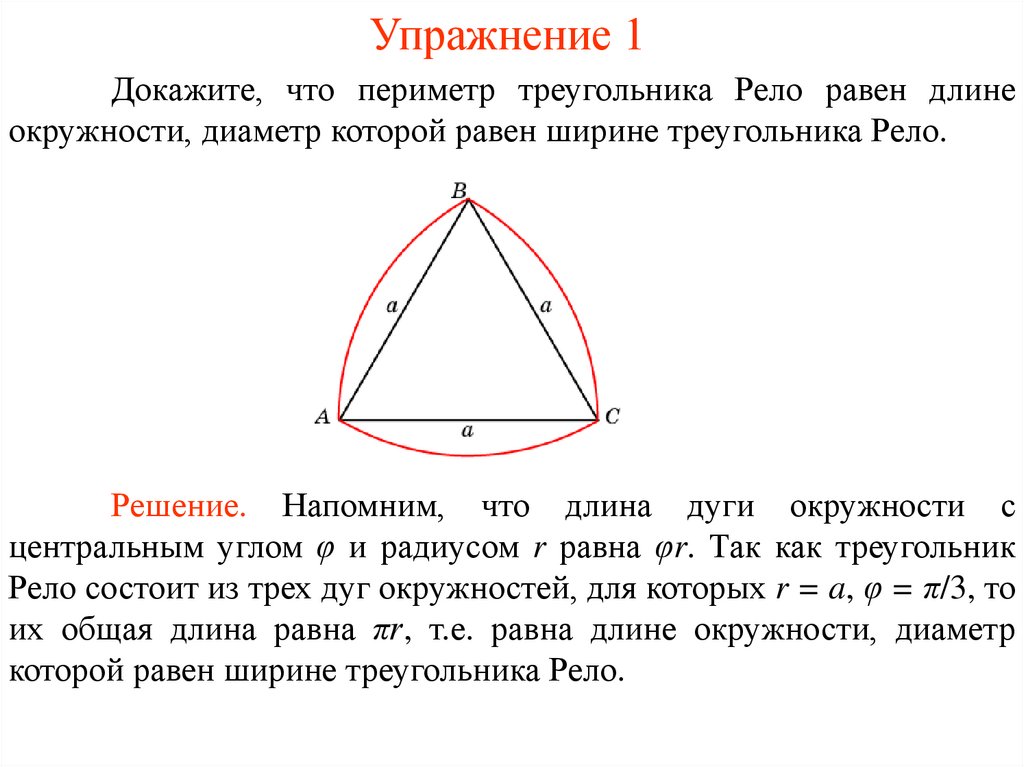
Докажите, что периметр треугольника Рело равен длине
окружности, диаметр которой равен ширине треугольника Рело.
Решение. Напомним, что длина дуги окружности с
центральным углом φ и радиусом r равна φr. Так как треугольник
Рело состоит из трех дуг окружностей, для которых r = a, φ = π/3, то
их общая длина равна πr, т.е. равна длине окружности, диаметр
которой равен ширине треугольника Рело.

4. Упражнение 2

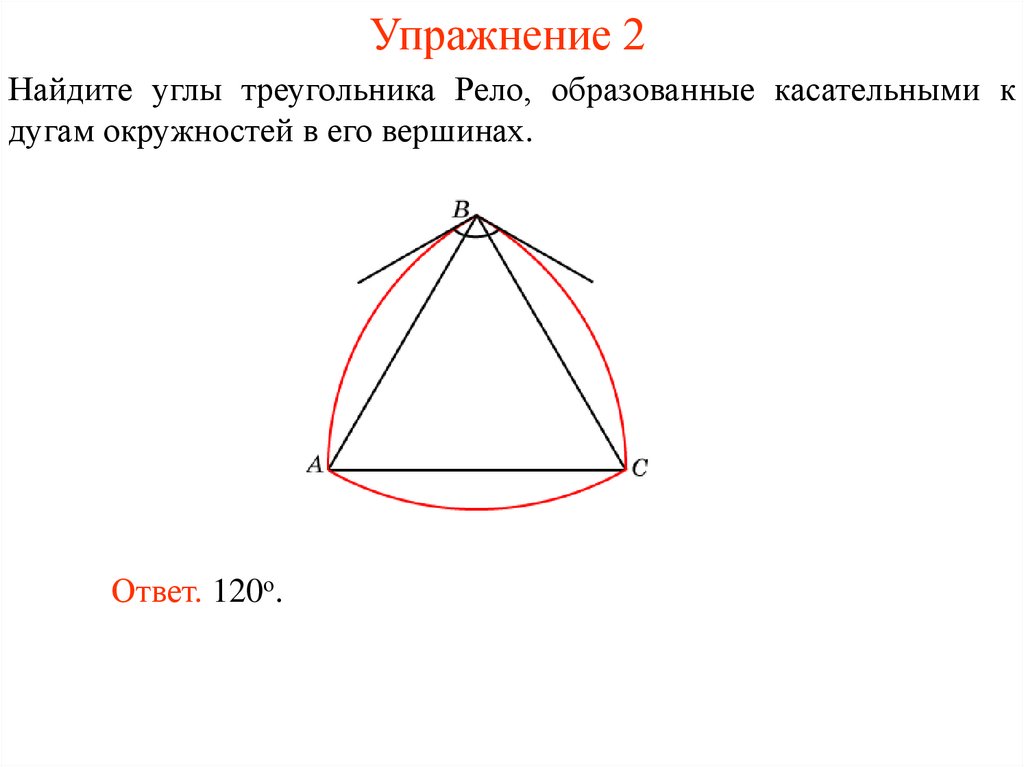
Найдите углы треугольника Рело, образованные касательными к
дугам окружностей в его вершинах.
Ответ. 120о.

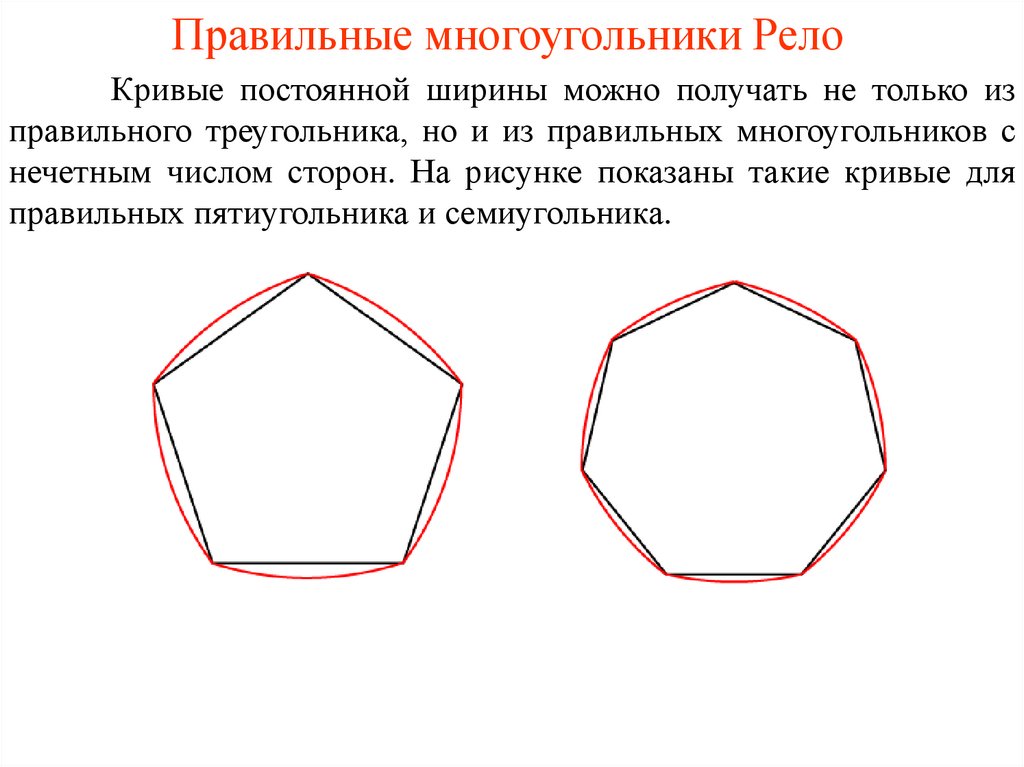
5. Правильные многоугольники Рело

Кривые постоянной ширины можно получать не только из
правильного треугольника, но и из правильных многоугольников с
нечетным числом сторон. На рисунке показаны такие кривые для
правильных пятиугольника и семиугольника.

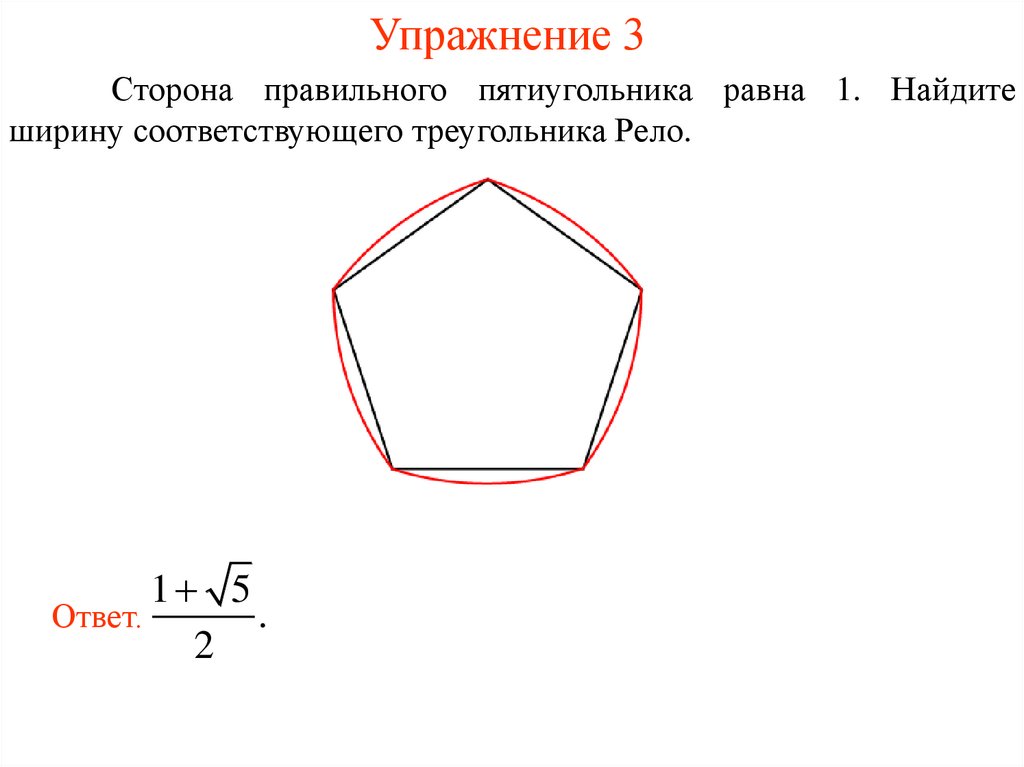
6. Упражнение 3

Сторона правильного пятиугольника равна 1. Найдите
ширину соответствующего треугольника Рело.
1 5
.
Ответ.
2

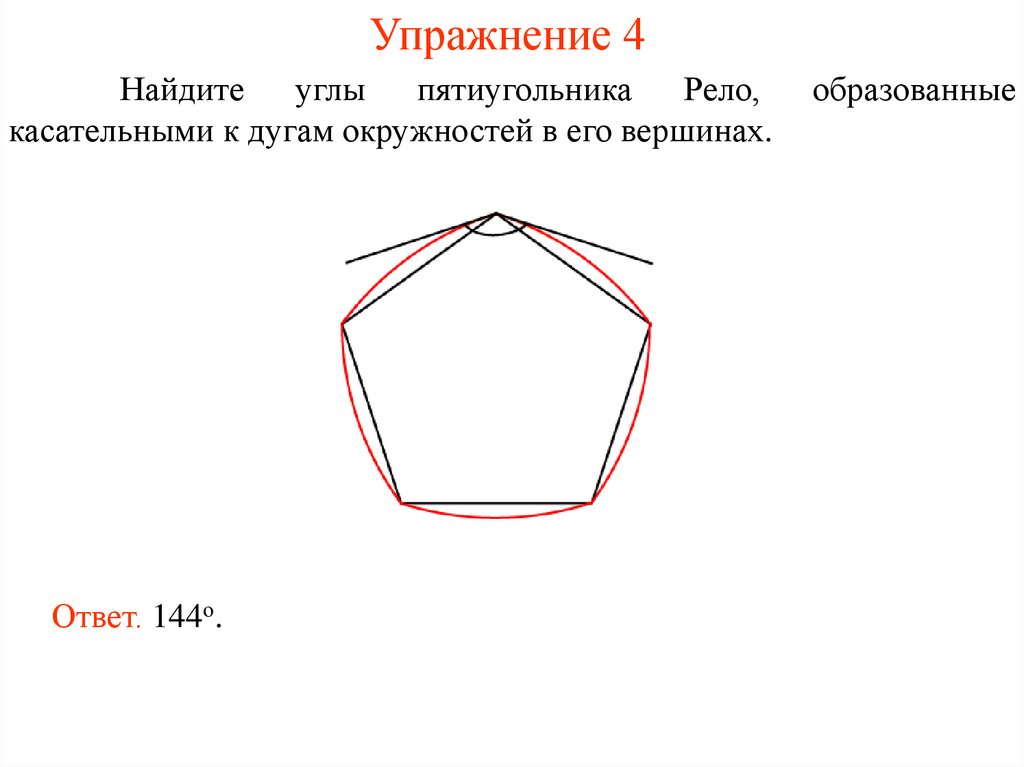
7. Упражнение 4

Найдите
углы
пятиугольника
Рело,
касательными к дугам окружностей в его вершинах.
Ответ. 144о.
образованные

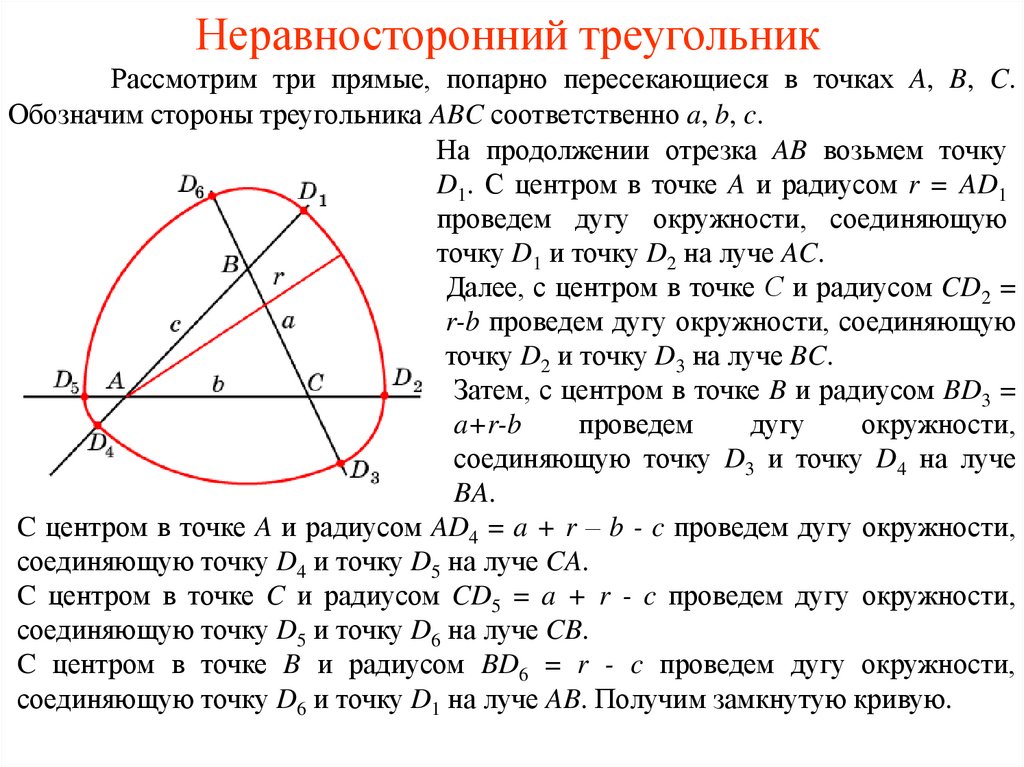
8. Неравносторонний треугольник

Рассмотрим три прямые, попарно пересекающиеся в точках A, B, C.
Обозначим стороны треугольника ABC соответственно a, b, c.
На продолжении отрезка AB возьмем точку
D1. С центром в точке A и радиусом r = AD1
проведем дугу окружности, соединяющую
точку D1 и точку D2 на луче AC.
Далее, с центром в точке С и радиусом CD2 =
r-b проведем дугу окружности, соединяющую
точку D2 и точку D3 на луче BC.
Затем, с центром в точке B и радиусом BD3 =
a+r-b
проведем
дугу
окружности,
соединяющую точку D3 и точку D4 на луче
BA.
C центром в точке A и радиусом AD4 = a + r – b - c проведем дугу окружности,
соединяющую точку D4 и точку D5 на луче CA.
C центром в точке C и радиусом CD5 = a + r - c проведем дугу окружности,
соединяющую точку D5 и точку D6 на луче CB.
C центром в точке B и радиусом BD6 = r - c проведем дугу окружности,
соединяющую точку D6 и точку D1 на луче AB. Получим замкнутую кривую.

9. Упражнение 5

Докажите, что полученная кривая имеет
ширину. Найдите ее выражение через a, b, c и r.
постоянную
Решение. Через точку E1 на дуге D1D2 и
точку A проведем прямую. Ее точку
пересечения с дугой D4D5 обозначим E4.
Касательные к кривой в точках E1, E4 будут
перпендикулярны
отрезку
E1E4.
Следовательно, длина этого отрезка будет
шириной кривой h в направлении прямой
E1E4, h = r + a + r – b - c = 2r + a – b – c.
Ясно, что это значение не зависит от
выбора точки E1 на дуге D1D2.
Рассмотрим теперь точку E2 на дуге D2D3. Через нее и точку С проведем прямую.
Ее точку пересечения с дугой D5D6 обозначим E5. Касательные к кривой в точках
E2, E5 будут перпендикулярны отрезку E2E5. Следовательно, длина этого отрезка
будет шириной кривой в направлении прямой E2E5. Она равна r – b + a + r - c = 2r
+ a – b – c = h. Ясно, что это значение не зависит от выбора точки E2 на дуге
D2D3.
Аналогичным образом показывается, что для точек E3 дуги D3D4 ширина кривой
также будет равна 2r + a – b – c = h.

10. Упражнение 6

Докажите, что длина полученной кривой равна длине окружности
с диаметром, равным ширине h кривой.
Решение. Напомним, что длина l дуги окружности радиуса R и центральным
углом φ выражается формулой l = φR.
Пусть углы треугольника ABC равны соответственно α, β, γ. Тогда длина дуги
D1D2 αr, длина дуги D4D5 равна α(a + r – b – c). Их сумма равна αh.
Аналогично, сумма длин дуг D2D3 и D5D6 равна γh, сумма длин дуг D3D4 и D6D1
равна βh.
Таким образом, длина всей кривой равна αh + βh + γh = (α + β + γ)h = πh, т.е.
равна длине окружности с диаметром h.

11. Невыпуклый четырехугольник

Рассмотрим четыре прямые, попарно пересекающиеся в точках A, B, C,
D. Обозначим стороны четырехугольника ABCD соответственно a, b, c, d.
На продолжении отрезка AB возьмем
точку E1. С центром в точке A и радиусом r =
AE1 проведем дугу окружности, соединяющую
точку E1 и точку E2 на луче AD.
Проведите дальнейшее построение
кривой постоянной ширины самостоятельно,
найдите ее ширину. Докажите, что ее длина
равна длине окружности с диаметром, равным
ширине h кривой.
Ответ. Искомая кривая изображена на рисунке, где E2E3 – дуга
окружности с центром D и радиусом r – d, E3E4 – дуга окружности с центром C и
радиусом c + r – d, E4E5 – дуга окружности с центром B и радиусом b + c + r – d,
E5E6 – дуга окружности с центром A и радиусом b + c + r – d – a, E6E7 – дуга
окружности с центром D и радиусом b + c + r – a, E7E8 – дуга окружности с
центром C и радиусом b + r – a, E8E1 – дуга окружности с центром B и радиусом
r – a. Ширина h кривой равна 2r + b + c – a – d.