Similar presentations:
Тупики. Задачи операционной системы
1. Тупики
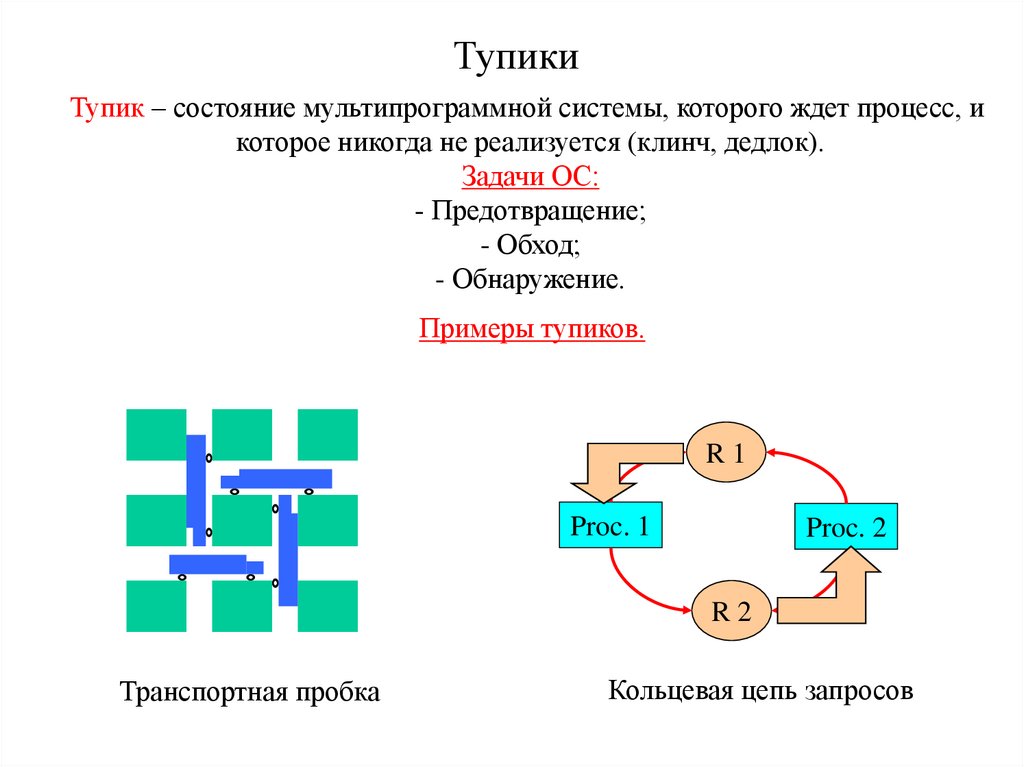
Тупик – состояние мультипрограммной системы, которого ждет процесс, икоторое никогда не реализуется (клинч, дедлок).
Задачи ОС:
- Предотвращение;
- Обход;
- Обнаружение.
Примеры тупиков.
R1
Proc. 1
Proc. 2
R2
Транспортная пробка
Кольцевая цепь запросов
2. Бесконечное ожидание – состояние системы, которого ждет процесс, является возможным, но оно откладывается на неопределенное
время.Например, из-за приоритета.
Ресурсы бывают:
- перераспределяемые (процессор, память);
- монопольные (НМЛ);
- реентерабельные (неизменный код);
- последовательного использования.
Условия возникновения тупиков (необходимые):
1. Монопольное управление выделенными ресурсами (взаимоисключение);
2. Удержание ресурсов на время ожидания следующего;
3. Ресурсы у процесса нельзя отобрать, отдает их сам (неперераспределение);
4. Существование кольцевой цепи запросов.
3. Предотвращение тупиков. Принципы Хавендера.
Хавендер показал, что для предотвращения тупика необходимо нарушитьодно из необходимых условий его возникновения.
Принципы Хавендера:
Процесс запрашивает все нужные ресурсы сразу. До выделения – ждет.
Если процессу не выделяется очередной ресурс, он должен отдать уже
выделенные.
Вводим линейную упорядоченность на типы ресурсов. Процесс может
запросить ресурсы только в порядке увеличения номера ресурса.
Условие монопольного управления Хавендер не нарушает.
4.
Процесс запрашивает все нужные ресурсы сразу. До выделения – ждет.Нарушается условие возникновения тупиков:
2 .Удержание ресурсов на время ожидания следующего;
Плюс: простота реализации.
Минусы:
- Как определить набор всех необходимых процессу ресурсов?
- Простой свободных ресурсов.
- Накапливание ресурсов приводит к высоким издержкам.
Если процессу не выделяется очередной ресурс, он должен отдать уже
выделенные.
Нарушается условие возникновения тупиков:
3. Ресурсы у процесса нельзя отобрать, отдает их сам (неперераспределение);
Плюс: ???.
Минусы:
- Как сохранить промежуточные результаты работы процесса?
- Возможность бесконечного откладывания (дефицитный ресурс).
5.
Вводим линейную упорядоченность на типы ресурсов. Процесс можетзапросить ресурсы только в порядке увеличения номера ресурса.
Нарушается условие возникновения тупиков:
4. Существование кольцевой цепи запросов.
Плюс: кажущаяся простота реализации.
Минусы:
- Сложно вводить в систему новые ресурсы (ОС).
- Кто знает «правильную» последовательность ресурсов?
- Трансляторы тоже должны знать номера ресурсов, а это сложно и
снижает мобильность систем.
Вывод – принципы Хавендера носят скорее теоретический характер.
На практике они используются как вспомогательные элементы стратегий.
6.
Обход тупиков. Алгоритм банкира.Банкир – выдает ссуды (кредиты) тем, кто может их возвратить.
Дейкстра предложил алгоритм обхода тупиков, если все условия их
возникновения не нарушены.
Алгоритм банкира – ресурсы процессу можно выдавать только в том
случае, если состояние системы останется надежным.
Надежное состояние – ОС гарантирует всем процессам завершение в
конечное время.
Введем следующие обозначения:
M(i) – максимальная потребность i-го процесса в ресурсе;
L(i) – текущая величина ресурса, выделенного i-му процессу;
С(i) – текущая потребность в ресурсе, C(i)=M(i)-L(i);
Т – суммарный ресурс, имеющийся в системе;
а – остаточный ресурс, а=Т- L(i);
7.
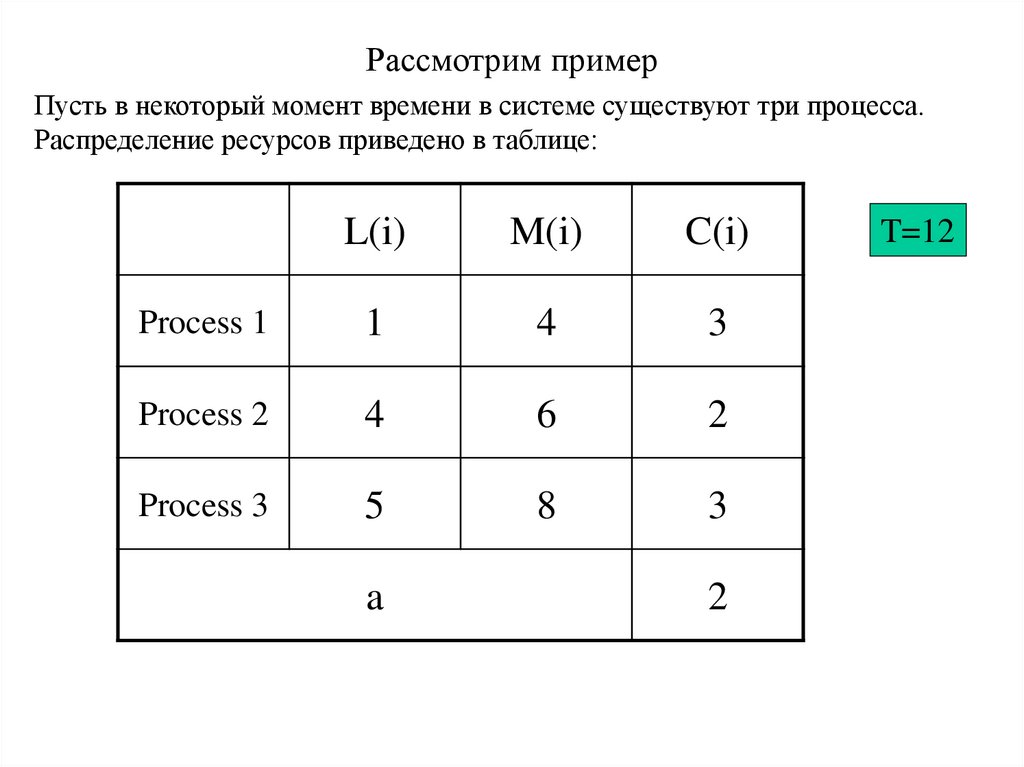
Рассмотрим примерПусть в некоторый момент времени в системе существуют три процесса.
Распределение ресурсов приведено в таблице:
L(i)
M(i)
C(i)
Process 1
1
4
3
Process 2
4
6
2
Process 3
5
8
3
a
2
T=12
8.
Решение примераБудем выделять остаточный ресурс процессам и оценивать состояние системы.
1. Lnew(1) = L(1) + a =1+2=3
C(1)=M(1)-Lnew(1)=4 - 3 =1>0
C(2)=2>0; C(3)=3>0
Все C(i)>0, состояние системы ненадежное.
2. Lnew(3) = L(3) + a =5+2=7
C(3)=M(3)-Lnew(3)=8 - 7 =1>0
C(1)=3>0; C(2)=2>0
Все C(i)>0, состояние системы ненадежное.
3. Lnew(2) = L(2) + a =4+2=6
C(2)=M(2)-Lnew(2)=6 - 6 =0
C(1)=3>0; C(3)=3>0
C(2)=0, состояние системы надежное.
9.
Решение примера (продолжение)Будем выделять остаточный ресурс процессам и оценивать состояние системы.
4. a = 6, после завершения Process (2)
5. Lnew(1) = L(1) + a’ =1+3=4
C(1)=M(1)-Lnew(1)=4 - 4 =0
C(3)=3>0;
C(1)=0, состояние системы надежное.
6. a = 7, после завершения Process (1)
7. Lnew(3) = L(2) + a’ =5+3=8
C(3)=M(3)-Lnew(3)=8 - 8 =0
C(3)=0;
C(3)=0, состояние системы надежное.
8. a = 12, все процессы завершены.
10.
Недостатки алгоритма банкира1. Фиксированное число ресурсов в системе.
2. Фиксированное число процессов в системе.
3. Время реакции ОС на запрос от процесса может слабо
отличаться от «бесконечного».
4. Кто должен определять максимальную потребность в
ресурсах?
5. Возможен переход в однопрограммный режим.
11.
Обнаружение тупиковОбнаружение тупика – установление факта наличия в системе
процессов ожидающих «нереализуемое» состояние.
Основной подход к решению – построение графа распределения
ресурсов и нахождение в нем циклов. Чрезвычайно затратный
подход. На практике в чистом виде не используется.
12.
Восстановление системы после обнаружения тупикаВосстановление работы системы – продолжение работы
некоторых процессов после устранения причины тупика.
Сложности решения:
• Неочевидность тупика.
• Трудно остановить процесс в произвольной точке кода.
• Большие накладные расходы на реализацию сохранения
результатов.
• В системах с большим числом разноприоритетных процессов
трудно удалить процессы с высоким приоритетом.
13.
Виртуализация ресурсов – средство борьбы ступиками
Система не устраняет условий возникновения тупиков – при
возникновении конкурирующих запросов ВСЕ ресурсы могут
быть заменены на «виртуальный аналог».
Особенности решения:
• Алгоритмически простое решение.
• Формально, не боится большого числа процессов.
• Сложность возврата из «виртуального мира» в реальный в
случае иерархической виртуальности.
14.
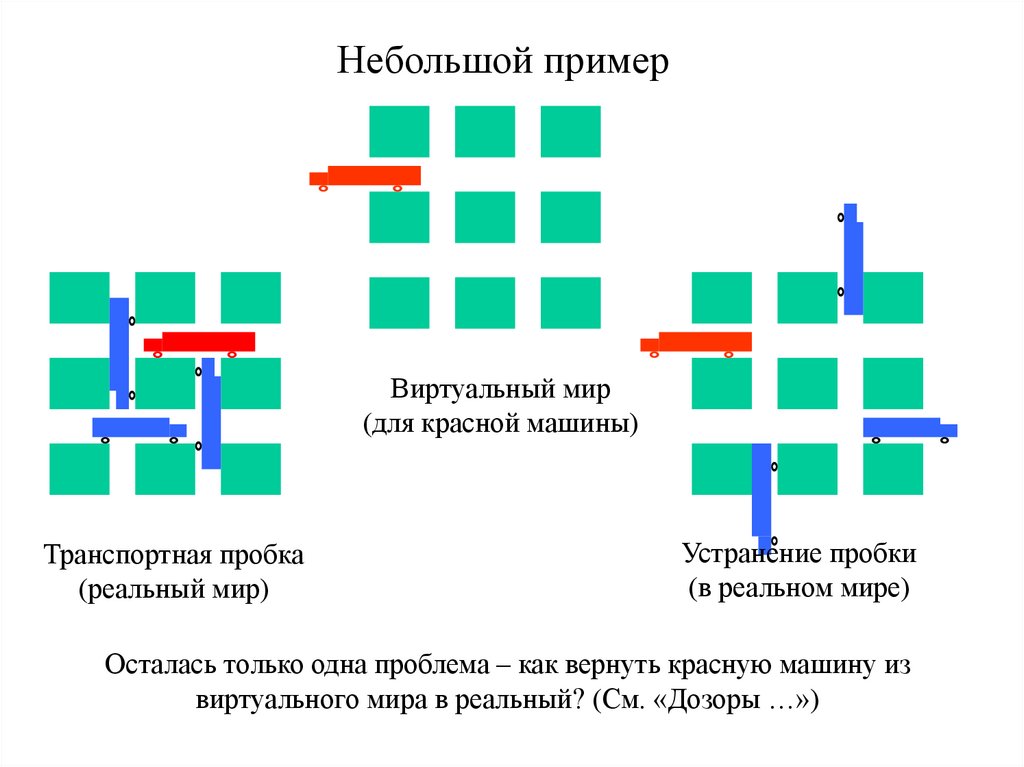
Небольшой примерВиртуальный мир
(для красной машины)
Транспортная пробка
(реальный мир)
Устранение пробки
(в реальном мире)
Осталась только одна проблема – как вернуть красную машину из
виртуального мира в реальный? (См. «Дозоры …»)











 software
software








