Квадратичная функция

1. ОПРЕДЕЛЕНИЕ

Квадратичной функцией называется
функция, которую можно задать
формулой вида у = ах2 + вх + с, где х независимая переменная; а, в, с - некоторые числа, а 0.
График квадратичной функции - парабола.

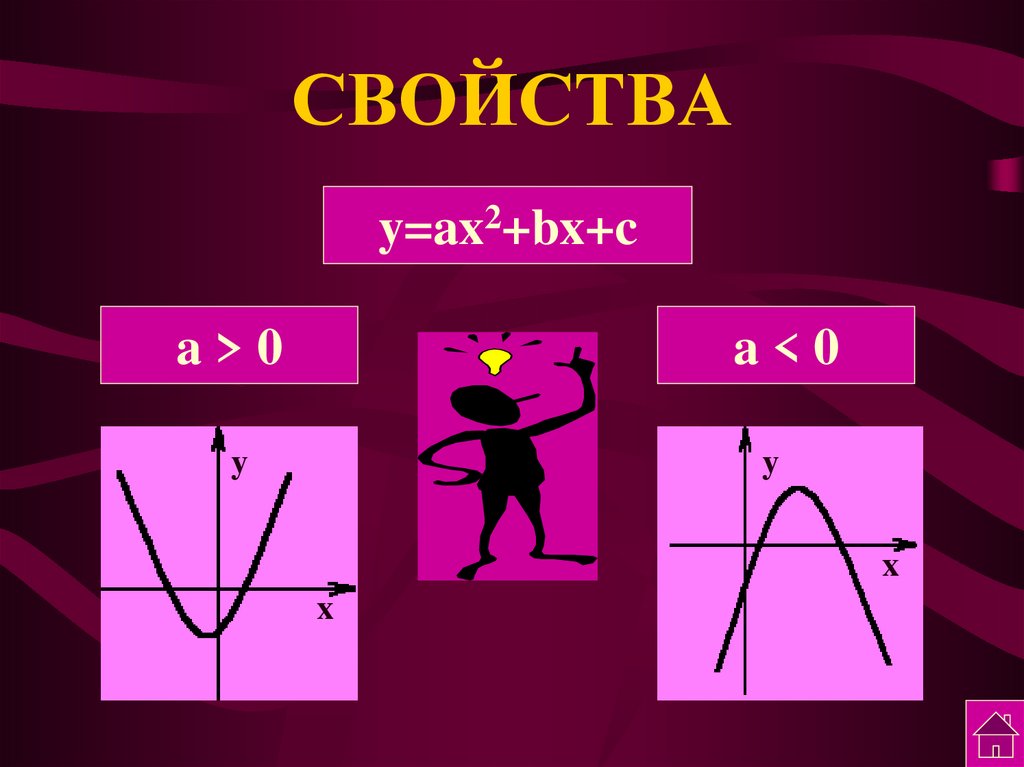
2. СВОЙСТВА

y=ax2+bx+c
a>0
a<0
y
y
x
x

3. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

Область определения
Область значения
Вершина параболы
Направление ветвей
Нули функции
Промежутки возрастания и убывания
Точки пересечения с осями координат

4. ПОСТРОЕНИЕ ГРАФИКА

• Найти координаты вершины параболы
(m;n), где m = - b/2a n = -(b2+4ac)/4a
• Построить дополнительные точки
х
у
m
n
• Соединить плавной линией

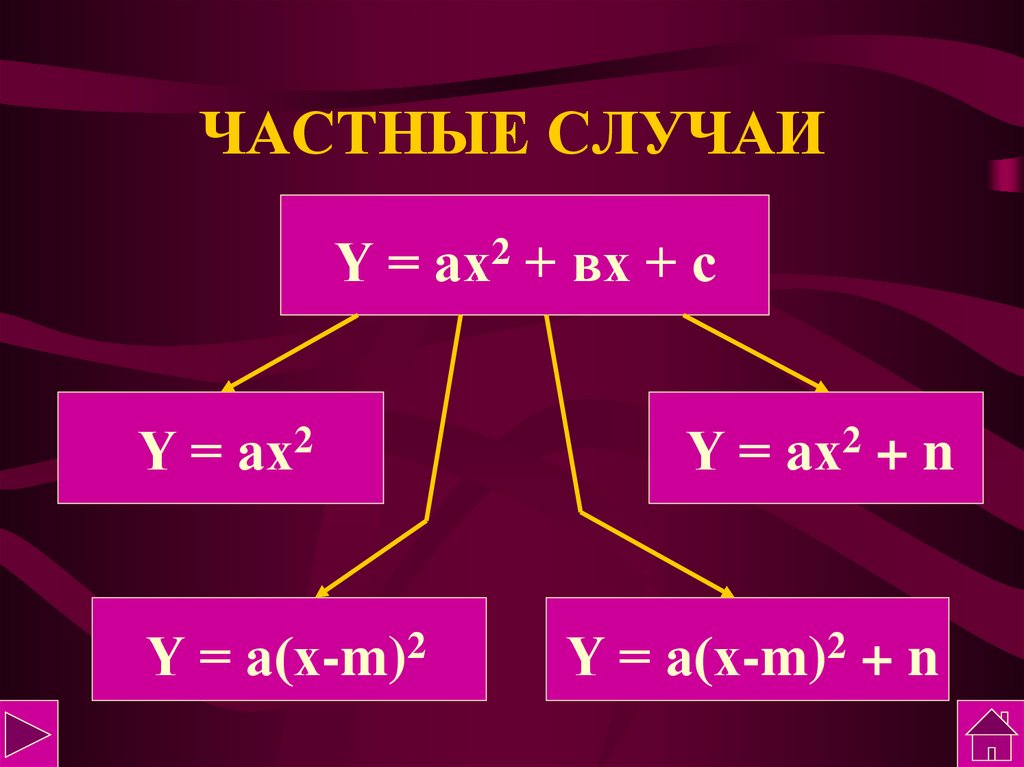
5. ЧАСТНЫЕ СЛУЧАИ

Y = ах2 + вх + с
Y = ах2
Y = а(х-m)2
Y = ах2 + n
Y = а(х-m)2 + n

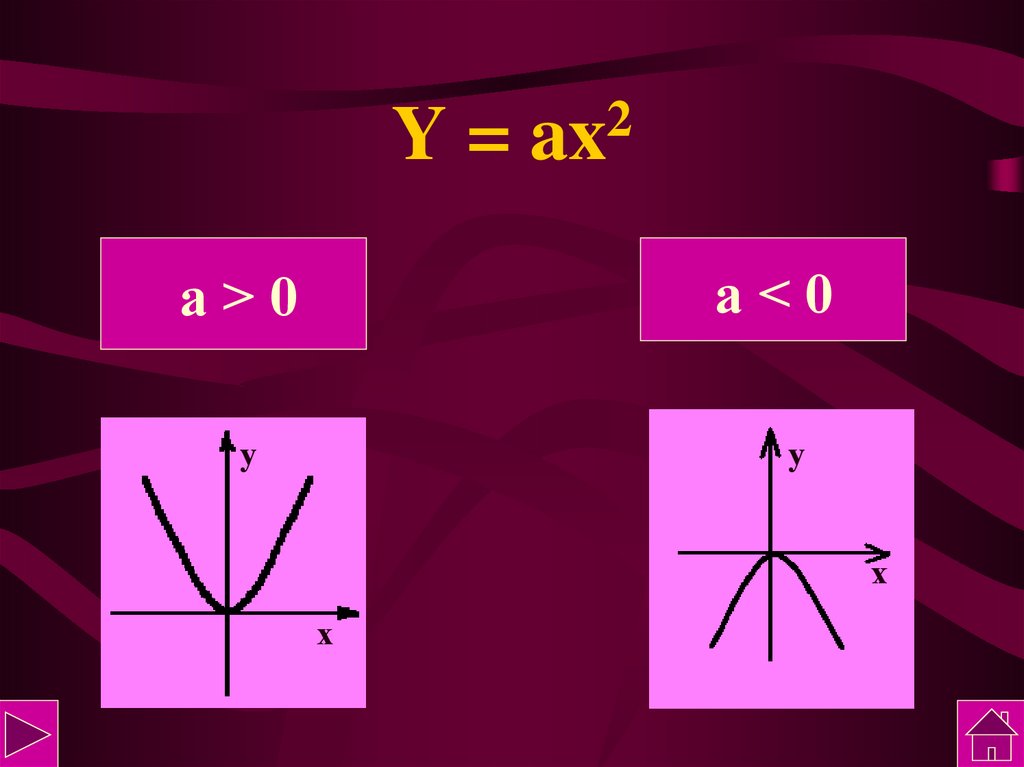
6. Y = ax2

Y=
2
ax
а<0
а>0
у
у
х
х

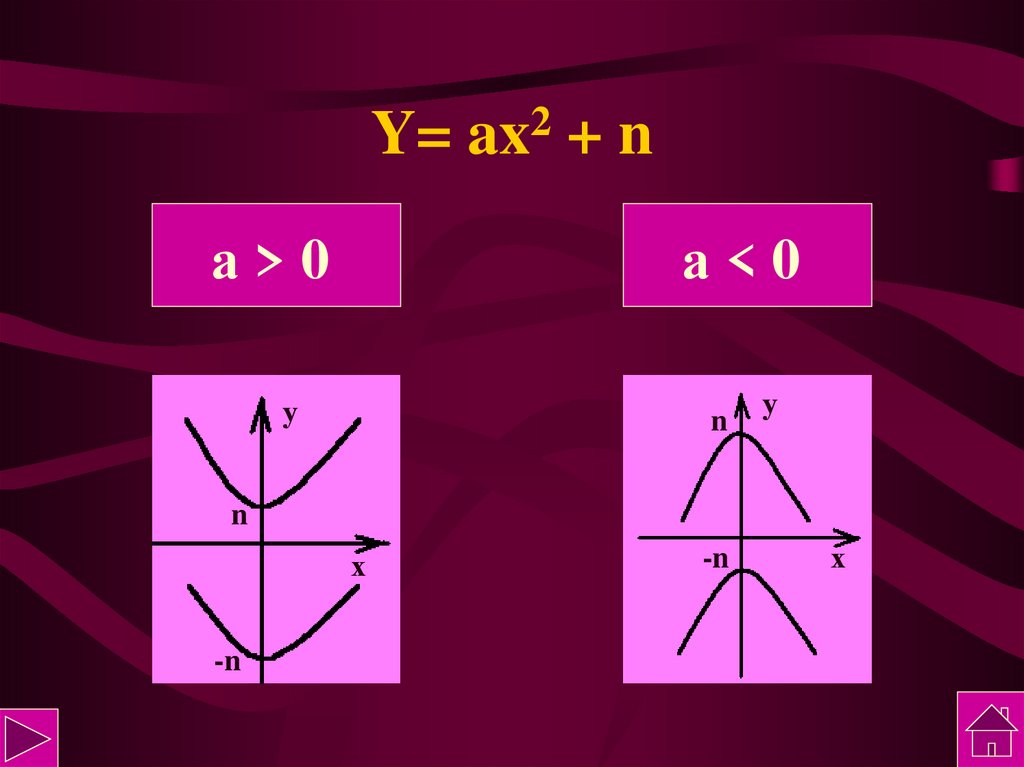
7. Y= ax2 + n

Y=
а>0
2
ax
+n
а<0
у
n
у
n
х
-n
-n
х

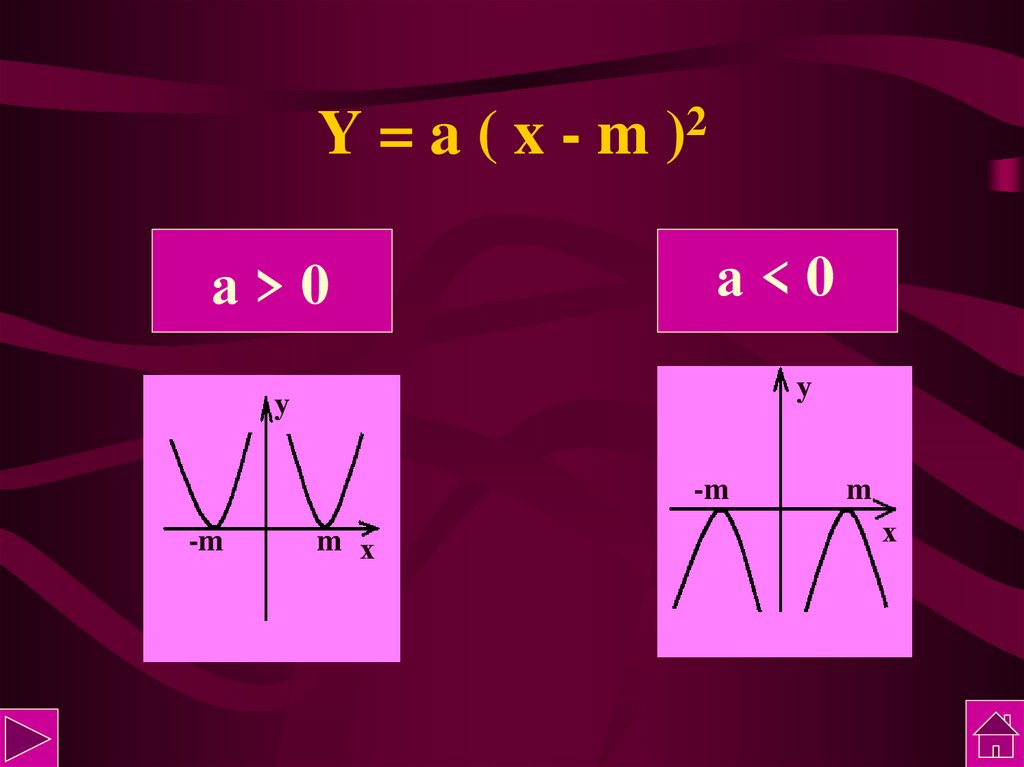
8. Y = a ( x - m )2

Y=a(x-m
а>0
2
)
а<0
у
у
-m
-m
m х
m
х

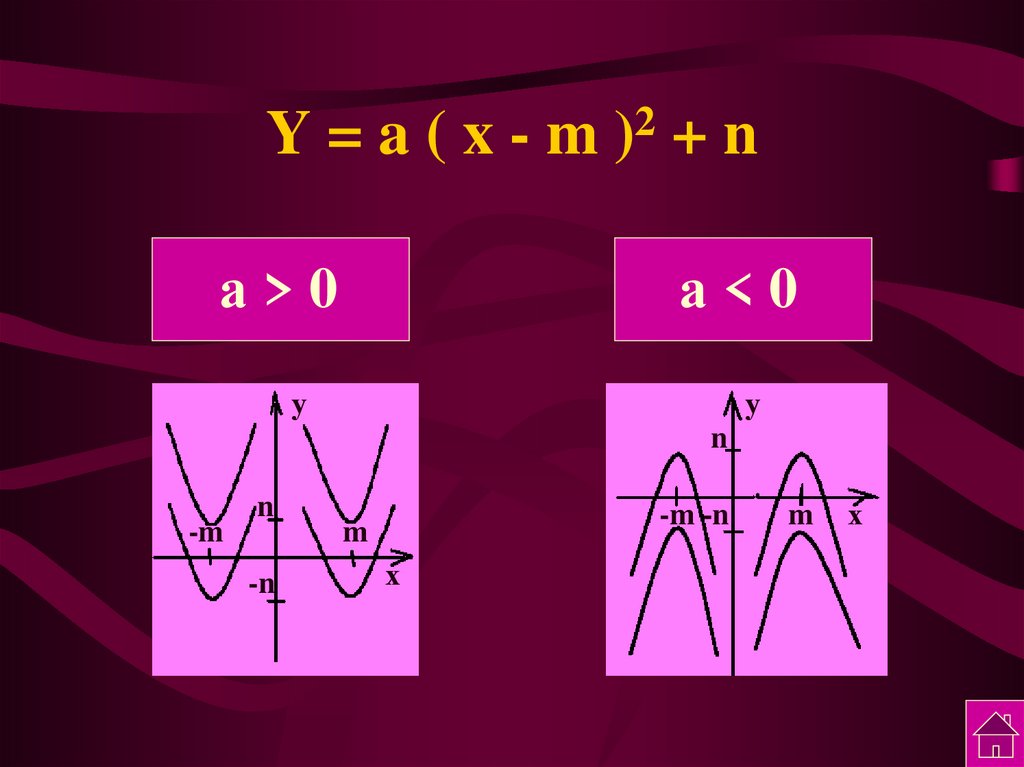
9. Y = a ( x - m )2 + n

Y=a(x-m
а>0
2
)
+n
а<0
у
у
n
-m
n
-n
-m -n
m
х
m
х

10. ОТРАБОТКА НАВЫКОВ

Карточка №1
Используя шаблон параболы у = х2 , построить график
функции у = ( х + 2)2 + 3.
Карточка №2
Постройте график функции у = х2 - 4х +4.
Карточка №3
Исследуйте график функции у = -2х2 -5х -2.