Нахождение гамильтонова контура минимальной длины. Задача коммивояжера

1.

НАХОЖДЕНИЕ ГАМИЛЬТОНОВА КОНТУРА МИНИМАЛЬНОЙ ДЛИНЫ.
ЗАДАЧА КОММИВОЯЖЕРА

2.

Слово «гамильтонов» связано с именем
известного ирландского математика У.
Гамильтона, которым в 1859 году
предложена
следующая
игра
«Кругосветное путешествие». Каждой из
двадцати вершин додекаэдра приписано
название одного из крупных городов
мира. Требуется, переходя от одного
города к другому по ребрам додекаэдра,
посетить каждый город в точности один
раз и вернуться в исходный город.

3.

Граф называется гамильтоновым, если в нем имеется простой цикл,
содержащий каждую вершину этого графа. Сам этот цикл также
называется гамильтоновым.
Эта задача, сводится к отысканию в графе додекаэдра простого цикла,
проходящего через каждую вершину этого графа.

4.

Несмотря на внешнее сходство постановок, задачи
распознавания эйлеровости и гамильтоновости графа
принципиально различны. Легко узнать, является ли
граф эйлеровым и, в случае положительного ответа,
алгоритм Флёри позволяет достаточно быстро
построить один из эйлеровых циклов. Ответить на
вопрос, является ли данный граф гамильтоновым, как
правило, очень трудно.
Практическое применение задача о поиске гамильтонова цикла в графе находит,
например, в задачах распознавания образов. Там вершины графа соответствуют
допустимым символам, а ребра соединяют те символы, которые могут быть соседними.
Самый длинный путь в этом графе будет наилучшим кандидатом для правильной
интерпритации. Поиск самого длинного пути или цикла тесно связан с задачей о
гамильтонове цикле.

5.

Связь задач о гамильтоновом пути и гамильтоновом цикле
Существует простое отношение между задачами нахождения гамильтонова пути и нахождения
гамильтонова цикла. В одном направлении задача о гамильтоновом пути для графа эквивалентна задаче о
гамильтоновом цикле в графе H, полученного из графа G путём добавления новой вершины и соединения её
со всеми вершинами графа G. Таким образом, поиск гамильтонова пути не может быть существенно
медленнее, чем поиск гамильтонова цикла.
В обратном направлении задача о гамильтоновом цикле для графа G эквивалентна задаче о гамильтоновом
пути в графе H, полученном копированием одной вершины v графа G (в v'), то есть вершина v' будет иметь
ту же окрестность, что и v, и добавлением двух вспомогательных вершин степени один, одна из которых
соединена с v, а другая с v'.
Задача о гамильтоновом цикле является также частным случаем задачи коммивояжёра, полученной
установкой всех расстояний между двумя пунктами в единицу, если они смежны, и двум в противном
случае. После решения задачи коммивояжёра следует проверить, что полное расстояние равно n (если так,
маршрут является гамильтоновым циклом, если же гамильтонова цикла нет, кратчайший путь будет длиннее
этой величины).

6.

Задача коммивояжёра
Задача коммивояжёра — одна из самых
известных задач комбинаторной оптимизации,
заключающаяся в поиске самого выгодного
маршрута, проходящего через указанные города
хотя бы по одному разу с последующим
возвратом в исходный город. В условиях задачи
указываются критерий выгодности маршрута и
соответствующие матрицы расстояний,
стоимости и тому подобного.
Как правило, указывается, что маршрут должен
проходить через каждый город только один раз
— в таком случае выбор осуществляется среди
гамильтоновых циклов.

7.

!
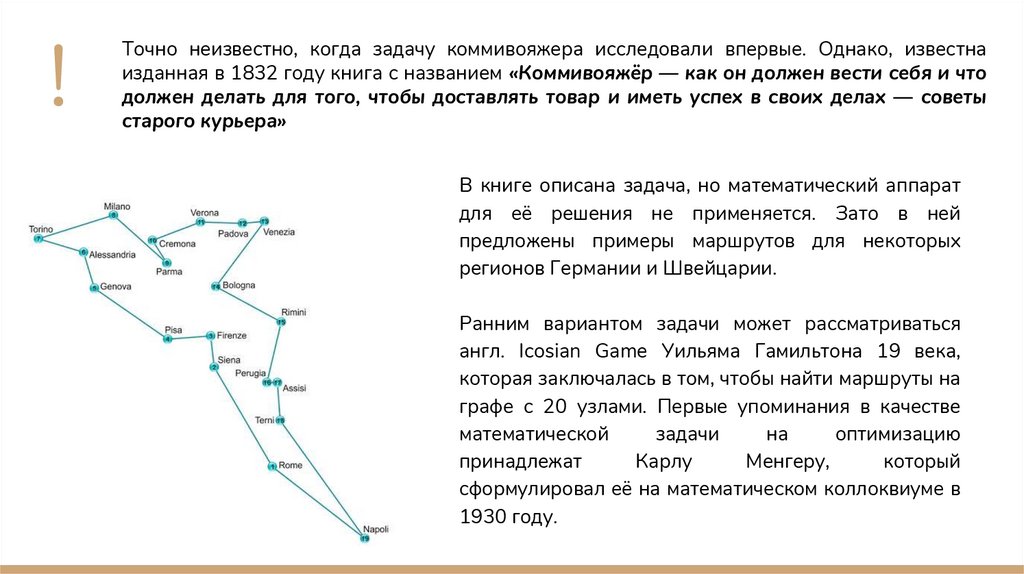
Точно неизвестно, когда задачу коммивояжера исследовали впервые. Однако, известна
изданная в 1832 году книга с названием «Коммивояжёр — как он должен вести себя и что
должен делать для того, чтобы доставлять товар и иметь успех в своих делах — советы
старого курьера»
В книге описана задача, но математический аппарат
для её решения не применяется. Зато в ней
предложены примеры маршрутов для некоторых
регионов Германии и Швейцарии.
Ранним вариантом задачи может рассматриваться
англ. Icosian Game Уильяма Гамильтона 19 века,
которая заключалась в том, чтобы найти маршруты на
графе с 20 узлами. Первые упоминания в качестве
математической
задачи
на
оптимизацию
принадлежат
Карлу
Менгеру,
который
сформулировал её на математическом коллоквиуме в
1930 году.

8.

Будем считать, что задача коммивояжера задана в виде матрицы. Для получения оценки
снизу длин множества всех гамильтоновых контуров воспользуемся тем, что в каждый
гамильтонов контур входит только по одному элементу из каждой строки и из каждого
столбца матрицы расстояний. Если элементы любой строки или любого столбца
уменьшить на какое-либо число, то на это же число уменьшаются длины всех
гамильтоновых контуров. Приведение матрицы может производиться по строкам и по
столбцам.
При этом длины всех
гамильтоновых контуров
уменьшаются на сумму
вычтенных из каждой
строки чисел, то есть на
величину
,
оставаясь в то же время
неотрицательными.

9.

Уточненная оценка снизу длин гамильтоновых контуров определяется в виде:
Метод приведения матрицы расстояний будем применять и далее для
получения оценок снизу различных подмножеств множества гамильтоновых
контуров.

10.

Для возможности применения математического аппарата для
решения задачи её следует представить в виде математической
модели. Задачу коммивояжёра можно представить в виде модели
на графе, то есть, используя вершины и ребра между ними. Таким
образом, вершины графа соответствуют городам, а рёбра между
вершинами. Каждому ребру можно сопоставить критерий
выгодности маршрута, который можно понимать как, например,
расстояние между городами, время или стоимость поездки.
Гамильтоновым циклом называется маршрут, включающий ровно по одному разу каждую вершину
графа.
В целях упрощения задачи и гарантии существования маршрута обычно считается, что модельный
граф задачи является полностью связным. В тех случаях, когда между отдельными городами не
существует сообщения, этого можно достичь путём ввода рёбер с максимальной длиной. Из-за
большой длины такое ребро никогда не попадет к оптимальному маршруту, если он существует.
Таким образом, решение задачи коммивояжёра — это нахождение гамильтонова цикла
минимального веса в полном взвешенном графе.

11.

Конечно, для решения этой задачи существует простой алгоритм – полный перебор всех
возможных вариантов. Однако, такой подход, как правило, неприемлем из-за
чрезвычайно большого числа этих вариантов (если число городов равно n, то число всех
возможных обходов nn). Поэтому вызывает интерес не просто алгоритм, а эффективный
алгоритм.

12.

СПАСИБО ЗА ВНИМАНИЕ!