Similar presentations:
3D-моделирование. Виды моделей
1. 3D-моделирование Виды моделей
Лаборатория графических систем,кафедра НГ, МГ и теоретических основ САПР,
ННГАСУ
Лекция
3D-моделирование
Виды моделей
Проектирование с
использованием
современных систем
CAD/CAM/CAE
2.
геометрическое моделирование –это весь многоступенчатый процесс создания
модели объекта –
от вербального описания объекта в
техническом задании на его проектирование
и изготовление
до получения данных в электронном виде.
3.
Под геометрическими моделями в САПР иАСНИ понимают данные о геометрии
проектируемого объекта, включающие в себя
размеры, координаты, масштабы, связи
геометрических элементов и т.д. Кроме
геометрической информации, в модели могут
быть включены технологические данные
(обозначения, текстовые пояснения и т.п.)
4. Виды моделей
ТочечнаяКаркасная
Граничная
Конструктивная
Воксельная
5. точечная модель
Точечной моделью (ТМ) геометрического объектаназывается совокупность
ТM = { V, A }, где
V - вектор координат Xi, Yi, Zi вершин объекта, где i =
1,…,n;
A - информационный массив атрибутов вершин Vi.
Совокупность точек Тi
называется облаком точек.
Применяется в технологиях
бесконтактных измерений
6. каркасная модель
Каркасной моделью (КМ) геометрического объектаназывается совокупность
KM = { V, R, A }, где
V - вектор координат Xi, Yi, Zi вершин объекта, где i = 1,…,n;
R - информационный массив, содержащий данные о ребрах
Rij, соединяющих вершины Vi и Vj объекта.
A - информационный массив атрибутов вершин Vi и ребер Rij.
Каждому ребру может быть поставлен в соответствие
квалификационный признак (атрибут), характеризующий данное ребро:
линейное или нелинейное, коэффициенты уравнений линий –
носителей ребер, каким типом линии, согласно ГОСТ 2.305-68 [17],
изображаются проекции ребра (основная, штриховая, штрихпунктирная, волнистая и т.д.), толщина изображающих проекции линий
(основная, тонкая, утолщеная), цвет линий.
7. Формирование каркасной модели на основе точечной
ТкRij
Тj
Установление связи
между Ti и Tj: Rij (Тi, Tj, A)
8.
Достоинством каркасной модели являются малыйобъем хранимых данных и быстрота получения
проекционного изображения.
Недостатком является неоднозначность
генерируемого проекционного изображения, и,
как следствие, возможность ошибочных
интерпретаций результатов проектирования, а
также невозможность решения каких - либо
прикладных инженерных задач, в том числе при
формировании изображений для чертежноконструкторской документации.
9. граничная модель
Граничной моделью (ГМ) пространственногообъекта называется совокупность
ГМ = { G, V, R, A }, где
V, R - информационные массивы, используемые в КМ,
G - информационный массив граней (отсеков пов-cтей ),
где грань Gi = {( V1i, V2i, V3i, ... Vni) , где
V1i, …, Vni V} задается своими вершинами,
перечисленными в порядке обхода грани против часовой
стрелки. При этом грань Gi может охватывать как
односвязную, так и неодносвязную область без
самопересечений.
A - информационный массив атрибутов вершин Vi, ребер
Rij и граней Gi, куда, в свою очередь входят следующие
массивы:
10.
F - информационный массив, содержащийкоэффициенты уравнений Fi (x, y, z) = 0
поверхностей, которые являются носителями
граней Gi;
L – информационный массив, содержащий
коэффициенты уравнений Lij (x, y, z) = 0
кривых 1 или 2 порядка, которые являются
носителями ребер Rij.
Остальными атрибутами могут быть те же
признаки, что и в КМ, а также текстура
(материал покрытия и раскраски) граней
поверхности и т.п.
11. n
Трёхгранник Френеn
n – нормаль, - бинормаль, - касательная
12.
Формирование граничной моделиni
Тi
Rij
Тj
13.
Граничная модель даёт возможностьрешения практически любой прикладной
задачи в геометрическом моделировании
(например, решить задачу видимости линий
на изображении объекта, подсчитать массинерционные характеристики и т. д.)
14. конструктивная модель
Конструктивной моделью называется совокупностьСМ = {G(R), B(M), A}, где
G(R) - граф сборки конструкции, либо бинарная древовидная
структура , определяющие порядок и характер взаимодействия
составляющих объектов,
R - ребра графа, атрибутами которого могут быть параметры формы и положения i-ой
модели относительно j-ой модели и знаки теоретико-множественных операций:
объединения, вычитания и пересечения.
Параметрами формы могут быть числовые значения масштабных коэффициентов по
каждой из осей в отдельности либо по всем трем осям сразу.
Параметрами положения могут быть вектор переноса Т, вектор поворота Е, задающий
углы поворота i-го объекта на заданные углы относительно координатных осей.
В(М) - банк моделей объектов, каждый из которых может быть
как непроизводной , так и составной фигурой. Каждой модели
поставлено в соответствие символическое имя, по которому идет
поиск информации, и имя файла, в котором хранится вся
информация, относящаяся к модели.
А - атрибуты моделей (материал, плотность, цвет и т.д.)
15.
Модель материального тела иликонструктивная (constructive solid geometry,
CSG) модель дает возможность определить
качественные характеристики объекта, из
каких элементарных частей состоит тело и
т.д.
Имея набор граничных моделей и
информацию о связях между ними, можно
получать конструктивные модели сложных
объектов.
16.
Рис.1 Пример входной информации, созданной в редакторе ГНОМдля получения трёхмерной модели геометрического объекта в
модуле ОБРАЗ пакета КИТЕЖ.
17.
Рис.2 Результат визуализации 3D модели,синтезированной по исходной информации,
данной на рис.1
18.
Рис.7 Пример информации, не позволяющей однозначновосстановить 3D образ пространственного объекта
19.
Рис.4 Объекты, удовлетворяющие чертежу,показанному на рис.3
20. алгоритм синтеза модели по проекциям
анализ проекций;создание массивов 3-х мерных координат;
поиск и удаление ложных геометрических
элементов (ЛГЭ);
создание возможных каркасов;
создание граничных моделей;
создание конструктивных моделей.
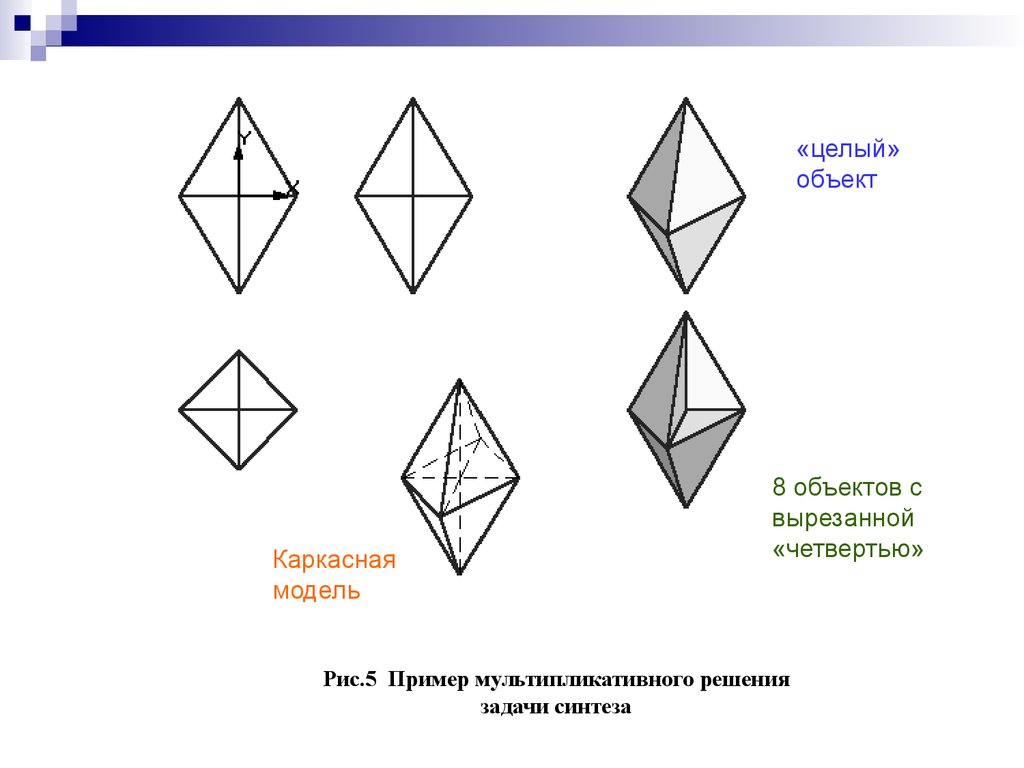
21.
«целый»объект
Каркасная
модель
8 объектов с
вырезанной
«четвертью»
Рис.5 Пример мультипликативного решения
задачи синтеза
22.
Непроизводной фигурой (НФ) – называетсяпространственное тело, которое в данном
классе задач рассматривается как единое и
неделимое.
призма
цилиндр
пирамида
конус
шар
Рис.6
Примеры НФ
23.
Составной фигурой (СФ) – называется 3D-объект,созданный с применением аппарата теоретикомножественных операций:
объединения ( ),
пересечения ( ),
вычитания ( / )
Рис.7
Пример СФ
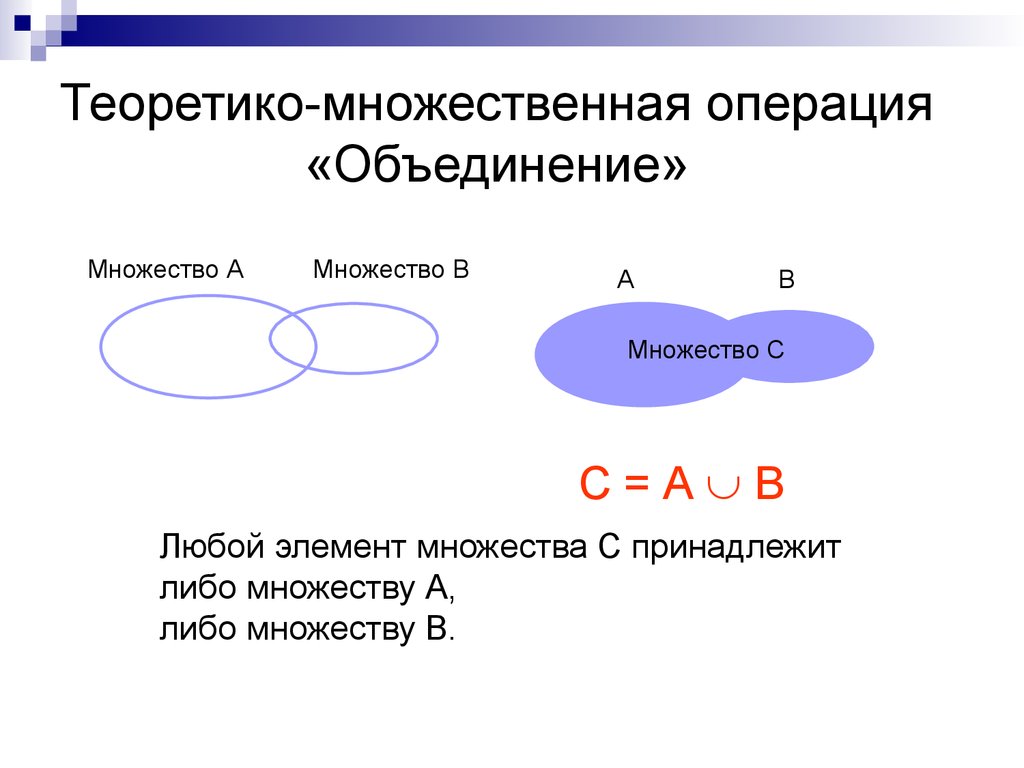
24. Теоретико-множественная операция «Объединение»
Множество АМножество В
А
В
Множество С
С=А В
Любой элемент множества С принадлежит
либо множеству А,
либо множеству В.
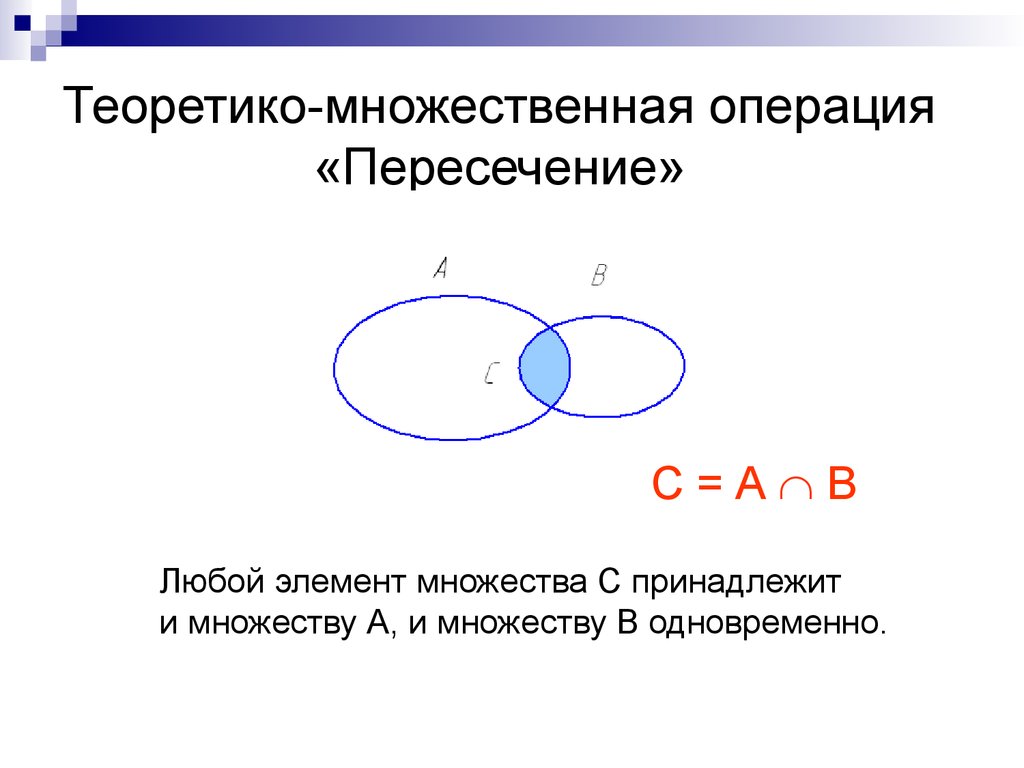
25.
Теоретико-множественная операция«Пересечение»
С=А В
Любой элемент множества С принадлежит
и множеству А, и множеству В одновременно.
26.
Теоретико-множественная операция«Вычитание»

























 management
management software
software








