Алгоритмы поиска подстроки в строке. Лекция 6

1.

АЛГОРИТМЫ ПОИСКА
ПОДСТРОКИ В СТРОКЕ
СТРОКА в которой осуществляется
поиск называется ТЕКСТОМ
• СТРОКА, которую необходимо найти
называется ПОДСТРОКОЙ ПОИСКА
(ОБРАЗОМ)
1

2. ПРЯМОЙ ПОИСК

самый простой и не эффективный
поиск.
не проводит анализа подстроки
наиболее эффективно работает при
небольшом количестве совпадений при
очередном сравнивании символов
образа с символами текста
2

3. ПРЯМОЙ ПОИСК

п р и ме р
т е к с т а
д л я
п о и с к а
т е к с т а
д л я
п о и с к а
т е к с т а
д л я
п о и с к а
т екст
п р и ме р
т екст
п р и ме р
т екст
3

4. ПРЯМОЙ ПОИСК

п р и ме р
т екс
т ек
т е
т
т е к с т а
т
с
к
е
т
д л я
п о и с к а
т
ст
кст
екст
4

5. ПРЯМОЙ ПОИСК

S – текст, n – количество символов текста
O – образ, m – количество символов
образа
i =0; j=0;
пока (i<n) нц
j=0; f=0;k=i;
пока (j<m и k<n и S[k]==O[j]) нц
k++; j++;f++;
кц
5

6. ПРЯМОЙ ПОИСК

если f==m то УСПЕХ, вернуть i;
i++;
кц
6

7. ПРЯМОЙ ПОИСК

Самый неэффективный случай:
а а а а а а а а а а а а а а а а а а а а а а а в
а а а а а в
Оценка времени работы алгоритма O(n*m)
7

8. Алгоритм Кнута, Морриса и Пратта

Описан Кнутом и Праттом и независимо
от них Моррисом
Результаты опубликованы совместно в
1977 г.
Алгоритм назвали КМП-алгоритмом
Временная характеристика алгоритма
O(n)
8

9. Алгоритм Кнута, Морриса и Пратта

для повышения эффективности
алгоритма необходимо, чтобы сдвиг на
каждом шаге алгоритма был
максимально возможным
авс д
авс е
авс е
для вычисления этого сдвига алгоритм
разбит на две части:
9

10. КМП - АЛГОРИТМ

1) предварительная обработка подстроки
2) поиск подстроки
авс д
авс е
авс е
обозначим j - количество совпадений,
текущего сравнения (j = 3)
значение j зависит только от вида
образа, никак не зависит от текста
10

11. КМП – АЛГОРИТМ. Предварительная обработка образа

Для образа строится таблица сдвигов
d[m]
d[0] = -1, d[1] = 0
d[j] – длина самой длинной
последовательности символов образа,
предшествующих j, которая полностью
совпадает с началом образа
При j совпадениях образа с текстом
можно выполнить сдвиг на j – d[j]
11

12. КМП – АЛГОРИТМ. Предварительная обработка образа

Примеры таблиц сдвигов для различных
образов:
АБВГ
d[0]=-1
d[1]=0
d[2]=0
d[3]=0
АБАБВ
d[0]=-1
d[1]=0
d[2]=0
d[3]=1
d[4]=2
АБАБВА
d[0]=-1
d[1]=0
d[2]=0
d[3]=1
d[4]=2
d[5]=2
12

13. КМП – АЛГОРИТМ. Предварительная обработка образа

m = длина образа о;
j = 1, k=0
d[0] = -1;
d[1] = 0;
Пока j<m-1 нц
Пока o[k]!=o[j] и j<(m-1) нц
d[j+1] = d[j]; j++; кц
13

14. КМП – АЛГОРИТМ. Предварительная обработка образа

Если j==m-1 то закончить выполнение
цикла
k++;
d[j+1]=k;
j++;
кц
14

15. КМП – АЛГОРИТМ. Пример

a b c а b d
d -1 0 0 0 1 2
сдвиг на j – d[j]
a b c a b c a a b c a b a b c b a b c a b d
a b c а b d
5 совпадений, сдвиг 5 – 2 = 3
a b c а b d 4 совпадения, сдвиг 4 – 1 = 3
a b c а b d 1 совпадение, сдвиг 1 – 0 = 1
a b c а b d 5 совпадений, сдвиг 3
a b c а b d 2 совпадения,
сдвиг 2
15

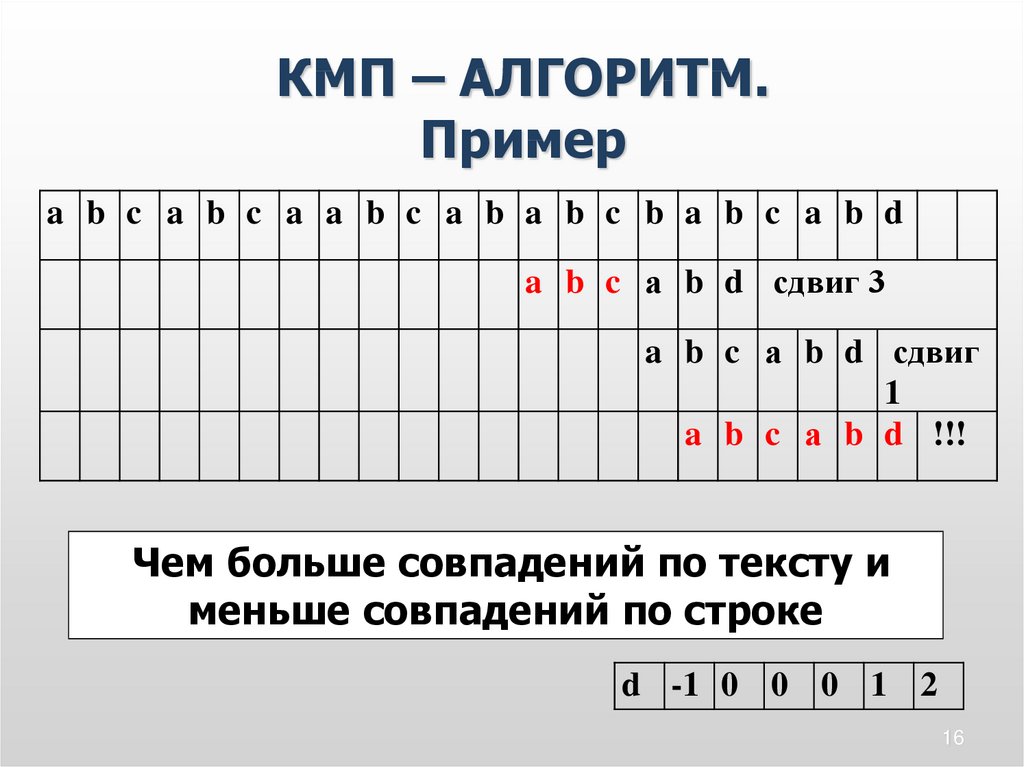
16. КМП – АЛГОРИТМ. Пример

a b c a b c a a b c a b a b c b a b c a b d
a b c а b d сдвиг 3
a b c а b d сдвиг
1
a b c а b d !!!
Чем больше совпадений по тексту и
меньше совпадений по строке
d -1 0 0 0 1 2
16

17. Алгоритм Боуэра-Мура

Предложен в 1977
a b c а b d
a b c a b f a a b c a b a b c b a b c a b d
a b c а b d
a b c а b d
a b c а b d
17

18. Алгоритм Боуэра-Мура

Сравнение символов образа с
символами текста осуществляется с
конца образа
Если несовпадение произошло на
символе, не встречающемся в образе
выполняется сдвиг на длину образа
минус количество совпадений
18

19. Алгоритм Боуэра-Мура

Если несовпадение произошло на
символе, встречающемся в образе, то
выполняется сдвиг на величину, равную
расстоянию от совпавшего символа до
конца образа минус количество
совпадений
Если получен отрицательный или
нулевой сдвиг, осуществляется сдвиг на
1
19

20. Алгоритм Боуэра-Мура

Перед работой создается массив d,
размерность которого равна размеру
использованного алфавита
20

21. Алгоритм Боуэра-Мура. Пример

a b c а b d
d 2 1 3 0 6 6
a b c d e …
a b c a b c a a b c a b a b c b a b c a b d
a b c а b d
a b c а b d
a b c а b d
a b c а b d
21

22. Алгоритм Боуэра-Мура. Пример

a b c a b c a a b c a b a b c b a b c a b d
a b c а b d
a b c а b d
a b c а b d
a b c а b d
Чем меньше совпадений, тем быстрее
22

23. ПОИСК ПОДСТРОКИ В СТРОКЕ

Определить таблицы сдвигов для КМПалгоритма и алгоритма Боуэра – Мура
На каждом шаге выбирать лучший сдвиг
23

24. ПОИСК В МАССИВЕ

Неупорядоченный массив – прямой
поиск (O(n))
Упорядоченный массив – бинарный
поиск (О(log2 n))
24

25. Бинарный поиск

Вход – X[n], a
1. F = 0, L = n-1
2. Если F>L то вернуть -1
3. M =1/2* (F+L)
4. Если X[M] = a, то вернуть M
иначе если X[M]>a то L = M-1
иначе F = M+1
5. Перейти на шаг 2
25

26. Интерполяционный поиск

M =1/2* (F+L) F + 1/2*(L-F)
Если искомый элемент S:
1/2 (S-X[F])/(X[L] – X[F])
Используется алгоритм бинарного поиска
26

27.

BST - деревья
Binary Search Tree - деревья двоичного
поиска.
Родитель
Левый
потомок
Правый
потомок
27

28.

BST - деревья
Правила организации элементов:
Родитель
Родитель >
Левый
потомок
Родитель <=
Правый
потомок
28

29.

BST - деревья
Реализация описания узла дерева в
Си
typedef struct node{
int data;
struct node *left;
struct node *right;
} Node;
29

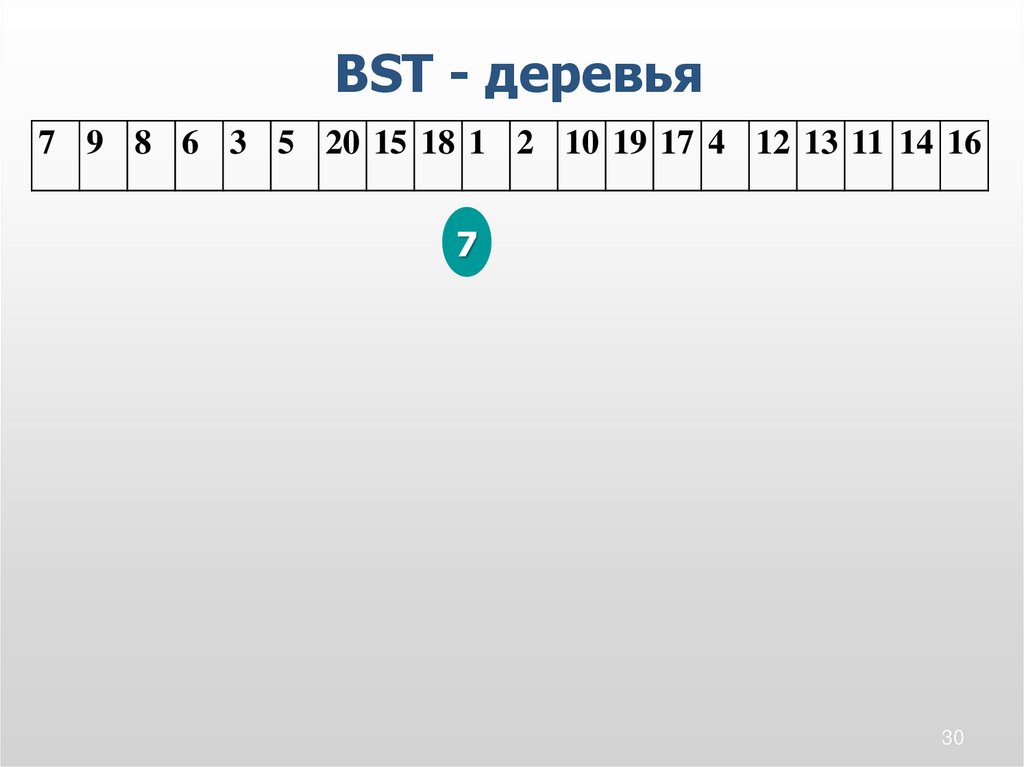
30.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
30

31.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
31

32.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
8
32

33.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
8
33

34.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
3
8
34

35.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
8
3
5
35

36.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
8
3
20
5
36

37.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
5
15
37

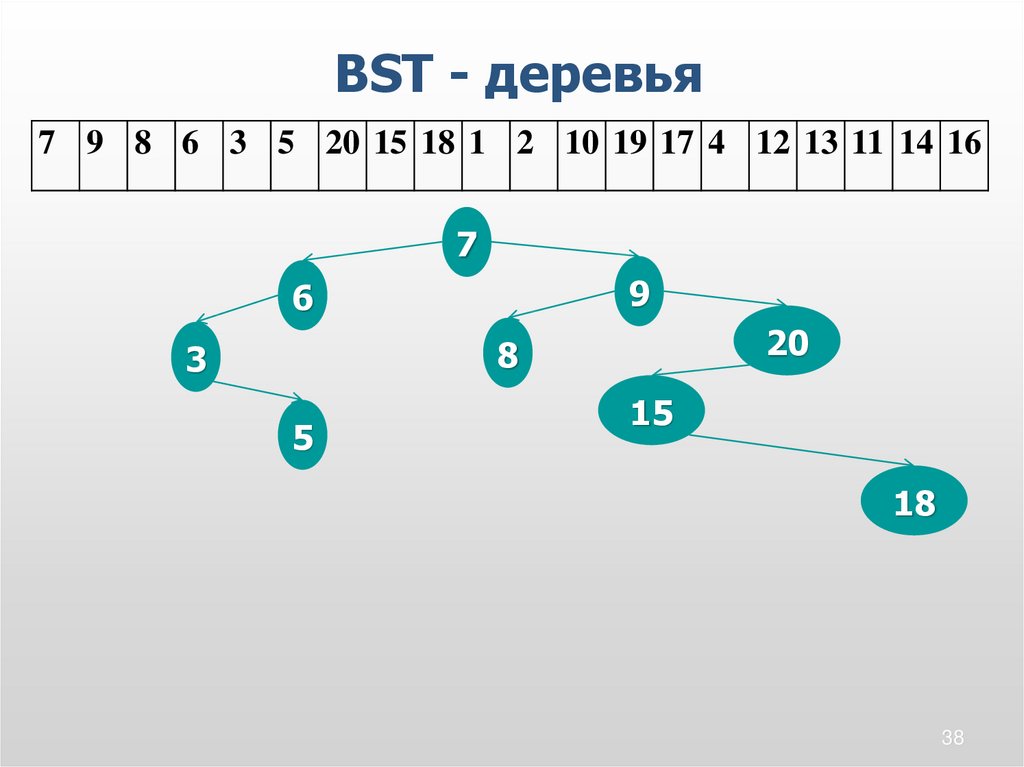
38.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
5
15
18
38

39.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
20
8
3
5
15
18
39

40.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
5
2
20
8
3
15
18
40

41.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
15
5
2
20
8
3
10
18
41

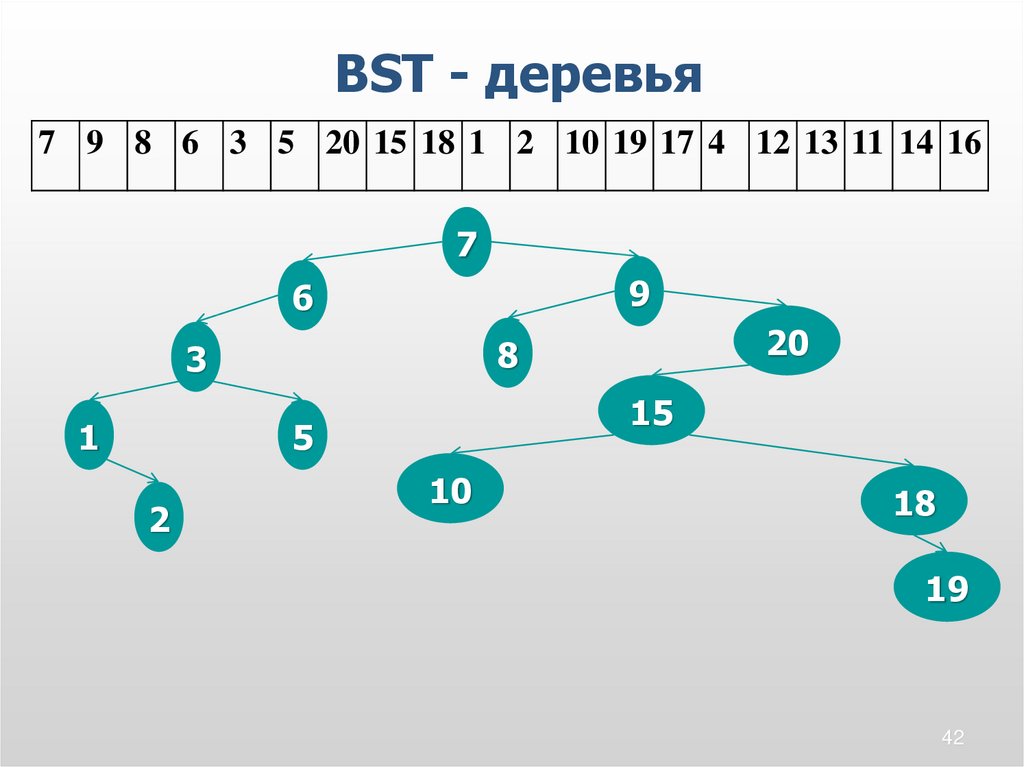
42.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
15
5
2
20
8
3
10
18
19
42

43.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
15
5
2
20
8
3
10
18
17
19
43

44.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
1
15
5
2
20
8
3
4
10
18
17
19
44

45.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
1
15
5
2
4
10
18
12
17
19
45

46.

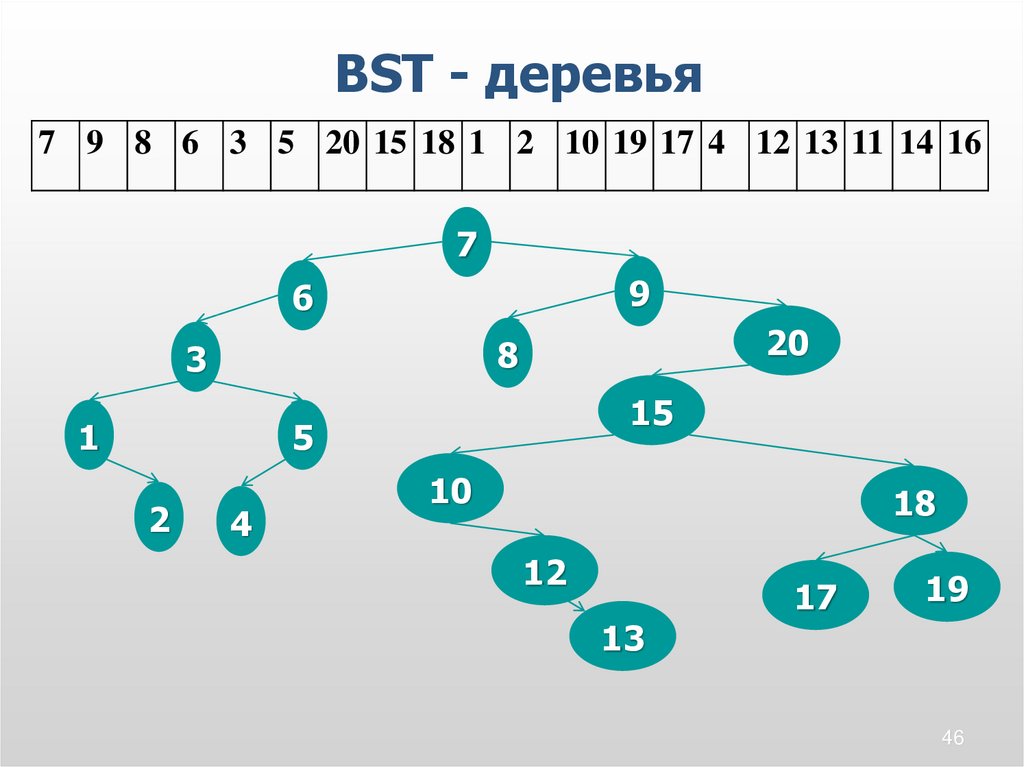
BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
1
15
5
2
4
10
18
12
13
17
19
46

47.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
1
15
5
2
4
10
18
12
11
13
17
19
47

48.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
1
15
5
2
4
10
18
12
11
17
13
19
14
48

49.

BST - деревья
7 9 8 6 3 5 20 15 18 1 2 10 19 17 4 12 13 11 14 16
7
9
6
20
8
3
1
15
5
2
4
10
18
12
11
17
13
14
19
16
49

50.

Пример использования BSTдеревьев для поиска слов
Деревья бинарного поиска можно определить
таким образом чтобы индексы строились в
точности так же…
Деревья – 1
бинарного – 9
поиска – 19
можно – 26
определить – 32 таким – 43
образом – 49
чтобы – 58
индексы – 64
строились – 71
в – 81
точности – 83
так – 92
же – 96
50

51.

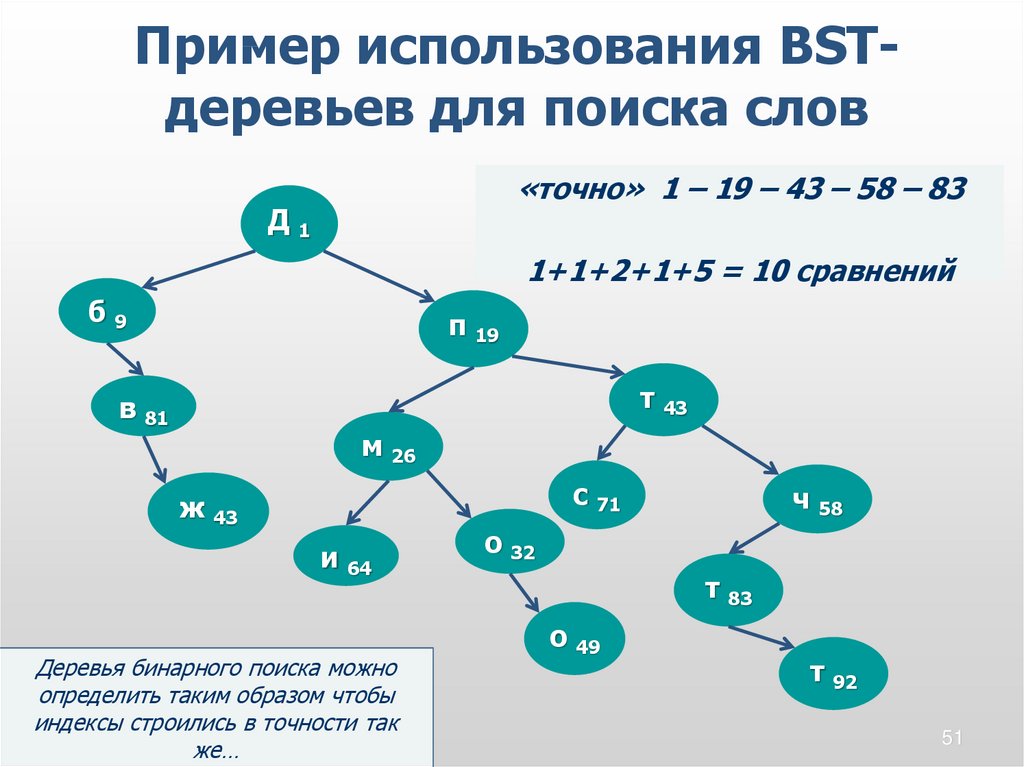
Пример использования BSTдеревьев для поиска слов
«точно» 1 – 19 – 43 – 58 – 83
Д1
1+1+2+1+5 = 10 сравнений
б9
п 19
т 43
в 81
м 26
с 71
ж 43
и 64
Деревья бинарного поиска можно
определить таким образом чтобы
индексы строились в точности так
же…
ч 58
о 32
т 83
о 49
т 92
51

52.

BST – деревья. Алгоритм вставки
элемента
Вставка (Node ** Root, int key)
Если *Root - пустой, то
выделить память
под *Root
*Root -> data = key
*Root -> left = Null
*Root->right = Null
return
52

53.

BST – деревья. Алгоритм вставки
элемента
иначе
Если key >= *Root->data то
Вставка (*Root->right, key)
иначе
Вставка (*Root->left, key)
конец
53

54.

BST – деревья. Алгоритм вставки
элемента. Не рекурсивная
реализация
Вставка1 (Node ** Root, int key)
Если *Root – пустой то выделить память
под *Root
*Root -> data = key
*Root -> left = Null
*Root->right = Null
return
54

55.

BST – деревья. Алгоритм вставки
элемента. Не рекурсивная
реализация
Node *temp = *Root;
Пока (temp не пуст) нц
Если (key>=temp->data) то
Если (temp->right - пуст) то
выделить память под temp->right
temp->right ->left = NULL
temp->right->right = NULL
temp->right->data = key
return
иначе temp = temp->right;
55

56.

BST – деревья. Алгоритм вставки
элемента. Не рекурсивная
реализация
иначе Если temp->left – пуст то
выделить память под temp->left
temp->left->left = NULL;
temp->left->right = NULL;
temp-> left->data = key;
return;
иначе temp = temp->left;
кц
конец
56