Similar presentations:
Площадь. Равновеликие и равносоставленные фигуры
1. Тема: Площадь. Равновеликие и равносоставленные фигуры
Может ли неравное статьравным?
2. Понятие площади фигуры и её измерение.
Узнаете:• Что такое площадь.
• Свойства площади.
• Какие фигуры называют
равными.
• Какие фигуры называют
равновеликими.
• Какие фигуры называют
равносоставленными.
Вспомните:
• Единицы измерения
площади.
• Формулу площади
прямоугольника, квадрата.
• Какая величина называется
скалярной.
• Что такое палетка?
3.
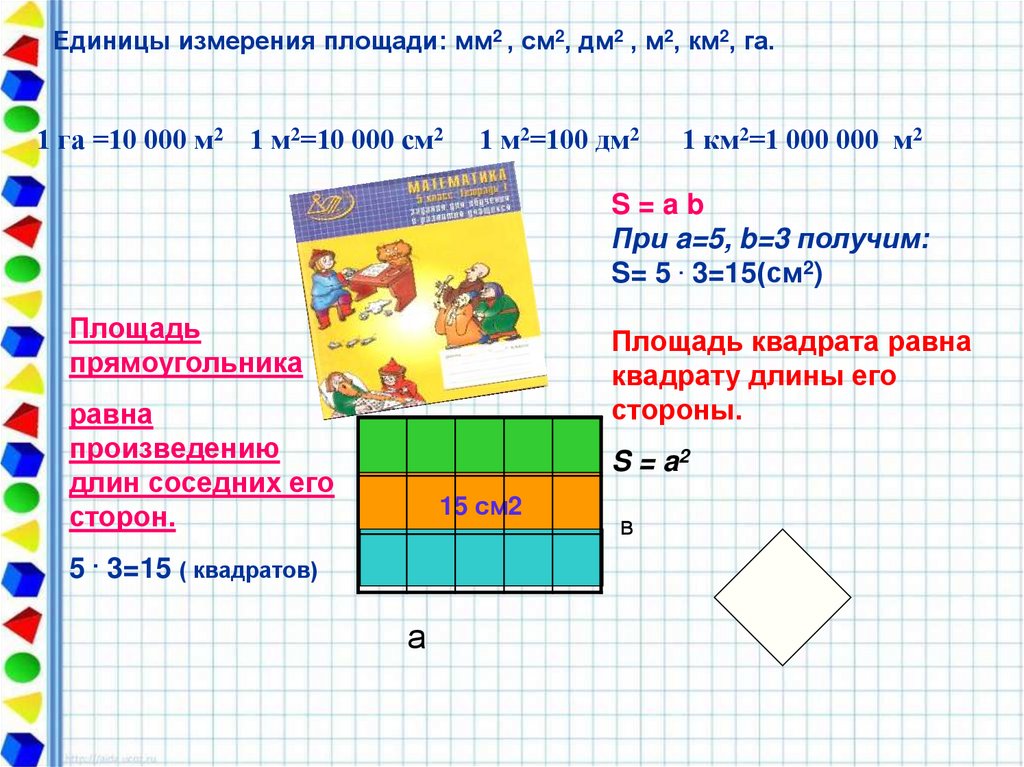
Единицы измерения площади: мм2 , см2, дм2 , м2, км2, га.1 га =10 000 м2 1 м2=10 000 см2
1 м2=100 дм2
1 км2=1 000 000 м2
S=ab
При a=5, b=3 получим:
S= 5 . 3=15(см2)
Площадь
прямоугольника
Площадь квадрата равна
квадрату длины его
стороны.
равна
произведению
длин соседних его
сторон.
S = a2
15 см2
5 . 3=15 ( квадратов)
а
в
4. Величина, которая определяется одним численным значением, называется скалярной величиной. (длина, площадь, объем, масса, время,
стоимость иколичество)
Инструмент, с помощью которого находят приближенное
значение площади, называется палеткой.
S = ab
15 см2
b
При a=5, b=3
получим:
1см
а
S= 5 . 3=15(см2)
5.
Площадью фигуры называетсянеотрицательная скалярная величина,
определенная для каждой фигуры так, что:
1) Равные фигуры имеют равные площади;
2) Если фигура состоит из двух частей, то ее
площадь равна сумме площадей этих
частей
1 см2
7 см2
6. Свойства площадей плоских фигур.
1. Если фигуры равны, то равны численные значения ихплощадей, т. е. F1 = F2 ⇒ S(F1)=S(F2)
2. Если фигура F состоит из фигур F1 и F2 , то численное
значение площади фигуры равно сумме численных значений
площадей фигур F1 и F2 ,т.е. S(F1⊕F2)=S(F1)+S(F2)
3. Численное значение площади единичного квадрата
принимается равным 1, т.е. S(E) =1.
4. При замене единицы площади численное значение площади
фигуры F увеличивается ( уменьшается) во столько раз, во
сколько новая единица меньше (дольше) старой.
5. Если фигура F1 является частью фигуры F2 ,то численное
значение площади фигуры F1 не больше численного значения
площади фигуры F2 , т.е. F1 ⊂ F2 ⇒ S(F1)≤S(F2)
7.
ЗАДАЧА №1.Найдите площадь столешницы, длина
которой равна 10дм, а ширина – 5см.
b = 5см.
Решение.
S = a b.
10дм=100см.
Найти S.
S = 100 * 5 =500(см2).
Дано:
a = 10дм,
8.
ЗАДАЧА №2Длина школьного коридора равна 28м, а его
ширина в 4 раза меньше. Чему равна
площадь коридора?
Дано:
Решение.
a = 28м,
S = a b, b - ?
b – в 4 раза
меньше
Найти S.
b = 28 : 4 = 7(м).
S = 28 * 7 = 196(м2).
Ответ: 196м2.
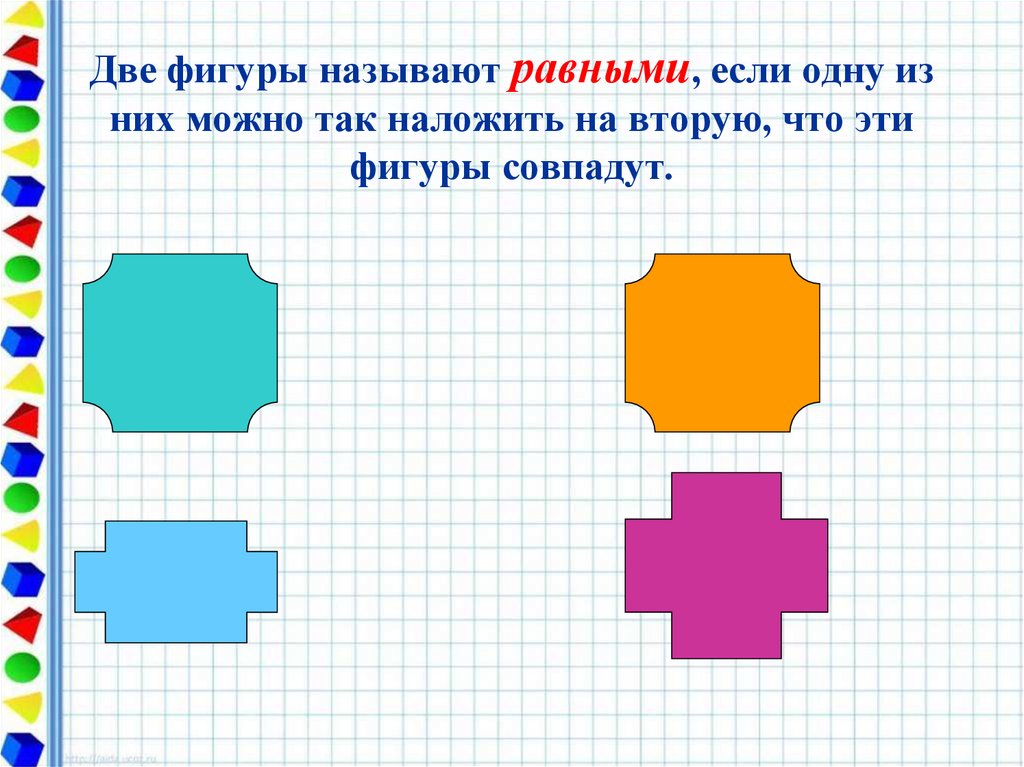
9. Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.
10.
ND
А
L
C
K
M
Многоугольники называются
равносоставленными, если их можно разбить на
соответственно равные части. S = S1 + S2
B
11.
ЗАДАЧА №3Равны ли площади?
12cм
6см
3см
Две фигуры, имеющие равные площади,
называются равновеликими.
12. Работа в классе
№1028№1032
№1036
13. Вопросы для самоконтроля
Что такое площадь?
Перечислите свойства площади?
Какие фигуры называют равными?
Какие фигуры называют равновеликими?
Какие фигуры называют равносоставленными?
Зачем нужна палетка?
Да
• Равносоставленные фигуры всегда равновелики?
• Равновеликие фигуры всегда равносоставленные?
• Любые два равновеликих многоугольника всегда
равносоставлены?
• Могут ли 2 равносоставленных треугольника иметь
разные площади?
Нет
Да
Да
14. Домашнее задание
№1027(3)№1037












 mathematics
mathematics








