Similar presentations:
Занимательная геометрия . Начальные сведения. 7 класс
1.
Занимательная геометрия . Начальныесведения.
2.
Да, путь познания не гладок.Но знаем мы со школьных лет:
Загадок больше, чем разгадок,
И поискам предела нет!
Л. Татьяничева.
3.
Цель:Существенно расширить
геометрические представления детей
Помочь освоить в процессе
практической деятельности
основные геометрические фигуры, их
свойства, способы построения
Формировать умения изображать
простейшие геометрические фигуры
и композиции из них на бумаге и в
форме чертежа
Формирование умения выполнять,
читать и преобразовывать чертеж.
4.
Для первобытных людей важную роль играла формаокружающих предметов.
По форме и цвету они отличали съедобные грибы от
несъедобных, пригодные для построек породы деревьев, от
тех, которые годятся только на дрова, вкусные орехи от
горьких и ядовитых…
Овладевая окружающим миром, люди знакомились с
простейшими геометрическими фигурами.
Специальных названий для них, конечно, еще не было.
Говорили: « такой же, как кокосовый орех» или:
« такой же как соль».
А когда люди стали строить дома из дерева, пришлось
глубже разобраться, какую форму придавать стенам и
крыше… Люди научились вытесывать из древесных
стволов прямоугольные балки. И сами того не зная,
занимались геометрией.
Геометрией занимались женщины, изготавливая одежду,
охотники, изготавливая наконечники для копий и стрел или
бумеранги особо сложной формы, рыболовы, делая такие
крючки из кости, чтобы рыба с них не сорвалась.
Форма тел рассматривалась тогда отдельно от их
свойств.
5.
До нас дошли обломки древней глиняной посуды, покоторым можно видеть, как лучше и лучше овладевал
человек геометрическими формами.
И вот настал день, когда был изготовлен гончарный
круг: посуде придавалась округлая форма.
Изобрели каток: от дерева отрезали кусок с почти
одинаковой толщиной в начале и конце. Тяжелые грузы
перетаскивались с помощью таких бревен (цилиндров).
Так появилось колесо.
Издавна люди украшали себя, одежду, жилище. Многие,
созданные давным-давно украшения, имели ту или иную
геометрическую форму: бусинки были шарообразны,
кольца и браслеты имели форму окружности…
Древние мастера научились придавать красивую форму
бронзе и золоту, серебру и драгоценным камням.
А художники, расписывая дворцы, находили все новые
геометрические формы.
Процесс знакомства с различными видами
геометрических фигур сменился новым этапом –
знакомством с их свойствами.
6.
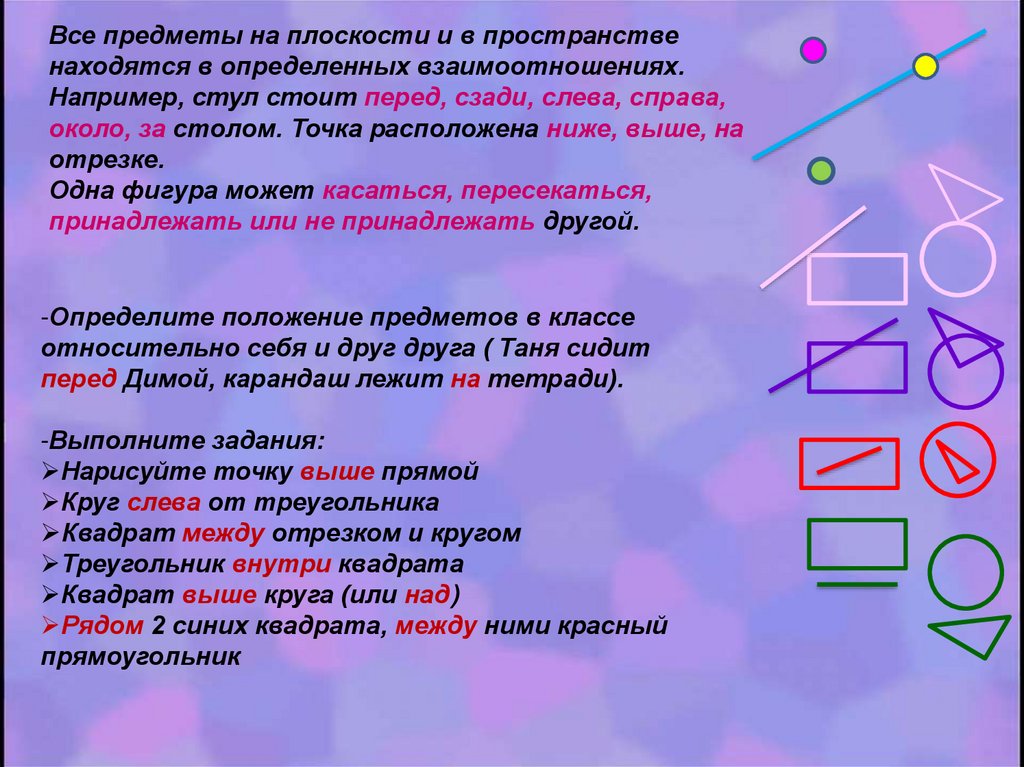
Все предметы на плоскости и в пространственаходятся в определенных взаимоотношениях.
Например, стул стоит перед, сзади, слева, справа,
около, за столом. Точка расположена ниже, выше, на
отрезке.
Одна фигура может касаться, пересекаться,
принадлежать или не принадлежать другой.
-Определите положение предметов в классе
относительно себя и друг друга ( Таня сидит
перед Димой, карандаш лежит на тетради).
-Выполните задания:
Нарисуйте точку выше прямой
Круг слева от треугольника
Квадрат между отрезком и кругом
Треугольник внутри квадрата
Квадрат выше круга (или над)
Рядом 2 синих квадрата, между ними красный
прямоугольник
7.
«Точка, точка, двакрючочка,
В стране ГЕ МЕТРИЯ
Носик, ротик, оборотик...
Вот
обормотик»
жилаи– вышел…
была маленькая
красная точка
.
Однажды ей стало скучно, и она отправилась на
--С помощью каких геометрических
поиски себе подружек. По дороге она встретила
фигур и их элементов изображен
,человечек?
потом
и
и еще много других.
И стало их так много, что выстроились они в один
ряд плечом к плечу и получилась линия.
Когда точки идут прямо, получается прямая линия,
когда неровно, криво – кривая:
8.
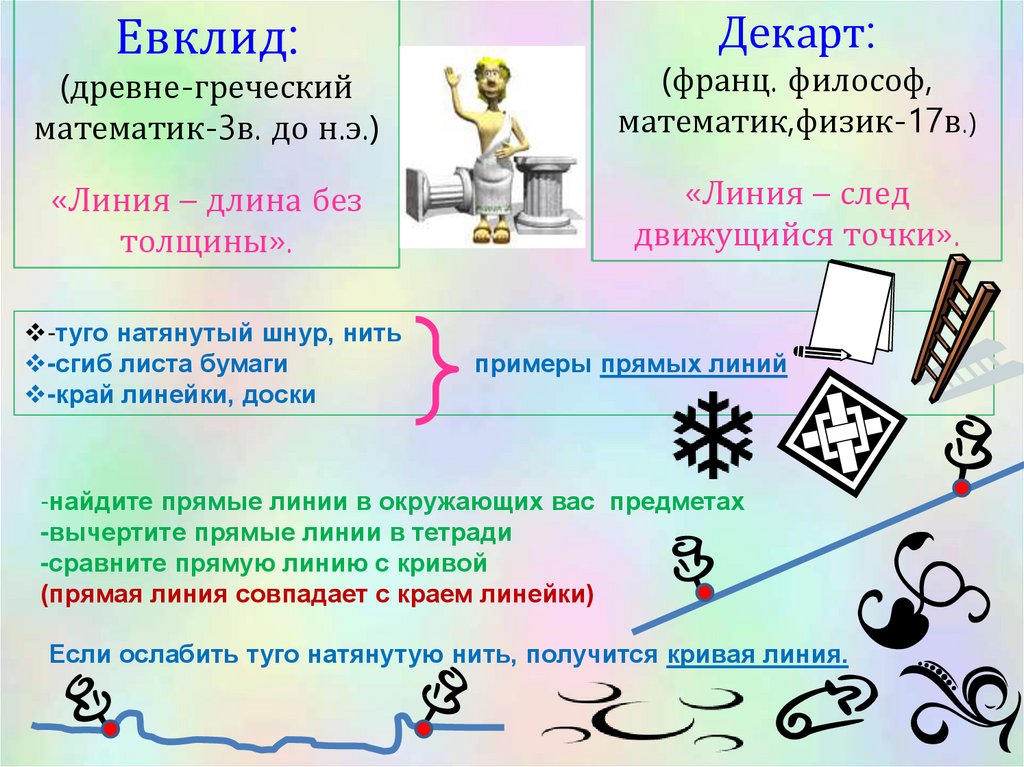
Евклид:Декарт:
(древне-греческий
математик-3в. до н.э.)
(франц. философ,
математик,физик-17в.)
«Линия – длина без
толщины».
«Линия – след
движущийся точки».
-туго натянутый шнур, нить
-сгиб листа бумаги
-край линейки, доски
примеры прямых линий
-найдите прямые линии в окружающих вас предметах
-вычертите прямые линии в тетради
-сравните прямую линию с кривой
(прямая линия совпадает с краем линейки)
Если ослабить туго натянутую нить, получится кривая линия.
9.
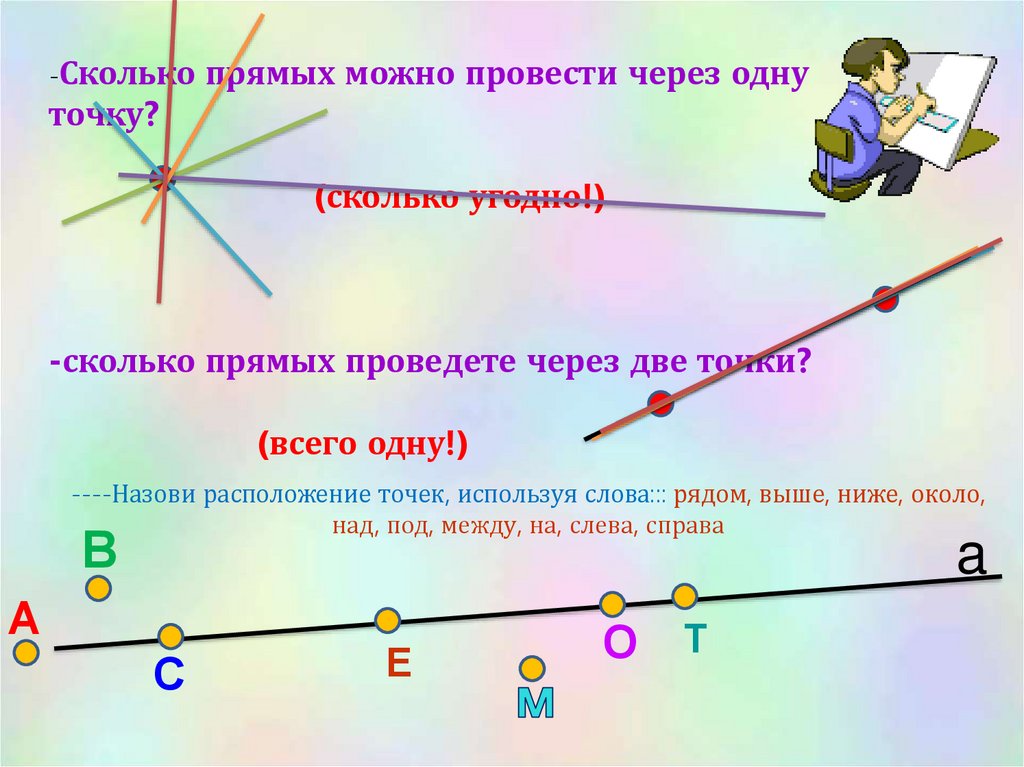
-Сколькопрямых можно провести через одну
точку?
(сколько угодно!)
-сколько прямых проведете через две точки?
(всего одну!)
----Назови расположение точек, используя слова::: рядом, выше, ниже, около,
над, под, между, на, слева, справа
В
a
А
С
Е
О Т
10.
Жил – былОднажды
. Был он очень любознательный и хотел все знать.
вышел Карандаш на Прямую линию.
Долго он шел по ней. Устал и говорит: «Когда же конец пути?»
-Эй, ты, Карандаш! –засмеялась прямая. Разве ты не знаешь, что у прямой
нет конца?
-Тогда я поверну назад. Я, наверное, пошел не в ту сторону.
- У прямой совсем нет концов- сказала Прямая и спела про себя песенку:
«Без конца и края линия прямая.
Хоть сто лет по ней иди,
Не найдешь конца пути».
Опечалился Карандаш. А Прямая продолжила:
-Ну, если ты не хочешь идти без конца, то отметь на прямой две точки.
-Ура! Появились два конца! Теперь я могу гулять по прямой от одной
точки до другой! Что же это получилось?
- Это ОТРЕЗОК – улыбнулась Прямая.
11.
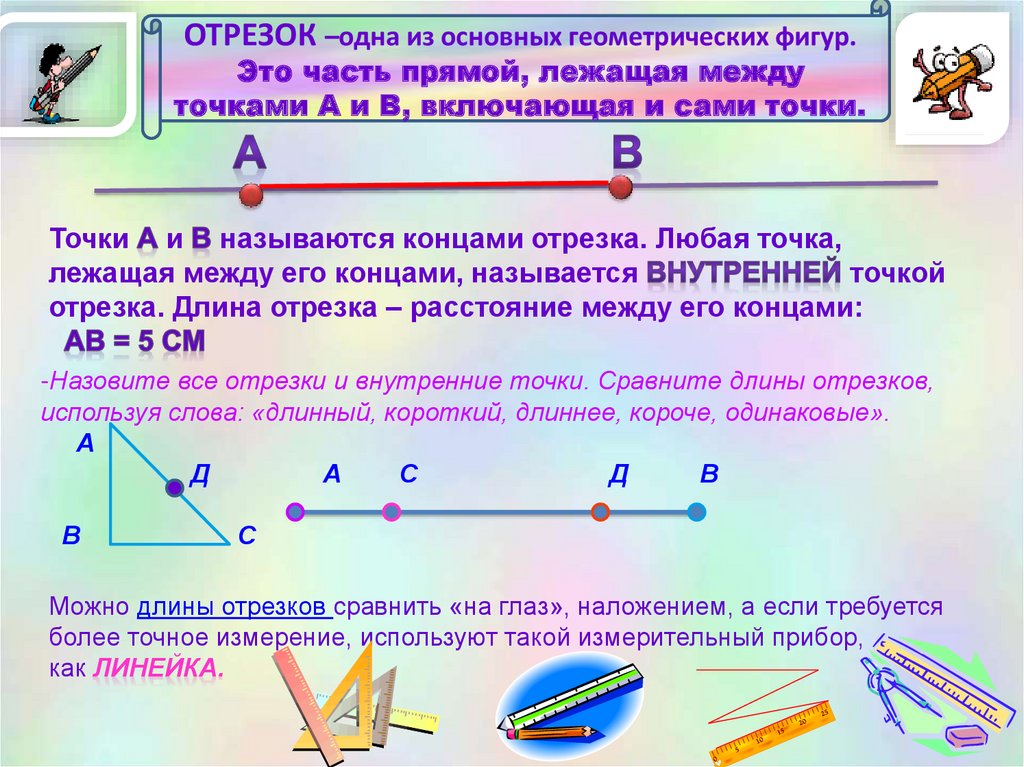
ОТРЕЗОК –одна из основных геометрических фигур.Это часть прямой, лежащая между
точками А и В, включающая и сами точки.
Точки и называются концами отрезка. Любая точка,
лежащая между его концами, называется
точкой
отрезка. Длина отрезка – расстояние между его концами:
-Назовите все отрезки и внутренние точки. Сравните длины отрезков,
используя слова: «длинный, короткий, длиннее, короче, одинаковые».
А
Д
А
С
Д
В
В
С
Можно длины отрезков сравнить «на глаз», наложением, а если требуется
более точное измерение, используют такой измерительный прибор,
как ЛИНЕЙКА.
12.
Однаждыкоторому он гулял.
Взял он с собой
решил отнять у Прямой ее отрезок, по
и потихоньку вырезал отрезок.
Соединил оставшиеся концы и завязал.
Только не понятно, что же это такое на Прямой получилась?
А получилось на прямой два ЛУЧА, выходящие из одной точки. Один
то конец у них есть, а второго нет!
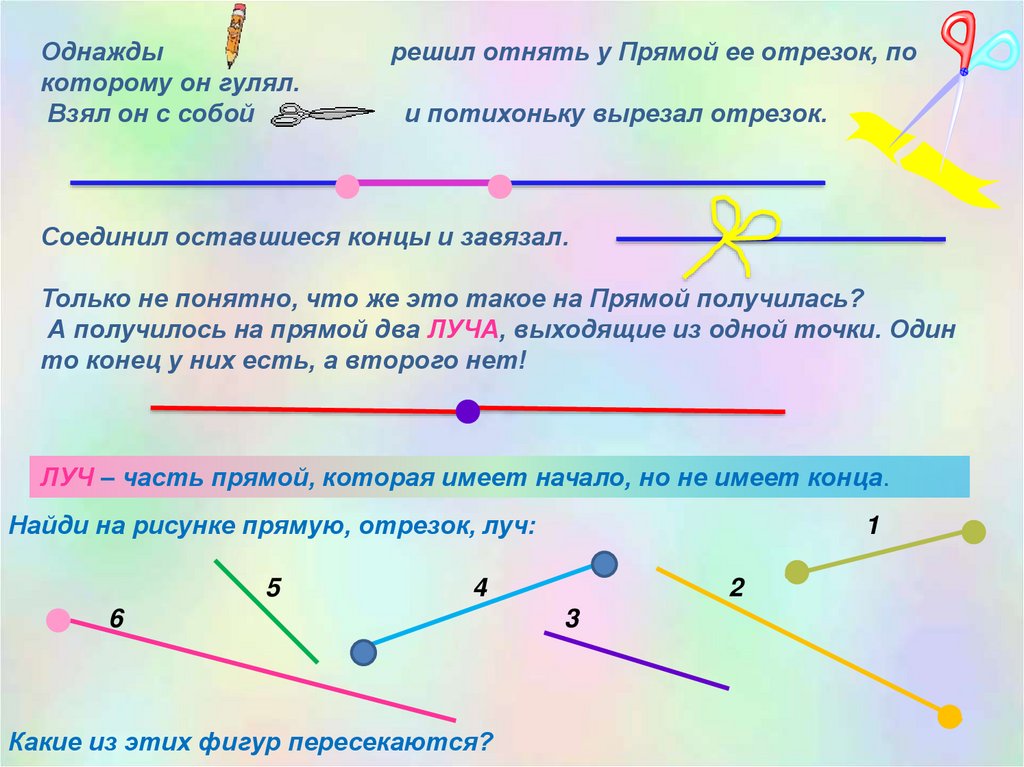
ЛУЧ – часть прямой, которая имеет начало, но не имеет конца.
Найди на рисунке прямую, отрезок, луч:
5
1
4
6
Какие из этих фигур пересекаются?
2
3
13.
Ножницы разрезали прямую на 2 луча. Циркуль подтянулэти лучи, соединил их концами, и вот что получили:
-Да, это не прямая,- воскликнула Точка. – Тут прямо не
проедешь, надо поворачивать. Что же это получилось?
- Это УГОЛ – сказал Циркуль.
- То место, где соединяются лучи – ВЕРШИНА, а сами лучи,
идущие от вершины – СТОРОНЫ.
Катается Точка по углу, как по горке и приговаривает:
От вершины по лучу, словно с горки покачу.
Только луч теперь – « она»:
Он зовется «сторона».
-Нельзя ли горку круче сделать? – попросила Точка.
Циркуль сдвинул стороны угла вот так:
-Какой острый угол! – запищала Точка. С такой горки кубарем
покатишься!
- А кому нужны эти углы?- воскликнула Точка.
- Архитектору. Он чертит дом на бумаге, а потом по этому чертежу и
строят дом.
- Ой, как много углов! Но мне кажется, что они
все одинаковые.
-Да, они все одинаковые и называются
ПРЯМЫМИ.
14.
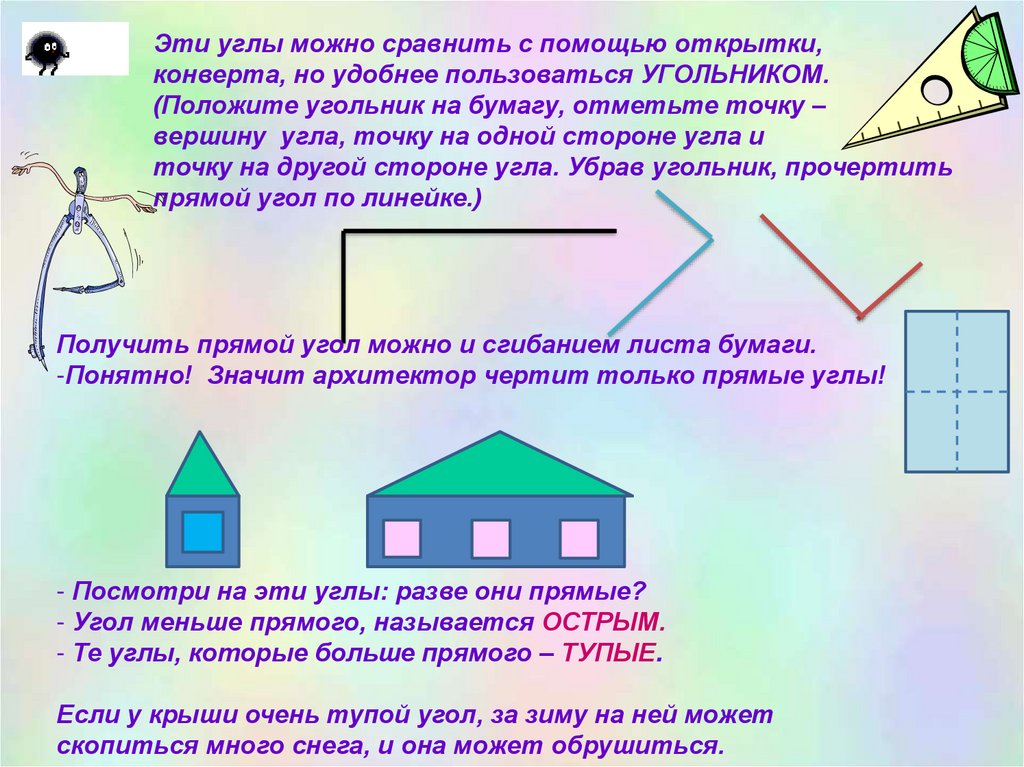
Эти углы можно сравнить с помощью открытки,конверта, но удобнее пользоваться УГОЛЬНИКОМ.
(Положите угольник на бумагу, отметьте точку –
вершину угла, точку на одной стороне угла и
точку на другой стороне угла. Убрав угольник, прочертить
прямой угол по линейке.)
Получить прямой угол можно и сгибанием листа бумаги.
-Понятно! Значит архитектор чертит только прямые углы!
- Посмотри на эти углы: разве они прямые?
- Угол меньше прямого, называется ОСТРЫМ.
- Те углы, которые больше прямого – ТУПЫЕ.
Если у крыши очень тупой угол, за зиму на ней может
скопиться много снега, и она может обрушиться.
15.
- Какой из этих углов прямой, какой меньше прямого, какой больше?- Нарисуйте такой же рисунок, отметьте одним цветом острые
углы, другим – тупые.
- Какой угол образуют стрелки на часах, показывая разное время?
- На этом рисунке 6 углов. Найди их.
16.
Отправились Точкас Циркулем
в путь. Циркуль впереди
идет,
широко шагает, быстро, ноги у него длинные. А маленькая Точка ножками
семенит, еле за ним поспевает. Вдруг им преградило путь огромное
чернильное пятно. Ни обойти его, ни перепрыгнуть.
Вспомнили они про своих друзей – отрезки. А они уже тут как тут!
Перекинулся один отрезок на ближний островок, другой пробежал по нему
до конца, зацепился за конец и – хлоп! – перекинулся на следующий. Третий
отрезок побежал по первым двум, за ним 4-ый, 5-ый… Хлоп – хлоп – хлоп! –
и мост готов.
Посадил Циркуль точку себе на плечо и перенес ее по мостику на другую
сторону.
-Какая интересная линия получилась! – воскликнула Точка.
- Это - ЛОМАНАЯ – объяснил Циркуль.
ЛОМАНАЯ – линия, состоящая из 2-х или более отрезков, расположенных
так, что конец 1-ого отрезка служит началом 2-ого и т. д.
Элементы ломаной: отрезки (звенья ), вершины, углы.
Ее длину можно найти, вычислив сумму ее звеньев ( отрезков).
17.
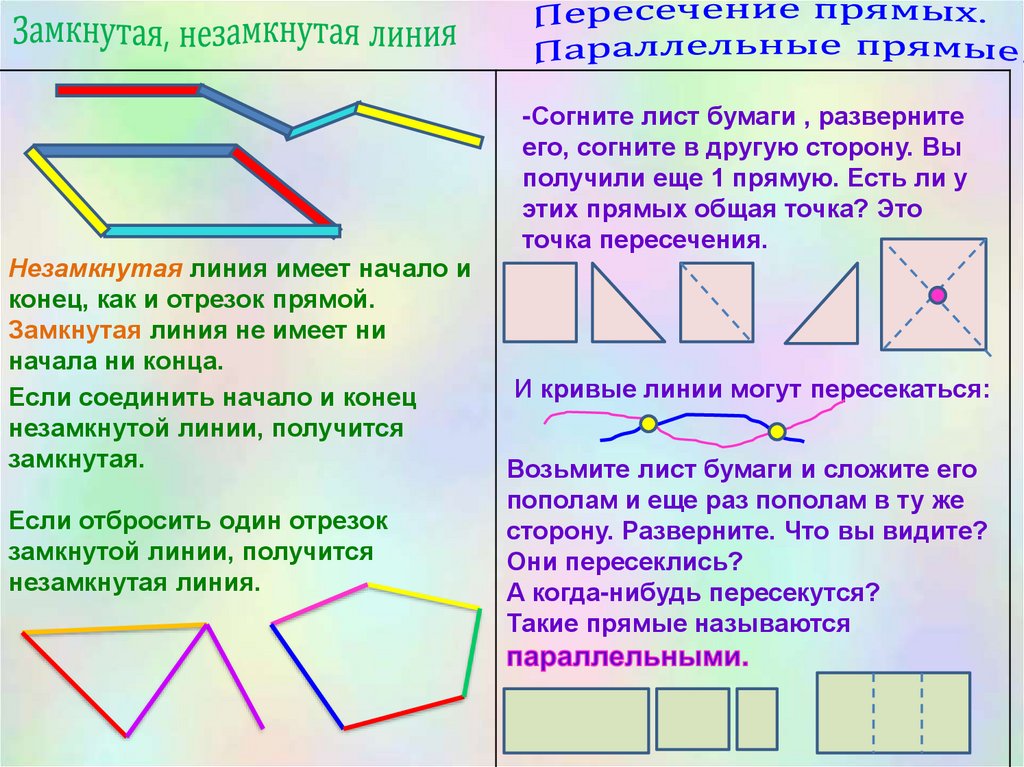
-Согните лист бумаги , развернитеего, согните в другую сторону. Вы
получили еще 1 прямую. Есть ли у
этих прямых общая точка? Это
точка пересечения.
Незамкнутая линия имеет начало и
конец, как и отрезок прямой.
Замкнутая линия не имеет ни
начала ни конца.
Если соединить начало и конец
незамкнутой линии, получится
замкнутая.
Если отбросить один отрезок
замкнутой линии, получится
незамкнутая линия.
И кривые линии могут пересекаться:
Возьмите лист бумаги и сложите его
пополам и еще раз пополам в ту же
сторону. Разверните. Что вы видите?
Они пересеклись?
А когда-нибудь пересекутся?
Такие прямые называются
18.
19.
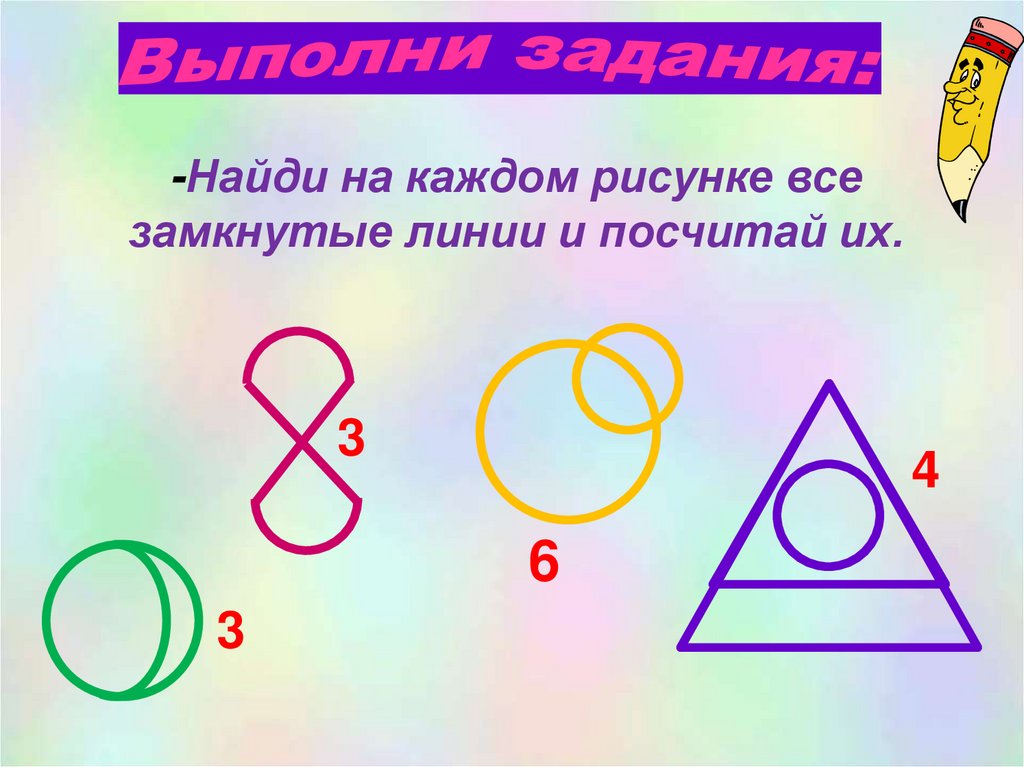
-Найди на каждом рисунке всезамкнутые линии и посчитай их.
3
4
6
3
20.
21.
Сколько лучей исходит из отмеченной точки? Сколькопрямых проходит через эту точку?
Сколько лучей на каждом чертеже? Отрезков?
Сколько на каждом чертеже прямых, лучей, отрезков?
22.
Циркуль позвал 3 отрезка и они соединилисьвот так:
-Что это такое? – спросил Циркуль.
- Это же ломаная линия! – воскликнула Точка.
- А сколько в ней отрезков (звеньев)?
- А углов? Это и есть ТРЕУГОЛЬНИК. Отрезки
в нем называются сторонами, а вершины
углов – вершинами треугольника.
Точка и Циркуль оказались в Городе Треугольников, где
все было треугольным: и дома, и деревья, и человечки,
которые пели песенку:
« Ты на меня, ты на него
На всех нас посмотри.
У нас всего, у нас всего
У нас всего по три.
Три стороны и три угла
И столько же вершин
И трижды трудные дела
Мы трижды совершим.
Мы в нашем городе – друзья,
Дружнее – не сыскать.
Мы – треугольников семья,
Нас каждый должен знать!»
23.
Привет!У меня 4 угла, 4 вершины, 4
стороны.
Вы узнали меня?
Четырехугольник, у
которого все углы
прямые, а
противоположные
стороны равны…
ПРЯМОУГОЛЬНИК
Он давно знакомый мой.
Каждый угол в нем прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
Как зовут его?
Что общего у ПРЯМОУГОЛЬНИКА и
?
Поиграем?
Мышонок взял 4 одинаковые палочки и захотел сложить
квадрат, но у него получилась вот такая фигура:
Можно ли ее назвать квадратом?
Почему? Что общего у него с квадратом?
Чем отличается?
(Это РОМБ)
А что можно сказать про РОМБ с прямыми углами?
24.
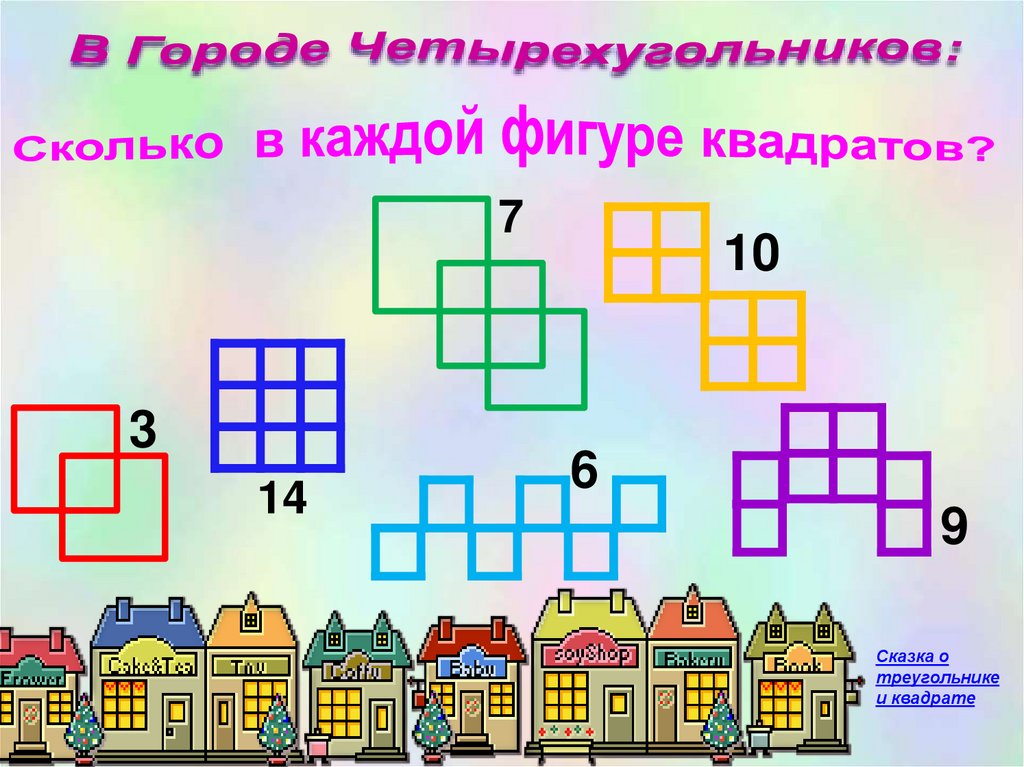
73
14
10
6
9
Сказка о
треугольнике
и квадрате
25.
Попросила под Новый Год Снегурочка Мышонканарисовать ей Снеговика. Долго трудился Мышонок: не
выходит: то круги неровные получаются, то одинаковые.
А Снеговика из снежных шаров лепят, значит, на бумаге
должны быть ровные круги, да еще – нижний – самый
большой, средний – поменьше, а верхний – самый
маленький.
Вспомнил Мышонок, кто может помочь ему!
А вот и сам он на встречу идет.
- Только чтобы круги разные получились, я должен
отмерить по линейке РАДИУС для каждого круга!
-А что еще это такое?
- Когда я черчу на бумаге круг, от моей иголочки
остается след – маленькая точка. Это ЦЕНТР КРУГА.
У круга есть одна подруга,
знакома всем ее наружность!
она идет по краю круга
и называется – ОКРУЖНОСТЬ
А РАДИУС – это отрезок, который соединяет ЦЕНТР
КРУГА с любой точкой ОКРУЖНОСТИ,
Чем больше этот отрезок ( РАДИУС), тем больше круг
или окружность!
ДИАМЕТР – отрезок, соединяющий 2 точки окружности и
проходящий через ее центр ( равен 2-м радиусам).
26.
Где круг, а гдеокружность?
27.
Точка и Карандаш летели на.
По пути их самолет потерпел аварию: треснуло
треугольное крыло. И они вынуждены были сесть в
Городе Четырехугольников. Все отправились на
завод, и по дороге заметили, что все предметы
здесь: и дома, и деревья, и человечки имели форму
четырехугольников.
Здесь были улицы Прямоугольников и Ромбов,
а вот улицы Квадратов не было. Почему?
На заводе было очень много крыльев, но все они
были четырехугольные.
И тогда на помощь позвали Ножницы.
-Надо разрезать четырехугольники по ДИАГОНАЛИ, и
получится 2 треугольника – сказали Ножницы. Они
провели линию, соединяющую противоположные
вершины четырехугольника и такой же линией
соединили другие противоположные вершины, т.е.
получилось две ДИАГОНАЛИ.
-Потом четырехугольник разрезали
-по одной из линий, и получили
-треугольное крыло,
-которым заменили поломанное.
28.
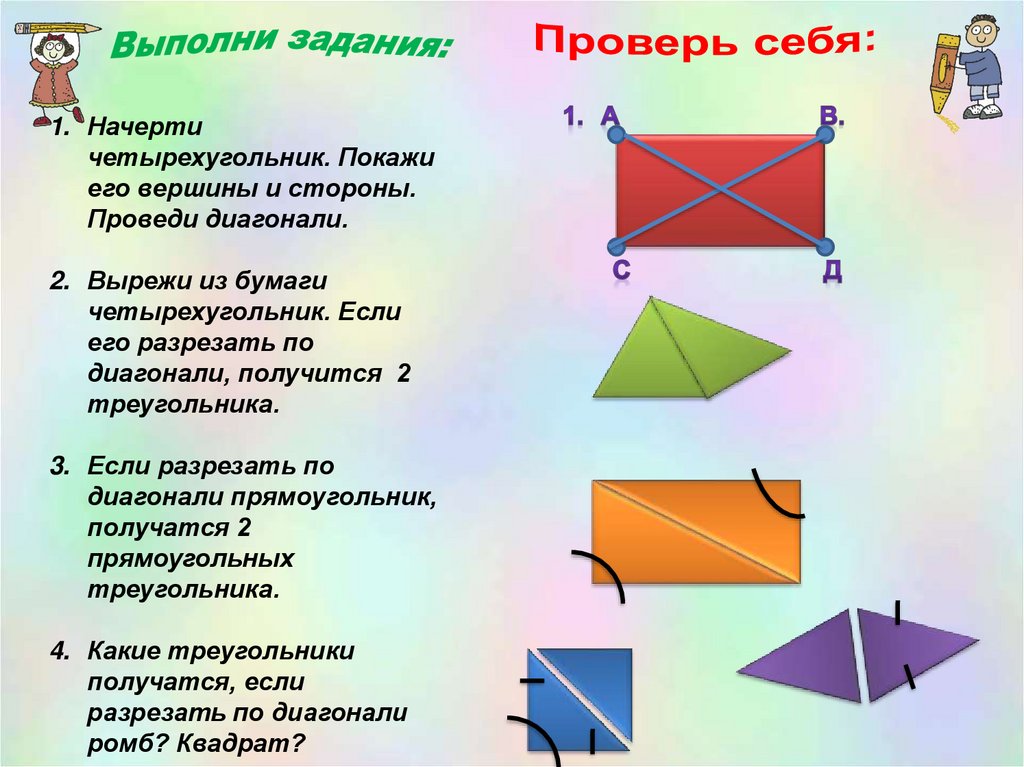
1. Начертичетырехугольник. Покажи
его вершины и стороны.
Проведи диагонали.
2. Вырежи из бумаги
четырехугольник. Если
его разрезать по
диагонали, получится 2
треугольника.
3. Если разрезать по
диагонали прямоугольник,
получатся 2
прямоугольных
треугольника.
4. Какие треугольники
получатся, если
разрезать по диагонали
ромб? Квадрат?
29.
1. Вырежи из бумаги 2 равныхпрямоугольных треугольника.
Сложи их так, чтобы получился
прямоугольник.
2. Вырежи из бумаги 2 равных
равнобедренных треугольника.
Сложи их так, чтобы получился
ромб.
3. Какие треугольники нужно
сложить, чтобы получился
квадрат?
4. Про всякий квадрат можно
сказать, что он – прямоугольник.
Можно ли наоборот?
5. Про всякий квадрат можно
сказать, что он – ромб. А
наоборот?
6. Вот ромбы.
Сколько здесь квадратов?
Прямоугольные,
равнобедренные
Нет: у квадрата все углы
прямые и все стороны равны
Нет: у квадрата все углы
прямые
30.
Цилиндрпараллелепипед
КВАДРАТ
ПРЯМОУГОЛЬНИК
Плоские фигуры полностью лежат на поверхности
стола, доски, т.е. целиком принадлежат плоскости.
КаждуюКРУГ
такую фигуру можно вырезать из листа
Куб
шар
пирамида
бумаги.
Геометрические тела не принадлежат целиком
плоскости.
ТРЕУГОЛЬНИК
конус
31.
Найди в рисунках знакомые тебе геометрическиетела:
(Куб, цилиндр, шар, конус, пирамида,
параллелепипед).


























 mathematics
mathematics








