Similar presentations:
Теория вероятностей и математическая статистика
1.
ТЕОРИЯ ВЕРОЯТНОСТЕЙИ МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
ЗФО, направления 220400, 220700
4 семестр
Лектор: канд. физ.-мат. наук, доцент
Смирнова Людмила Алексеевна
2. Лекция 1. Тема: Предмет и основные понятия теории вероятностей
Теория вероятностей, подобно другимразделам математики, развилась из
потребностей практики: в абстрактной
форме она отражает закономерности,
присущие случайным явлениям
массового характера.
3.
Эти закономерности играют важнуюроль в физике и других областях
естествознания, технических
дисциплинах, экономике,
социологии, биологии.
В связи с бурным развитием
массового производства продукции,
результаты теории вероятностей стали
использоваться для контроля
изготовленной продукции и
организации процесса производства.
4. Предметом теории вероятностей является изучение закономерностей массовых однородных случайных явлений.
5.
ОСНОВНЫЕ ПОНЯТИЯТЕОРИИ ВЕРОЯТНОСТЕЙ
6. Опыт (эксперимент)
- состоитв наблюдении за
объектами или явлениями, в
строго определенных условиях
и измерении значений какихлибо признаков этих объектов
(явлений).
7. ПРИМЕРЫ ЭКСПЕРИМЕНТОВ
бросание игрального кубика,
стрельба по мишени,
сдача экзамена,
проверка качества изделия,
химический эксперимент,
и т.п.
8. СТАТИСТИЧЕСКИЙ ЭКСПЕРИМЕНТ
Эксперимент называютСТАТИСТИЧЕСКИМ, если он
может быть повторен в
практически неизменных
условиях неограниченное
число раз.
9.
СОБЫТИЕСОБЫТИЕМ называется
явление, которое происходит
в результате осуществления
определенных действий при
заданных условиях.
ПРИМЕР. Бросаем шестигранный
игральный кубик. События:
- выпало четное число очков;
- выпало число очков, кратное 3;
- выпало более 5 очков.
10. СЛУЧАЙНОЕ СОБЫТИЕ
СЛУЧАЙНЫМ называют событие,которое может произойти или не
произойти в результате некоторого
опыта.
Обозначают заглавными буквами
А, В, С, D,… (латинского
алфавита).
11.
Рассмотрим нескольконаиболее популярных
в теории вероятностей
экспериментов.
12. Опыт 1:
Подбрасывание монеты.Испытание – подбрасывание
монеты; события – монета
упала «орлом» или «решкой».
«решка» - лицевая сторона «орел» - обратная сторона
монеты (реверс)
монеты (аверс)
13. Опыт 2:
Подбрасывание кубика.Испытание –
подбрасывание кубика;
события – выпало 1, 2, 3, 4, 5
или 6 очков.
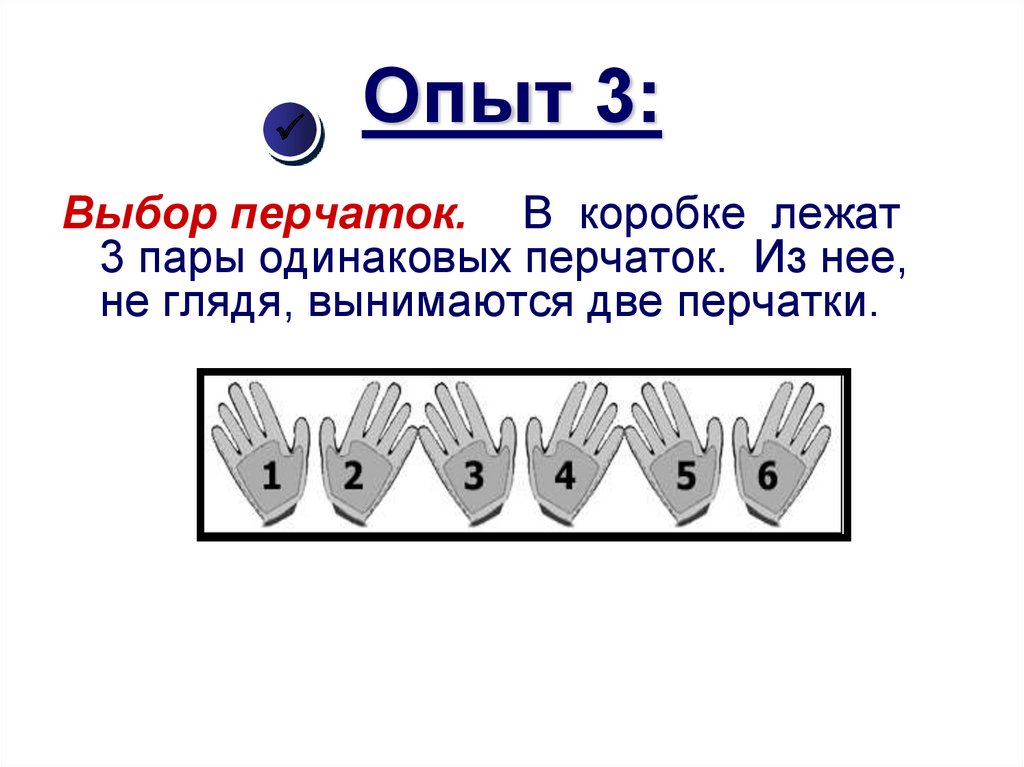
14. Опыт 3:
Выбор перчаток. В коробке лежат3 пары одинаковых перчаток. Из нее,
не глядя, вынимаются две перчатки.
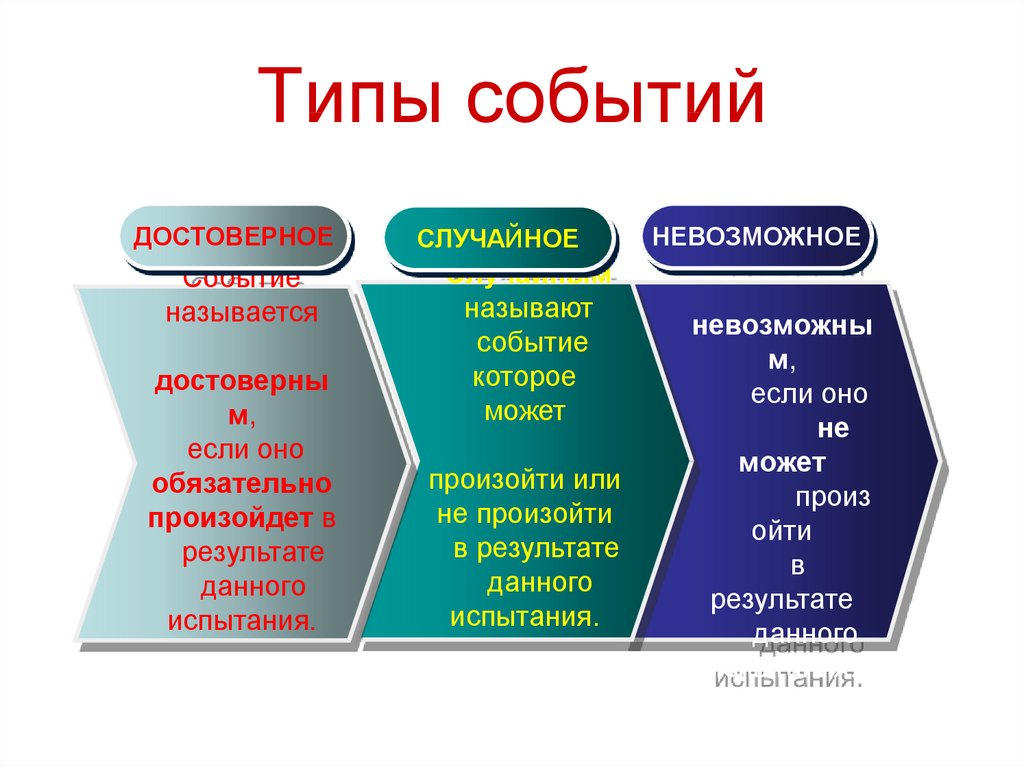
15. Типы событий
ДОСТОВЕРНОЕСобытие
называется
достоверны
м,
если оно
обязательно
произойдет в
результате
данного
испытания.
СЛУЧАЙНОЕ
Случайным
называют
событие
которое
может
произойти или
не произойти
в результате
данного
испытания.
Событие
называется
НЕВОЗМОЖНОЕ
невозможны
м,
если оно
не
может
произ
ойти
в
результате
данного
испытания.
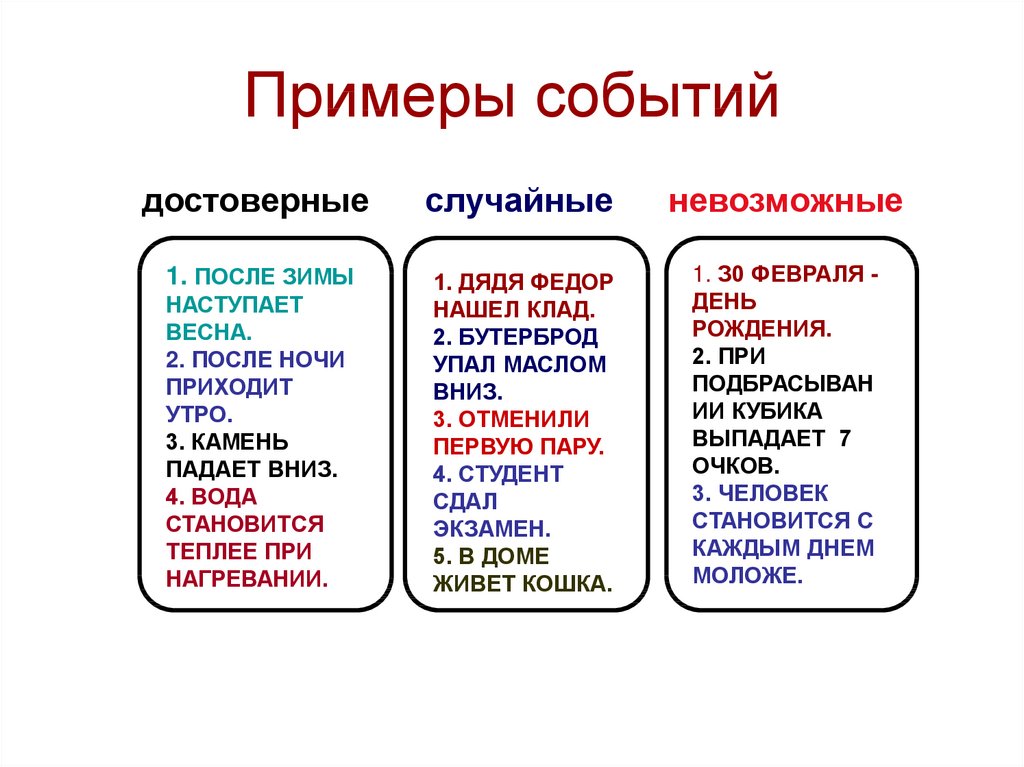
16. Примеры событий
достоверныеслучайные
невозможные
1. ПОСЛЕ ЗИМЫ
1. ДЯДЯ ФЕДОР
НАШЕЛ КЛАД.
2. БУТЕРБРОД
УПАЛ МАСЛОМ
ВНИЗ.
3. ОТМЕНИЛИ
ПЕРВУЮ ПАРУ.
4. СТУДЕНТ
СДАЛ
ЭКЗАМЕН.
5. В ДОМЕ
ЖИВЕТ КОШКА.
1. З0 ФЕВРАЛЯ ДЕНЬ
РОЖДЕНИЯ.
2. ПРИ
ПОДБРАСЫВАН
ИИ КУБИКА
ВЫПАДАЕТ 7
ОЧКОВ.
3. ЧЕЛОВЕК
СТАНОВИТСЯ С
КАЖДЫМ ДНЕМ
МОЛОЖЕ.
НАСТУПАЕТ
ВЕСНА.
2. ПОСЛЕ НОЧИ
ПРИХОДИТ
УТРО.
3. КАМЕНЬ
ПАДАЕТ ВНИЗ.
4. ВОДА
СТАНОВИТСЯ
ТЕПЛЕЕ ПРИ
НАГРЕВАНИИ.
17.
Задание 1В мешке лежат 10 елочных шаров: 3 синих,
3 белых и 4 красных.
Охарактеризуйте события как достоверные,
невозможные или случайные.
События:
а) из мешка вынули 4 шара и они все синие;
б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они
оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не
оказалось шара зеленого цвета.
18. ИСХОД
ИСХОДОМ (или элементарнымисходом, элементарным
событием) называется один из
взаимоисключающих друг друга
вариантов событий, которым
может завершиться данный
эксперимент.
19. Число возможных исходов в каждом из рассмотренных выше опытах.
Опыт 1. Подбрасывание монеты– 2 исхода: «орел», «решка».
Опыт 2. Подбрасывание кубика
– 6 исходов: 1, 2, 3, 4, 5, 6.
Опыт
3.
Выбор
наугад
одной
из
3-х
пар
перчаток – 3 исхода: «обе перчатки на
левую руку», «обе перчатки на правую
руку», «перчатки на разные руки».
20.
Задание 2Запишите множество исходов для
следующих испытаний.
а) В урне четыре шара с номерами два,
три, пять, восемь. Из урны наугад
извлекают один шар.
б) В копилке лежат три монеты
достоинством в 1 рубль, 2 рубля и 5
рублей. Из копилки достают две монеты.
в) Монету подбрасывают трижды.
21. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Перестановкой из n различныхэлементов называется любой
упорядоченный набор этих элементов.
Число различных перестановок из n
элементов равно
Pn n! 1 2 3 ... n
Пример. Сколько четырехзначных чисел с
разными цифрами можно составить из
цифр {1,2,3,4}? P4 4! 1 2 3 4 24
22. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Размещением из n элементов по mназывается любой упорядоченный
набор из m различных элементов,
выбранных из общей совокупности в
n элементов.
n!
m
Число размещений равно Аn
(n m)!
Пример. Имеется 5 различных сигнальных
морских флагов. Сколько сообщений,
составленных из 3-х флагов, можно
5!
1 2 3 4 5
3
передать?
А
60
5
(5 3)!
2!
23. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Сочетанием из n элементов по mназывается любой неупорядоченный
набор из m различных элементов,
взятых из совокупности в n элементов.
n
!
m
Число сочетаний равно Cn
m!(n m)!
Пример. Сколькими способами можно
из коробки с 10 разноцветными
карандашами наугад извлечь три
карандаша?
10! 1 2 3 4 5 6 7 8 9 10 720
C
120
3! 7!
1 2 3 7!
6
3
10
24. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ
Вероятностью события А называетсяотношение числа исходов опыта,
благоприятствующих появлению события,
к общему числу равновозможных исходов
опыта.
m
Формула: P A
n
где n – число всех равновозможных исходов,
m – число исходов, благоприятных для
появления события А.
25. .
Задание3
Технический контроль проверяет из партии в 50
деталей 10 деталей, взятых наудачу. Партия
содержит 5 нестандартных деталей. Какова
вероятность того, что среди проверяемых
деталей попадется 1 нестандартная?
Решение. Событие А – среди отобранных 10
деталей попалась 1 нестандартная деталь.
10
n С50 - число способов выбора 10 деталей из 50;
9
m С45
С51 - число способов выбора 9 деталей из
45 стандартных и 1 детали из 5 нестандартных.
9
С45
С51
Р А
0,43.
10
С50























 mathematics
mathematics








