Similar presentations:
Построение таблиц истинности для логических выражений
1.
Тема урока:«Построение таблиц истинности для
логических выражений»
Цель: Формирование навыков применения технологии
построения таблиц истинности для составных логических
выражений.
2. Построение таблицы истинности
Таблица истинности – это таблица, показывающаяистинность сложного высказывания при всех возможных
значениях входящих переменных.
Последовательность действий:
1. Определить количество строк в таблице:
• количество строк = 2n+1,
где n – количество
логических переменных, 1 – строка заголовков
2. Определить количество столбцов в таблице:
• количество столбцов = количеству логических
переменных + количество логических операций
3. Расставить приоритеты действий:
• приоритеты: ( ), ¬, &, V, импликация, эквиваленция;
4. Заполнить столбцы входных переменных наборами
значений.
5. Заполнить таблицу истинности, выполняя логические
операции в соответствии с приоритетами действий.
3. В составных высказываниях логические операции выполняются в следующем порядке:
1.2.
3.
4.
5.
6.
В составных высказываниях логические
операции выполняются в следующем
порядке:
Действия в скобках
Отрицание (не)
Конъюнкция (и)
Дизъюнкция (или)
Импликация
Эквиваленция
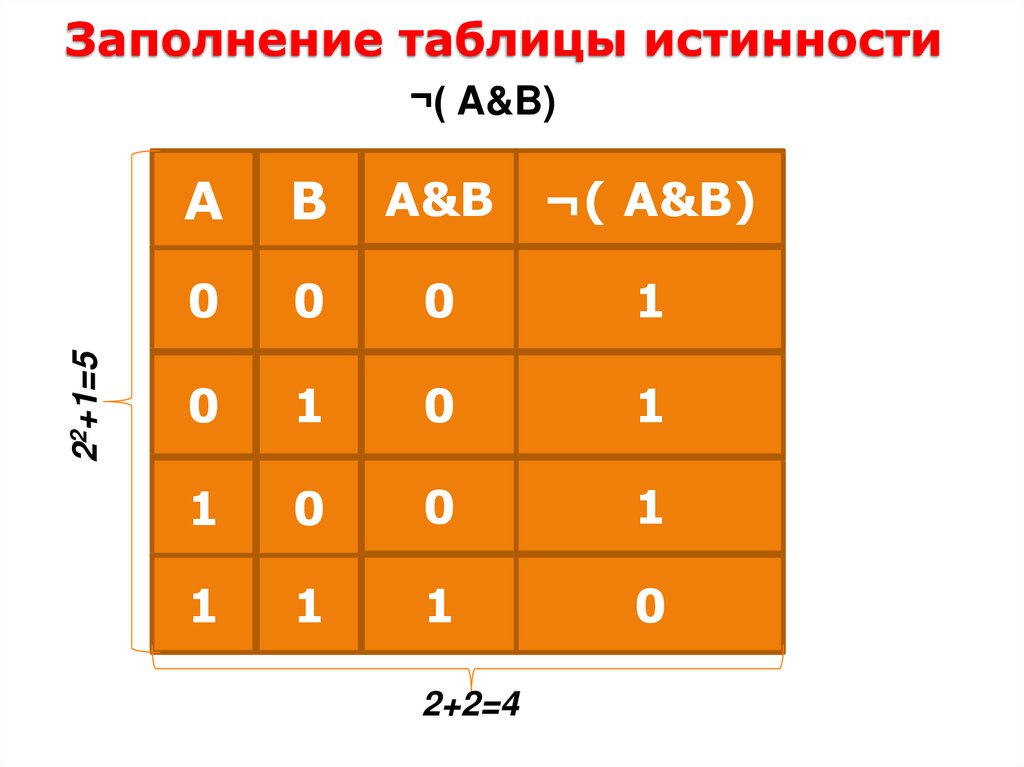
4. Заполнение таблицы истинности
22+1=5¬( A&B)
A
B
A&B
¬( A&B)
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
2+2=4
5.
Наборы входных переменных, во избежание ошибок,рекомендуют вводить следующим образом:
1) разделить столбец значений первой переменной
пополам и заполнить верхнюю часть колонки нулями, а
нижнюю — единицами;
2) разделить столбец значений второй переменной на
четыре части и заполнить четверти чередующимися
группами нулей и единиц, начиная с группы нулей;
3) продолжать деление столбцов значений последующих
переменных на 8, 16 и т. д. частей и заполнение их
группами нулей или единиц до тех пор, пока группа нулей
(единиц) не будет состоять из одного символа.
6. например:
Построить таблицу истинности для выражения:F=(A
А
В
0
0
0
А
В
B)&(A
B)
А
В
А
В
0
1
1
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
F
7. РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ
Логические выражения, у которыхтаблицы истинности совпадают,
называют равносильными.
8. Доказать, что логические выражения: А & В и А В, равносильны
Доказать, что логические выражения:А & В и А В, равносильны
Таблица истинности для А&В
Таблица истинности для А v В
А
В
А
В
А & В
А
В
А
В
А
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
1
1
0
Таблицы истинности совпадают, следовательно, логические
выражения равносильны.
В
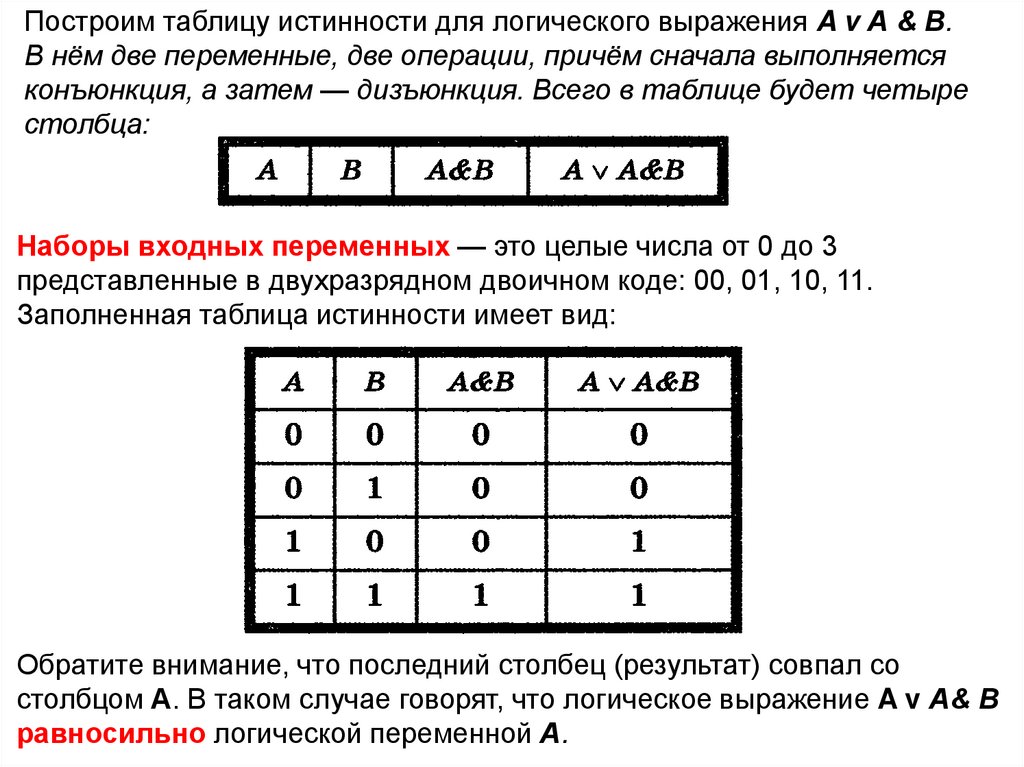
9.
Построим таблицу истинности для логического выражения A v А & В.В нём две переменные, две операции, причём сначала выполняется
конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре
столбца:
Наборы входных переменных — это целые числа от 0 до 3
представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со
столбцом А. В таком случае говорят, что логическое выражение A v А& В
равносильно логической переменной А.
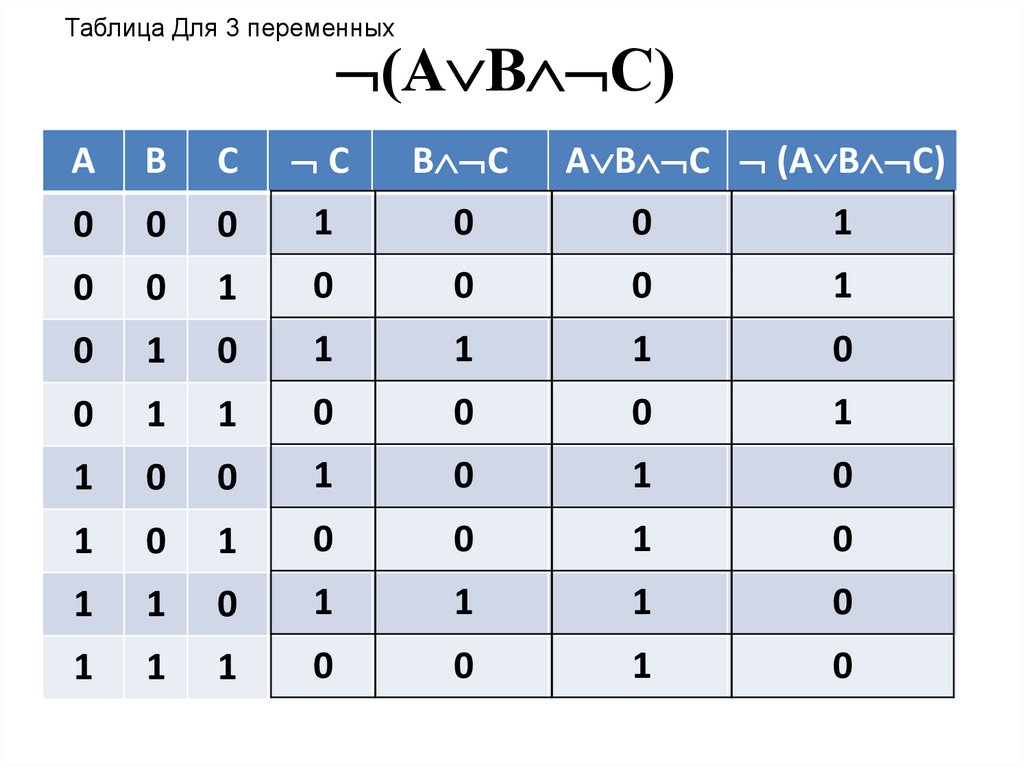
10.
Таблица Для 3 переменных(А В С)
А
В
С
С
В С
А В С (А В С)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
1
0
1
1
1
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
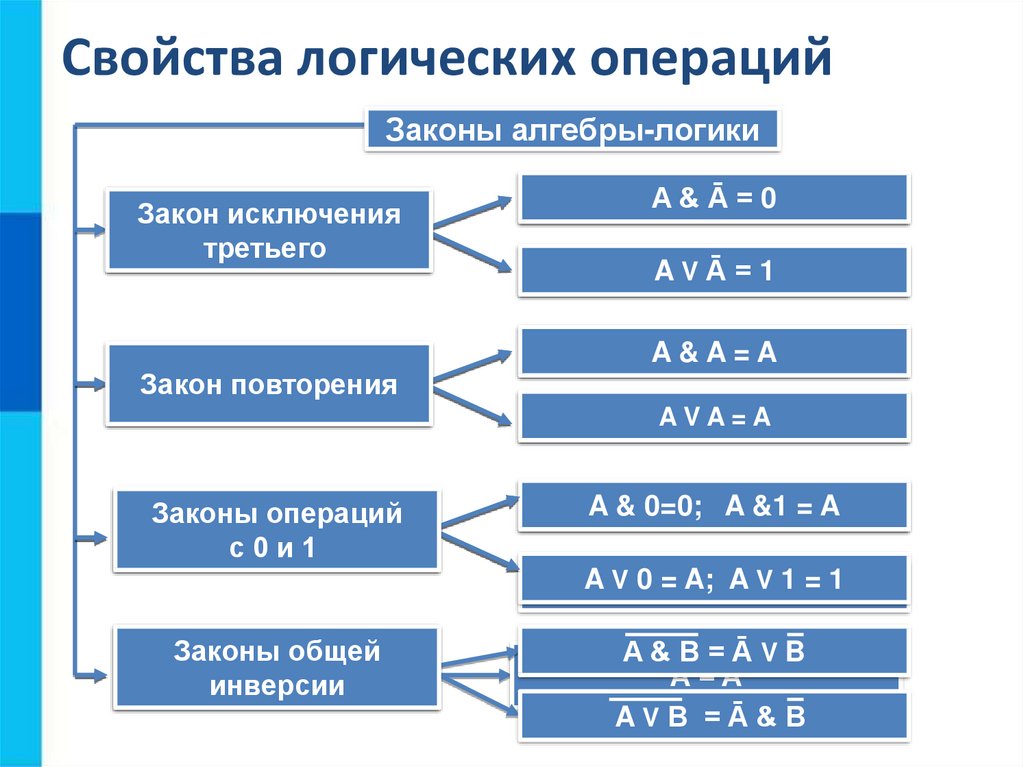
11.
Свойства логических операцийЗаконы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B







 mathematics
mathematics








