Эки эселенген бурчтун тригонометриялык функциялары
1.
АЛГЕБРА САБАГЫАраван району
Салижан Шарипов атындагы орто мектеп
Өзбек тилинде
Тема: Эки эселенген бурчтун
тригонометриялык функциялары
2.
Алгебра9-синф
Мурабдуллаев Исломжон
Математика мугалими
3.
4. Иккиланган бурчакнинг синуси
Қўшиш формуласининг синусидан фойдаланамиз:sin(α + β) = sinα cosβ + cosα sinβ
β ни α алмаштирсак:
sin(α + α) = sinα cos α + sinα cosα
Иккиланган бурчакнинг синуси формуласини оламиз.
sin 2 2 sin cos
5. Иккиланган бурчакнинг косинуси
Қўшиш формуласининг косинусидан фойдаланамиз:cos(α + β) = cosα cosβ − sinα sinβ
β ни α алмаштирсак:
cos(α + α) = cosα cos α − sinα sinα
Иккиланган бурчакнинг косинуси формуласини оламиз.
cos 2 cos sin
2
2
6. Иккиланган бурчакнинг косинусини бошқа формуласи
Иккиланган бурчакнинг косинуси формуласидан фойдаланамиз:cos 2 cos 2 sin 2
cos2α = 1 − sin2α
сos2α ни алмаштирамиз:
натийжада:
cos 2α = 1 − sin2α − sin2α = 1 − 2sin2α
cos 2α = 1 − 2sin2α
7. Иккиланган бурчакнинг косинусининг бошқа формуласи
Иккиланган бурчакнинг косинусидан фойдаланамизcos 2 cos 2 sin 2
sin2α = 1 − cos 2α
sin2α ни алмаштирамиз:
натийжада:
cos 2α = cos 2α − 1 + cos 2α
cos 2α = 2cos 2α − 1
8. Полезные равенства:
cos 2α = 1 − 2sin2αу ҳолда
2sin2α = 1 − cos 2α
cos 2α = 2cos 2α − 1
2cos 2α = 1 + cos 2α
у ҳолда
9.
Иккиланган бурчакнинг тангенсиҚўшиш формуласининг тангенсидан фойдаланамиз, β ни α га
алмаштирамиз, натийжада иккиланган бурчакнинг тангенси келиб чиқади.
tg tg
tg ( )
1 tg tg
tg tg
tg ( )
1 tg tg
Иккиланган бурчакнинг тангенсининг формуласи.
2tg
tg 2
1 tg 2
10.
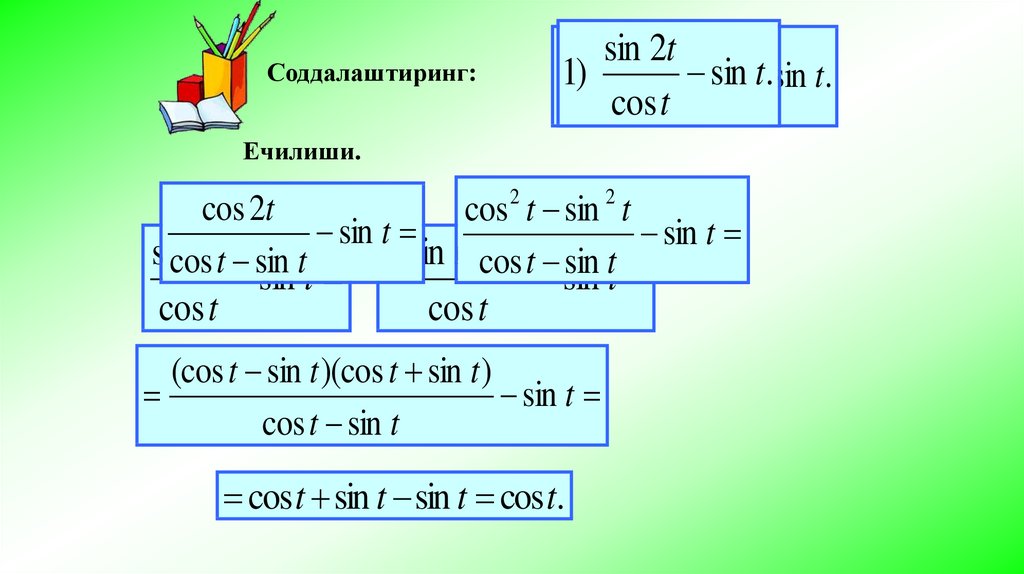
Соддалаштиринг:sincos
2t 2t
sin t.sin t.
21)
costt sin t
cos
Ечилиши.
cos 2t
cos 2 t sin 2 t
sin t
sin t
sincos2tt sin t
2 sin t cos
tt sin t
cos
sin t
sin t
cos t
cos t
(cos t sin t )(cos t sin t )
sin tt.
2 sin t sin t sin
cos t sin t
cos t sin t sin t cos t.
11.
sincos40
36 sin 18
. 0
21))
.
0
sin 20cos18
00
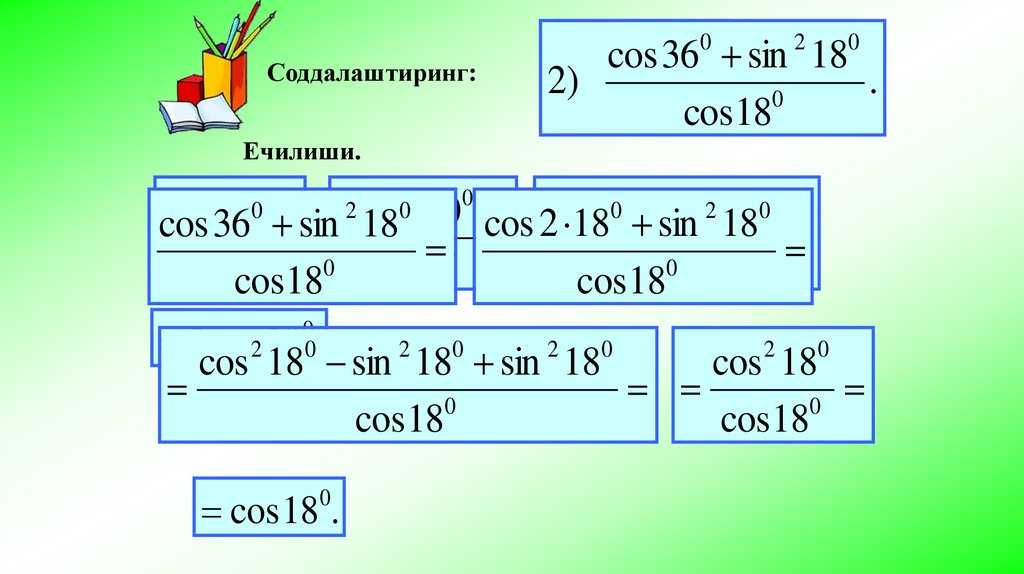
Соддалаштиринг:
2
0
Ечилиши.
sin 36
40 sinsin182 20 cos 22 sin
20
cos18
20
18
sin
cos
0
0
0
0
sin 20cos180 sin 20
sin
20
cos18
0
0
2
0
0
0
0
2
0
0
2 cos2 20 .
2
0
2
0
2
0
cos 18 sin 18 sin 18
cos 18
0
0
cos18
cos18
0
0
cos 18 .
0
12.
Ҳисобланг:2 sin 15 cos15 sin 30
0
cos15
0
0
0 2
sin 15
0
Жавоб: 0,5
cos 15 2 sin 15 cos15 sin 15
2
1 sin 30
2
0
Жавоб: 1,5
13.
Ҳисобланг:2 sin cos sin
8
8
4
Жавоб:
2/2
2
cos sin
2
8
8
2
2 2
2
cos
2 sin cos sin
2
8
8
8
8
2
1 sin
2
4
Жавоб: − 1
14.
Тригонометриянингформулалари
15.
Қўшишнинг формулалари1) sin( ) sin cos cos sin
2 ) sin( ) sin cos cos sin
3) cos( ) cos cos sin sin
4 ) cos( ) cos cos sin sin
tg tg
5)tg( )
1 tg tg
tg tg
6 )tg( )
1 tg tg
Асосий тригонометрик формулалар
sin 2 cos 2 1 откуда
sin 2 1 cos 2 ;
2
2
cos
1
sin
.
sin
cos
tg
ctg
cos
sin
tg ctg 1
1
1 ctg
sin 2
1
2
tg 1
cos 2
2
Иккиланган бурчакнинг тригонометрик
функциялари
sin 2 2 sin cos
cos 2 cos 2 sin 2
2tg
tg 2
1 tg 2
2 sin 2 1 cos 2
2 cos2 1 cos 2
cos 2 1 2 sin 2
cos 2 2 cos 2 1














 mathematics
mathematics