Лекция 25. Пролог. Решение логических задач

1. Лекция 25. Пролог. Решение логических задач.

Языки и методы
программирования.
Ст. преп. М.А. Сокольская

2. План.

1.
Логические задачи
a)
b)
2
Ханойские башни
Задача о расстановке ферзей

3. Пример 1. Ханойские башни.

Постановка задачи:
В игре используется три стержня и набор из N дисков
разного размера. Изначально все диски нанизаны
на левый стержень в порядке убывания диаметра.
Цель – переместить все диски на правый стержень,
используя центральный как запасной. Условия:
1.
Перемещать за один раз можно только один диск
(верхний)
2.
Нельзя класть диск на диск меньшего диаметра.
3

4. Стратегия решения

1.
2.
Один диск перемещается
непосредственно
N дисков переносятся в 3 этапа:
1.
2.
3.
4
Перенести N-1 дисков на средний стержень
Перенести последний диск на правый
стержень
Перенести N-1 дисков со среднего стержня на
правый.

5. Используемые предикаты

1.
2.
3.
5
Предикат hanoy (integer), показывающий со
сколькими дисками идет игра.
Предикат move, описывающий перенос N
дисков с левого стержня на правый с
промежуточным средним.
Предикат inform, указывающий на действие
с конкретным диском, вспомогательный для
вывода пояснений.

6.

6
Domains
loc = right; middle, left
Predicates
hanoy (integer)
move (integer, loc, loc, loc)
inform (loc, loc)
Clauses
hanoy(N) :- move (N, left, middle, right).
move (1, A, _ , C) :- inform (A, C), !.

7.

7
move (N, A, B, C) :- M=N-1, move (M, A, C, B), inform
(A, C), move (M, B, A, C).
inform (Loc1, Loc2) :- nl, write (“Move a disk from ”,
Loc1, “ to ”, Loc2).
Goal
hanoy (3)
Результат:
Move a disk from left to right
Move a disk from left to middle
Move a disk from right to middle
Move a disk from left to right

8.

Move a disk from middle to left
Move a disk from middle to right
Move a disk from left to right
yes
8

9. Пример 2. Задача о ферзях

9
Постановка задачи:
Расставить на шахматной доске 8х8 восемь шахматных
ферзей так, чтобы ни один из них угрожал другому.
Построим модель.
Перенумеруем ряды клеток, расположенных по
горизонтали и вертикали от 1 до 8. Для нумерации
диагоналей поделим их на два типа:
Diagonal=8+Column-Row (тип 1)
Diagonal=Row+Column-1 (тип 2)
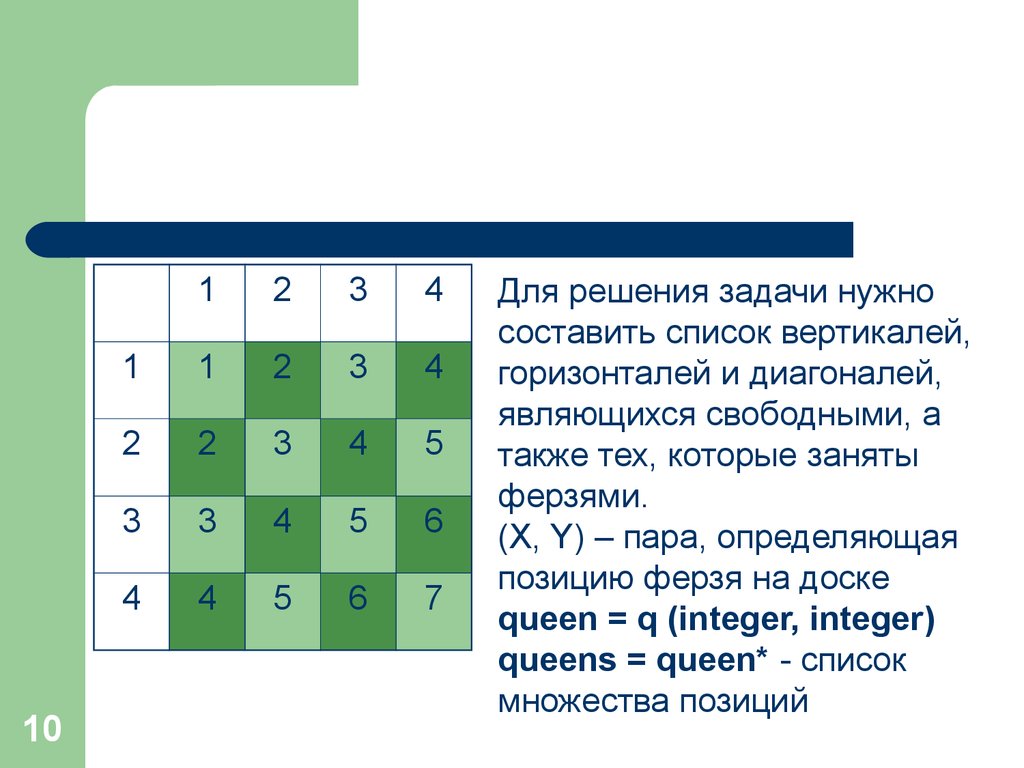
Для примера перенумеруем клетки квадрата 4х4

10.

10
1
2
3
4
1
1
2
3
4
2
2
3
4
5
3
3
4
5
6
4
4
5
6
7
Для решения задачи нужно
составить список вертикалей,
горизонталей и диагоналей,
являющихся свободными, а
также тех, которые заняты
ферзями.
(X, Y) – пара, определяющая
позицию ферзя на доске
queen = q (integer, integer)
queens = queen* - список
множества позиций

11.

11
freelist = integer* - списки свободных вертикалей,
горизонталей и диагоналей.
Шахматную доску опишем как единый объект:
board = board (queens, freelist, freelist, freelist,
freelist)
Для примера:
пустая доска 4х4:
board ([], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4, 5, 6, 7], [1, 2, 3,
4, 5, 6, 7])
доска с одним ферзем:
board ([1, 1], [2, 3, 4], [2, 3, 4], [2, 3, 4, 5, 6, 7], [2, 3, 4, 5,
6, 7])

12.

12
Ферзи размещаются по одному до тех пор, пока не
будут заняты все вертикали, горизонтали и
диагонали.
Введем предикат
placeN (integer, board, board), для которого опишем
правила.
Списки вертикалей и горизонталей пусты
placeN(_, board(D, [ ], [ ], X, Y), board(D, [ ], [ ], X, Y)) :-!.
Связь между двумя расстановками при добавлении
ферзя:
placeN (N, Board1, Result) :- place_a_queen(N, Board1,
Board2), placeN (N, Board2, Result).

13.

13
place_a_queen (integer, board, board)
Нового ферзя добавляем к списку стоящих на доске
ферзей.
Среди свободных горизонталей ищем ту, на которую
можно поставить нового ферзя и удалить ее из
списка свободных горизонталей.
findandremove (R, Rows, NewR)
Аналогично действуем для вертикалей с переменной С.
С помощью R и C вычислим диагонали и будем
искать их в списках свободных диагоналей.

14. Листинг программы

14
domains
queen = q (integer, integer)
queens = queen*
freelist = integer*
board = board (queens, freelist, freelist, freelist, freelist)
predicates
placeN (integer, board, board)
place_a_queen (integer, board, board)
nqueens (integer)
makelist (integer, freelist)
findandremove (integer, freelist, freelist)
nextrow (integer, freelist, freelist)

15.

15
clauses
nqueens (N) :- makelist (N, L), Diagonal=N*2-1,
makelist
(Diagonal, LL), placeN (N, board([], L, L, LL, LL), Final), write
(Final).
placeN(_, board(D, [], [], D1, D2), board(D, [], [], D1, D2)) :-!.
placeN (N, Board1, Result) :- place_a_queen(N, Board1, Board2),
placeN (N, Board2, Result).
place_a_queen (N, board(Queens, Rows, Columns, Diag1, Diag2),
board([q(R, C)|Queens], NewR, NewC, NewD1, NewD2)) :nextrow (R, Rows, NewR),
findandremove (C, Columns, NewC),
D1=N+C-R, findandremove (D1, Diag1, NewD1),
D2=R+C-1, findandremove (D2, Diag2, NewD2).

16.

16
findandremove (X, [X | Rest], Rest).
findandremove (X, [Y | Rest], [Y | Tail]) :findandremove (X, Rest, Tail).
makelist (1, [1]).
makelist (N, [N | Rest]) :- N1=N-1, makelist (N1,
Rest).
nextrow (Row, [Row | Rest], Rest).
goal
nqueens(5), nl, readchar (_).

17. Итоги

Мы рассмотрели:
Примеры использования списков
1.
2.
3.
17
Поиск пути в графе (см. лекцию 24).
Задачу о Ханойских башнях
Задачу расстановки ферзей.