Решение неравенств с одной переменной

1. Решение неравенств с одной переменной

2.

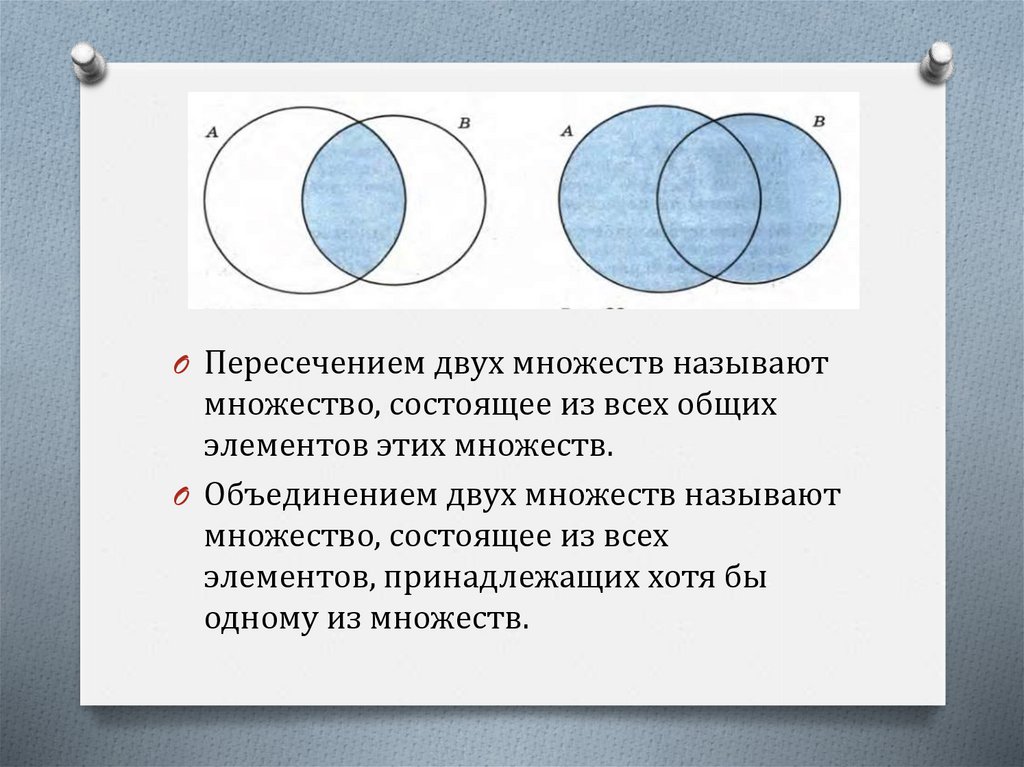
O Пересечением двух множеств называют
множество, состоящее из всех общих
элементов этих множеств.
O Объединением двух множеств называют
множество, состоящее из всех
элементов, принадлежащих хотя бы
одному из множеств.

3. Пусть А –множество натуральных делителей числа 12, а В –множество натуральных делителей числа 18.

O Обозначим буквой С – множество общих делителей
чисел 12 и 18, т.е. общих элементов множества А и В.
O Получим, что
Говорят, что
множество С является пересечением множеств А и В, и
пишут : А⋂В=С.

4. Пусть множество D – множество, которому принадлежат все элементы множества А и все элементы множества В.

O Говорят, что множество D является
объединением множеств А и В, и пишут :
O D=А⋃В

5. Устная работа

6.

O Неравенства, имеющие одни и те же
решения, называются равносильными.
O Неравенства, не имеющие решений, также
считаются равносильными.
O Например, неравенство 18 + 6х > 0
O равносильно неравенству 6х > -18,
O а это неравенство равносильно
неравенству х > -3.

7.

8.

9. Пример 1 : Решите неравенство

O 16х > 13х + 45
O Перенесём слагаемое 13х с противоположным
знаком в левую часть неравенства:
O 16х -13х > 45
O Приведём подобные слагаемые:
O 3х > 45
O Разделим обе части неравенства на
коэффициент, стоящий перед х:
O Х > 15.

10.

O Множество решений неравенства
состоит из всех чисел, больших 15. Это
множество представляет собой
открытый числовой луч (15;+ ∞).
O Ответ можно записать в виде числового
промежутка (15;+ ∞), или в виде
неравенства Х > 15, задающего этот
промежуток.

11. Пример 2: Решите неравенство

O 15х – 23 (х+1) > 2х + 11
O Раскроем скобки в левой части неравенства:
O 15х – 23х – 23 > 2х + 11
O Перенесём с противоположным знаком слагаемое 2х
из правой части неравенства в левую, а слагаемое -23
из левой части в правую и приведём подобные
слагаемые:
O 15х – 23х – 2х > 11+23
O -10 х > 34

12.

O Разделим обе части неравенства на коэффициент стоящий
перед х, при этом изменим знак неравенства на
противоположный,
O так как -10 < 0:
O Х < -3,4.
Множество решений данного неравенства представляет
собой открытый числовой луч (-∞; - 3,4).
Ответ: (-∞; - 3,4).