Similar presentations:
Лекция 35. Дифракция света
1. Лк-35
Дифракция света2.
Практическое использование интерференции света.Длина световых волн составляет доли микрона.
Непосредственно такие размеры не воспринимаются
органами чувств человека. Одна-ко полосы
интерференционных картин имеют макроскопические
размеры и позволяют сделать ощутимыми
микроскопические размеры световых волн и других
микроскопических деталей. Интерферометрия использует
интерференцию для измерений различных величин, таких
как размеры предметов, показатели преломления веществ,
угловые размеры звезд. Разрешающая способность
интерферометров, т.е. способность различить две близкие
по значению величины, может достигать сотых долей
длины используемой световой волны ≈10-8 м, что
недоступно для других типов измерителей.
3.
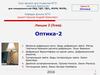
Интерферометр Физо. Используется для определенияплоскостности и чистоты обработки поверхности тел.
Картина – полосы равной толщины формируется в воздушном клине между измеряемым телом и эталонной
стеклянной пластинкой. Наличие на поверхности
тела мельчайших бугорков и
впадин приводит к искривлеНию интерференционных полос.
В качестве источника света
часто используется лазер.
В лаб. раб. «Кольца Ньютона»
использован интерферометр Физо.
4.
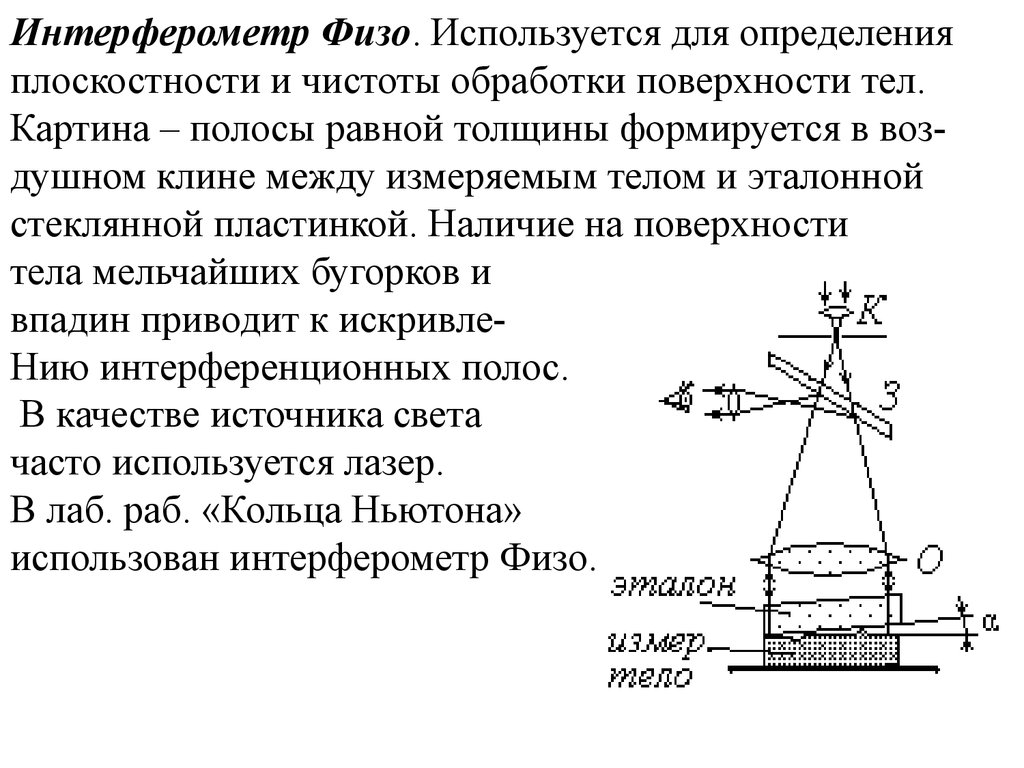
Интерферометр Майкельсона позволяет получитьинтерференцию лучей, отраженных от двух
пространственно разнесенных зеркал М1 и М2.
Перемещая или наклоняя одно из них можно получить
интерференционную картину «полосы
Равного наклона» или «полосы
равной толщины. В качестве одного из зеркал можно использовать исследуемую поверхность и
измерить ее неровность. Лазерные интерферометры Майкельсона позволяют проводить измерения при большой разности
хода, фиксируя относительные
величины расстояний до 10-8.
5.
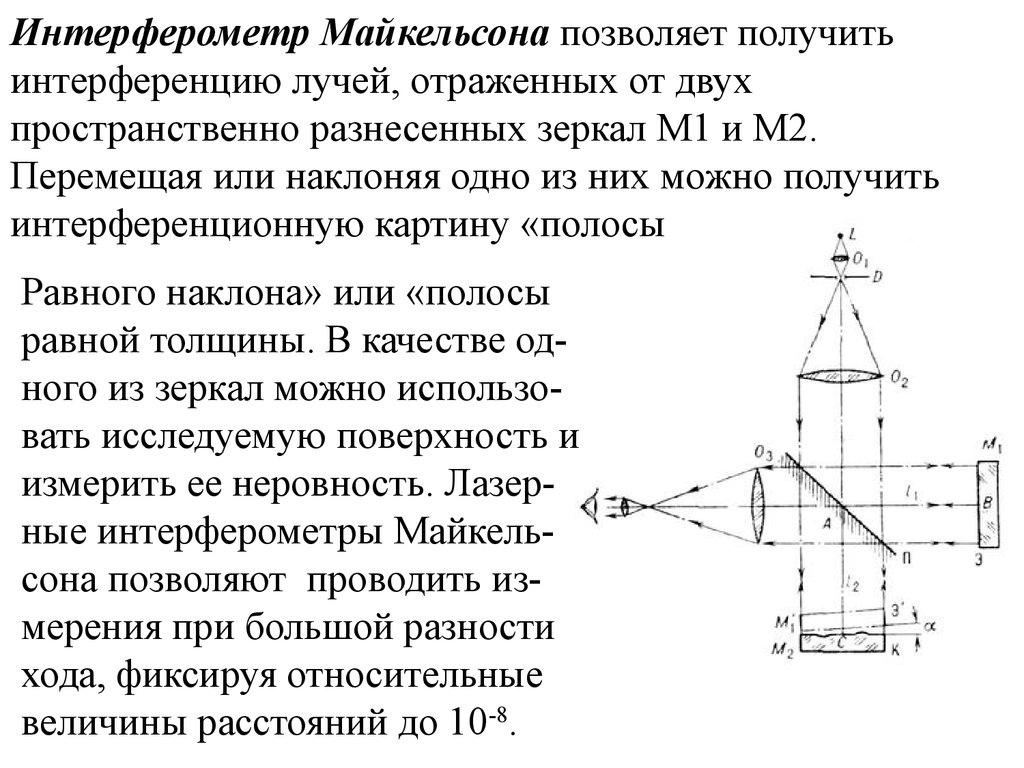
Интерферометр Жамена. Существуют двулучевые Интерферометры, предназначенные для измерения показателей преломления газов и жидкостей - интерференционныерефрактометры. Один из них - интерферометр Жамена.
Два луча, формируемые пластинкой Р1 из одного исходного,
проходят эталонное и исследуемое тела К1, К2. Затем оба
луча сводятся пластинкой Р2 в
окуляре и дают интерференционную картину «полосы равной
толщины». Малейшее изменение оптических свойств исследуемого тела приводит к сдвигу
полос картины
6.
Просветление оптики, так называется уменьшение отражения света от стеклянной поверхности. Дляэтого на поверхность оптического стекла наносят тонкую пленку с показателем преломления nп, меньшим,
чем а показатель преломления стекла nс . Необходимо получить интерференционный минимум для отраженных лучей 1 и 2. Условие минимума – разность
хода = λ/2. Для этого толщина пленки должна быть
равна h= λ/(4nп)
(35.1)
Для полного гашения отраженной волны необходимо выполнение условия .Осуществить просвет-ление для
всех волн видимого спект-ра
невозможно. Поэтому условие выполняют только для зеленого цвета.
7.
Создание высокоотражающих диэлектрических зеркал.Металлические зеркала имеют не очень хороший коэффициент отражения. До 10% света поглощается. Для получения коэффициента отражений, близкого к 1 создаются диэлектрические зеркала с многослойным отражающим слоем. На поверхность стекла наносятся множество прозрачных пленок из материалов с сильно отличающимися показателями преломления. В противоположность задаче
просветления здесь необходимо создать
интерференционный максимум для
отраженных от поверхностей раздела
лучей. Поэтому внешняя пленка имеет
максимальный коэффициент преломления. Удается получить зеркала с
коэффициентом отражения 0.99.
8.
Пятиминутка. Вычислить толщину просветляющейпленки и требуемый показатель преломления ее
материала, если ее необходимо нанести на
поверхность линзы, сделанной из стекла с
показателем преломления n=1.5.
9. ДИФРАКЦИЯ СВЕТА
10.
ДИФРАКЦИЯ СВЕТА.Дифракцией называется
огибание волнами препятствий, встречающихся на их
пути, или в более широком
смысле - отклонение
распространения волн вблизи
препятствий от законов
геометрической оптики.
Благодаря дифракции волны
могут попадать в область
геометрической тени, огибать
препятствия, проникать через
небольшие отверстия в
экранах и т. д..
11.
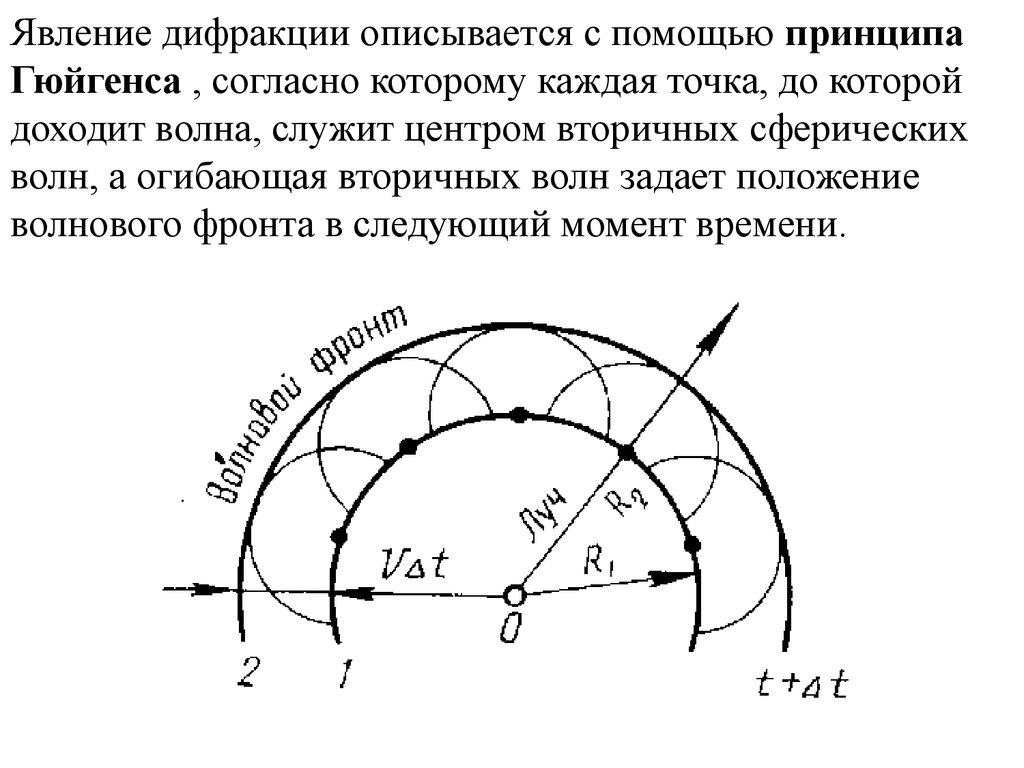
Явление дифракции описывается с помощью принципаГюйгенса , согласно которому каждая точка, до которой
доходит волна, служит центром вторичных сферических
волн, а огибающая вторичных волн задает положение
волнового фронта в следующий момент времени.
12.
Принцип Гюйгенса в его первоначальном видепозволяет находить только положения волнового
фронта в последующие моменты времени, т. е.
определять направление распространения волны.
Принцип Гюйгенса-Френеля
Гипотезу Гюйгенса об огибающей вторичных волн
Френель дополнил физически ясным положением,
согласно которому вторичные волны, приходя в
точку наблюдения, интерферируют друг с
другом. Рисунок иллюстрирует принцип
Гюйгенса–Френеля.
13.
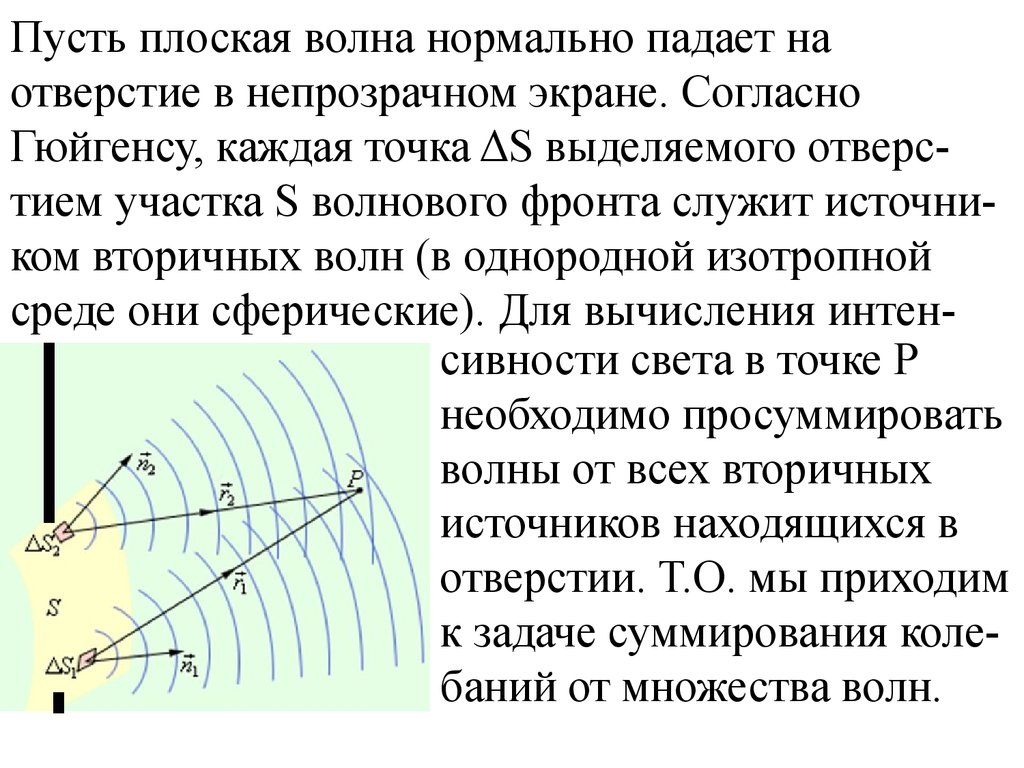
Пусть плоская волна нормально падает наотверстие в непрозрачном экране. Согласно
Гюйгенсу, каждая точка ΔS выделяемого отверстием участка S волнового фронта служит источником вторичных волн (в однородной изотропной
среде они сферические). Для вычисления интенсивности света в точке Р
необходимо просуммировать
волны от всех вторичных
источников находящихся в
отверстии. Т.О. мы приходим
к задаче суммирования колебаний от множества волн.
14.
Мы знаем простой и наглядный метод такогосуммирования, основанный на представлении
колебания в виде вектора. Синусоидальное
колебание величины «а» описывается формулой:
a=Amcos(ωt+φ)
Эту величину можно представить, как проекцию
на горизонтальную ось
вектора с модулем Аm,
который вращается с угловой
скоростью ω. В момент
времени t=0 этот вектор
составлял с горизонтальной
осью угол φ.
15.
Предположим, что имеется второе колебаниеb=Bmcos(ωt+θ)
Мы также изобразим
его на той же плоскости
в виде вращающегося
вектора с длиной Вm
под углом θ к горизонтальной оси.
Пусть величины «а» и «b» складываются образуя
колебание «с»:
с= Amcos(ωt+φ)+ Bmcos(ωt+θ)
Суммарное колебание также буде синусоидальным
и иметь амплитуду Сm и начальную фазу ψ:φ
16.
Для определения этих величин просто сложимВекторы колебаний a и b, определив тем самым
вектор, изображающий суммарное колебание. Благодаря такому приему мы избежали громоздкие
преобразования тригонометрических формул.
Если суммируются несколько колебаний
одинаковой частоты, то для нахождения вектора,
изображающего суммарное колебание,
достаточно просуммировать векторы,
изображающие складываемые колебания. При этом сложение можно выполнять путем подрисовывания к концу
текущего слагаемого начала следующего, как это сделано на рисунке
17.
Воспользуемся данным приемом для нахождения интенсивности света при дифракции на круглом отверстии.возьмем точку наблюдения на перпендикуляре к
центру отверстия. Разобьем мысленно площадь
отверстия на очень узкие кольцевые участки с одинаковой площадью. В пределах каждого из них
расстояние от любой его точки до точки наблюдения одинаково. Каждая точка отверстия представляет собой источник вторичной волны, которая
доставит в точку наблюдения колебание светового
вектора.
18.
При этом колебания, доставленные от точекодного кольцевого участка, будут иметь одинаковую начальную фазу. И при сложении между
собой дадут изображающий вектор под углом к
горизонтальной оси, равным этой фазе.
Колебания, пришедшие от другой зоны будут
иметь другую начальную
фазу и дадут изображающий вектор под другим углом. Просуммировав изображающие векторы колебаний светового вектора
от всех зон, мы получим
вектор суммарного колебания.
19.
Длина этого вектора определит амплитудусветового вектора, а квадрат амплитуды –
интенсивность света в точке наблюдения.
Поскольку условие разбиения на зоны была
одинаковость их площадей, амплитуды колебаний,
доставляемых от них в точку наблюдения, будут
почти одинаковыми. Разности фаз колебаний от соседних зон также получаться
одинаковыми. В результате
картина сложения изображающих векторов будет иметь
вид, показанный на рисунке.
20.
С увеличением номера кольцевого участкаамплитуда колебаний будет немного уменьшаться
вследствие увеличения расстояния от участка до
точки наблюдения. Поэтому картинка сложения
изображающих векторов будет представляю собой
спираль, скручивающуюся в центр окружности
начальных зон. Данная картина называется
спиралью Френеля. Обозначим амплитуду
суммарного изображающего вектора для случая
большого отверстия через Е∞. Если
уменьшать диаметр отверстия, то
внешние зоны, будут закрываться
и престанут давать вклад в суммар-
21.
При этом спираль Френеля будет терять своицентральные витки. Поскольку радиусы
центральных витков малы, длина суммарного
вектора будет изменяться очень мало. Однако при
дальнейшем уменьшении диаметра отверстия
радиусы выбывающих витков спирали Френеля
будут увеличиваться и изменение интенсивности
станут заметными, а затем большими. Внешняя
окружность спирали Френеля представляет
суммирование колебаний от центральной зоны,
крайняя граница которой соответствует
изменению начальной фазы суммируемых
колебаний на π.
22.
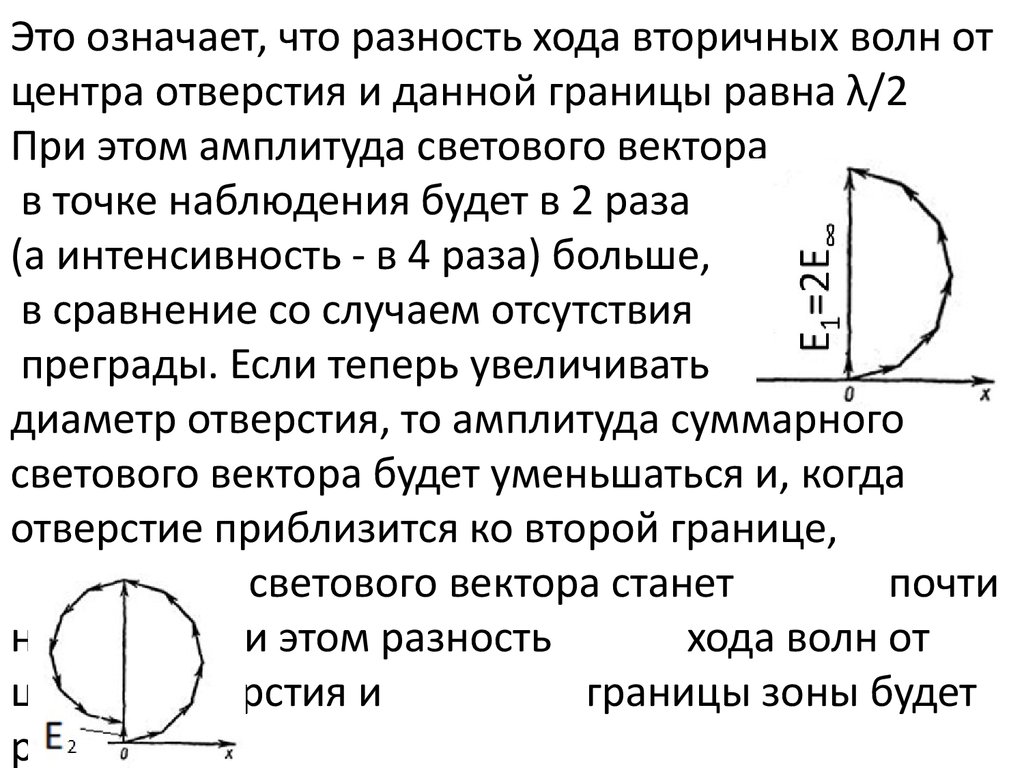
Это означает, что разность хода вторичных волн отцентра отверстия и данной границы равна λ/2
При этом амплитуда светового вектора
в точке наблюдения будет в 2 раза
(а интенсивность - в 4 раза) больше,
в сравнение со случаем отсутствия
преграды. Если теперь увеличивать
диаметр отверстия, то амплитуда суммарного
светового вектора будет уменьшаться и, когда
отверстие приблизится ко второй границе,
амплитуда светового вектора станет
почти
нулевой. При этом разность
хода волн от
центра отверстия и
границы зоны будет
равна λ.
23.
Амплитуда светового вектора в точке наблюденияопределяется разностью хода волн, идущих от
центра и края отверстия в эту точку. Обозначим
эту разность – Δ и выразим ее через радиус
отверстия – r и расстояния от источника до
отверстия – а и от
отверстия до точки
наблюдения – b.
Выразим r Из двух
треугольников:
(35.1)
Первое равенство после раскрытия скобок даст
24.
второе равенство даст уравнениеиз которого выразим х:
. Подставив х в (5.2), получим:
По разности хода центрального и крайних лучей –
Δ, можно определить разность фаз между этими
лучами в точке наблюдения γ=2π Δ /λ. И по разности фаз вычислить модуль суммарного светового
вектора. Из диаграммы векторов, получим: Есум=Е1|sin(γ/2)|
(35.4)
Где Е1 - максимальная амплитуда светового вектора. (Е1=2Е∞)
25.
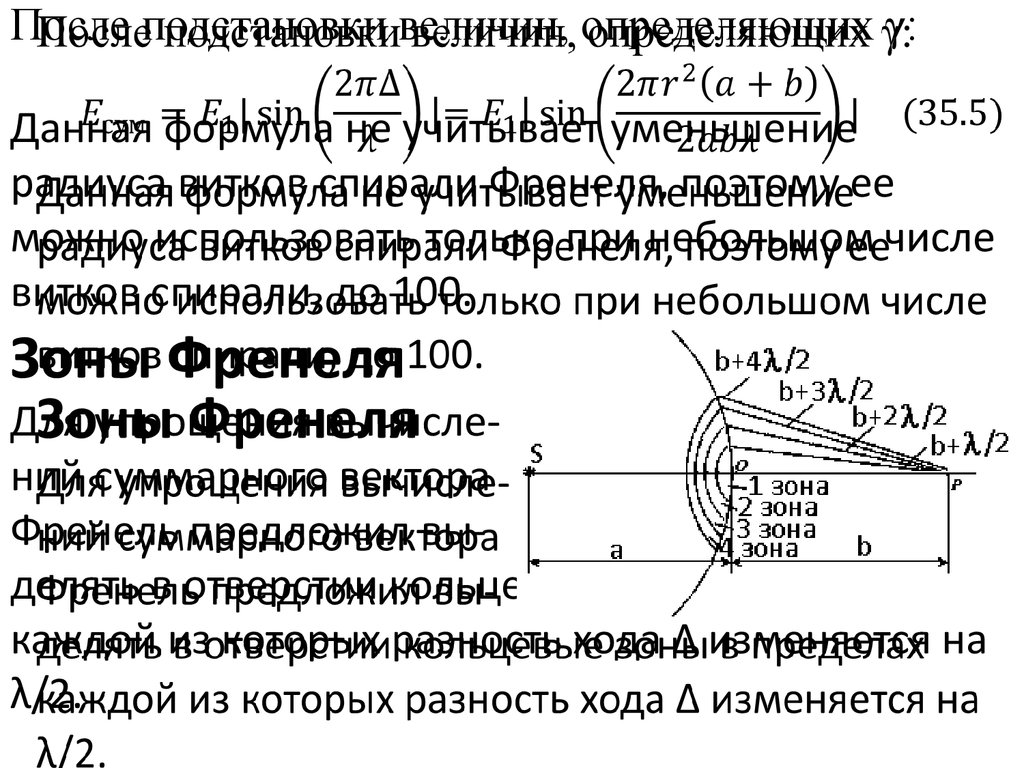
После подстановки величин, определяющих γ:Данная формула не учитывает уменьшение
радиуса витков спирали Френеля, поэтому ее
можно использовать только при небольшом числе
витков спирали, до 100.
Зоны Френеля
Для упрощения вычислений суммарного вектора
Френель предложил выделять в отверстии кольцевые зоны в пределах
каждой из которых разность хода Δ изменяется на
λ/2.
26.
Две соседние зоны Френеля доставляют в точкунаблюдения противофазные колебания почти
равных амплитуд , которые погасят друг друга. В
результате вклад четного числа соседних зон
оказывается нулевым и его можно отбросить при
вычислении суммарного светового вектора. Это
следует из (35.5): аргумент синуса можно
уменьшить на целое число периодов (2π) без
изменения результата.
Радиусы зон Френеля определятся (35.3), если
подставить Δ =mλ/2, где m – номер зоны, тогда:
27.
Пятиминутка. Сколько зон Френеля уместится вотверстии диаметром 0.5 мм, если расстояние от
источника света до отверстия равно 10 см, а от
отверстия до экрана – 10 мм. Длина волны света
равна 550 нм. (Отв. m≈46)
28.
Дифракционная картина от маленького отверстияпредставляет собой чередование светлых и темных
колец. Освещенность центрального пятна определится формулой (35.5). В зависимости от размеров
и длины волны там может быть максимум,
минимум освещенности или промежуточная ее
величина.
Зонные пластинки.
Представим себе прозрачную пластинку на
которую нанесены непрозрачные
кольца, закрывающие четные зоны
Френеля. Вклад этих зон в освещенность центральной точки дифракционной картины будет нуле-
29.
В результате при вычислении освещенностицентральной точки дифракционной картины
вместо спирали Френеля мы получим
картину, показанную на рисунке. Модуль
суммарного светового вектора окажется
значительно больше, чем при отсутствии
преграды. Такая пластинка, которую
называют амплитудной, будет действовать подобно линзе, фокусируя лучи в центральной точке.
Еще более эффективной оказывается фазовая
зонная пластинка, которая не отсекает свет четных
зон Френеля, а увеличивает для них длину
оптического пути на λ/2. Для этого на четных зонах
пластинка чуть более толстая.
30.
В результате мыполучаем плоскую и тонкую
линзу, очень полезную во многих практических случаях.
31.
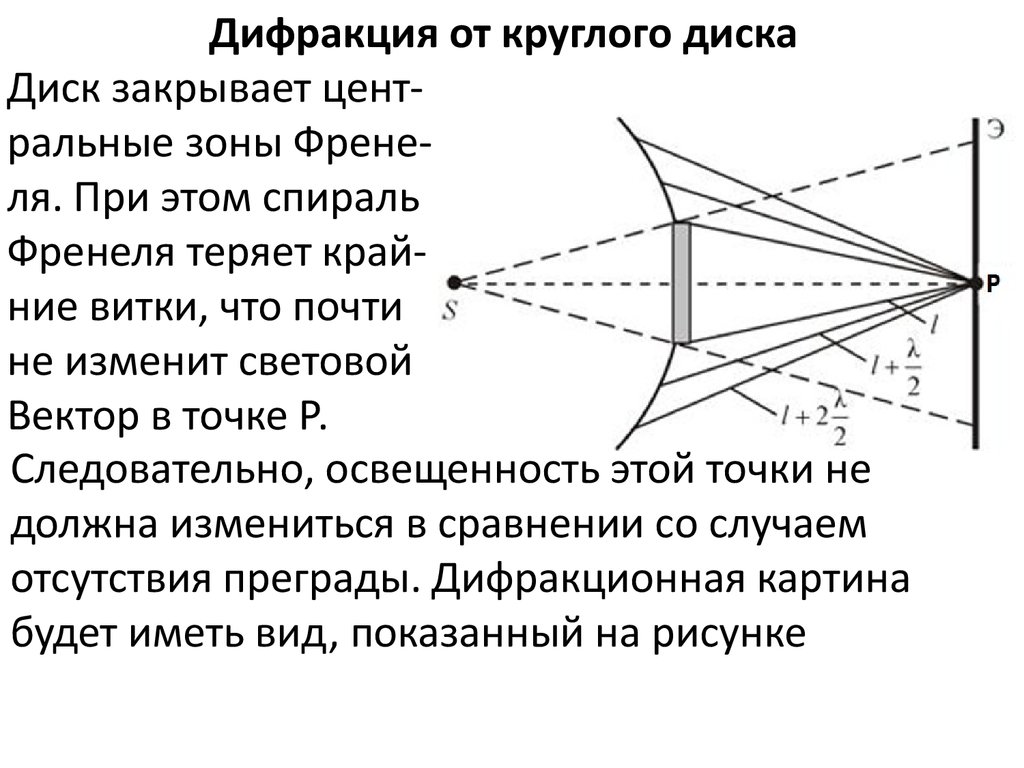
Дифракция от круглого дискаДиск закрывает центральные зоны Френеля. При этом спираль
Френеля теряет крайние витки, что почти
не изменит световой
Вектор в точке Р.
Следовательно, освещенность этой точки не
должна измениться в сравнении со случаем
отсутствия преграды. Дифракционная картина
будет иметь вид, показанный на рисунке
32.
Светлое пятно в центре тени отдиска называется пятном Пуассона.
При опытах вместо диска обычно
используют маленький шарик
Дифракция от прямого края полуплоскости
характеризуется проникновением части световой
энергии в область геометрической тени. В освещенной области (справа от края полуплоскости)
образуется система параллельных краю полос,
период и контрастность которых убывают по мере
удаления от границы
33.
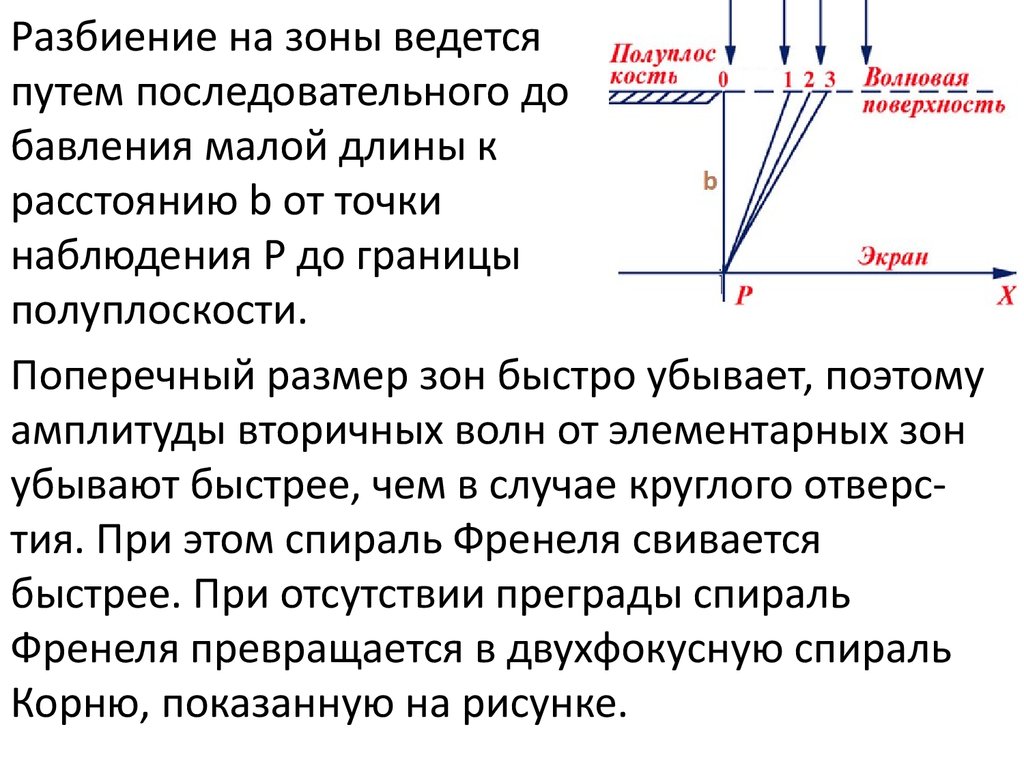
Разбиение на зоны ведетсяпутем последовательного до
бавления малой длины к
расстоянию b от точки
наблюдения P до границы
полуплоскости.
Поперечный размер зон быстро убывает, поэтому
амплитуды вторичных волн от элементарных зон
убывают быстрее, чем в случае круглого отверстия. При этом спираль Френеля свивается
быстрее. При отсутствии преграды спираль
Френеля превращается в двухфокусную спираль
Корню, показанную на рисунке.
34.
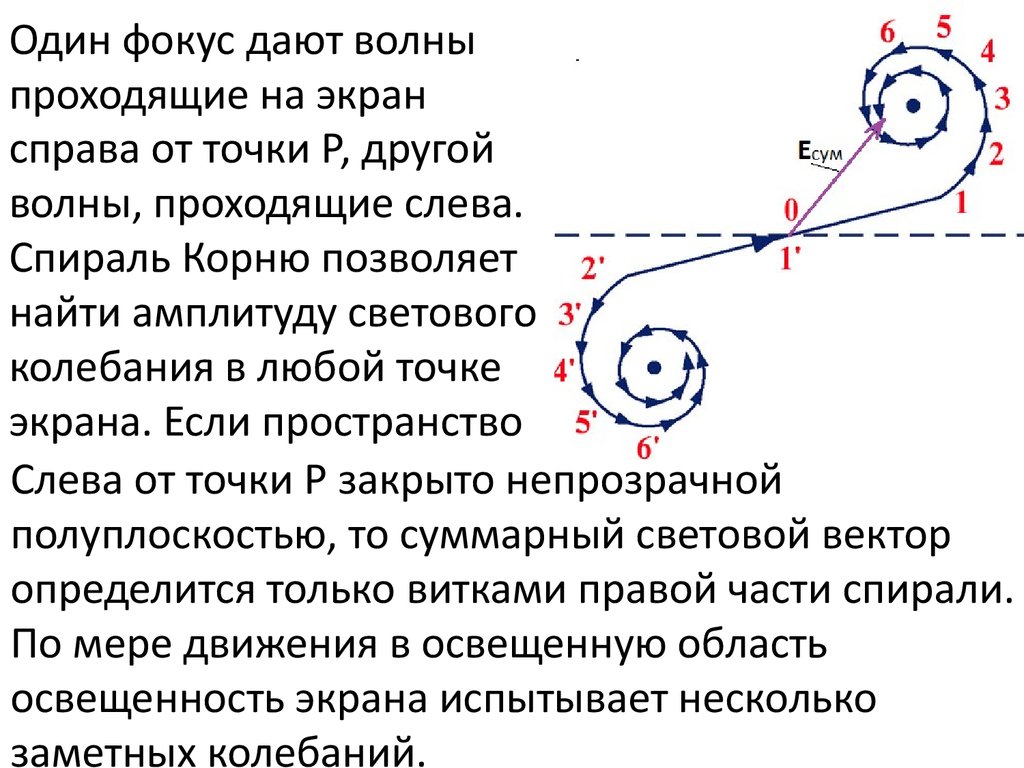
Один фокус дают волныпроходящие на экран
справа от точки Р, другой
волны, проходящие слева.
Спираль Корню позволяет
найти амплитуду светового
колебания в любой точке
экрана. Если пространство
Слева от точки Р закрыто непрозрачной
полуплоскостью, то суммарный световой вектор
определится только витками правой части спирали.
По мере движения в освещенную область
освещенность экрана испытывает несколько
заметных колебаний.
35.
Задача: Фазовая зонная пластинка изготавливаетсяиз стекла с коэффициентом преломления 1.5.
Определить радиусы колец, на которых
необходимо утолщение пластинки и величину
утолщения, если пластинка должна заменить линзу
с оптической силой 15 дптр.

























 physics
physics