Similar presentations:
Раскрытие скобок. 6 класс
1.
2.
Экскурс в историю математических символовНазвание
Знаки,
Черта сверху
выполняющие
произошло
употреблялась
от
роль
введенного
скобок
появились
долго.
Эйлером
в XVв.
Фигурные
скобки
появляются
вочень
сочинениях
Виета
немецкого
В
сочинении
термина
Шюке (1484)
Klammer
выражение,
– «скобки».
которое
(1593)
До
нужно
САпоявления
Взаключить
= С специальных
АВ в скобки,
Декарт,подчеркивается
символов
Ньютон, Лопиталь
перед
выражением,
горизонтальной
которое
чертой.
нужно
А – получили
заключить
M+N
в скобки,
Широкое
применение
скобки
лишь
в
ставилось
Круглые
скобки
слововстречаются
Collect
или благодаря
буквы
у Тартальи
сs отЛейбницу
communis,
(1556), и
первой
половине
XVIII века,
uЗатем
universal
у Жирара
или(1629).
b, означающее
Этописал
почти
binomial,
единственное,
и др.
Бомбелли
(1550)
букву
L перед
еще
больше
Эйлеру.
Lотa+b
что осталосьа в конце
математике
от символов
,
выражением,
выражения
перевернутую
букву.
употребляемых
Жираром.
От
такого обозначения
произошли квадратные скобки.
L
3.
Мы знаем!Распределительный закон умножения.
Раскрытие скобок
a ( b + c ) = ab +ac
4.
Мы знаем!Распределительный закон умножения.
( + ) = ab+ac
ac
Вынесение за скобки
общего множителя
5.
Распределительный закон умножения.Раскрытие скобок
a ( b + c ) = ab +ac
Вынесение за скобки
общего множителя
6.
Применение распределительного закона умножения для быстрого счета.11 73 (10 1) 73 803
19 32 (20 1) 32 608
11 34 374
7.
2+611 26= 286
5+2
11 52= 52
7
8.
Применение распределительного закона умножения для быстрого счета.2
3 5 15 2 17
5
2
2 6 12 4 16
3
9.
Применение распределительного закона умножения для быстрого счета.14 1,5 14 7 21
25 1,5 25 12,5
37,5
10.
++(+)
+
–(–)
–
–(+)
11.
+(–3x+2b–m)=+(–3x+2b–m)
Если перед скобками стоит знак «+»,
то при раскрытии скобок знаки
слагаемых в скобках сохраняются.
12.
+(x–2n–k)=+(x–2n–k )
Если перед скобками стоит знак «+»,
то при раскрытии скобок знаки
слагаемых в скобках сохраняются.
13.
–(–2x+4+b–k) =– (+
– 2x+4
– +
– b+
– k)
Если перед скобками стоит знак «–»,
то при раскрытии скобок знаки
слагаемых в скобках заменяются
на противоположные.
14.
–(+2x+3f–m–h) =–+
–(2x+
– 3f +
– m+
–h)
Если перед скобками стоит знак «–»,
то при раскрытии скобок знаки
слагаемых в скобках заменяются
на противоположные.
15.
–( 4 + x –6) +x=–4–x+6+x
=2
16.
–(–2x+4)+(b–2x) =– (+
– 2x+4
– ) +(b –2x)
=b–4
17.
–(a+b)=–a
+a
–b
+b
–(a–b)=
–a
+b
+a
–b
+у
–у
–х
+х
d
+t
–(–х+у)=
d–(–k+t)=
–m+(a – c)=
–c
+c
–t
–k
+k
–m
–a
+a
+s
–r +n –n
p –(–n+ r –s)=
p +r –s
–(k+t)+(–a–s)=
–k +k +t –t
–(d–x)–(y–z)=
+d –d –x +x +y –y +z –z
–a +a –s +s
Раскрой скобки. Щелкни мышкой по выражениям, которые считаешь
правильными. Не ошибайся, твои ошибки все увидят!
18.
Для раскрытия скобок используемраспределительный закон умножения.
-3(4x –5)= -12x+15
19.
-2(-4x–3) = 8x +620.
–2( 3x –1) = –6x+221.
-3(4x –5) –2( 3x –1)= -12x+15 –6x+2
= -18x+17






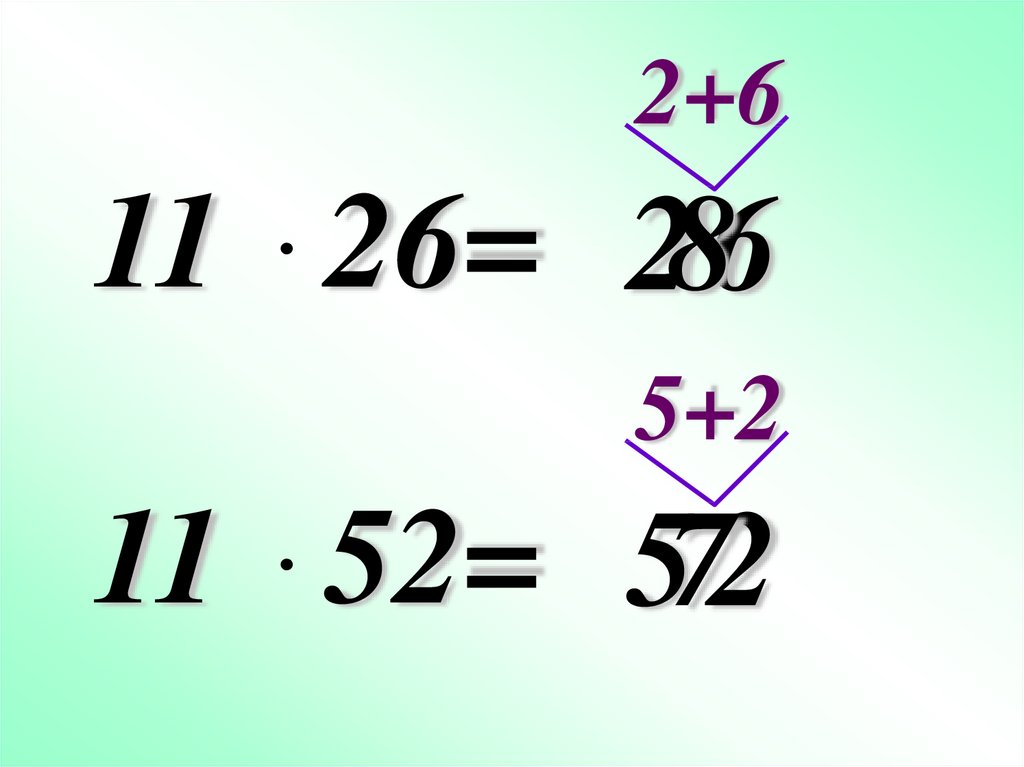







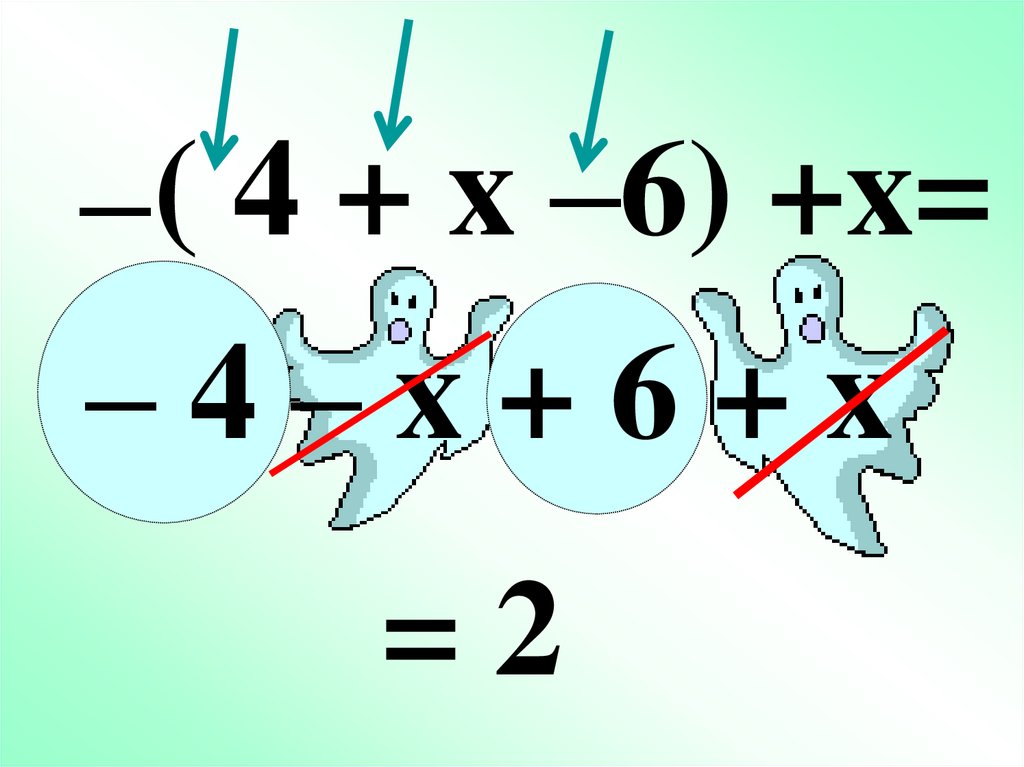






 mathematics
mathematics








