Similar presentations:
Комбинаторные задачи на перестановки, размещения
1. ДОБРОЕ УТРО!
На предыдущих уроках мы с вамирешали комбинаторные задачи на
перестановки, размещения.
2.
Мы говорили о том, чторазличают 3 вида соединений:
размещения, перестановки и
сочетания.
Это зависит от того, входят ли в
соединения все элементы
данного множества или только
часть их, играет ли роль
порядок элементов или не
играет.
06.04.2020
2
3.
• Вспомним различие задач наперестановки и размещения. На
следующем слайде будут представлены
основные различия этих задач.
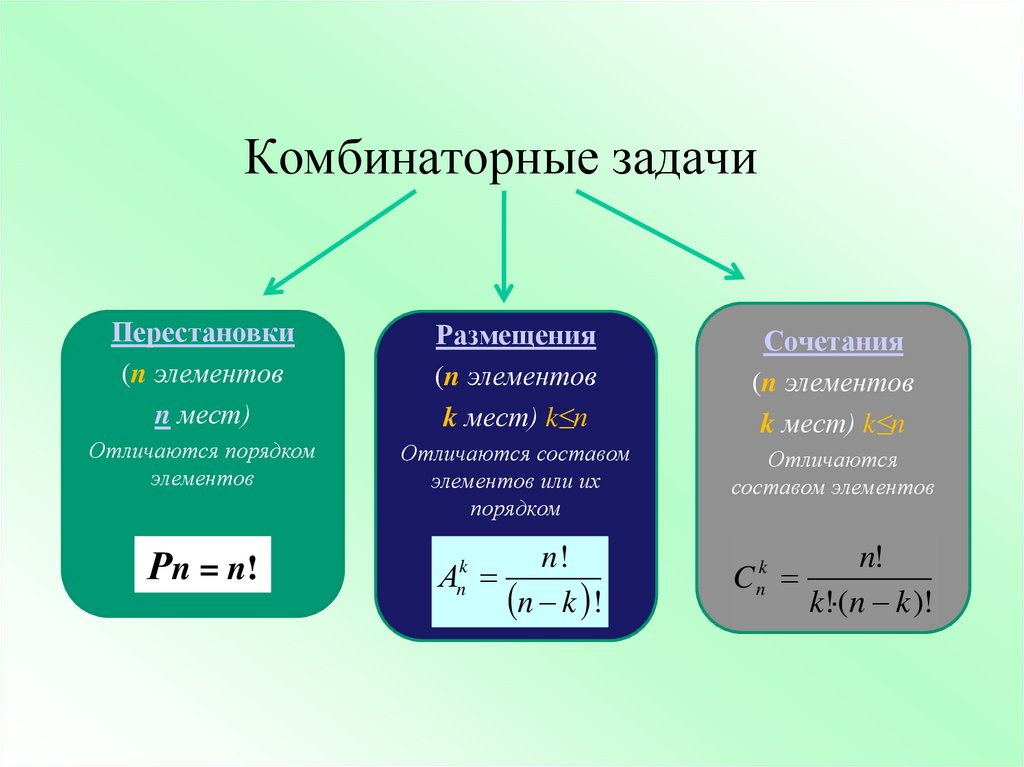
4. Комбинаторные задачи
Факториал n! =1·2·3·…·(n – 1)·nКомбинаторные задачи
Перестановки
(n элементов
n мест)
Размещения
(n элементов
k мест) k≤п
Отличаются порядком
элементов
Отличаются составом
элементов или их
порядком
Рn = n!
n!
А
n k !
k
n
Сочетания
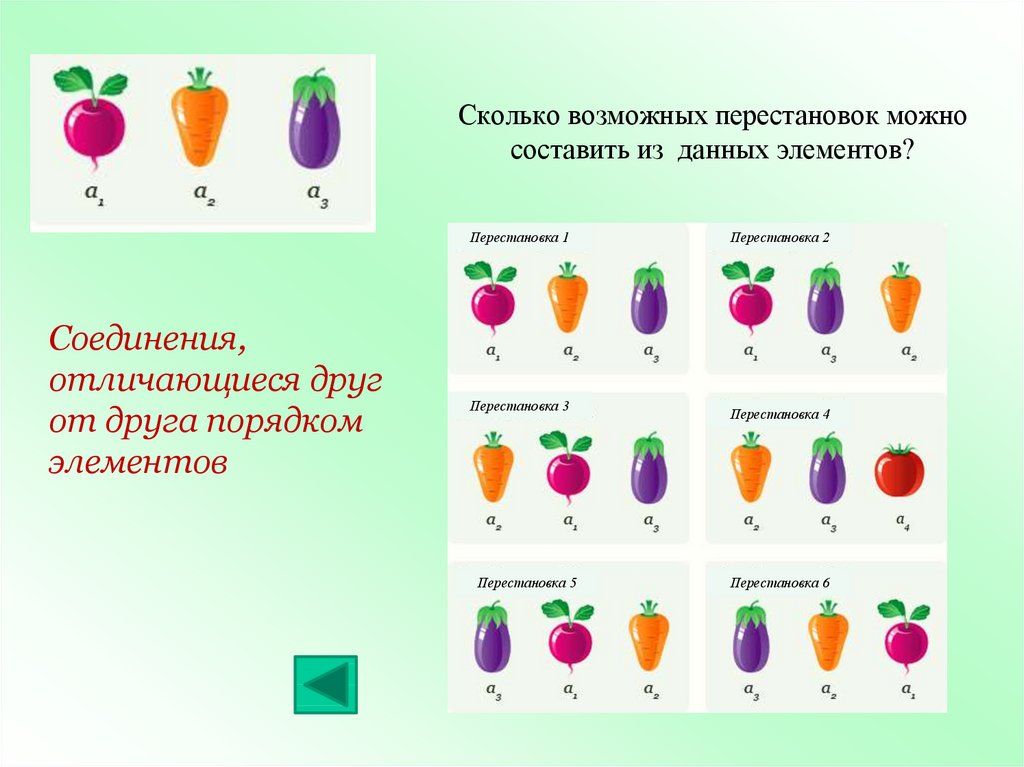
5. Сколько возможных перестановок можно составить из данных элементов?
Перестановка 1Соединения,
отличающиеся друг
от друга порядком
элементов
Перестановка 3
Перестановка 5
Перестановка 2
Перестановка 4
Перестановка 6
6. Сколько возможных размещений по 2 можно составить из данных элементов?
Соединения,отличающиеся друг
от друга составом
элементов или их
порядком
7. Определите тип задачи и реши её
• В турнире участвуют пять команд. Сколько вариантовраспределения мест между ними возможно?
• Учащиеся 2 класса изучают 9 предметов. Сколькими
способами можно составить расписание на один день,
чтобы в нем было 4 различных предмета?
• Сколькими способами можно смешать по три краски из
имеющихся пяти?
8.
• ВНИМАНИЕ!• Задача № 3 отличается от задачи на
перестановки и размещения.
• Такие задачи сегодня будем учиться
решать!
9. Сочетания
Тема урока:06.04.2020
Сочетания
9 класс
9
10. Решение
ba
c
d
e
Выпишем возможные варианты смешивания красок,
учитывая, что от порядка расположения красок результат
не зависит:
abc, abd, abe, acd, ace, ade,
bcd, bce, bde
Cde
Указаны различные способы смешивания красок, в которых
по-разному сочетаются три краски из данных пяти.
Говорят, что составлены все возможные
сочетания из 5 элементов по 3.
11. Сочетания
• Число всех выборов k элементов из n данных без учётапорядка называют числом сочетаний из n элементов по k.
Обозначается С n
k
n!
C
k!(n k )!
k
n
12. Комбинаторные задачи
Перестановки(n элементов
n мест)
Размещения
(n элементов
k мест) k≤п
Отличаются порядком
элементов
Сочетания
(n элементов
k мест) k≤п
Отличаются составом
элементов или их
порядком
Отличаются
составом элементов
Рn = n!
n!
А
n k !
n!
C
k! (n k )!
k
n
k
n
13. Сколько возможных сочетаний по 2 можно составить из данных элементов?
Соединения,отличающиеся друг
от друга составом
элементов
14. Посчитайте, сколько возможных сочетаний по 3 можно составить из данных предметов
СамостоятельноПосчитайте, сколько возможных сочетаний по 3
можно составить из данных предметов
Л
Р
Л
К
Т
15.
Простейшие комбинацииПерестановки
Размещения
Сочетания
Из n элементов
по n элементов
Из n элементов
по k элементов
Из n элементов
по k элементов
Порядок имеет
значение
Порядок имеет
значение
Порядок не имеет
значения
Рn n!
06.04.2020
Аn
k
n!
n k !
Сn
k
n!
n k ! k!
15
16.
Решите задачи:№ 768, 769, 774.
Проверка
06.04.2020
16
17.
№ 768.В классе 7 человек успешно занимаются математикой.
Сколькими способами можно выбрать из них двоих
для участия в математической олимпиаде?
Решение:
7!
7!
5! 6 7 6 7
2
C7
21
2
2!(7 2)! 2! 5! 1 2 5!
06.04.2020
17
18.
№ 769.В магазине «Филателия» продается 8
различных наборов марок, посвященных
спортивной тематике. Сколькими
способами можно выбрать из них 3
набора?
Решение:
8! 8 7 6
Ñ
56(ñï .)
5! 3! 1 2 3
3
8
06.04.2020
18
19.
№ 774.Бригада, занимающаяся ремонтом школы, состоит из
12 маляров и 5 плотников. Из них для ремонта
физкультурного зала надо выделить 4 маляров и 2
плотников. Сколькими способами можно это
сделать?
Решение:
12! 5! 9 10 11 12 4 5
4
2
С12 C5
4! 8! 2! 3!
2 3 4
2
3 5 11 3 2 5 4950(сп.)
06.04.2020
19
20. Задача
У одного ученика есть 11 книг поматематике, а у другого – 15.
Сколькими способами они могут
выбрать по 3 книги каждый для
обмена?
11! 15!
k C C
2
(3!) 8! 12!
3
11
3
15
06.04.2020
20
21. Задача
У 6 взрослых и 11 детей обнаруженыпризнаки инфекционного заболевания.
Чтобы проверить диагноз выбирают 2-х
взрослых и 3-х детей для сдачи анализов.
Сколькими способами можно это сделать?
6! 11!
k C C
2! 4! 3! 8!
2
6
3
11
06.04.2020
21
22. Задача
В шахматном кружке занимаются 2девочки и 7 мальчиков. Для участия в
соревнованиях необходимо составить
команду из 4 человек, в которую должна
входить хотя бы одна девочка. Сколькими
способами можно это сделать?
k C C C
2
7
1
2
3
7
06.04.2020
22
23. Задача
Сколькими способами можноразбить 10 человек на две
баскетбольные команды по
5 человек в каждой?
5
10
C
k
2
06.04.2020
23





















 mathematics
mathematics








