Элементы теории бинарных отношений. Формы представления отношений. Операции над отношениями

1.

Лекция
Элементы теории бинарных отношений
1. Формы представления отношений
2. Операции над отношениями
Говорить об отношениях можно тогда, когда имеется множество А элементов, на которых эти отношения
определены. Само множество А называют множеством-носителем отношений.
Отношение R – подмножество конечного множества декартовой степени Аk = Аn1×А n2×А n3× …×Аnk заданного
множества А = { а1, а2,…,аn }
Подмножество R А
называется k-арным отношением в множестве А или над множеством А. Число k
называется рангом или местностью отношения R. Подмножество R Аk называется также k-местным или k-арным
предикатом на множестве А.
Множество U = Аk и пустое множество в Аk называются соответственно
универсальным отношением и нуль
отношением ранга k в множестве А.
Диагональ множества, т.е. множество Е = {(а1,а2,…,аn )| аi Аik , i = 1(1)n}, называется отношением равенства в
множестве А. Множество всех n-арных отношений в множестве А относительно операций ∪,∩ является булевой
алгеброй. Бинарное отношение – подмножество множества А×А=A2 упорядоченных пар {(аi , аj)} элементов
заданного множества А = {(а1,а2,…, аi ,…, аj ,…,а|A| )|аi Аi, i = 1(1)|A|}.
k
О п р е д е л е н и е . Каждый (любой) элемент булеана называется бинарным отношением.
Наряду с теоретико-множественными операциями объединения, пересечения , разности (\), симметрической
разности (∆), дополнения (R’) для бинарных отношений рассматривают также специальные операции: обращения
отношений , умножение отношений и др.
Отношением называется пара , R , где – множество-носитель, a R –
подмножество декартова произведения , т.е. R . Содержательный
смысл такого определения состоит в том, что задание подмножества R в
множестве определяет, какие пары находятся в отношении R. Пусть
x , y , тогда если пара (х, у) входит в R, т.е. x , y R , то будем записывать xRy,
что читается «пара (х, у) находится в отношении R».

2.

1. Формы представления отношений
1. Представление перечислением элементов отношения. Для того чтобы задать
отношение , R на множестве , необходимо перечислить все пары
x , y , которые содержатся в R.
2. Матричное представление. Пусть множество x 1 , x 2 , ..., x n , где n , R –
отношение на . Построим квадратную матрицу A n n . Ее i-я строка
соответствует i-му элементу x i множества , а j-й столбец – элементу x j . На
пересечении i-й строки и j-го столбца ставится единица, если выполнено
x i , x j R ,
и нуль – в противном случае. Обозначим элемент, стоящий на пересечении i-й
строки и j-го столбца, через a ij .
Общее правило задания матрицы отношения A n n a ij nn формулируется так
1, если пара xi , x j R
aij
i , j 1 1 n.
0
,
если
пара
x
,
x
R
i
j
Пример 2.2. Представления отношения А в матричной форме будет выглядеть следующим образом:
A[4×4] =
С[4×4] =
x1
x2
x3
x4
x1
0
1
1
0
x2
0
0
1
1
x3
0
1
0
1
x4
0
x1
1
5
9
13
0
x2
2
6
10
14
0
x3
3
7
11
15
0
x4
4
8
12
16
x1
x2
x3
x4
.

3.

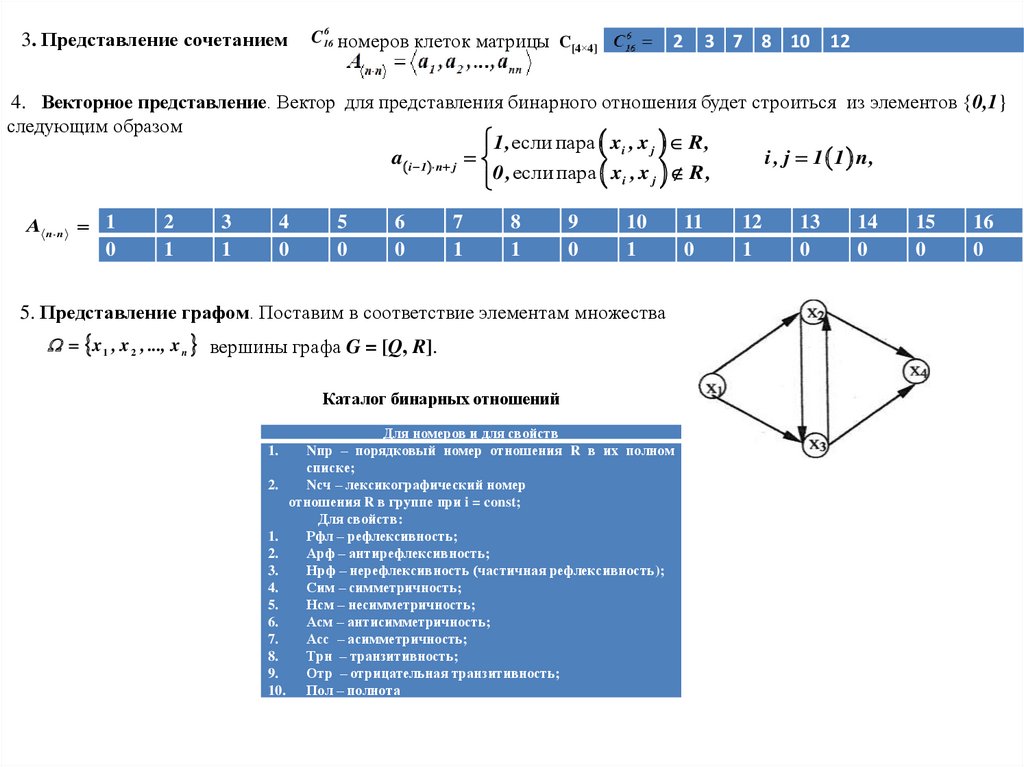
3. Представление сочетанием
6
C 16
номеров клеток матрицы С[4×4]
2
3 7 8 10 12
4. Векторное представление. Вектор для представления бинарного отношения будет строиться из элементов {0,1}
следующим образом
1, если пара xi , x j R,
a i 1 n j
i , j 1 1 n,
0
,
если
пара
x
,
x
R,
i
j
A n n 1
0
2
1
3
1
4
0
5
0
6
0
7
1
8
1
9
0
10
1
5. Представление графом. Поставим в соответствие элементам множества
x 1 , x 2 , ..., x n вершины графа G = [Q, R].
Каталог бинарных отношений
Для номеров и для свойств
Nпр – порядковый номер отношения R в их полном
списке;
2.
Nсч – лексикографический номер
отношения R в группе при i = const;
Для свойств:
1.
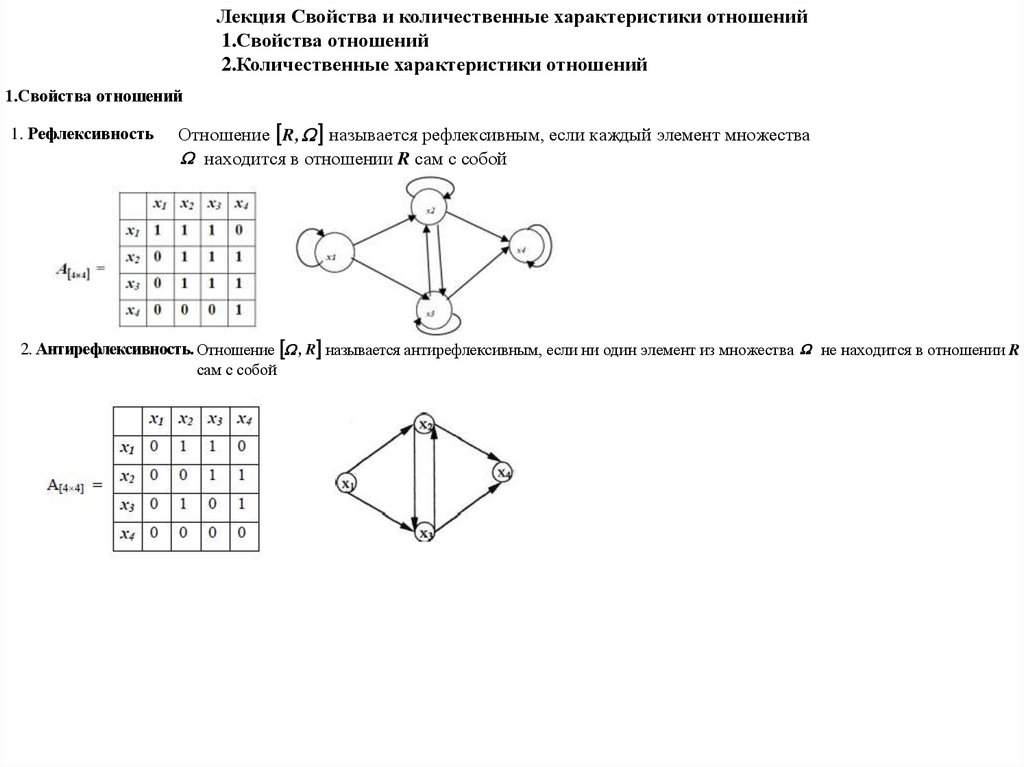
Рфл – рефлексивность;
2.
Арф – антирефлексивность;
3.
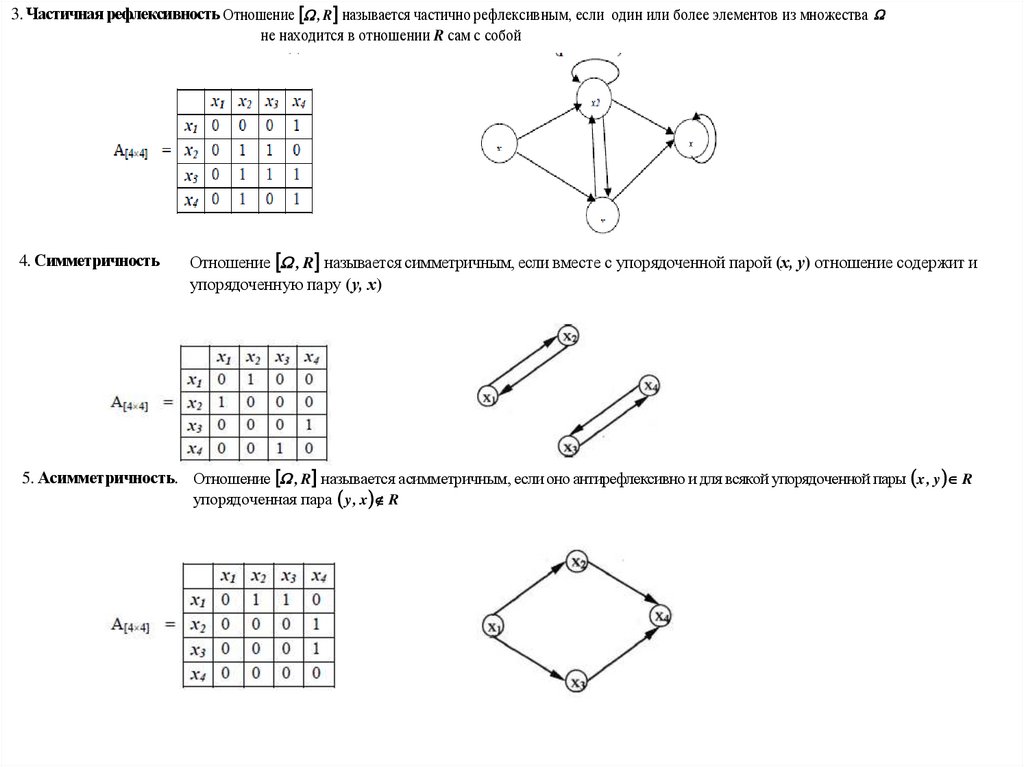
Нрф – нерефлексивность (частичная рефлексивность);
4.
Сим – симметричность;
5.
Нсм – несимметричность;
6.
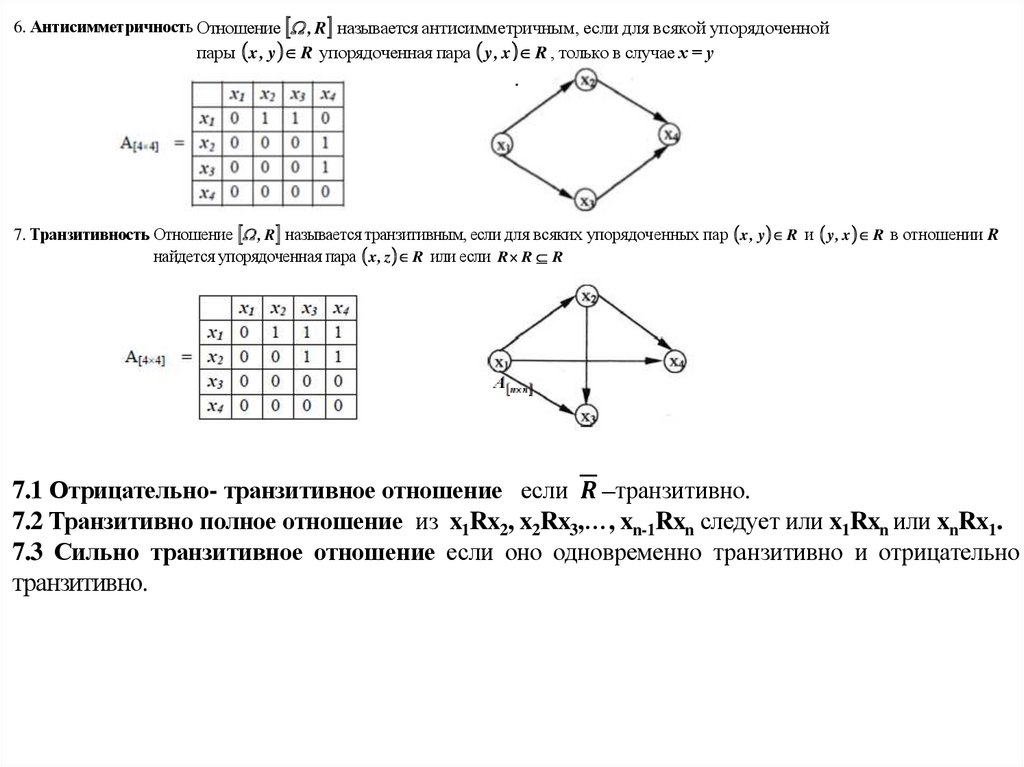
Асм – антисимметричность;
7.
Асс – асимметричность;
8.
Трн – транзитивность;
9.
Отр – отрицательная транзитивность;
10. Пол – полнота
1.
11
0
12
1
13
0
14
0
15
0
16
0

4.

2. Операции над отношениями
P=
1
1
1
1
1
1
1
1
1
1
1
,Q=
1
1
1
1
Бинарные операции
1. Пересечение (P Q) – отношение, образованное всеми теми парами, которые входят в оба отношения,
т.е. общие для P и Q
P Q = {< ai aj > | (< ai aj > P)&(< ai aj > Q)}
1
P Q =
1
1
2. Объединение (P Q) - отношение, определяемое объединением соответствующих подмножеств из А А
Отношение, образованное всеми парами, составляющими или отношение P или отношение Q, т.е. парами,
принадлежащими хотя бы одному из отношений.
P Q = {< ai aj > | (< ai aj > P) ( < ai aj > Q)}.
P Q =
1
1
1
1
1
1
1
1
1
1
1
1

5.

3. Композиция или произведение (P∙Q) - отношение, образованное всеми парами, для которых выполняется:
P∙Q = {< ai aj > | (< ai ak > P) & (< ak aj > Q)}.
Композиция (Р Q) на множестве М – отношение R, заданное на том же множестве М, которое содержит пару (x, y), когда
существует Z M такое, что (x, z) P и (z, y) Q.
1 0 0 0
1 1 0 0
1 1 1 0
1 0 0 1
P=
x1
0
0
1
1
x2
0
1
0
1
x1 x2
0
1
1
1
1
0
0
0
Q=
x1
0
0
1
1
x2
0
1
0
1
1
1
1
1
0
1
1
0
0
1
0
0
P° Q =
1
1
1
1
1
1
1
1
0
1
1
0
0
1
1
0
x1&x2
0
0
0
1
4. Разность (P\Q)- отношение, образованное теми парами из Р, которые не входят в отношение Q
P\Q = {< ai aj > | (< ai aj > P)&( < ai aj > Q)}.
1
1
1 1
P\Q =
Q\P =
1
1
1
1
1
5. Симметрическая разность (P Q)- отношение, образованное теми парами, которые входят в объединение P Q,
но не входят в пересечение P Q.
Другая форма определения объясняет название операции: P Q образовано теми упорядоченными парами, которые являются
объединением разностей P\Q и Q\P. Таким образом, выражение для симметрической разности записывается двумя разными
способами:
1
P Q =
1
1
1
1
1
1
1
1
P Q = (P Q)\(P Q) = (P\Q) (Q\P).

6.

Унарные операции над отношениями
6. Дополнение
P
Отношение R является дополнением отношения R,
если оно выполняется для тех и только для тех пар,
для которых не выполняется отношение R.
Дополнение к отношениям – такое отношение,
которое образовано парами, не входящими в
соответствующие отношения.
ഥ
Р
P { i , j | ( i , j A A ) & ( i , j P )}
P A A\ P
P
7. Обращение отношений. Обратным к отношению R называется отношение R
определяемое условием
1
,