Логические задачи. Логические операции

1. Логические задачи

2. Логические операции

• Логическая операция - способ
построения сложного высказывания из
данных высказываний, при котором
значение истинности сложного
высказывания полностью определяется
значениями исходных высказываний.

3.

Логическое отрицание
(инверсия)
Логическое отрицание (инверсия)
образуется из высказывания с
помощью добавления частицы «не» к
сказуемому или использования
оборота речи «неверно, что…».
Обозначение инверсии: НЕ А;

4.

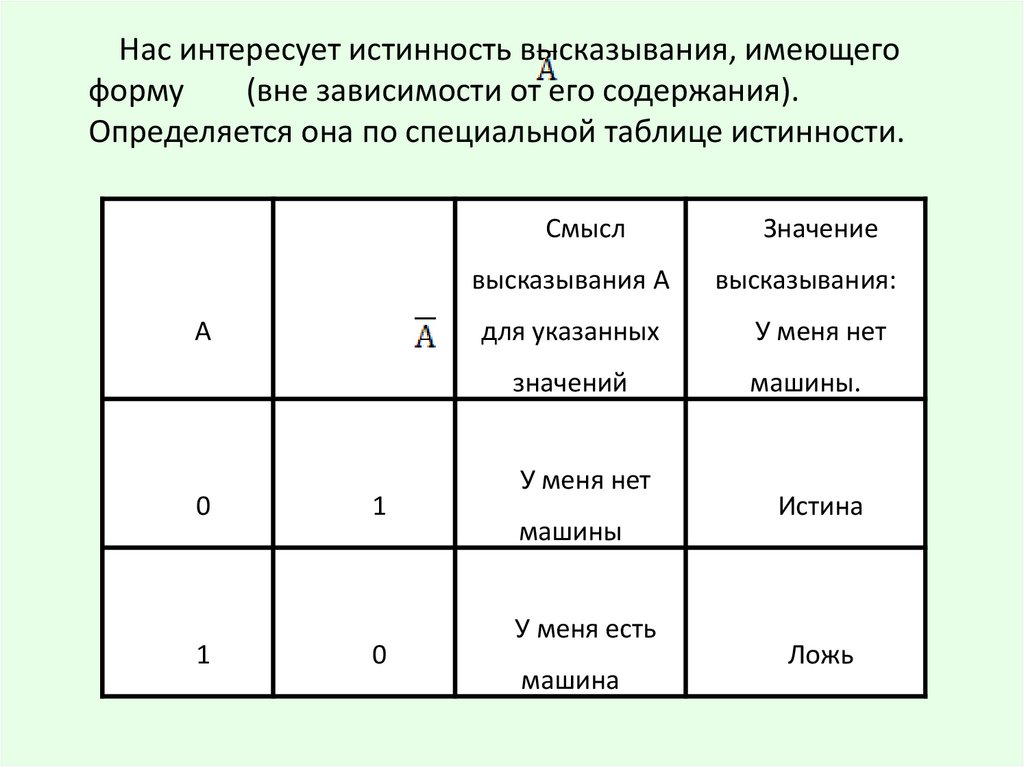
Нас интересует истинность высказывания, имеющего
форму
(вне зависимости от его содержания).
Определяется она по специальной таблице истинности.
Смысл
высказывания А
А
для указанных
значений
0
1
1
0
У меня нет
машины
У меня есть
машина
Значение
высказывания:
У меня нет
машины.
Истина
Ложь

5.

Логическое
умножение(конъюнкция)
Логическое умножение
(конъюнкция) образуется
соединением двух высказываний в
одно с помощью союза «и».
Обозначение конъюнкции:
А И В; А ∧ В; А & В;

6.

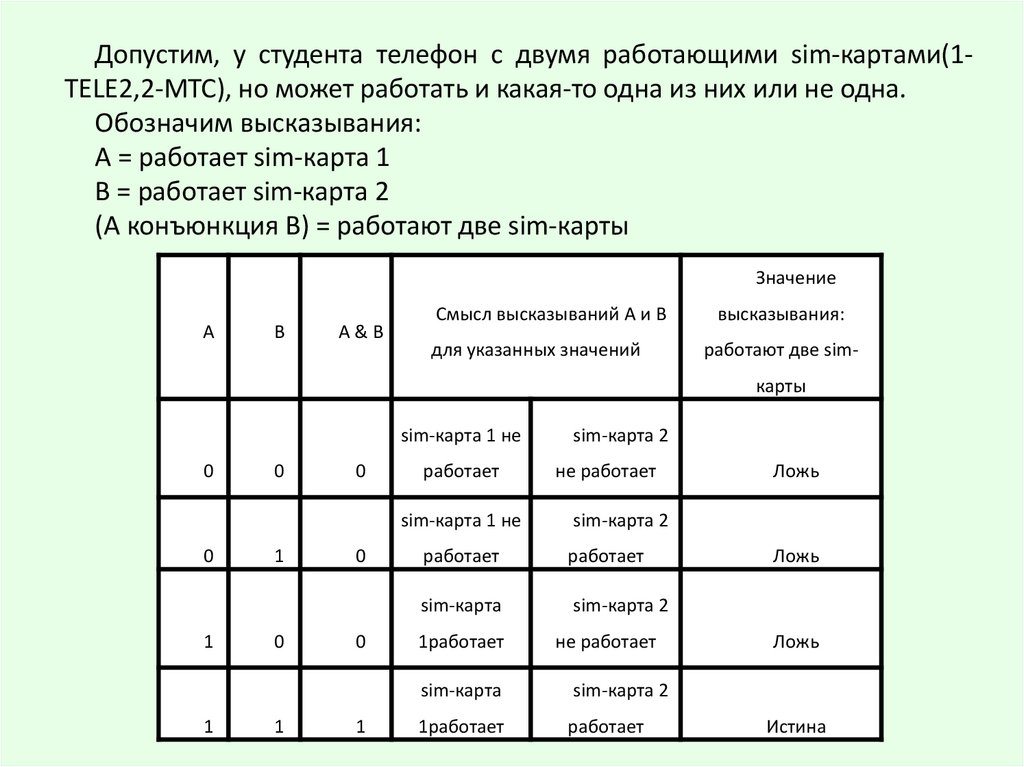
Допустим, у студента телефон с двумя работающими sim-картами(1TELE2,2-МТС), но может работать и какая-то одна из них или не одна.
Обозначим высказывания:
А = работает sim-карта 1
В = работает sim-карта 2
(А конъюнкция В) = работают две sim-карты
Значение
А
В
А&В
Смысл высказываний А и В
для указанных значений
высказывания:
работают две simкарты
sim-карта 1 не
0
0
0
работает
sim-карта 1 не
0
1
1
1
0
1
0
0
1
sim-карта 2
не работает
sim-карта 2
работает
работает
sim-карта
sim-карта 2
1работает
Ложь
не работает
sim-карта
sim-карта 2
1работает
работает
Ложь
Ложь
Истина

7.

Логическое сложение
(дизъюнкция).
Логическое сложение
(дизъюнкция) образуется
соединением двух высказываний в
одно с помощью союза «или».
Обозначение нестрогой дизъюнкции:
А ИЛИ В; А ∨ В; А + В.

8.

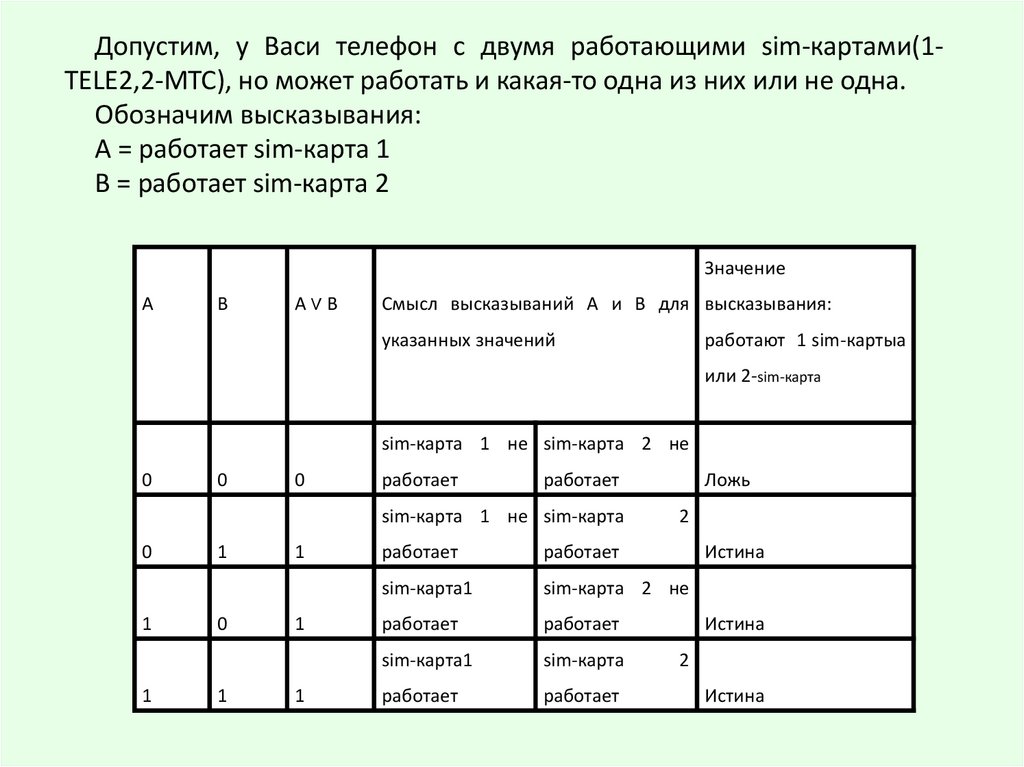
Допустим, у Васи телефон с двумя работающими sim-картами(1TELE2,2-МТС), но может работать и какая-то одна из них или не одна.
Обозначим высказывания:
А = работает sim-карта 1
В = работает sim-карта 2
Значение
А
В
А∨В
Смысл высказываний А и В для высказывания:
указанных значений
работают 1 sim-картыа
или 2-sim-карта
sim-карта 1 не sim-карта 2 не
0
0
0
работает
работает
sim-карта 1 не sim-карта
0
1
1
1
0
1
1
1
1
Ложь
2
работает
работает
Истина
sim-карта1
sim-карта 2 не
работает
работает
sim-карта1
sim-карта
работает
работает
Истина
2
Истина

9.

Логическое следование
(импликация).
Логическое следование (импликация)
образуется соединением двух
высказываний в одно с помощью оборота
речи «если . . ., то . . .».
Обозначение импликации:
А→В; А
В.

10.

Пусть даны высказывания:
А = Кондиционер включен.
В = В комнате свежо.
(А импликация В) = Если кондиционер включен, то в комнате
свежо.
Значение
А
В
А → В
Смысл высказываний А и В
для указанных значений
высказывания:
Если кондиционер
включен, то в комнате
свежо..
0
0
1
1
0
1
0
1
1
1
0
1
Кондиционе
В комнате
р выключен
душно
Кондиционе
В комнате
р выключен
свежо
Кондиционе
В комнате
р включен
душно
Кондиционе
В комнате
р включен
свежо
Истина
Истина
Ложь
Истина

11.

Логическое равенство
(эквивалентность).
Логическое равенство
(эквивалентность) образуется
соединением двух высказываний в
одно при помощи оборота речи « . . .
тогда и только тогда, когда . . .».
Обозначение эквивалентности: А
В.

12.

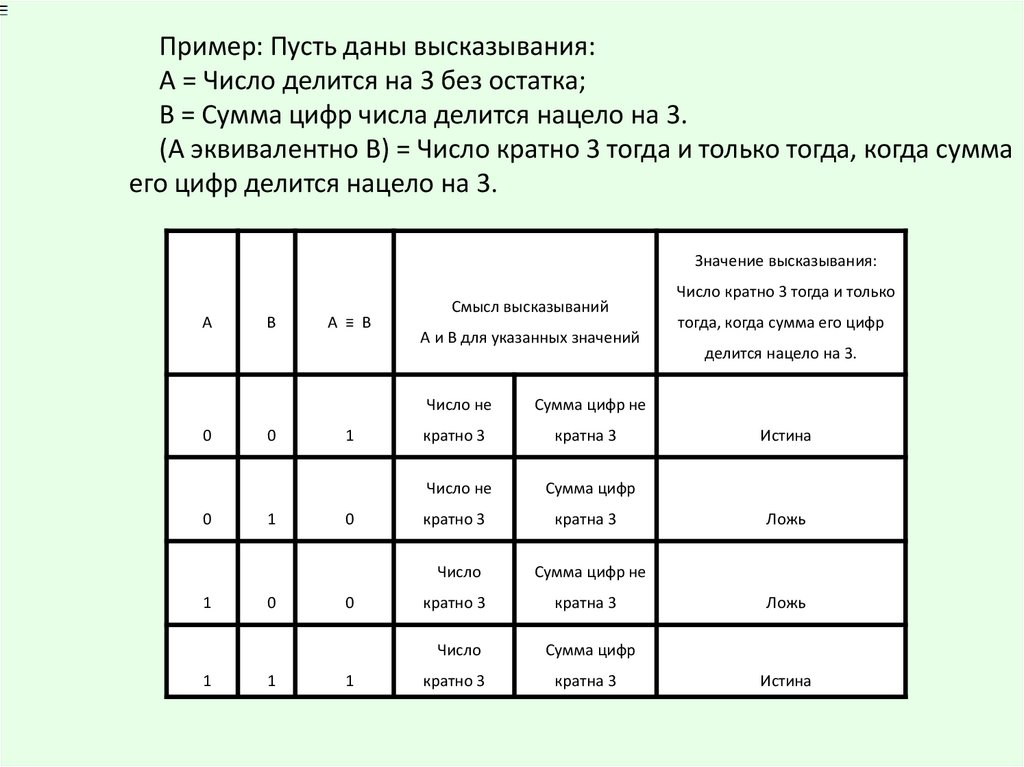
Пример: Пусть даны высказывания:
А = Число делится на 3 без остатка;
В = Сумма цифр числа делится нацело на 3.
(А эквивалентно В) = Число кратно 3 тогда и только тогда, когда сумма
его цифр делится нацело на 3.
Значение высказывания:
А
0
0
1
1
В
0
1
0
1
А ≡ В
1
0
0
1
Смысл высказываний
А и В для указанных значений
Число не
Сумма цифр не
кратно 3
кратна 3
Число не
Сумма цифр
кратно 3
кратна 3
Число
Сумма цифр не
кратно 3
кратна 3
Число
Сумма цифр
кратно 3
кратна 3
Число кратно 3 тогда и только
тогда, когда сумма его цифр
делится нацело на 3.
Истина
Ложь
Ложь
Истина

13.

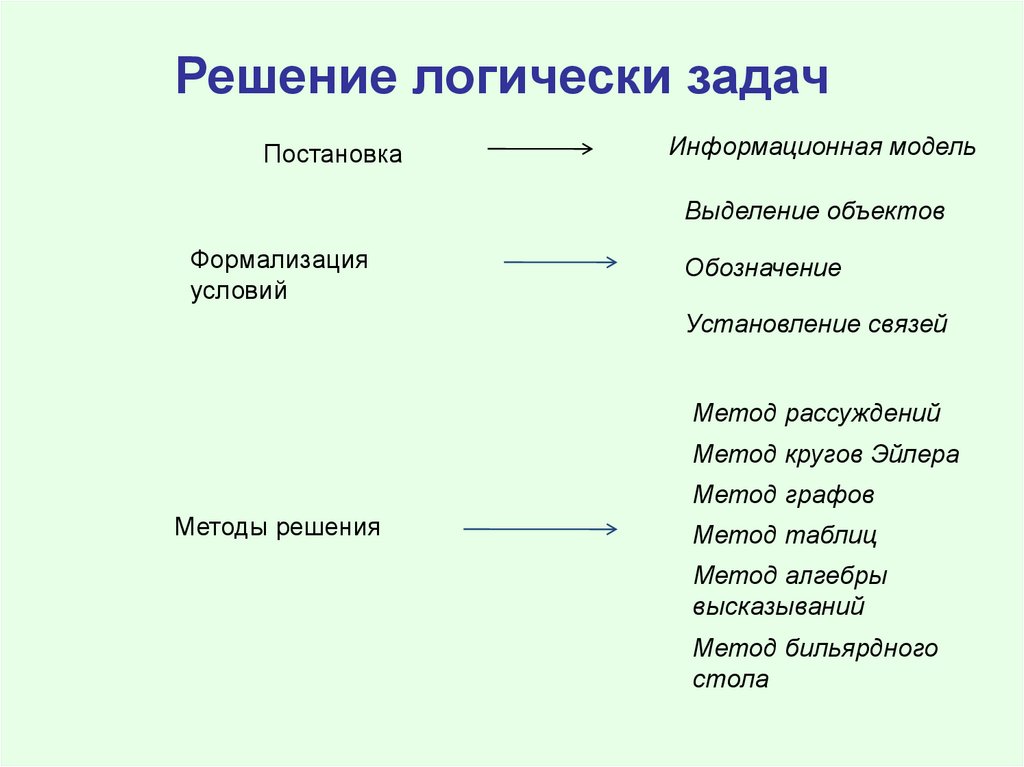
Решение логически задач
Постановка
Информационная модель
Выделение объектов
Формализация
условий
Обозначение
Установление связей
Метод рассуждений
Метод кругов Эйлера
Метод графов
Методы решения
Метод таблиц
Метод алгебры
высказываний
Метод бильярдного
стола

14.

Решение задач с помощью
алгебры логики
При составление расписания на
понедельник преподаватели просили,
чтобы занятия проходили в следующем
порядке:
1. Астрономия (1 или 4 пара)
2. История математики (2 или 3 пара)
3. Физика (3 пара)
4. Химия (1 или 5 пара)

15.

Элементарные высказывания:

16.

17.

18.

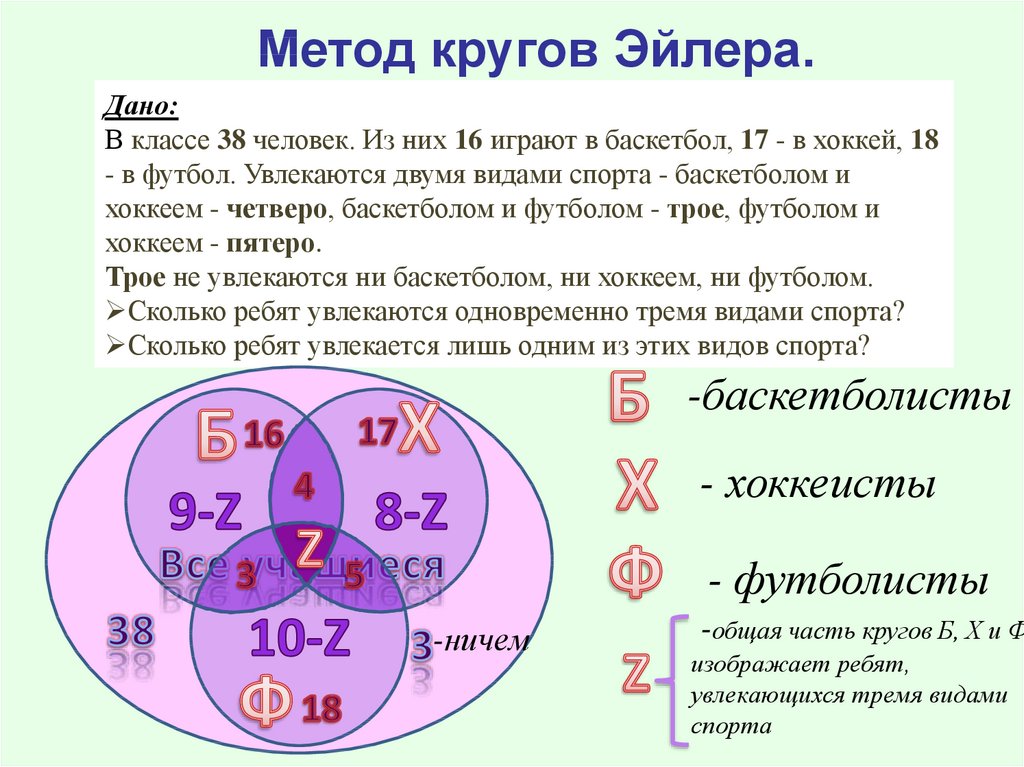
Метод кругов Эйлера.
Дано:
В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18
- в футбол. Увлекаются двумя видами спорта - баскетболом и
хоккеем - четверо, баскетболом и футболом - трое, футболом и
хоккеем - пятеро.
Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.
Сколько ребят увлекаются одновременно тремя видами спорта?
Сколько ребят увлекается лишь одним из этих видов спорта?
-баскетболисты
- хоккеисты
- футболисты
-ничем
-общая часть кругов Б, Х и Ф
изображает ребят,
увлекающихся тремя видами
спорта

19.

аскетболом
оккеем
утболом
занимаются:
Составляем уравнение, пользуясь тем, что класс разбился на
отдельные группы ребят
Таким образом, двое ребят увлекаются всеми тремя видами
спорта.
Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем
количество ребят, увлекающихся лишь одним видом спорта:
21 человек.
Ответ:
Двое ребят увлекаются всеми тремя видами спорта.
Увлекающихся лишь одним видом спорта: 21 человек.

20.

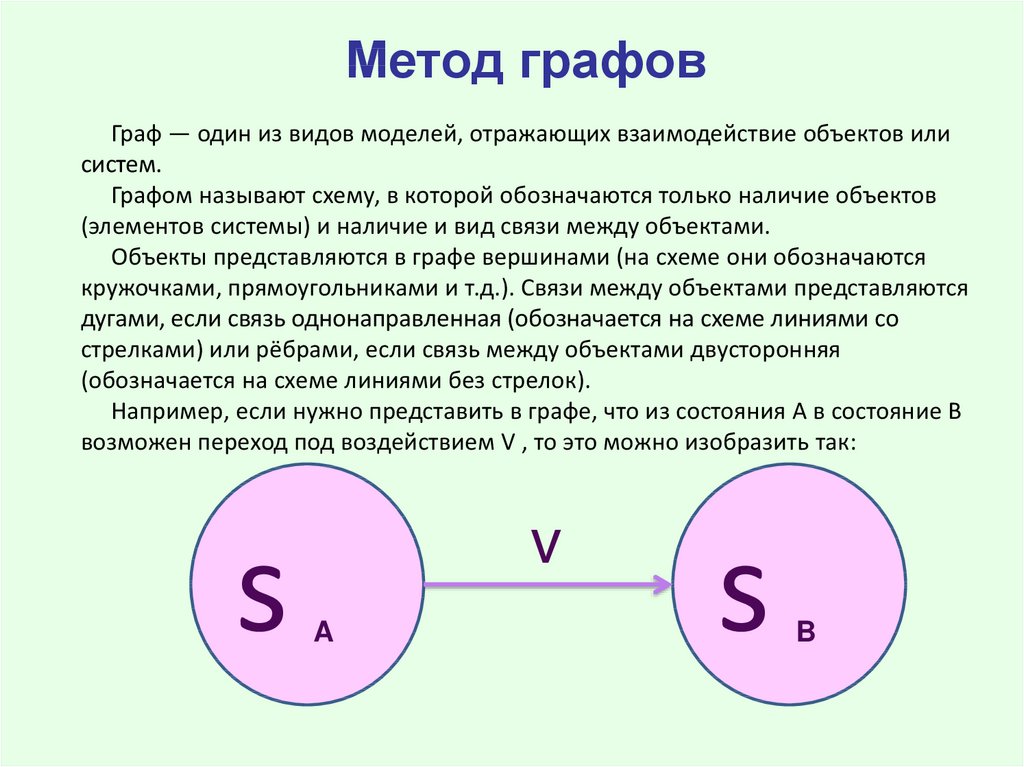
Метод графов
Граф — один из видов моделей, отражающих взаимодействие объектов или
систем.
Графом называют схему, в которой обозначаются только наличие объектов
(элементов системы) и наличие и вид связи между объектами.
Объекты представляются в графе вершинами (на схеме они обозначаются
кружочками, прямоугольниками и т.д.). Связи между объектами представляются
дугами, если связь однонаправленная (обозначается на схеме линиями со
стрелками) или рёбрами, если связь между объектами двусторонняя
(обозначается на схеме линиями без стрелок).
Например, если нужно представить в графе, что из состояния А в состояние В
возможен переход под воздействием V , то это можно изобразить так:
s
v
A
s
B

21.

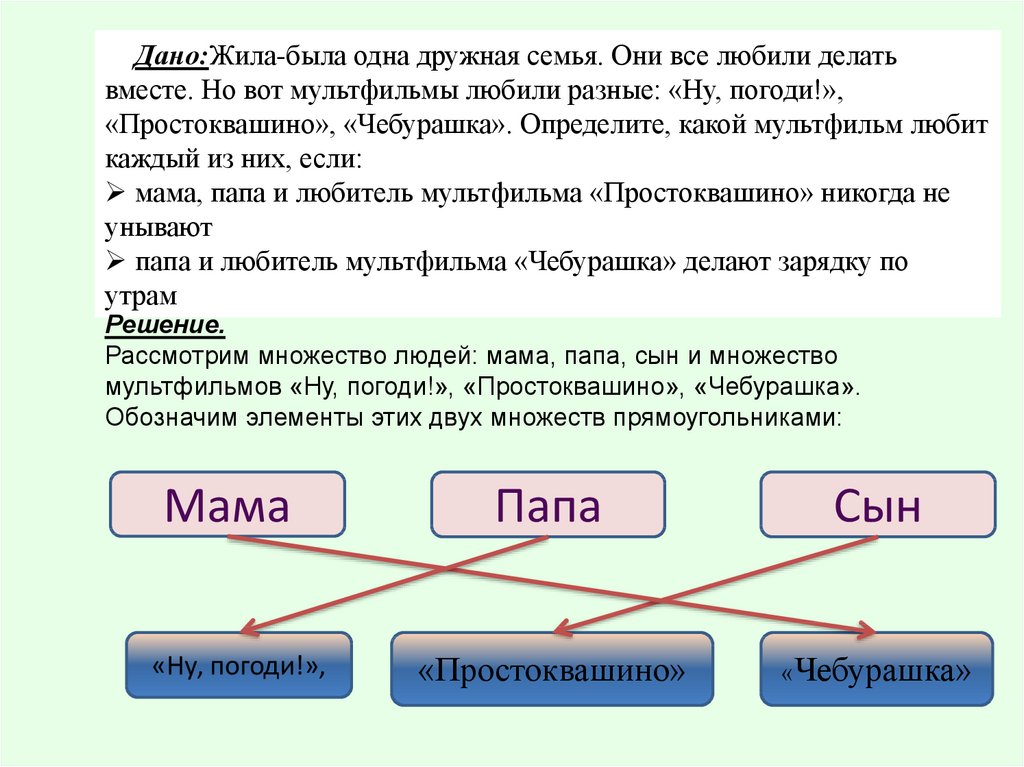
Дано:Жила-была одна дружная семья. Они все любили делать
вместе. Но вот мультфильмы любили разные: «Ну, погоди!»,
«Простоквашино», «Чебурашка». Определите, какой мультфильм любит
каждый из них, если:
мама, папа и любитель мультфильма «Простоквашино» никогда не
унывают
папа и любитель мультфильма «Чебурашка» делают зарядку по
утрам
Решение.
Рассмотрим множество людей: мама, папа, сын и множество
мультфильмов «Ну, погоди!», «Простоквашино», «Чебурашка».
Обозначим элементы этих двух множеств прямоугольниками:
Мама
«Ну, погоди!»,
Папа
Сын
«Простоквашино»
«Чебурашка»

22.

Задачи, решённые с
помощью таблиц
Сначала приговор, потом
доказательство.
Л.Керролл
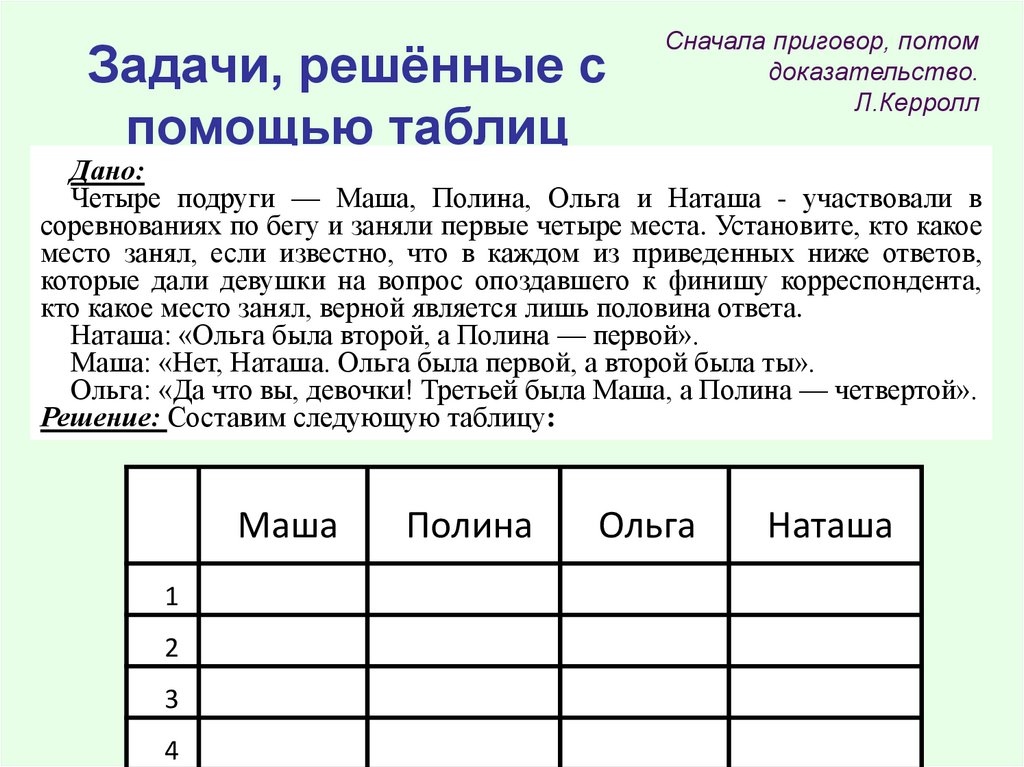
Дано:
Четыре подруги — Маша, Полина, Ольга и Наташа - участвовали в
соревнованиях по бегу и заняли первые четыре места. Установите, кто какое
место занял, если известно, что в каждом из приведенных ниже ответов,
которые дали девушки на вопрос опоздавшего к финишу корреспондента,
кто какое место занял, верной является лишь половина ответа.
Наташа: «Ольга была второй, а Полина — первой».
Маша: «Нет, Наташа. Ольга была первой, а второй была ты».
Ольга: «Да что вы, девочки! Третьей была Маша, а Полина — четвертой».
Решение: Составим следующую таблицу:
Маша
1
2
3
4
Полина
Ольга
Наташа

23.

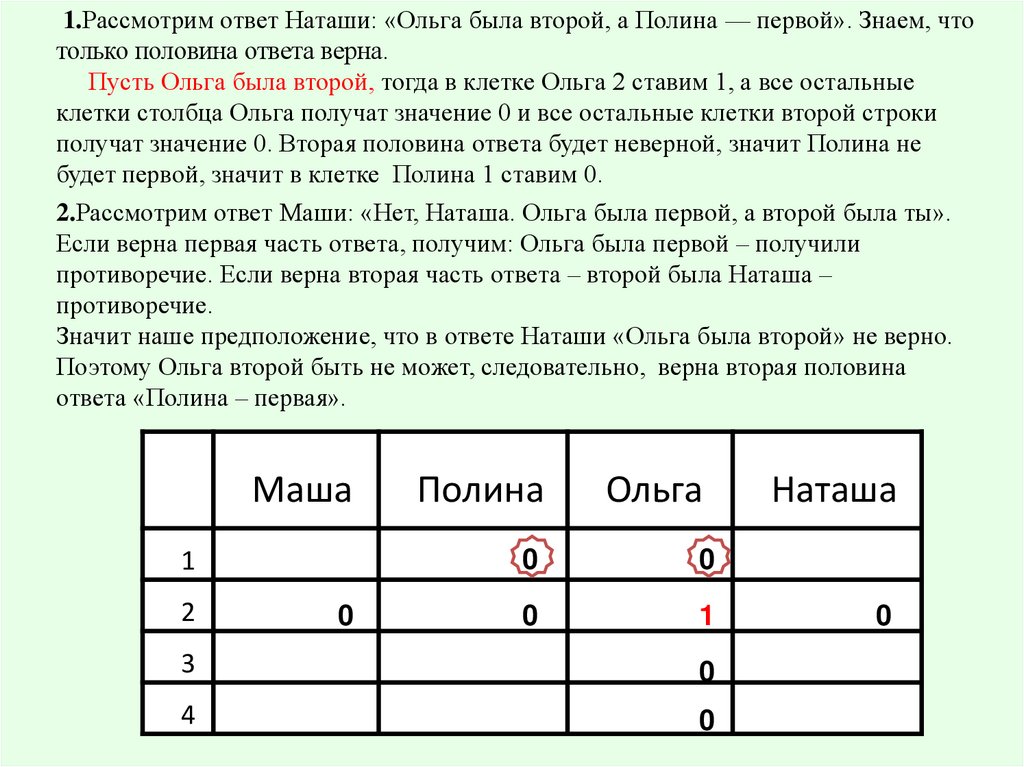
1.Рассмотрим ответ Наташи: «Ольга была второй, а Полина — первой». Знаем, что
только половина ответа верна.
Пусть Ольга была второй, тогда в клетке Ольга 2 ставим 1, а все остальные
клетки столбца Ольга получат значение 0 и все остальные клетки второй строки
получат значение 0. Вторая половина ответа будет неверной, значит Полина не
будет первой, значит в клетке Полина 1 ставим 0.
2.Рассмотрим ответ Маши: «Нет, Наташа. Ольга была первой, а второй была ты».
Если верна первая часть ответа, получим: Ольга была первой – получили
противоречие. Если верна вторая часть ответа – второй была Наташа –
противоречие.
Значит наше предположение, что в ответе Наташи «Ольга была второй» не верно.
Поэтому Ольга второй быть не может, следовательно, верна вторая половина
ответа «Полина – первая».
Маша
1
2
0
Полина
Ольга
0
0
0
1
3
0
4
0
Наташа
0

24.

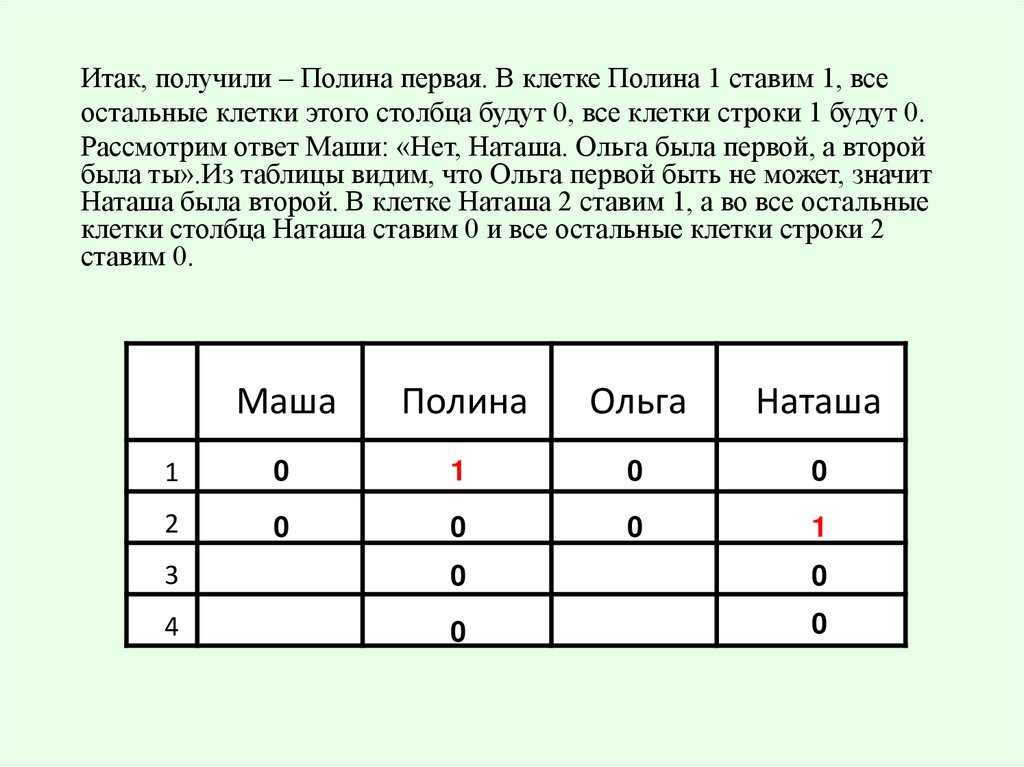
Итак, получили – Полина первая. В клетке Полина 1 ставим 1, все
остальные клетки этого столбца будут 0, все клетки строки 1 будут 0.
Рассмотрим ответ Маши: «Нет, Наташа. Ольга была первой, а второй
была ты».Из таблицы видим, что Ольга первой быть не может, значит
Наташа была второй. В клетке Наташа 2 ставим 1, а во все остальные
клетки столбца Наташа ставим 0 и все остальные клетки строки 2
ставим 0.
Маша
Полина
Ольга
Наташа
1
0
1
0
0
2
0
0
0
1
3
0
0
4
0
0

25.

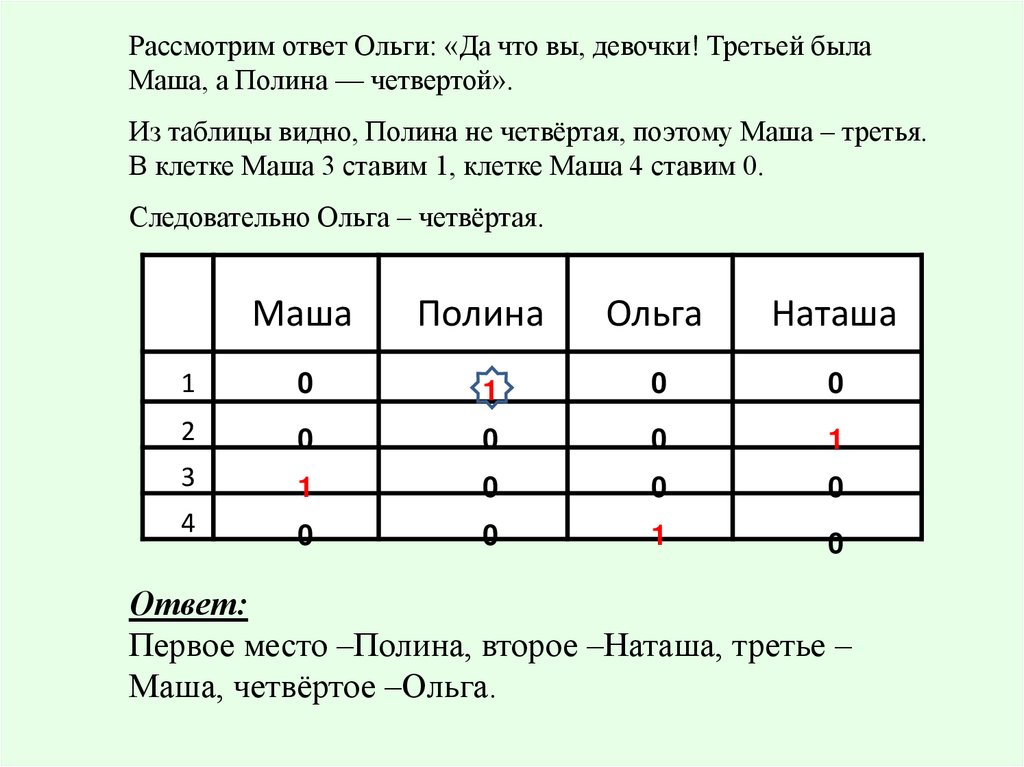
Рассмотрим ответ Ольги: «Да что вы, девочки! Третьей была
Маша, а Полина — четвертой».
Из таблицы видно, Полина не четвёртая, поэтому Маша – третья.
В клетке Маша 3 ставим 1, клетке Маша 4 ставим 0.
Следовательно Ольга – четвёртая.
Маша
Полина
Ольга
Наташа
1
0
1
0
0
2
0
0
0
1
3
1
0
0
0
4
0
0
1
0
Ответ:
Первое место –Полина, второе –Наташа, третье –
Маша, четвёртое –Ольга.

26.

Решение задач методом
бильярдного стола.
Прежде чем решать задачу, подумай, что
делать с ее решением!
Д.Пойа
Подобно тому как азартная игра в кости вызвала к жизни «исчисление»
вероятностей, игра в бильярд послужила предметом серьёзных научных
исследований по механике и математике.
Известны различные варианты игры на бильярде. Например, так
называемый французский бильярд вообще не имеет луз (при игре во
французский бильярд нужно попасть в заданный шар после нескольких
столкновений с другими шарами). Французский бильярд и послужил
прообразом математического бильярда.
Бильярдом в четырёхугольнике называется система: один точечный
бильярдный шар на четырёхугольном столе без луз, движущейся по нему
без трения и отражающийся от его сторон («бортов») по бильярдному
закону «угол падения равен углу отражения».
Данный метод применим в основном к задачам, где требуется отлить
какую-либо часть воды из наполненного сосуда данной емкости при
помощи двух других пустых сосудов тоже известной емкости.
В качестве примера подробно рассмотрим одну задачу.

27.

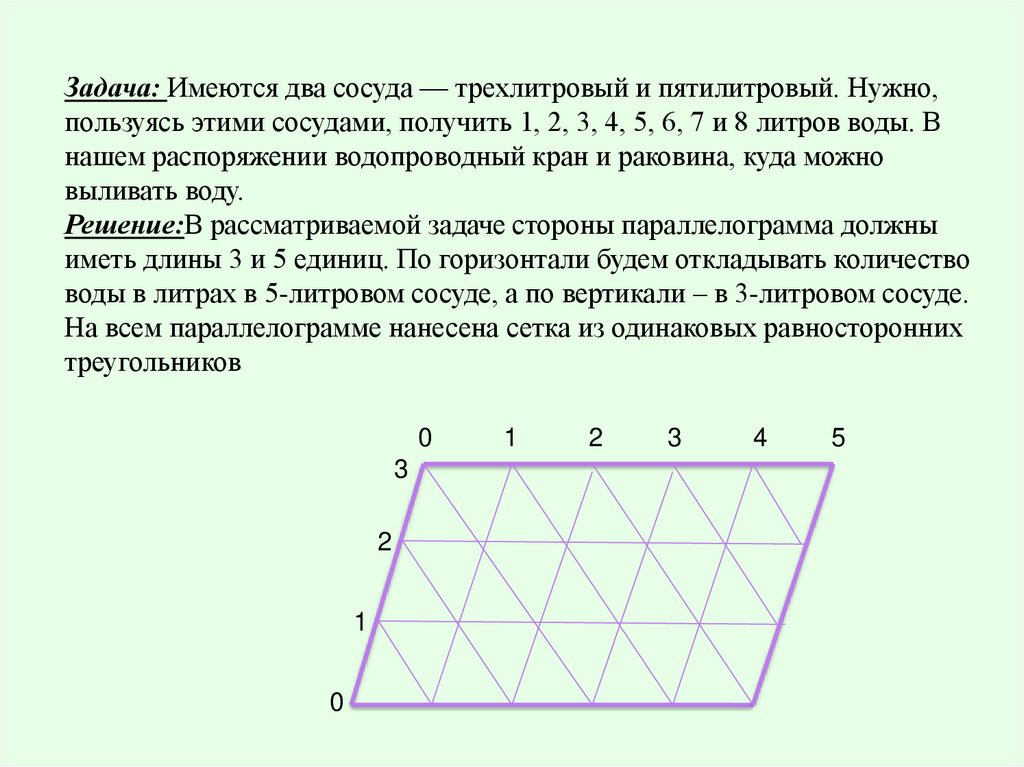
Задача: Имеются два сосуда — трехлитровый и пятилитровый. Нужно,
пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В
нашем распоряжении водопроводный кран и раковина, куда можно
выливать воду.
Решение:В рассматриваемой задаче стороны параллелограмма должны
иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество
воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде.
На всем параллелограмме нанесена сетка из одинаковых равносторонних
треугольников
0
3
2
1
0
1
2
3
4
5

28.

Бильярдный шар может перемещаться только вдоль прямых,
образующих сетку на параллелограмме. После удара о стороны
параллелограмма шар отражается и продолжает движение вдоль
выходящего из точки борта, где произошло соударение. При этом каждая
точка параллелограмма, в которой происходит соударение, полностью
характеризует, сколько воды находится в каждом из сосудов.
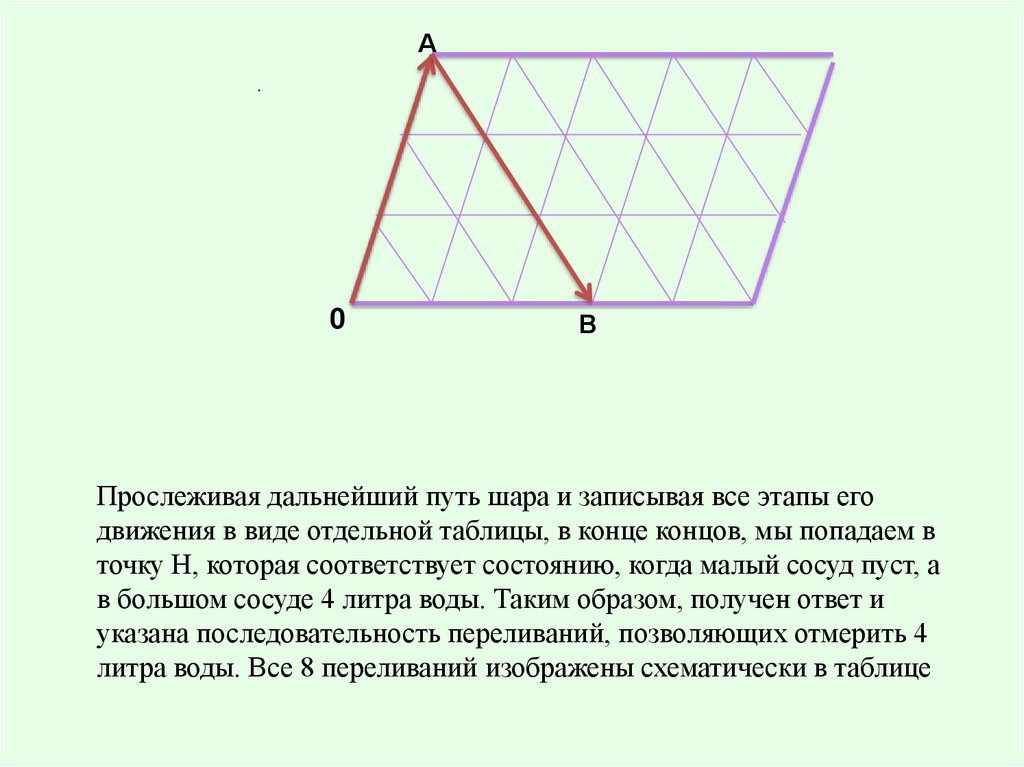
Пусть шар находится в левом нижнем углу и после удара начнет
перемещаться вверх вдоль левой боковой стороны параллелограмма до
тех пор, пока не достигнет верхней стороны в точке А. Это означает, что
мы полностью наполнили водой малый сосуд. Отразившись упруго, шар
покатится вправо вниз и ударится о нижний борт в точке В, координаты
которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом
сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду
из малого сосуда в большой сосуд.

29. Прослеживая дальнейший путь шара и записывая все этапы его движения в виде отдельной таблицы, в конце концов, мы попадаем в

А
.
0
В
Прослеживая дальнейший путь шара и записывая все этапы его
движения в виде отдельной таблицы, в конце концов, мы попадаем в
точку Н, которая соответствует состоянию, когда малый сосуд пуст, а
в большом сосуде 4 литра воды. Таким образом, получен ответ и
указана последовательность переливаний, позволяющих отмерить 4
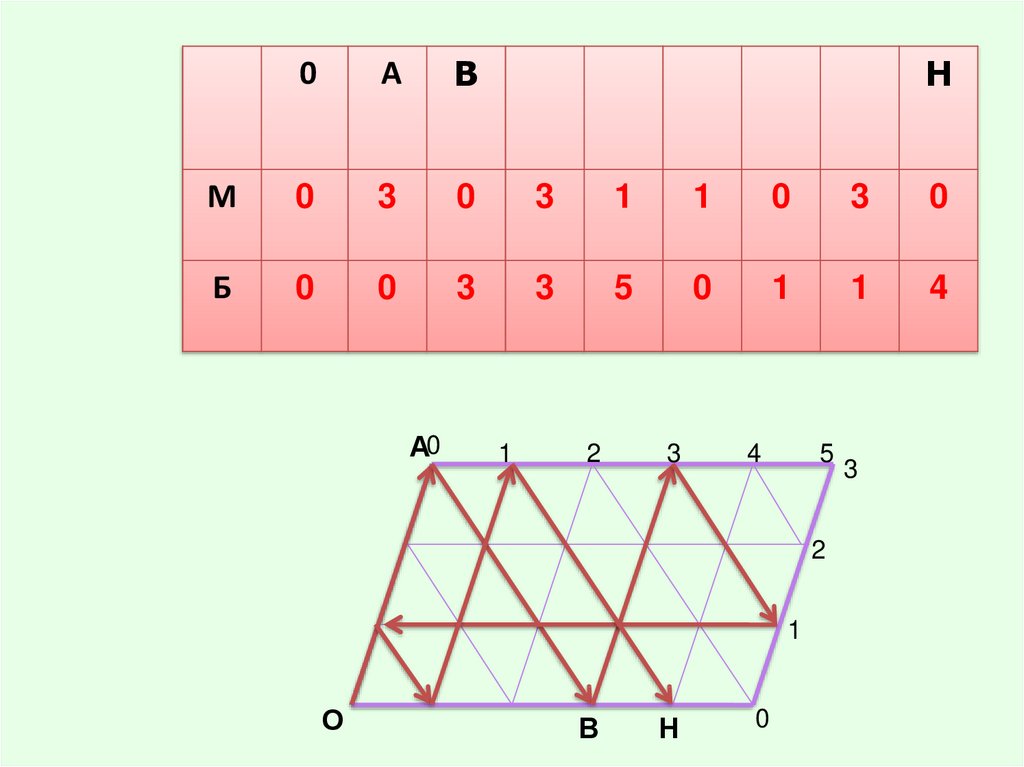
литра воды. Все 8 переливаний изображены схематически в таблице

30.

0
А
В
М
0
3
0
3
1
1
0
3
0
Б
0
0
3
3
5
0
1
1
4
А0
Н
1
2
3
4
5
2
1
О
В
Н
0
3