Similar presentations:
Степенная функция
1.
6.4. Степенная функцияИ зучи м отоб раж ен и е, осущ ествляем ое степ ен н ой ф ун кц и ей
w z n , г д е n , n 1 .
Ф у н к ц и я w z n о п р е д е л е н а н а D . Д о о п р е д е л и м е е в т . z ,
п о л о ж и в w = .
2.
Ф ун кц и я w z n и м еет п рои звод н ую в лю б ой т. z : w / nzn 1
,
w / 0 при z 0 . П оэтом у, отображ ение, осущ ествляем ое этой
ф ункцией конф орм но. О на отображ ает расш и ренную плоскость
( z ) н а р а с ш и р е н н у ю п л о с к о с т ь ( w ).
3.
Э та ф ункция не является однолистной, всякая т. w , отличная отн уля и б ескон ечн ости и м еет ровн о n п рооб р азов, сод ерж ащ и хся
в ф орм уле
n
w
n
a rg w 2 k
a rg w 2 k
w cos
i s in
n
n
k 0 , n 1.
И т а к , о т о б р а ж е н и е w z n н е я в л я е т с я в за и м н о -о д н о з н а ч н ы м .
4.
В ы ясн им , сохран яю тся ли углы в т. z 0 и z п рио то б р аж ен и и w z n.
П усть - кривая, вы ходящ ая из т. z 0, касательная к
ко то ро й н акл он ен а п о д угл ом к о си 0 х.
5.
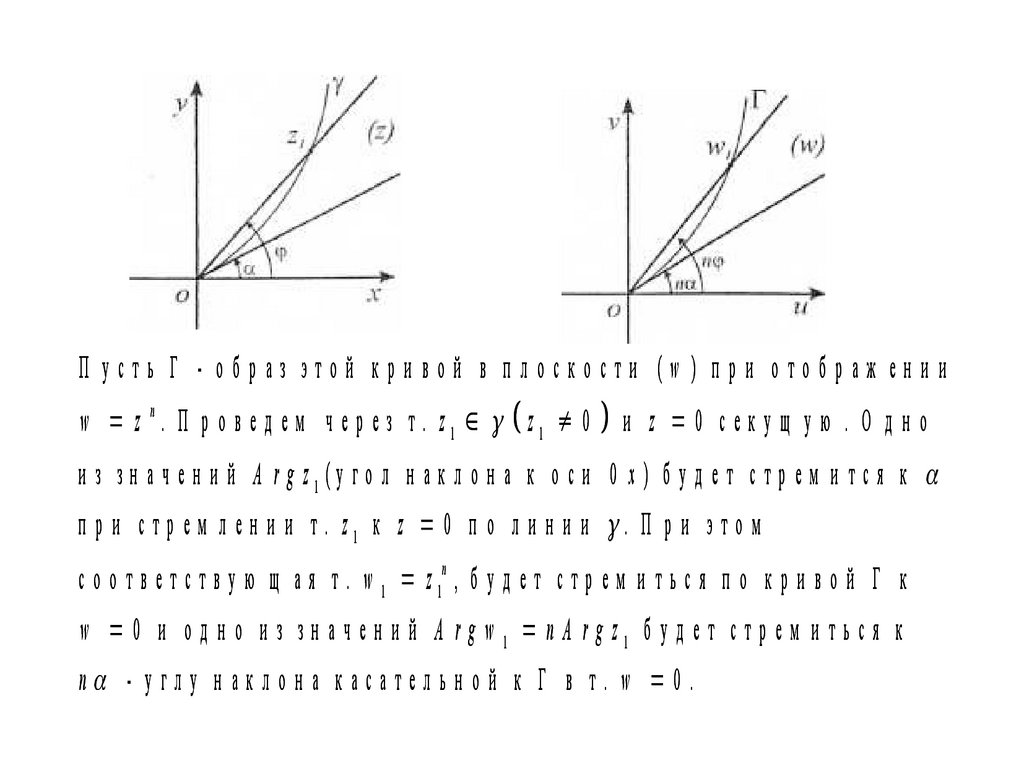
П усть Г - образ этой кри вой в п лоскости (w ) п ри отображ ен и иw z n. П р о в е д е м ч е р е з т . z1 z1 0
и z 0 секущ ую . О дно
и з зн а ч е н и й A rg z1(у го л н а к л о н а к о с и 0 x ) б у д е т с т р е м и т с я к
п р и с т р е м л е н и и т . z1 к z 0 п о л и н и и . П р и э т о м
с о о т в е т с т в у ю щ а я т . w 1 z 1n , б у д е т с т р е м и т ь с я п о к р и в о й Г к
w 0 и о д н о и з зн а ч е н и й A rg w 1 n A rg z1 б у д е т с т р е м и т ь с я к
n - угл у н ак л о н а к асател ьн о й к Г в т. w 0 .
6.
П у с т ь т е п е р ь и з т . z 0 в ы х о д я т к р и в ы е 1 и 2 , к а с а т е л ь н ы е кк о то р ы м о б р азую т с о сью О х угл ы 1 и 2. Т о гд а уго л м еж д у
1 и 2 в т . z 0 р а в е н = 2 1. О б р а з ы э т и х к р и в ы х - Г 1 , Г
2
отоб раж ен и и w z n об р азую т с осью O v углы соответствен н о
n 1 и n 2. П о это м у уго л м еж д у Г 1 и Г 2 в т. w 0 р ав е н
n 2 n 1 n 2 1 n . И т а к , о т о б р а ж е н и е w z n в т . z 0
увели чи вает углы в n раз.
при
7.
П окаж ем теп ерь, что в т. z углы тож е увел и чи ваю тся в n раз.П усть L 1 и L2 - кри вы е, угол м еж ду которы м и в т. z равен .
Э то озн ачает п о оп ред елен и ю угла в т. z , что об разы кри вы х
1
L 1 и L 2 п р и о т о б р а ж е н и и к р и в ы е l1 и l 2 о б р а з у ю т в т . 0
z
у г о л . С д р у г о й с т о р о н ы у г о л м е ж д у к р и в ы м и L 1/ и L /2 ( о б р а з а м и
кривы х L
1
и L2 п ри отоб раж ен и и w zn) в т. w равен углу
м е ж д у к р и в ы м и l 1 / и l 2/ в т . 0 , г д е l 1 / и l 2/ - о б р а з ы к р и в ы х L 1/ и L /2
1
при отображ ении .
w
8.
n1
1
В след стви е о чеви д н о го со о тн о ш ен и е n n кр и вы е
z
z
l 1 / и l 2/ с л у ж а т о б р а з а м и к р и в ы х l 1 и l 2 п р и о т о б р а ж е н и и n .
С л е д о в а т е л ь н о , п о д о к а з а н н о м у в ы ш е , у г о л м е ж д у l 1 / и l 2/
в т . 0 р а в е н n , о т к у д а у г о л м е ж д у L 1/ и L /2 в т . р а в е н n ,
что и треб овалось д оказать
9.
И з п рави ла возвед ен и я ком п лексн ого чи сла в степ ен ьn
n
n
n
z z (c o s п A r g z i s in n A r g z ) с л е д у е т д л я w z : w z ,
A rgw nA rgz.
О тсю да видно, что ф ункция w zn отображ ает луч
A rg z 0 2 k , вы х о д ящ и й и з т. z 0 п о д угл о м 0 к
п о л о ж и тел ьн о м у н ап р авл ен и ю о си О х, н а л уч A rg w п 0 2 k ,
в ы х о д ящ и й и з т. w 0 п о д угл о м n 0 к п о л о ж и тел ьн о м у
направлению оси О u.
10.
О круж ность z r центром в начале координат и радиуса rотображ ается ф ункцией w zn на окруж ность w rn с ц ентром
в т. w 0 р ад и усо м r n. К о гд а т. z о д и н р аз о п и сы вает о кр уж н о сть
в п о л о ж и т е л ь н о м н а п р а в л е н и и (а р гу м е н т н е п р е р ы в н о в о зр а с т а я
увеличивается на 2 ) точка w zn обеж ит n раз окруж ность
w r n (а р гу м е н т н е п р е р ы в н о в о зр а с т а я у в е л и ч и т с я н а 2 n ).
11.
Ф ункция w zn не является однолистной, но для нее м ож новы делить область однолистности. Т аковой является
2
вн утрен н ость лю бого угла с цен тром в т. z 0 раствором
.
n
П ростей ш ей такой об ластью является вн утрен н ость угла D с
2
верш иной в т. z 0 :
.
n
12.
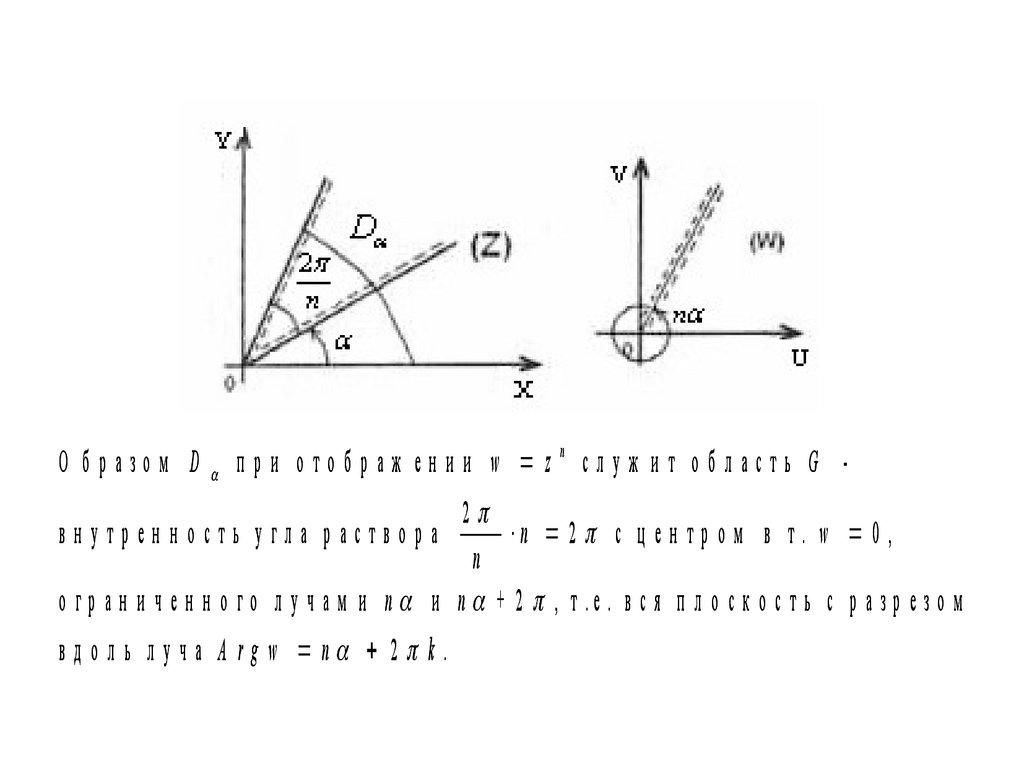
О б р азо м Dпри отображ ении w zn служ ит область G -
2
внутрен н ость угла раствора
n 2 с ц е н т р о м в т . w 0 ,
n
о г р а н и ч е н н о г о л у ч а м и n и n + 2 , т .е . в с я п л о с к о с т ь с р а з р е з о м
вд о л ь л уч а A rg w n 2 k .
13.
Т ак как w zn однолистна в D , то она отображ ает Dод н озн ачн о и кон ф орм н о н а п лоскость
л уч а A rg w n 2 k .
w
взаи м н о
с р азрезом вд оль
14.
П ри м ер. О тоб рази м взаи м н о од н озн ачн о и к он ф орм н овн утрен н ость угла D .
a rg z
на верхню ю полуплоскость.
4
4
15.
Т ак как D угол раствора, а полуп лоскость угол раствора ,
2
то прим еняя отображ ение z2, переводим D в п олуплоскость
D 1 : a rg z .
2
2
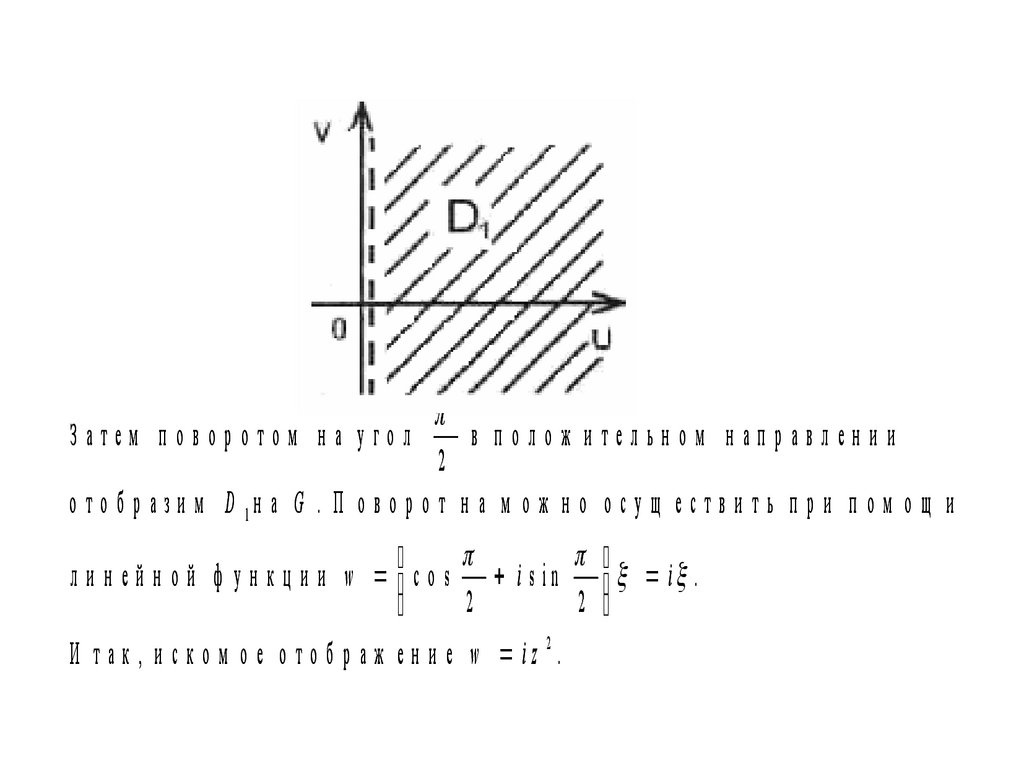
И зо б р ази те D 1!
16.
Затем п оворотом н а уголв полож ительном направлении
2
о т о б р а з и м D 1н а G . П о в о р о т н а м о ж н о о с у щ е с т в и т ь п р и п о м о щ и
л и н е й н о й ф у н к ц и и w c o s i s i n i .
2
2
И т а к , и с к о м о е о т о б р а ж е н и е w iz 2.
17.
6 .5 . Ф у н к ц и я wn
z . П он я ти е м н огозн ач н ой
ф ун к ц и и . В ы дел ен и е одн озн ач н ы х в етв ей
Р ассм отрим в плоскости
z
2
с верш иной
n
z 0, огран и чен н ой лучам и
2
A rgz 2 k и A rgz
2 m ,
n
k , m .
угол D раствором
Т о гд а ф ун кц и я w z n о то б р ази т
вн утрен н о сть угл а D взаи м н о
о д н озн ачн о и кон ф орм н о н а об ласть
G - плоскость
w
с р азрезом вд о ль
л уч а A rg w 2 l,l Z .
18.
Я вляется ли w zn одн оли стн ой в D ? Е сли да, что и з этогоследует?
19.
В об ласти D ф ун кц и я w z n од н оли стн а, об разом D п ри этомотображ ении является область G . С ледовательно для ф ункции
w zn, определенной в области D , сущ ествует обратная
ф ункция, определенная в области G и им ею щ ая м нож еством
зн ач ен и й о б л асть D .
О б озн ачи м эту об ратн ую ф ун кц и ю z
я в л я е т с я а н а л и т и ч е с к о й в G . |П о ч е м у ?
w . Э та ф ункция
n
1
20.
К ак обратн ая ан али тической ф ункц и и w zn, D .П р о и з в о д н а я о т э т о й о б р а т н о й в ы ч и с л я е т с я п о ф о р м у л е ...? ...
21.
dw
n
dw
1
1
z
n
/
1
nz
n 1
1
n
n
w1
n 1
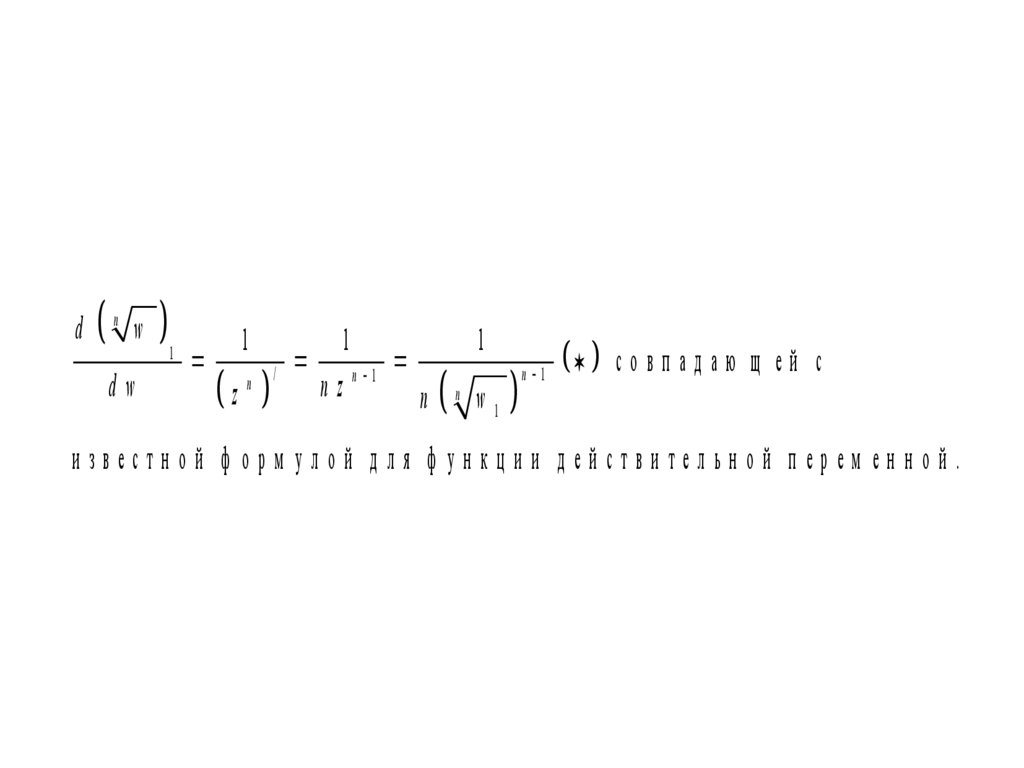
совпадаю щ ей с
и звестн ой ф орм улой д ля ф ун кц и и д ей стви тельн ой п ерем ен н ой .
22.
Д ля ф ункции w zn сущ ествую т области однолистности,отличны е от вы бранной нам и области D . В качестве области
одн оли стн ости для дан н ой ф ун кци и м ож но вы брать лю бой угол
2
(т о ч н е е е го в н у т р е н н о с т ь ) с в е р ш и н о й в т . z 0 , р а с т в о р о м
.
n
Э ти области м ож н о вы брать так, чтобы он и н е н алегая друг н а
д руга зап олн яли соб ой всю п лоскость
z .
23.
К а ж д а я и з о б л а с т е й D 1 , D 2 ,..., Dn
отображ ается при пом ощ и
ф ун кц и и w z n о д н о зн ач н о и ко н ф о р м н о н а п л о ско сть (w ) с
р азр езо м вд о л ь п о л о ж и тел ьн о й д ей стви тельн о й п о л уо си О u.
2
В сам ом д еле лю б ой луч A rg z
k 2 п, где k 0,n 1
n
2
ото б р аж ается н а л уч A rgw n
k 2 m 2 k m .
n
24.
И так, всяки й угол Dk
ф ун кц и я w z n отоб раж ает взаи м н о
од н озн ачн о и ком ф орм н о н а од н у и ту ж е о б ласть G
п л о с к о с т ь w
с р азр езо м вд ол ь п о ло ж и тел ьн о й
действительной оси. С оответствие, обратн ое соответствию
D k G , о п р ед ел яет о д н о зн ач н ую ф ун кц и ю , о б ратн ую к w z n,
которую об озн ачи м z
w
n
k
. Э та ф ункция отображ ает G на D k.
25.
Е сли W и зм ен яется в об ласти G , то z м ож н о счи татьи з м е н я ю щ и м с я в л ю б о й и з о б л а с т е й D 1 , D 2 ,..., D n , б л а г о д а р я
чем у м ож н о говори ть н е об од н ой , а об n о б ратн ы х ф ун кц и ях
для ф ункции w zn определенны х в области G , и им ею щ их
м н о ж е с т в о з н а ч е н и й с о о т в е т с т в е н н о в о б л а с т и D 1 , D 2 ,..., D n .
М нож ество всех этих обратны х м ож но рассм атривать как
м н огозн ачн ую ф ун кц и ю , об ратн ую к ф ун кц и и w zn, которую
б уд ем об озн ачать z n w .
26.
К аж дую из обратны х ф ункций для ф ункции w znрассм атри ваю т как од н озн ачн ую ветвь м н огозн ачн ой ф ун кц и и
z n w . Ф у н к ц и я z n w и м е е т n в е т в е й , э т о n -зн а ч н а я ф у н к ц и я .
Ч т о б ы ф и к с и р о в а т ь к а к у ю -л и б о и з в е т в е й д о с т а т о ч н о л и ш ь
указать в како й о б л асти и зм ен яется z. В со о тветстви и с
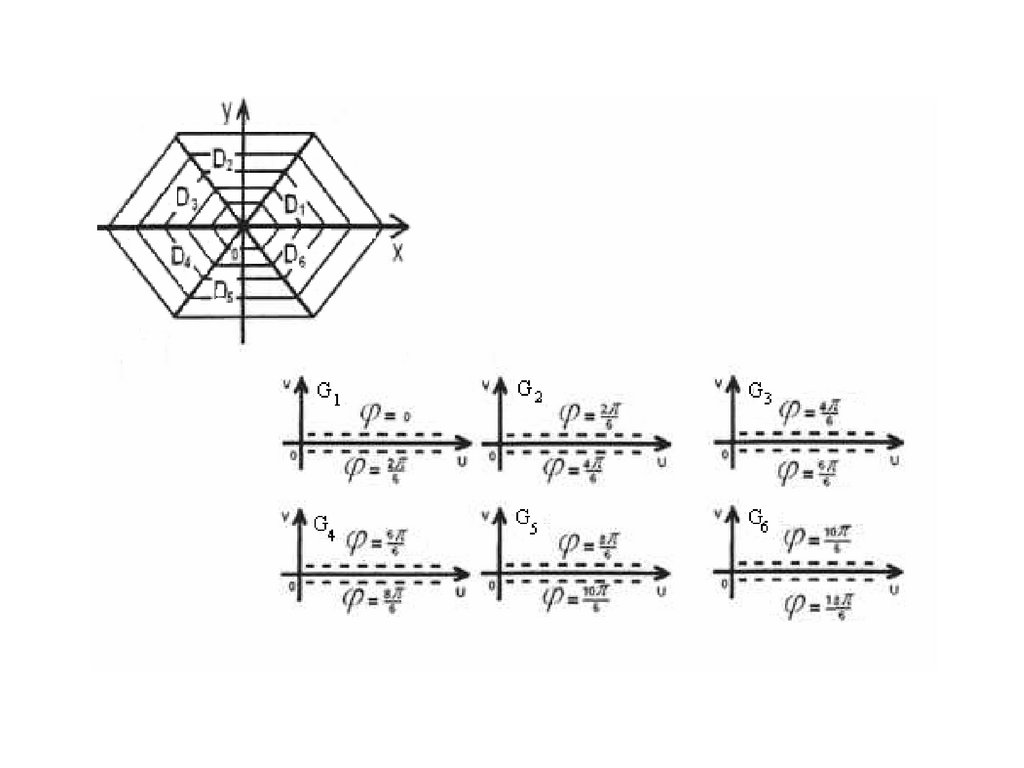
об озн ачен и ям и н а ри с. 1 б уд ем п ользоваться след ую щ и м и
об озн ачен и ям и д ля од н озн ачн ы х ветвей ф ун кц и и z n w :
n
w
1
,
n
w
2
,...,
w
n
n
.
27.
Зам ечание 1. Н еобходим о им еть в виду, что понятие ветвитесн о связан о с оп ред елен н ы м вы б ором об л асти од н оли стн ости .
Т ак, м ож но бы ло бы вы брать области однолистности
с л е д у ю щ и м о б р а з о м : 0 , 1 ,..., n 1 , г д е k - у г о л с в е р ш и н о й в
2 k
2 k
т. z 0, о гран и чен н ы й лучам и : A rgz
, A rgz
,
n
n
n
n
где k 0,n 1
28.
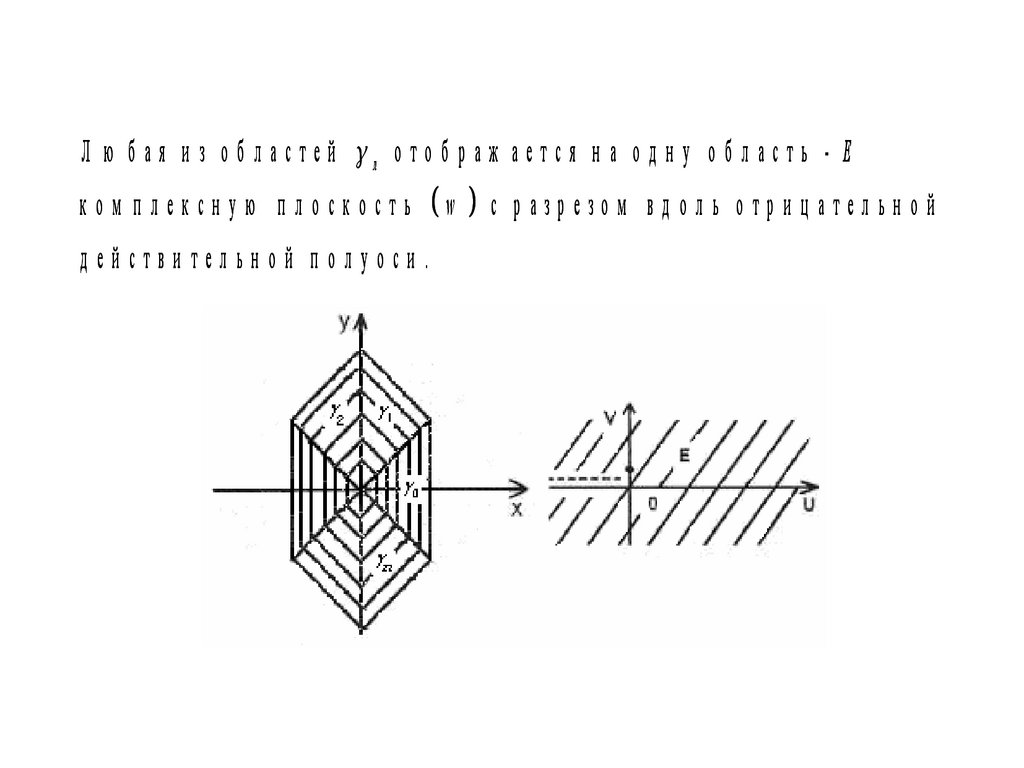
Л ю б ая и з об ластей л отоб раж ается н а од н у об ласть - Еком плексную плоскость
действительной полуоси.
w
с р азр езо м вд ол ь о три ц ател ьн о й
29.
В с а м о м д е л е , к о г д а т . z z e i a rg z о п и с ы в а е т л у ч a r g z c o n s t ,т о т . w z n e in a rg z о п и с ы в а е т л у ч a r g z n c o n s t .И е с л и
2 k
2 k
м еняется от
до
, т о л у ч a rg z в р а щ а я с ь
n
n
n
n
п р о ти в ч асо в о й стр ел к и п р о б е гает в сю о б л асть k , в то в р ем я
к а к с о о т в е т с т в у ю щ и й е м у л у ч a rg w n в р а щ а я с ь п р о т и в
часовой стрелки от луча A rgw 2 k д о луча
A rg w 2 k п ро б егает всю о б ласть Е .
30.
В области Е тож е м ож ет бы ть определена ф ункция, обратнаяф ун кц и и w z n, п р и том n разли чн ы м и сп о со б ам и со об разн о
n р а з л и ч н ы м о б л а с т я м 0 , 1 , ..., n 1. И н ы м и с л о в а м и в о б л а с т и Е
м огут бы ть оп ределен ы n ветвей ф ун кци и z n w .
Е сл и заф и к си р о в ат ь о д н у и з о б л аст ей n, м ы п о л у ч и м о д н у и з
ветвей ф ункции z n w .
31.
П р и эт о м , е с л и W л е ж и т в в е р х н е й п о л у п л о с к о с т и 0 a rg w ,т о ч к а z л е ж и т в н у т р и у г л а 0 a r g z , т .е . в ч а с т и п л о с к о с т и
n
п р и н а д л е ж а щ е й к а к о б л а с т и D 1, т а к и о б л а с т и 0. Е с л и w л е ж и т
в н и ж н е й п о л у п л о с к о с т и ( a rg z 0 ), т о z л е ж и т в н у т р и у гл а
a rg z 0 , т .е . ч а с т и z п л о с к о с т и , п р и н а д л е ж и т к а к
n
о б л а с т и 0 , т а к и о б л а с т и D n.
Ч то это зн ачи т?
32.
Э то зн ачи т, что рассм атри ваем ая н ам и ветвь ф ун кц и и z n w вверхней полуплоскости совпадает с ранее определенной ветвью
z
w , а в ниж ней
n
1
ветвью , а им енно z
п олуп лоскости буд ет совп ад ать с д ругой
w
n
n
. И так, бы ло бы неправильно
р ассм атр и вать ветви о д н ой и то й ж е м н ого зн ач н о й ф ун кц и и
как отдельны е ф ункции.
33.
В п ри вед ен н ом п ри м ере п ри и зм ен и вш ем ся вы б оре об ластиоднолистности две ветви z
w
n
1
и z
w
n
n
,
рассм атри вавш и еся сн ачала как разли чн ы е, оп ред еляю т од н у и
ту ж е ветвь.
34.
П ом ен яв ролям и z и w м н огозн ачн ую ф ун кц и ю , об ратн ую кстеп ен н ой w zn зап и ш ем ви д е w
n
z.
35.
П р и м е р 1 . П у с т ь n 2 и G -п л о с к о с т ь ( z ) с р а з р е з о м в д о л ьотрицательной части действительной оси.
Э том у случаю соответствует разб и ен и е п ло скости
w
на две
полуплоскости D 1 :R e w 0 и D 2 :R e w 0.
В етвь
z
D
2
1
z , отображ аю щ ая G на D 1 есть
есть
a rg z
a rg z
z cos
i s in
, а ветвь, отоб раж аю щ ая G н а
2
2
a rg z 2
a rg z 2
z z c o s
i s in
.
2
2
2
36.
Зам ечан и е 2. В си лу того, что области Dт о ч е к п р и k j, о б л а с т ь D
k
k
и D
j
не им ею т общ их
о п р е д е л я е т с я за д а н и е м к а к о й -л и б о
одной точки w 0, ей принадлеж ащ ей. П оэтом у, чтобы вы делить
од н озн ачн ую ветвь
n
z в д ан н о й о б л асти G , д о стато ч н о зад ать
в к а к о й -л и б о о д н о й т о -ч к е z 0 G з н а ч е н и е
n
z0 w 0.
37.
П р и м ер 2 . В п л о скости (z) с р азр езо м вд ол ь отр и ц ател ьн о йч а с т и д е й с т в и т е л ь н о й о с и (о б л а с т ь G ) в ы д е л и м в е т в ь
3
z,
к о т о р а я в т . z 0 1, п р и н и м а е т з н а ч е н и е w 0 1 . З д е с ь о б л а с т и D 1,
D 2, D
3
н а которы е отоб раж аю т G разли чн ы е ветви
2 k
2 k
a rg w
.
3
3
3
3
3
z есть D k:
38.
О ч е в и д н о , w 0 1 п р и н а д л е ж и т D , и в е т в ь3
z есть
a rg z
a rg z
z : z z cos
i s in
.
1
1
3
3
O н a отоб раж ает G взаи м н о од н озн ачн о и кон ф орм н о н а
область D1 :
a rg z .
3
3
3
3
3
39.
6 .6 .П о н я т и е р и м а н о в о й п о в е р х н о с т иС о о т в е т с т в и е м е ж д у п л о с к о с т я м и ( z ) и ( w ), у с т а н а в л и в а е м о е
ф ун кц и ям и w z n н е является взаи м н о о д н о зн ач н ы м . Д л я
восстан овлен и я взаи м н ой од н озн ачн ости , след ует
взять n экзем п л яр о в
л и с т о в
п л о ско сти (w ) с р азр езо м вд о л ь
п о л о ж и т е л ь н о й д е й с т в и т е л ь н о й п о л у о с и O v и п о с т а в и т ь к -т ы й
экзем п ляр G k в соответстви е с углом D k.
40.
41.
2 kП р и э т о м л у ч у a rg z
, будет соответствовать ниж ний
n
р а зр е з к -т о г о л и с т а п л о с к о с т и ( w ) и в е р х н и й к р а й р а зр е за k 1
листа.
Д л я восстан о вл ен и я о д н о зн ач н о сти со о тветстви я и х н ео б хо д и м о
соединить, или, как говорят склеить.
42.
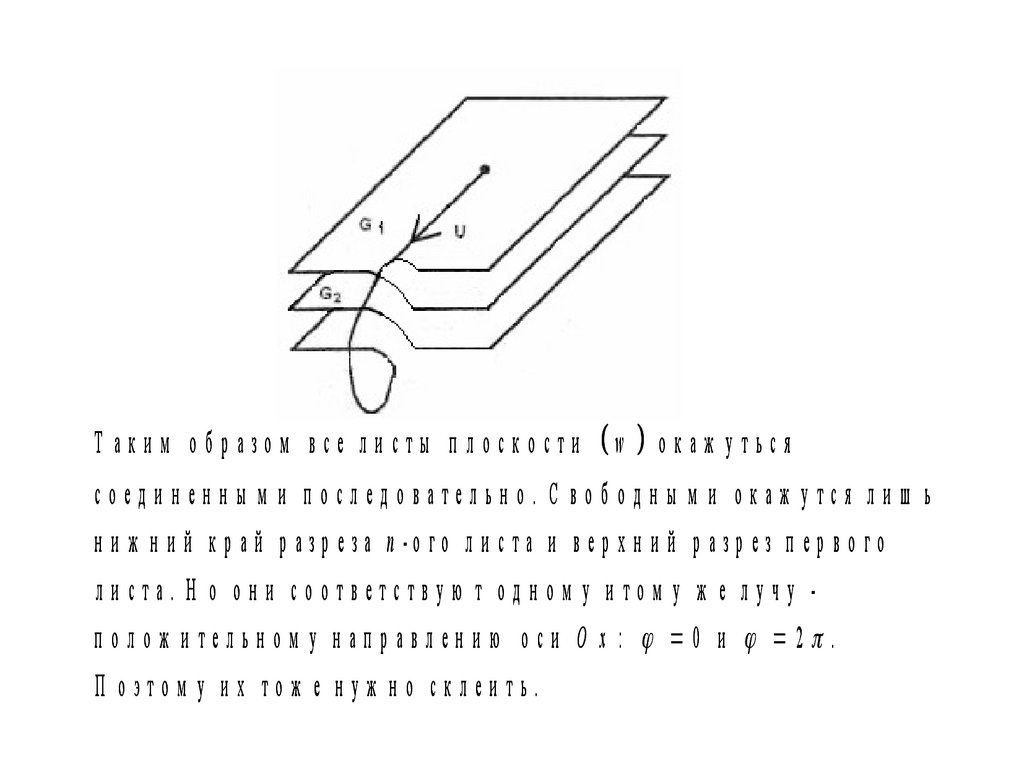
Т аки м о б р азо м все л и сты п л о ско стиw
окаж уться
соединенны м и последовательно. С вободны м и окаж утся лиш ь
н и ж н и й к р а й р а зр е за n -о г о л и с т а и в е р х н и й р а зр е з п е р в о г о
листа. Н о они соответствую т одном у итом у ж е лучу полож ительном у направлению оси О х : 0 и 2 .
П оэтом у их тож е нуж но склеить.
43.
П олучен н ая п оверхн ость н азы вается п оверх н остью Р и м ан а.Ф ункция w zn отображ ает плоскость
z
на поверхность
Р и м ан а взаи н о од н озн ачн о.
Зам ечан и е. Б . Р и м ан стал вп ервы е рассм атри вать м н огозн ачн ы е
аналитические ф ункции ком плексной перем енной на
м н оли стн ы х п оверхностях, п олучи вш и х его и м я.
44.
Зн ачен ия ф ун кц и и w zn расп олож ен ы н а n (n 2) ли стахплоскости
w
и п оэто м у н азы вается м н о го ли стн о й .
П ри склеивании листов плоскости
n
указан н ы м сп о соб о м
м ы скр еп л яем все л и сты в т. w 0 и w .
45.
Э то связан о с тем , что каж д ом у зн ачен и ю w , отли чн ом у от 0 и, соответствует n зн ачен и й z, н о w 0 соответствует
ед и н ствен н о е зн ач ен и е, z 0, a w со о тветствует z , то ч ки
w 0 и w об лад аю т особ ы м свой ством . Е сли застави ть
точку рим ановой поверхности вращ аться вокруг т. w 0, то она
будет п ереходи ть с одн ого ли ста на друго й и обой дя все n
листов, попадет в первоначальное полож ен ие
46.
Т о ж е м о ж н о сказать и о т. w . П л о ско сть н ад л еж и тпредставить в виде сф еры . В се n сф ер скреплены в верхнем и
н и ж н е м п л ю с а х .Э т и т о ч к и п р и н я т о н а з ы в а т ь т о ч к а м и
разветвлен и я ри м ан овой п оверхн ости п оряд ка
n
1 (п о
к о л и ч е с т в у л и с т о в б е з о д н о г о , т .к ., е с л и р и м а н о в а п о в е р х н о с т ь
с о с т о и т и з о д н о го л и с т а , т о н а н е й н е т т о ч е к р а зв е т л е н и я ).
47.
z6 .7 .Ф у н к ц и и e , s i n z , c o s z . Ф о р м у л ы Э й л е р а
Р ассм отрим следую щ ие три степенны х ряда:
2
3
n
z
z
z
1 z
...
... A
2! 3!
n!
3
5
7
2n 1
z
z
z
z
z
...
... B
3! 5! 7!
2 n 1 !
2
4
6
2n
z
z
z
n z
1
... 1
... C
2! 4! 6!
2 n !
48.
П окаж ем , что рядА
сходится абсолю тно во всей
ком плексн ой плоскости . С остави м ряд из м одулей его член ов
n 0
lim
n
z
n!
n
. В осп ользуем ся п ри зн аком Д алам б ера
z
n
n 1
n!
1 ! z
n
z
lim
0 1.
n n 1
С ледовательно, ряд
А
ком плексной плоскости.
абсолю тно сходится во всей
49.
А н ал о ги ч н о м о ж н о п о казать, ч то р яд ыВ
и
С
такж е
сходятся абсолю тно во всей ком плексной плоскости.
С ум м ы рядов
А , В
и
С
о б о зн ач и м со о тветствен н о чер ез
e z , s in z , c o s z . Т а к и м о б р а з о м п о о п р е д е л е н и ю :
2
3
n
z
z
z
e z 1 z
...
. . . 1
2! 3!
n!
z3 z5 z7
z 2 n 1
n 1
s in z z
... 1
... 2
3! 5! 7!
2 n 1 !
z2 z4 z6
z 2n
n
cos z
... 1
... 3
2! 4! 6!
2 n !
Г де определена каж дая из этих ф ункций?
50.
П ри чем и з сказан н ого вы ш е след ует, что к аж д ая и з ф ун кц и йе z , s in z , c o s z о п р е д е л е н а п р и л ю б о м к о м п л е к с н о м z .
З ам ети м , и з ан ал и за и звестн о , если z п р и н и м ает д ей стви тел ьн ы е
зн ачен и я х, то сум м ы ряд ов
А , В , С
суть соответственно
е x , s in x , c o s x , т о е с т ь в н о в ь в в е д е н н ы е ф у н к ц и и я в л я ю т с я ...?
51.
являю тся аналитическим продолж ением ф ункцийдей стви тельн ого п ерем ен ного на всю ком п л ексн ую п лоскость,
и б о ф у н к ц и и е z ,s in z , c o s z я в л я ю т с я а н а л и т и ч е с к и м и
ф ункциям и на всей ком плексной плоскости, так как сум м а
степ ен н ого ряд а является ан али ти ческой ф ун кц и ей вн утри
кр уга сх о д и м о сти , р ад и ус ко то р о го в д ан н о м сл уч ае р авен + .
52.
В ком п лексн ой п лоскости Э й лером устан овл ен о зам ечательн оес о о т н о ш е н и е : е iz c o s z i s i n z . 4
4
Д ля д оказательства тож д ества
зам ен и м в ряд е е z б укву z
ч е р е з iz и с о б е р е м о т д е л ь н о ч л е н ы , н е с о д е р ж а щ и е i, и ч л е н ы
с о д е р ж а щ и е i, п о л у ч и м :
iz
е 1 iz
1 iz
iz
z
2!
2!
2
2
iz
z
i
3!
3!
3
3
z
4!
iz
4!
4
4
iz
z
i
5!
5
5!
2
4
6
z
z
z
1
... i z
2
!
4
!
6
!
5
iz
6!
z
6!
z
3!
6
3
6
iz
7!
z
i
5!
...
7
...
7!
z
7
5
7
...
7!
z
53.
Зам етив, что ряд стоящ ий в первы х скобках, вы раж ает cos z, ар я д , с т о я щ и й в о в т о р ы х с к о б к а х , о п р е д е л я е т s in z , п о л у ч а е м
4 .
3 с л е д у е т ,
тож дество
И з
2
и
ч т о s in ( z ) s in z , c o s ( z ) c o s z . 5
Зам еняя в тож дестве Э йлера
4 ,
z на z, получаем :
e iz e iz
e iz e iz
s in z
, cos z
6
2i
2
Ф о р м у л ы 6 т а к ж е н о с я т и м я Э й л е р а .
54.
6 .8 Н е к о т о р ы е с в о й с т в а п о к а з а т е л ь н о й ф у н к ц и и1 . e
z
/
e
z
7
В сам ом деле,
2
3
4
2
3
z
z
z
z
z
z
e
1 z 2 ! 3 ! 4 ! ... 1 z 2 ! 3 ! ... e
Ч ем восп ользовали сь?
/
z
55.
Зд есь м ы восп ользовали сь свой ством , что всяки й степ ен н ой рядп ред ставляет соб ой ан али ти ческую ф ун кц и ю вн утри круга
сход и м ости , п ри чем п рои звод н ая от этой ф ун кц и и м ож ет б ы ть
п олучена п утем п очленн ого ди ф ф еренц и ровани я степ енн ого
ряда.
56.
2 . e a e b e a b , г д е , a , b 8П о определению :
2
3
a
a
e a 1 a
2! 3!
2
3
b
b
e b 1 b
2! 3!
Зам ечая, что ряды
перем нож ать, ибо
an
...
...
n!
bn
...
...
n!
в правой части м ож но п очленно
о н и с х о д я т с я а б с о л ю т н о , п о л у ч а е м :...?
57.
23
n
2
3
n
a
a
a
b
b
b
a
b
e e 1 a
...
... 1 b
...
...
2! 3!
n!
2! 3!
n!
a2
b2 a3 a2
a2 b3
1 a b
ab
b a
...
2! 3! 2!
2! 3!
2!
an
a n 1
a n 2
b2
bn
...
b
...
...
n!
n 2 ! 2 !
n ! n 1 !
1 a b
a
b
2!
2
a
b
3!
3
...
a
b
n!
n
... e a b
58.
3.ea
1
e
a
9
В с а м о м д е л е , п о л а г а я в ф о р м у л е 8
e a e a e a a e 0 1
b a найдем :
59.
О ткуда следует справедливость ф орм улы9
ea
4 . b e a b 1 0
e
Д ля д оказательства восп ользуем ся ф орм улам и
ea
a b
a
b
a b
e
e
e
e
eb
8
и
9 :
60.
О п ред елен и е. К о рн и уравн ен и я f (z) 0 н азы ваю тся н ул ям иф у н к ц и и f ( z ).
Т еорем а. П оказательн ая ф ун кц и я н улей н е и м еет.
В сам ом деле, ez e
e
z
x iy
e x e iy e
e x, где x R . Т ак как е
л ю б о м z .
z
x
c o s
y i s i n y . П о э т о м у
0, ибо, е
x
0, то еz 0 при
61.
6. П оказательн ая ф ун кц и я w e z является п ери о д и ческойф у н к ц и е й с п е р и о д а м и к р а т н ы м и ч и с л у 2 i.
П усть w является п ери од ом ф ун кц и и w e z, что п о оп ред елен и ю
озн ачает, что e
z w
e z д л я л ю б о г о z . Д е л я о б е ч а с т и
п о с л е д н е г о р а в е н с т в а н а е z , п о л у ч а е м : е w 1 .
П у с т ь w i . Т о г д а e i 1 , т о е с т ь е c o s i s i n .
Б еря м одули от обеих частей этого соотн о ш ен и я, п олучим , что
е 1 . Н о т а к к а к е с т ь д е й с т в и т е л ь н о е ч и с л о , т о э т о о зн а ч а е т ,
что 0.
62.
Т а к и м о б р а з о м , с у ч е т о м , ч т о е 1 и м е е м c o s i s in 1 .c o s 1,
О ткуда следует, что
Р еш ая эту систем у, получаем :
s in 0 .
2 k , k Z ,
n , n Z .
Т о есть 2 n, n Z
Т а к и м о б р а зо м , w i i2 n , г д е n 0 , е с л и у ч е с т ь ,
что w не м ож ет бы ть равны м нулю , ибо пери од ф ункции есть
число, неравное нулю .
63.
6 .9 Н е к о т о р ы е с в о й с т в а т р и г о н о м е т р и ч е с к и х ф у н к ц и й1 . s in z
2 . c o s z
/
c o s z 1 1
/
s i n z 1 2
С праведливость этих ф орм ул устанавливается путем
п очлен н ого диф ф ерен ц и рован ия степ енн ы х р ядов для эти х
ф ункций.
64.
3. С пом ощ ью ф орм ул Э йлера и правил ум н ож ения степенейл егко п р овер и ть, что и звестн ы е тр и го н о м етр и ч ески е ф о р м ул ы
сп равед ли вы и д ля ком п лексн ы х зн ачен и й аргум ен та.
65.
Рассм отрим некоторы е из них:a ) s i n 2 z c o s 2 z l 1 3
Д ействительно,
iz
iz
2
iz
iz
e e e e
s in z c o s z
+
2i
2i
1
iz
iz 2
iz
iz 2
=
e e e e =
4
1 iz
= e e iz e iz e iz e iz e iz e iz
4
1 iz iz
2e 2e e0 l
4
2
2
2
=
e
iz
66.
b) ф орм улы слож ения и вы читанияs in z t s in z c o s t c o s z s in t
1 4
c o s z t c o s z c o s t s i n z s i n t 1 5
Д о к а ж е м , н а п р и м е р , ф о р м у л у 1 4 :
e iz e iz e it e it e iz e iz e it e it
s in z c o s t c o s z s in t
2i
2
2
2i
e
i z t
e
i z t
e
i z t
e
i z t
e
4i
i z t
e
i z t
e
i z t
e
i z t
67.
2e e es in z t
4i
2i
З а м е н я я t н а t, и у ч и т ы в а я , ч т о c o s t - ч е т н а я , s in t - н е ч е т н а я
ф ункции, получим :
2e
i z t
i z t
i z t
i z t
s in z t s in z c o s t c o s z s in t s in z c o s t c o s z s in t
Ф о р м у л а 1 4
д оказан а.
68.
c) Ф орм улы приведения:s in
2
cos
2
s in
2
cos
2
z cos z
z cos z
z cos z
z s in z
Ф о р м у л ы 1 6 - 2 3
1 6 ,
s i n z s i n z
2 0 .
1 7 ,
c o s z c o s z
2 1 .
1 8 ,
s in ( z ) s in z
2 2 .
1 9 ,
c o s z c o s z
2 3 .
в ы т е к а ю т и з ф о р м у л 1 4
и 1 5 .
69.
П окаж ем , наприм ер, справедливость ф орм улы1 6 :
s in z s in c o s z c o s s in z 1 c o s z 0 s in z c o s z
2
2
2
4. С вязь м еж д у ги п ерб оли чески м и и три гон ом етри чески м и
ф ункциям и:
ez e z
ez e z
П о оп ред елен и ю : shz
; chz
.
2
2
Н апом ним свойства этих ф ункций для действительны х
з н а ч е н и й z , т о е с т ь д л я z x , г д е x .
70.
y shx есть н ечетн ая ф ун кц и я, которая является всю д ув о зр а с т а ю щ е й , п р и ч е м п р и х sh x . П р и х 0 гр а ф и к
ф ун кц и и явл яется вы п укл ы м ввер х , а п р и х 0 - вы п укл ы м вн и з:
71.
у chх есть четная ф ункция, которая является убы ваю щ ей прих 0 и возрастаю щ ей п ри х 0. Г раф и к ф ун кц и и является
вы пуклы м вниз
72.
И м еемs in iz
e
i iz
e
2i
i iz
e
c o s iz
2i
Т аки м об разом ,
e
i iz
i iz
e z ez
ez e z
i
is h z
2i
2
e z ez
chz
2
s in iz is h z ; c o s iz c h z
2 4
73.
5 . Н у л я м и ф у н к ц и и w s i n z я в л я ю т с я ч и с л а n , г д е n .П у с т ь s i n z 0 , г д е n . Т о г д а
s in х iy s in х c o s iy c o s x s in iy s in x c h y i c o s х s h y 0
З д е с ь м ы в о с п о л ь з у е м с я ф о р м у л а м и 1 4
и
2 4 .
К ом плексное число равно нулю , если равны нулю
s in x c h y 0 ,
действительная и м ним ая части, то есть, если:
cos xshy 0.
74.
Т а к к а к c h y 0 п р и л ю б о м y , т о д о л ж н о б ы т ь s i n x 0 .О т к у д а с л е д у е т , ч т о х n , г д е n .
П о д ставл яя н ай д ен н о е зн ач ен и е х во вто р о е ур авн ен и е:
cos nshy 0.
n
И м е е м , 1 sh y 0 . С л е д о в а т е л ь н о , sh y 0 , т о е с т ь у 0 .
Т а к и м о б р а з о м , z x i y n , г д е n .
А н алоги чн о п оказы ваем , что н улям и ф ун кц и и w cos z
я в л я ю т с я ч и с л а z k , k .
2
75.
6 . Ф у н к ц и и w s in z и w c o s z я в л я ю т с я п е р и о д и ч е с к и м и , и хпериодам и являю тся числа, кратны е 2 .
В с а м о м д е л е , п у с т ь w е с т ь п е р и о д ф у н к ц и и s in z . П о
о п р ед ел ен и ю п ер и о д а ф ун кц и и это о зн ач ает, ч то
s i n z w s i n z д л я л ю б о г о z .
О т к у д а , s in z w s in z 0 .
w
w
П р е о б р а з у е м в п р о и з в е д е н и е , п о л у ч и м : 2 c o s z s in 0 .
2
2
76.
Т ак как равен ство долж н о б ы ть сп равед ли вы м д ля лю б ого z,w
т о э т о б у д е т т о г д а , к о г д а s in 0 .
2
w
П оэтом у
n , т о е с т ь w 2 n , гд е n { 0} .
2
Здесь м ы n 0 исклю чаем , ибо период ф ункции есть числo,
неравное нулю .
П од об н ы м ж е об разом устан авли вается сп равед ли вость
утвер ж д ен и я и д л я ф ун к ц и и co s z.
77.
7. Д ля ком п лексн ы х зн ачен и й аргум ен та уж е н ельзя утверж д ать,ч т о | s i n z | 1 и
c o s z 1, и б о и з с о о т н о ш е н и я s in iy is h y и
c o s iy ic h y с л е д у е т , ч т о s in iy s h y и c o s iy c h y , a s h y и
c h y , г д е y , н е о г р а н и ч е н ы .
78.
6 .1 0 О т о б р а ж е н и е п о с р е д с т в о м п о к а з а т е л ь н о йф ункции
Р а с с м о т р и м ф у н к ц и ю w e z ,к о т о р а я о п р е д е л е н а и я в л я е т с я
аналитической на всей z плоскости.
П окаж ем , что лю бая точка w 0 0 им еет хотя бы один прообраз
в z плоскости.
79.
Д л я э т о г о р е ш и м у р а в н е н и е w 0 e z о т н о с и т е л ь н о z x iyw0 e
x iy
Т огда w
w 0 e xe
0
x iy
w0 e
e x и A rgw 0= y. И з w
З н а ч и т z ln w
0
п р и k 0 , z 0 = ln w
A r g w 0 ln w
0
0
c o s
x
0
y i s in y
e x н а х о д и м x ln w 0 .
i ( a r g w 0 2 k ) , k 0 , 1 , 2 , . . .
i a rg w 0.
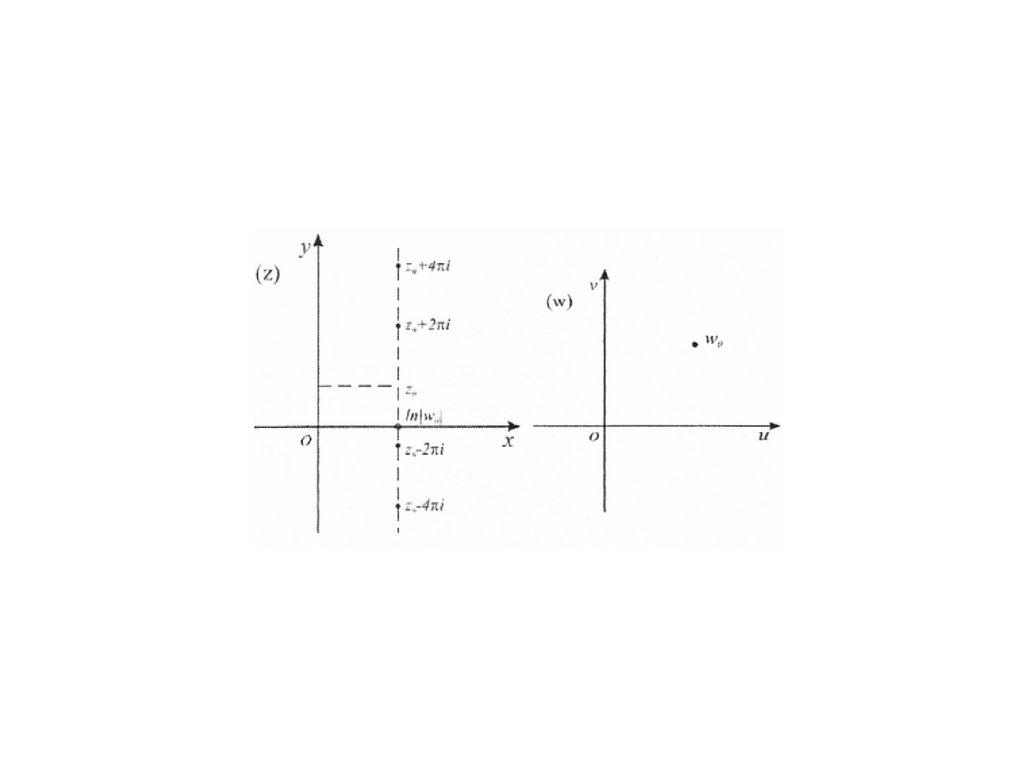
Т аки м об разом , лю б ая точка w 0 и м еет б ескон ечн о м н ого
п рооб разов, которы е расп олож ен ы н а п рям о й , п араллельн ой
оси О у, и н аходятся друг от друга н а расстояни и , кратн ом 2 .
80.
81.
И з преды дущ их рассуж дений видно, что z - плоскостьп о ср ед ство м п о казател ьн о й ф ун кц и и о то б р аж ается н а о б ласть,
получаю щ ую ся из w - плоскости ислю чением одной точки
w 0 . П ри ч ем о то б р аж ен и е это н е взаи м н о о д н о зн ач н о .
82.
Н а z - плоскости рассм отрим областьD
2
= z | z x iy x 0 y 2 . Н а й д е м е е о б р а з
п р и о то б р аж ен и и w e z.
w e x е iу , w e x . Е с л и x , т о 0 w .
A rgw y, зн ачи т, 0 A rgw 2 .
Т аки м об разом лю б ая точка z D
2
отображ ается в область Q
получаю щ ую ся из w - плоскости удалением действительной
неотрицательной полуоси.
83.
В ерн о и об ратн ое: п рооб разом лю б ой точки w Q , являетсяе д и н с т в е н н а я т о ч к а z D 2 .
84.
И так, м ы и м еем взаи м н о од н озн ачн ое отоб р аж ен и е об ластиD 2 н а о б л а с т ь Q п о с р е д с т в о м п о к а з а т е л ь н о й ф у н к ц и и .
О бласть D
2
н азы в ается о б л астью о д н о л и стн о с ти ф ун к ц и и w e z.
О чеви д н о, что об ластью од н оли стн ости п оказательн ой ф ун кц и и
будет внутренность лю бой полосы , параллельрной
действительной оси, ш ирина которой м еньш е или равна 2 .





















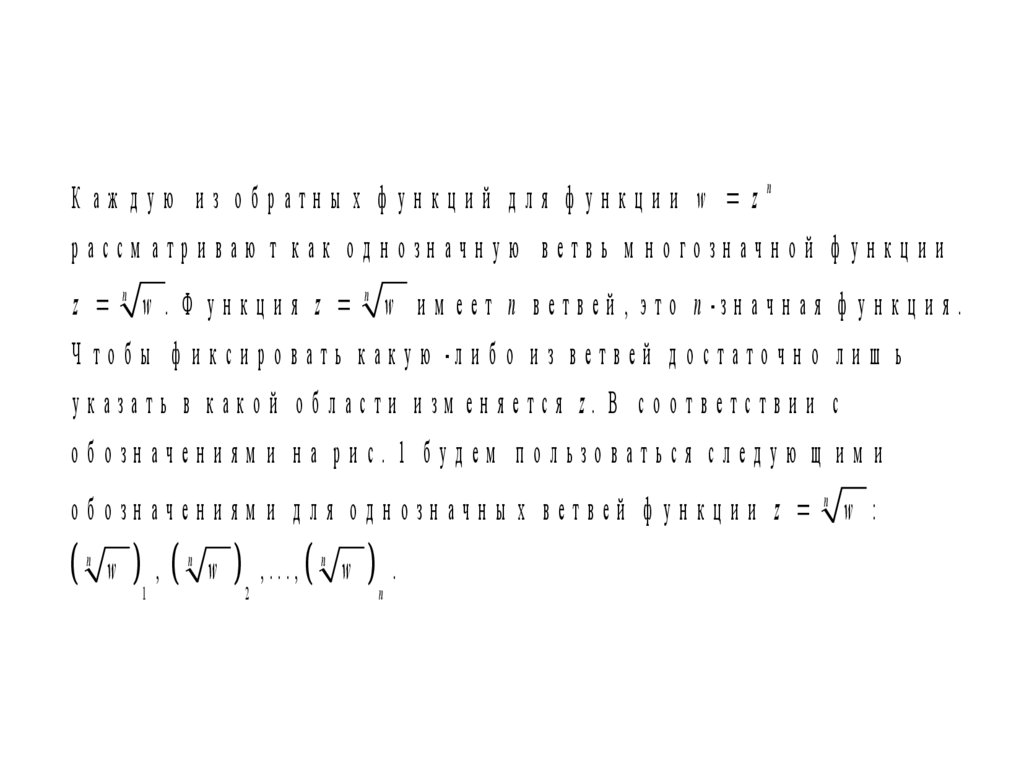

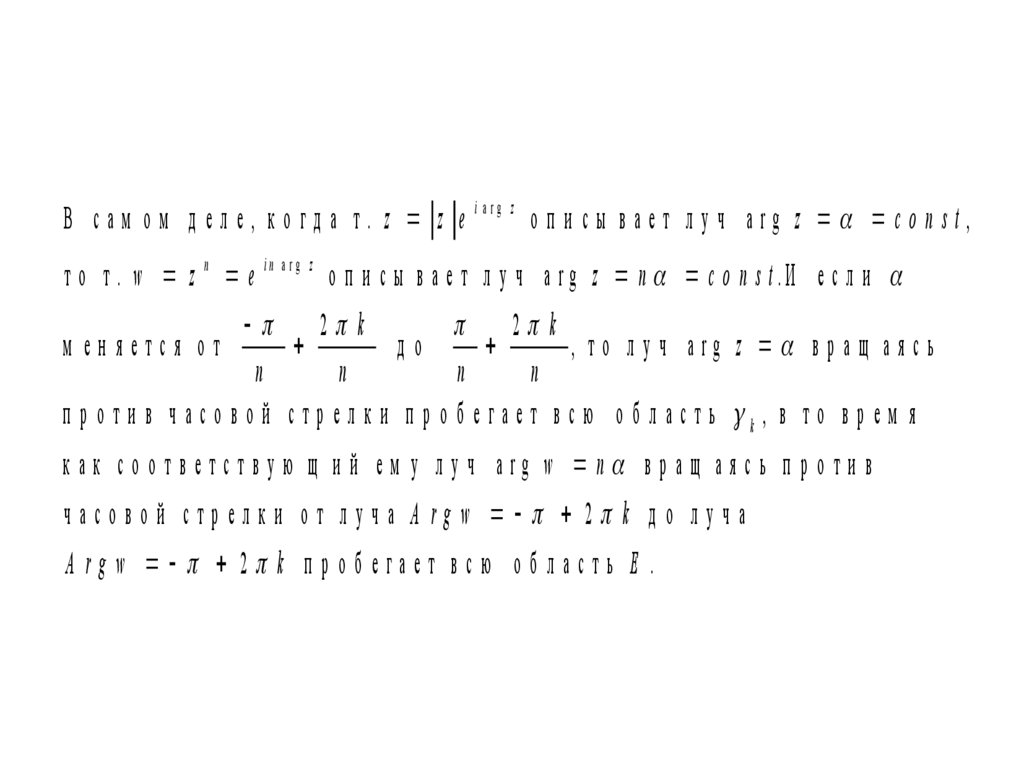








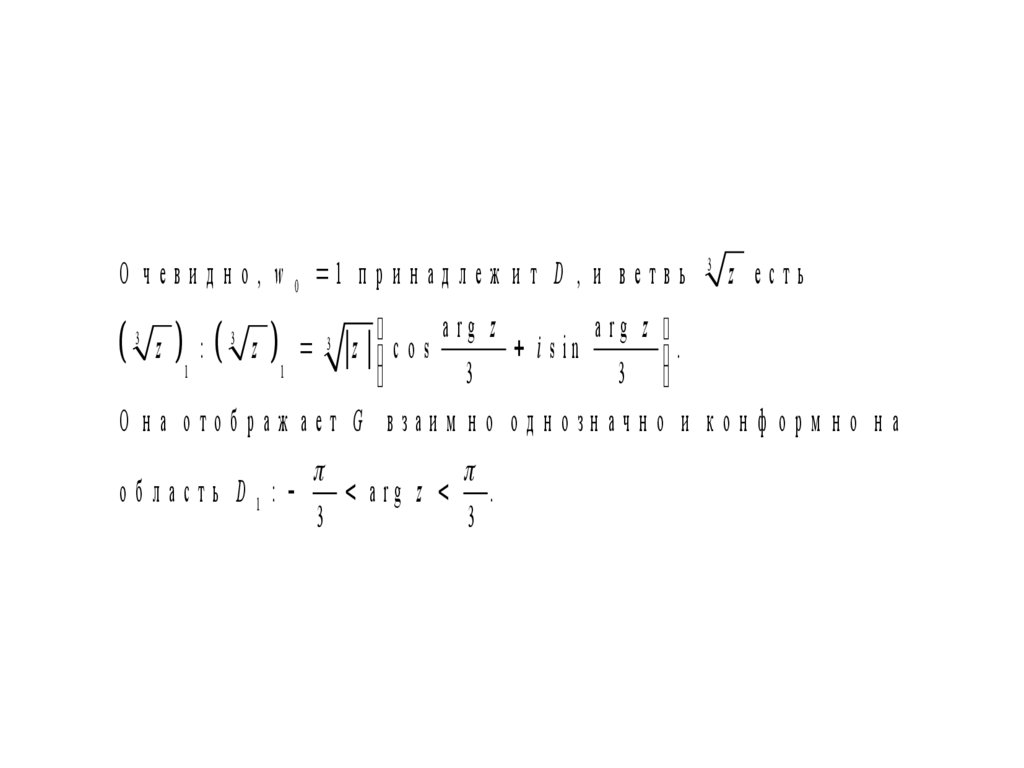












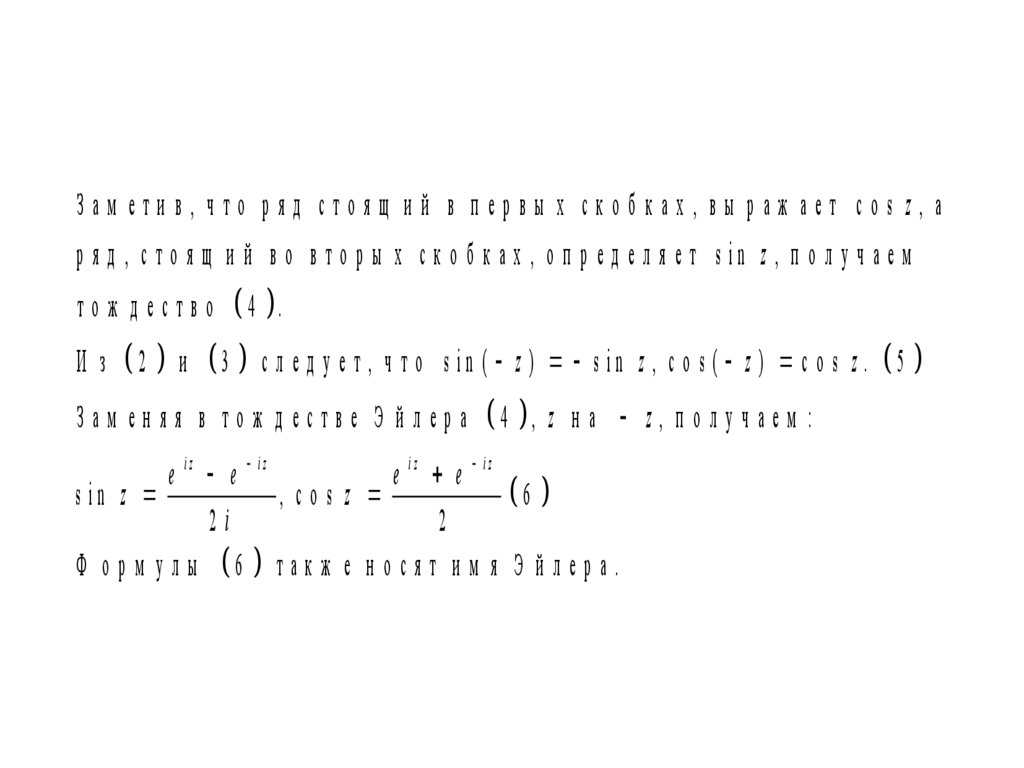































 informatics
informatics








