Работа с текстовой задачей для развития математической грамотности обучающихся 4-5 классов

1. Работа с текстовой задачей для развития математической грамотности обучающихся 4-5 классов

Юнчик Анна Ивановна,
учитель начальных классов

2. Цель обучения математике

Обучение математике в начальной школе
призвано сформировать у детей начальную
математическую грамотность: знание базового
курса арифметики, необходимые вычислительные
навыки, умение проводить простейшие
рассуждения в ходе решения текстовых задач,
первичные навыки математической речи и
письма.
Тем самым начальная школа должна
обеспечить подготовку детей к успешному
изучению систематических курсов математики.

3. Работа с условием задачи

Можно использовать следующие формы работы с
условием задачи, такие как:
▪ Составление вопроса или вопросов к условию
задачи.
▪ Составление текста задачи по рисунку.
▪ Восстановление задачи из так называемого
«деформированного» текста.

4. Осмысление текста – наиболее трудный этап в работе с текстовой задачей

Часть условия
выражена в
повествовательной
форме, затем идёт
вопросительное
предложение,
содержащее вопрос и
часть условия
Текст задачи
представляет одно
сложное
вопросительное
предложение, в
котором сначала стоит
вопрос задачи, а затем
условие задачи
Текст задачи – одно
большое
повествовательное
предложение, в
котором сначала
стоит вопрос задачи,
а затем её условие.
Формулировка У Оли было 6 яблок.
Сколько яблок стало у
Оли, если она два
отдала брату?
Сколько яблок осталось
у Оли после того, как
она отдала два яблока
брату, а было у неё 6
яблок?
Найди количество
яблок у Оли после
того, как она из
своих 6 яблок отдала
2 яблока отдала
брату.
Конструкция

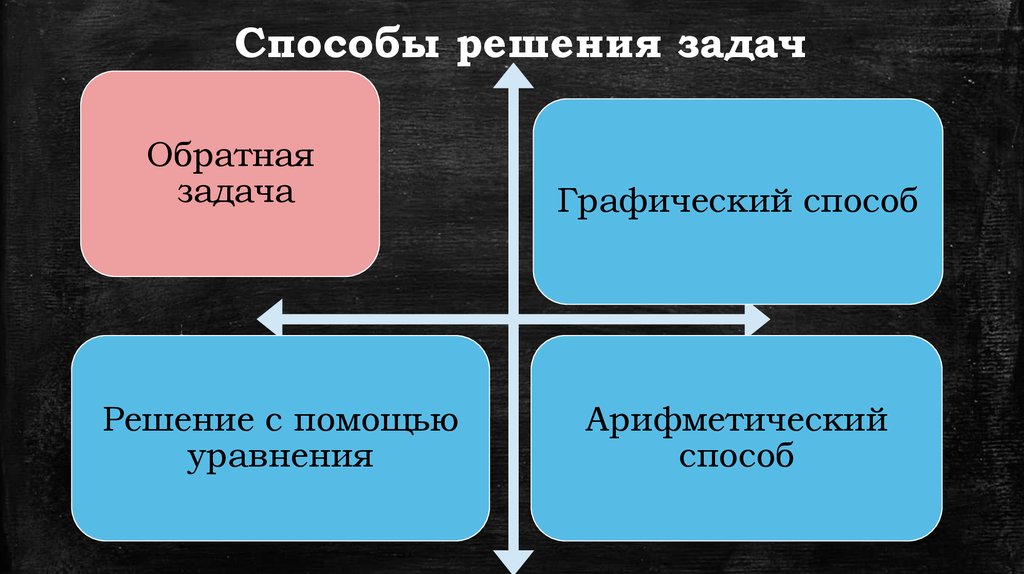
5. Способы решения задач

Обратная
задача
Решение с помощью
уравнения
Графический способ
Арифметический
способ

6. Обратные задачи

Составление и решение обратных
задач – один из интереснейших
способов проверки задачи.
При этом дети наиболее полно
понимают связи между величинами и
наблюдают обратные по отношению
друг к другу действия.
Обратной задачей к данной
является та, которая содержит искомое
число в качестве известного, а какоелибо из известных чисел прямой задачи
становится неизвестным.

7.

Эти задачи являются обратными
Из двух сёл, расстояние между
которыми 69 км навстречу
друг другу выехали два
велосипедиста. Через какое
время они встретятся, если
скорость одного 11 км/ч, а
другого – 12км/ч.
Из двух сёл навстречу друг
другу выехали одновременно
два велосипедиста и
встретились через 3 часа.
Каково расстояние между
селами, если их скорости 11
км/ч и 12 км/ч соответственно.

8. Для выполнения проверки решения прямой задачи способом составления обратной задачи и ее решения, дети должны овладеть следующим

алгоритмом:
1. Решить исходную задачу.
2. Подставить результат
известного данного.
в
текст
исходной
задачи
в
качестве
3. Обозначить новое неизвестное в задаче.
4. Составить новую задачу по отношению к данной.
5. Решить составленную задачу.
6. Сравнить полученный результат с тем данным, которое сделали
неизвестным.
7. Сделать соответствующий вывод (если числовые значения совпадут,
то задача решена верно).

9.

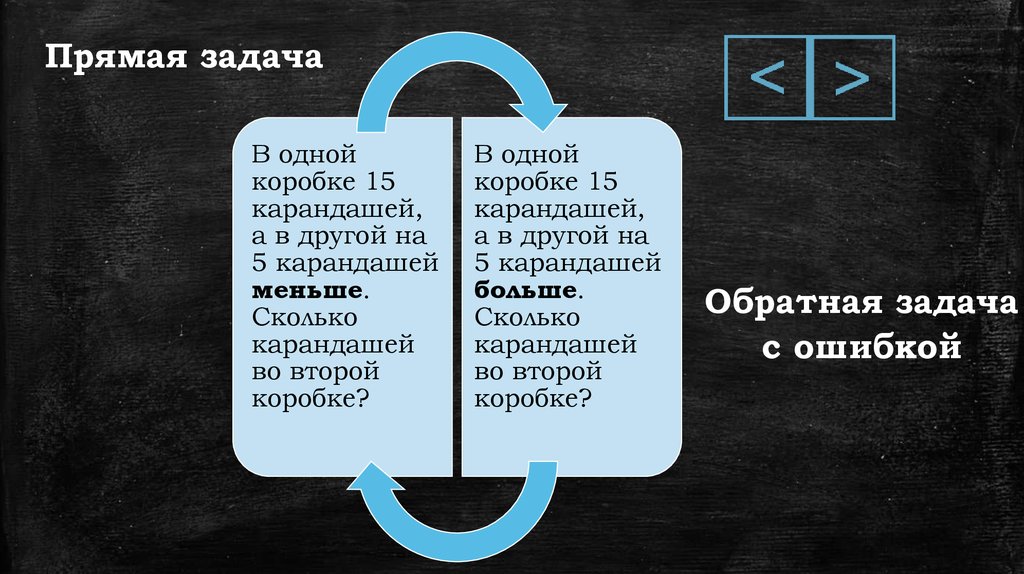
Прямая задача
В одной
коробке 15
карандашей,
а в другой на
5 карандашей
меньше.
Сколько
карандашей
во второй
коробке?
В одной
коробке 15
карандашей,
а в другой на
5 карандашей
больше.
Сколько
карандашей
во второй
коробке?
Обратная задача
с ошибкой

10.

Прямая задача
I – 15 кар.
II – ?, на 5 кар.
меньше
Обратные задачи
I – 15 кар.
II – 10 кар., на ?
меньше
I – ? кар.
II – 10 кар., на 5
меньше
Схематическое
изображение
задачи
позволяет
учащимся
пронаблюдать, что при составлении обратной задачи изменяются только
числовые значения, отношения в задаче остаются неизменными.

11. При организации деятельности учащихся над задачей после ее решения можно использовать следующие виды работы:

элементарное исследование решения задачи (при каких условиях задача
имеет одно или несколько решений и не имеет решения; как будет изменяться
ответ задачи, если изменять данные и т.д.);
сравнить решения обратных задач, пронаблюдать зависимости и т.д.;
изменить требование задачи так, чтобы задача решалась иначе;
составить другую задачу по вопросу данной;
составить аналогичную задачу, но с другими числами и другим сюжетом;
изменить требование задачи, но решение задачи осталось бы неизменным;
составить все возможные требования, которые можно поставить к данному
условию и т.д.

12.

СПАСИБО
ЗА ВНИМАНИЕ!