Канальное кодирование. Основы помехоустойчивого кодирования

1. Основы помехоустойчивого кодирования

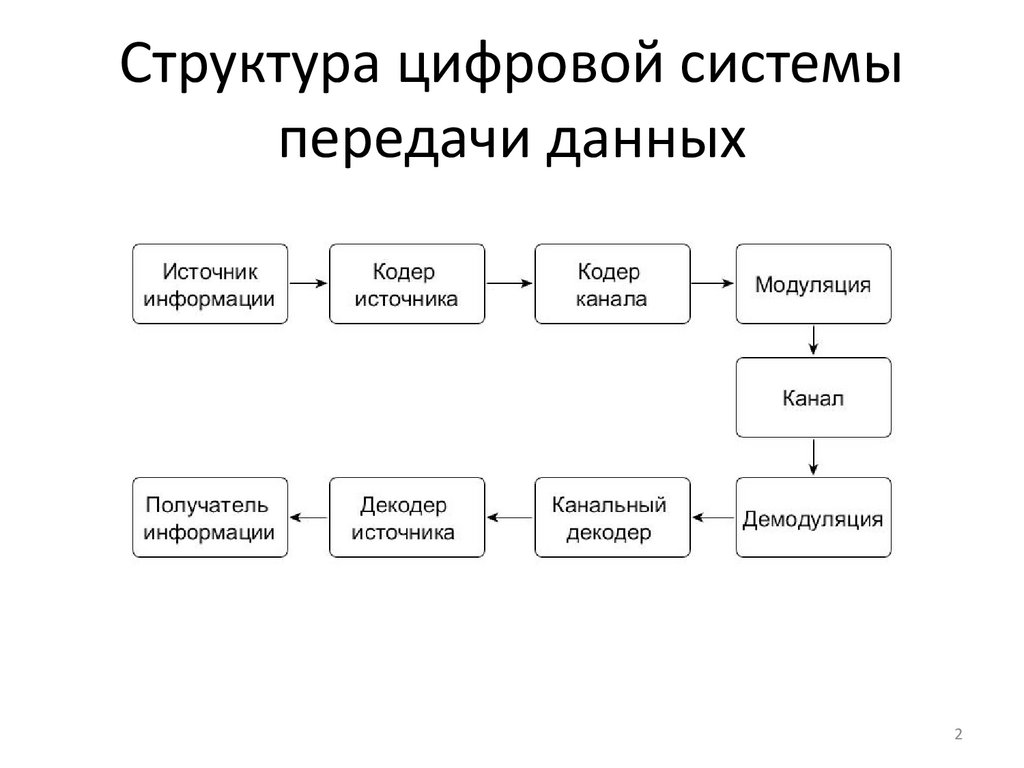
2. Структура цифровой системы передачи данных

2

3. Предел Шеннона (теорема Шеннона — Хартли)

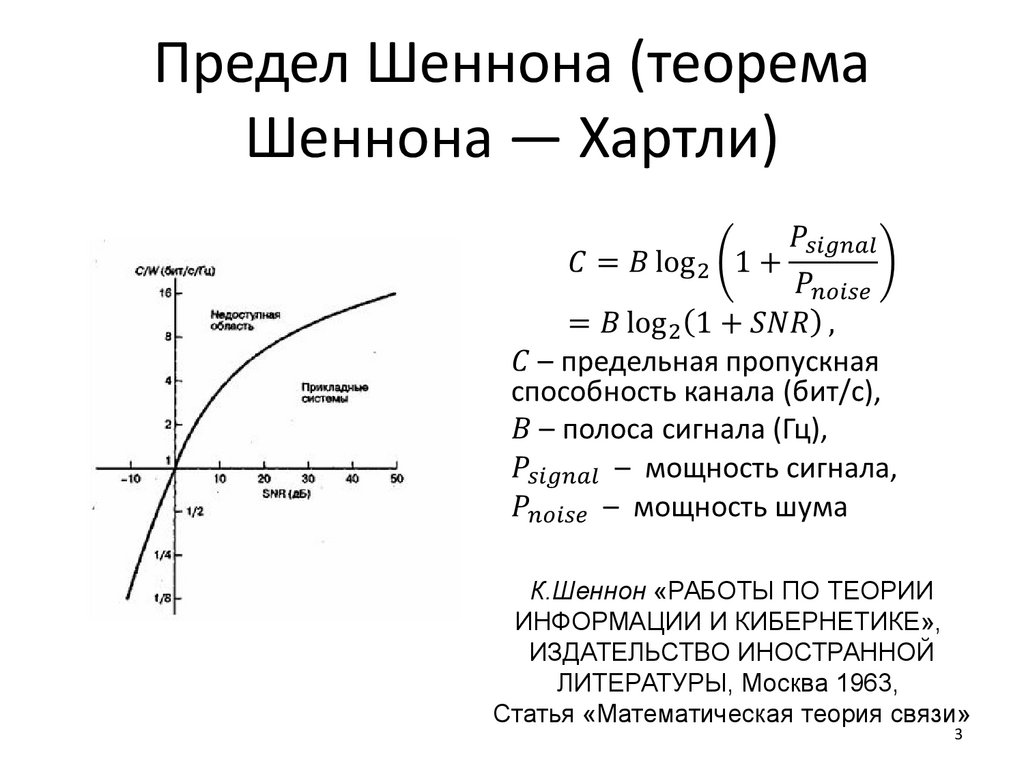
Предел Шеннона (теорема
Шеннона — Хартли)
К.Шеннон «РАБОТЫ ПО ТЕОРИИ
ИНФОРМАЦИИ И КИБЕРНЕТИКЕ»,
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ
ЛИТЕРАТУРЫ, Москва 1963,
Статья «Математическая теория связи»
3

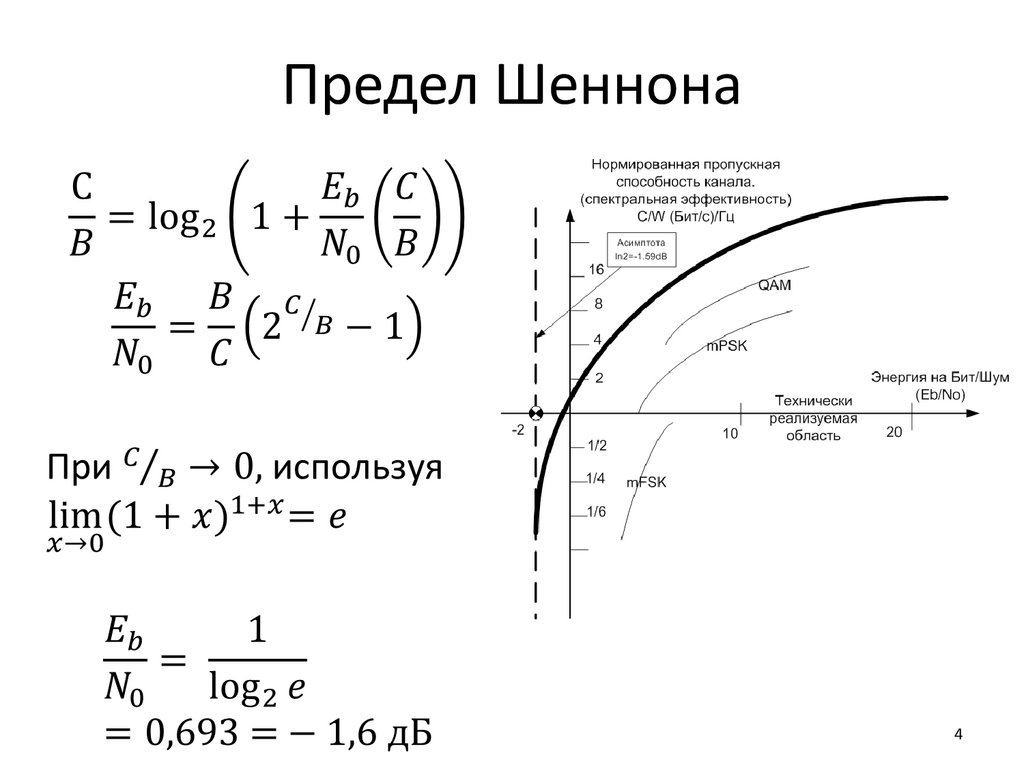
4. Предел Шеннона

4

5. Классификация кодов, исправляющих ошибки (ЕСС)

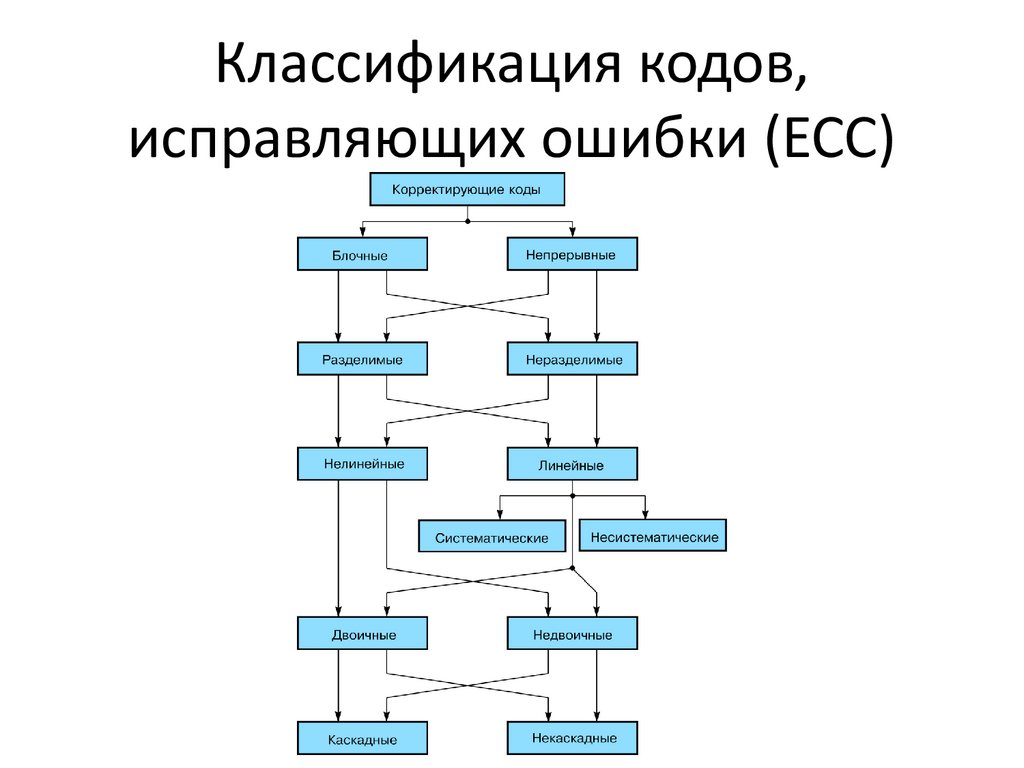
6. Классификация кодов, исправляющих ошибки (ЕСС)

Наиболее многочисленный класс разделимых кодов составляют линейные
коды. Основная их особенность состоит в том, что избыточные символы
образуются как линейные комбинации информационных символов.
В свою очередь, линейные коды могут быть разделены на два подкласса:
систематические и несистематические. Все двоичные систематические
коды являются групповыми. Это означает, что все кодовые комбинации,
относящиеся к группе, обладают тем свойством, что сумма по модулю два
любой пары кодов снова дает кодовую комбинацию, принадлежащую этой
группе. Линейные коды, которые не могут быть отнесены к подклассу
систематических, называются несистематическими. Нелинейные коды
свойствами групповых кодов не обладают.
Наиболее известными представителями систематических кодов являются
циклические коды и коды Хемминга.

7. Расстояние Хэмминга

Расстояние Хэмминга:
g – количество ошибок,
которые можно исправить
7

8. Код Хемминга

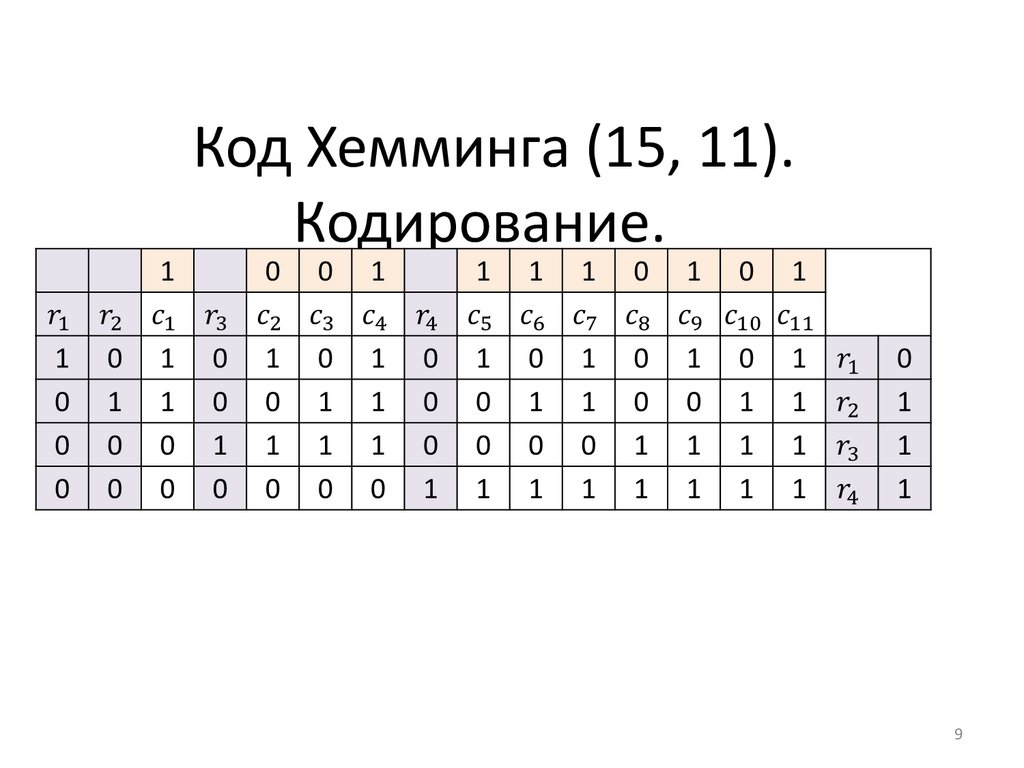
8

9. Код Хемминга (15, 11). Кодирование.

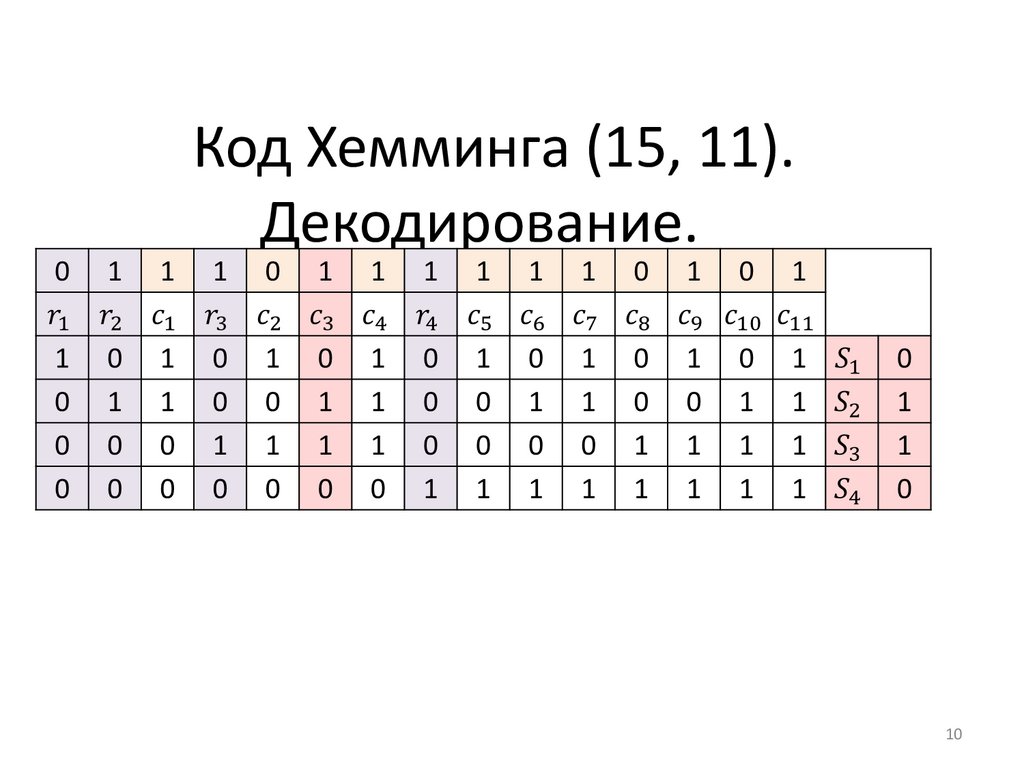
9

10. Код Хемминга (15, 11). Декодирование.

10

11. Идея кодирования. Проверка четности.

11

12. Идея кодирования. Код повторения.

12

13. Система передачи информации

Корректирующие коды,
используемые в системах ЦТВ
• Блоковые
– Рида-Соломона
– БЧХ
– LDPC
• Сверточные
(кодовое ограничение К – количество учитываемых
при кодировании предшествующих символов)
• Каскадные
• Турбокоды

14. Общие сведения

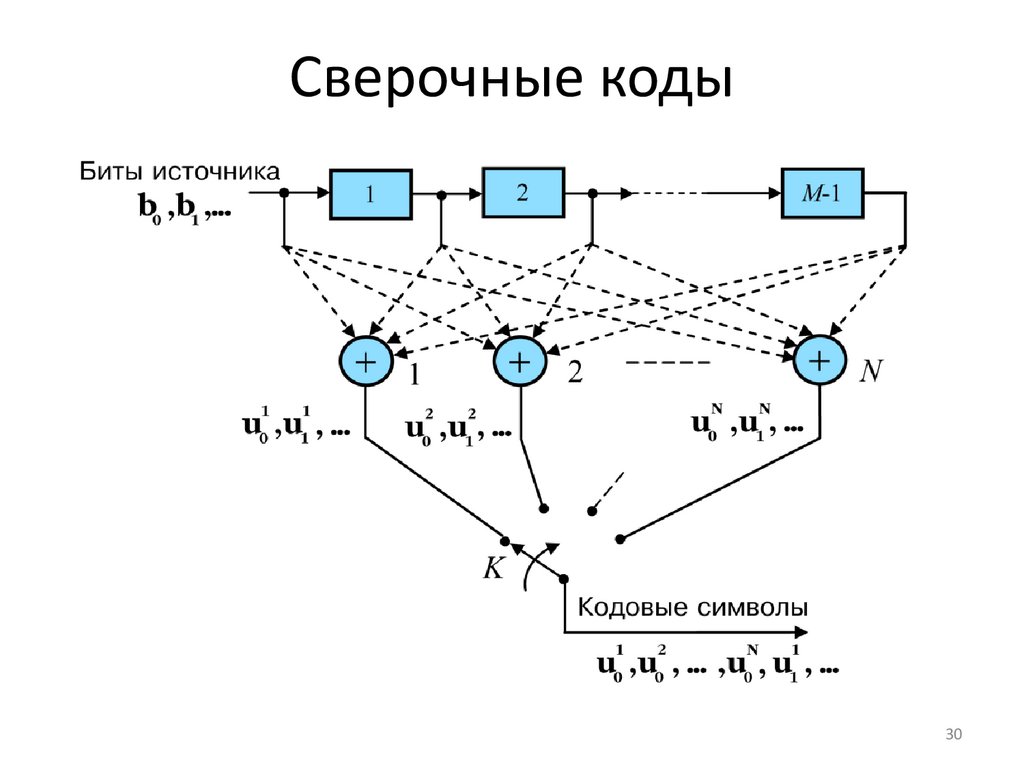
Сверочные коды
30

15. Цифровая система связи

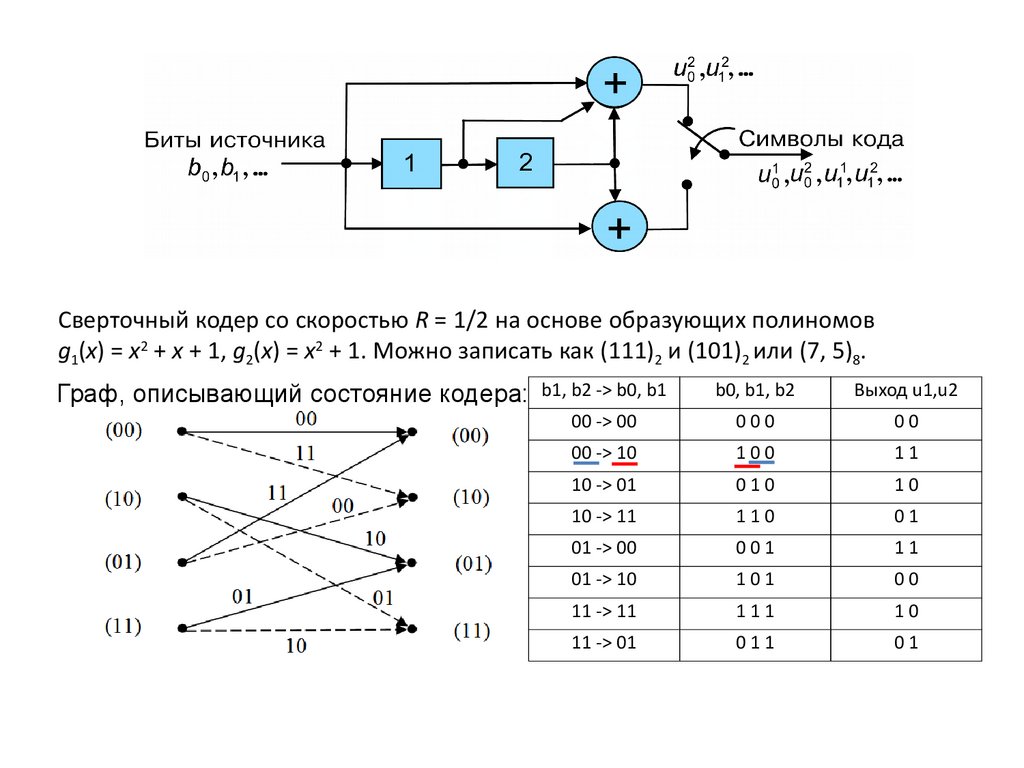
Сверточный кодер со скоростью R = 1/2 на основе образующих полиномов
g1(x) = x2 + x + 1, g2(x) = x2 + 1. Можно записать как (111)2 и (101)2 или (7, 5)8.
Граф, описывающий состояние кодера:
b1, b2 -> b0, b1
b0, b1, b2
Выход u1,u2
00 -> 00
000
00
00 -> 10
100
11
10 -> 01
010
10
10 -> 11
110
01
01 -> 00
001
11
01 -> 10
101
00
11 -> 11
111
10
11 -> 01
011
01

16. Общие сведения

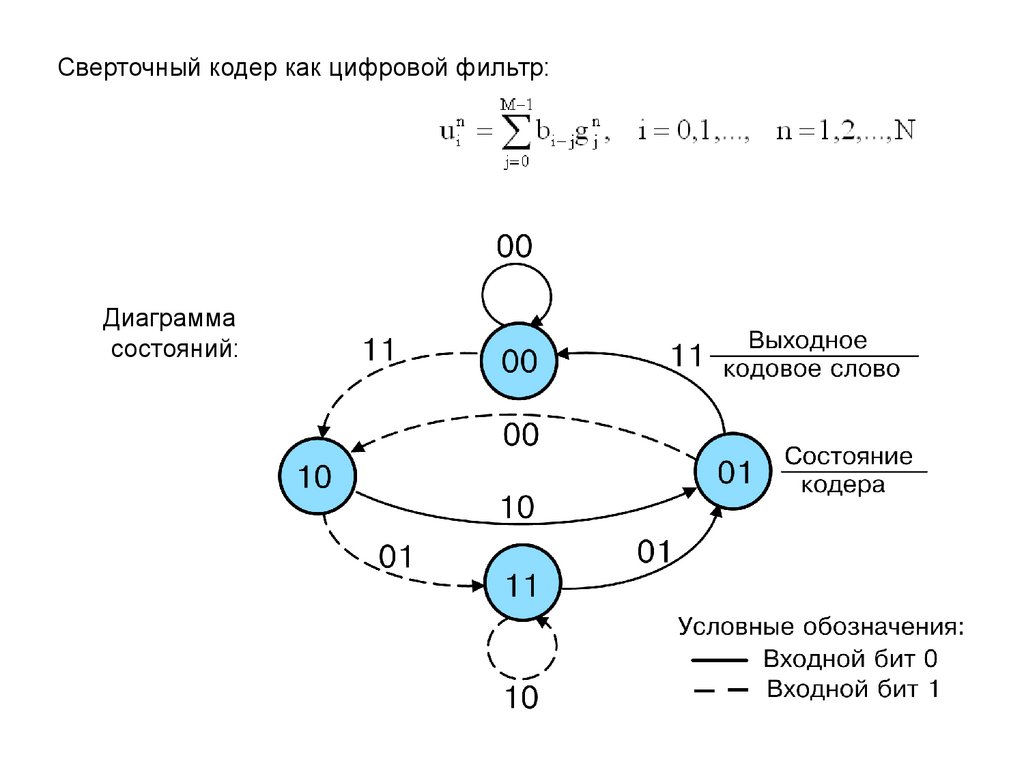
Сверточный кодер как цифровой фильтр:
Диаграмма
состояний:

17. О помехоустойчивом кодировании

Граф,
описывающи
й
состояние
кодера:
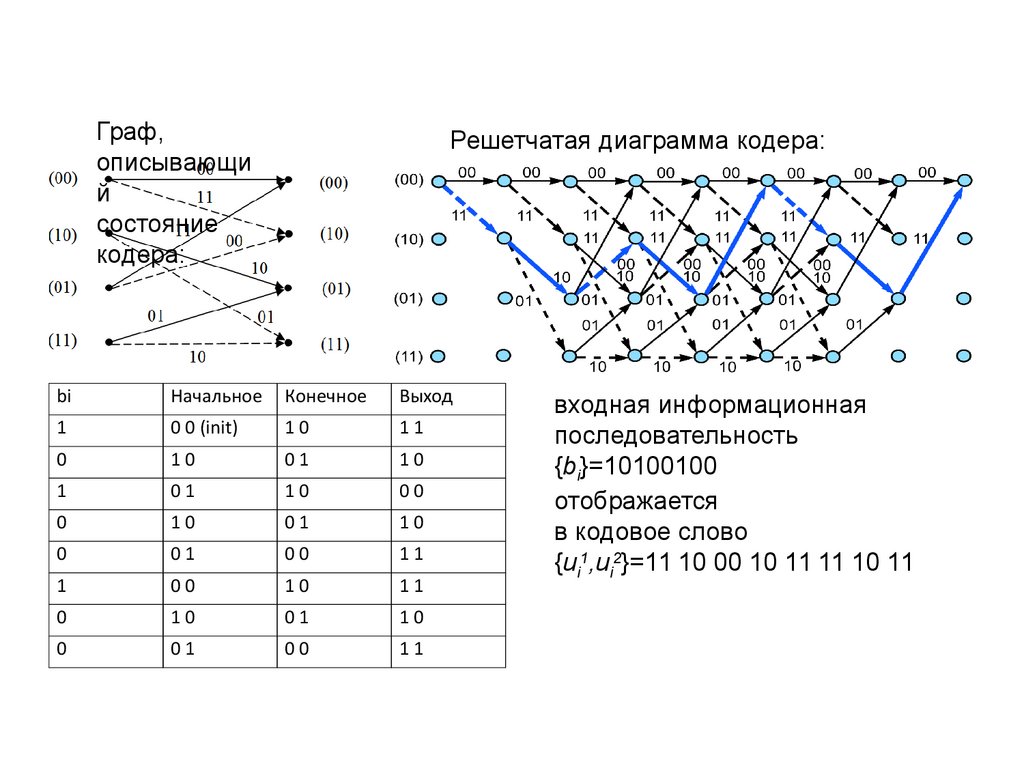
Решетчатая диаграмма кодера:
bi
Начальное
Конечное
Выход
1
0 0 (init)
10
11
0
10
01
10
1
01
10
00
0
10
01
10
0
01
00
11
1
00
10
11
0
10
01
10
0
01
00
11
входная информационная
последовательность
{bi}=10100100
отображается
в кодовое слово
{ui1,ui2}=11 10 00 10 11 11 10 11

18. О помехоустойчивом кодировании

Декодирование сверточных кодов
Алгоритм Витерби
На i–м шаге декодирования, в течение которого принимается i–я n–символьная кодовая группа
наблюдения выполняются следующие операции:
1.Определяются хэмминговы расстояния между принятой n–символьной кодовой группой и
каждой из ветвей решетчатой диаграммы. Поскольку из каждого из 2 M-1 узлов выходят две
ветви, всего вычисляется 2M расстояний.
2.Рассматриваются две ветви, идущие из разных предшествующих состояний к каждому из 2 M-1
узлов:
• Отвечающие указанным ветвям расстояния Хэмминга прибавляются к накопленным до
i–го шага расстояниям Хэмминга двух соответствующих путей для получения новых
значений расстояний. Указанное накапливаемое расстояние пути называется
метрикой.
• Сравниваются метрики двух соревнующихся путей, идущих в одно и то же состояние.
Путь, находящийся на большем расстоянии от наблюдения, чем другой, отбрасывается
и больше не учитывается в процедуре декодирования. Оставшийся путь называется
выжившим путем.
3.Для всех 2M-1 выживших путей запоминаются значения их метрик и декодер готов к переходу
на (i+1)–й шаг процедуры.

19. О помехоустойчивом кодировании

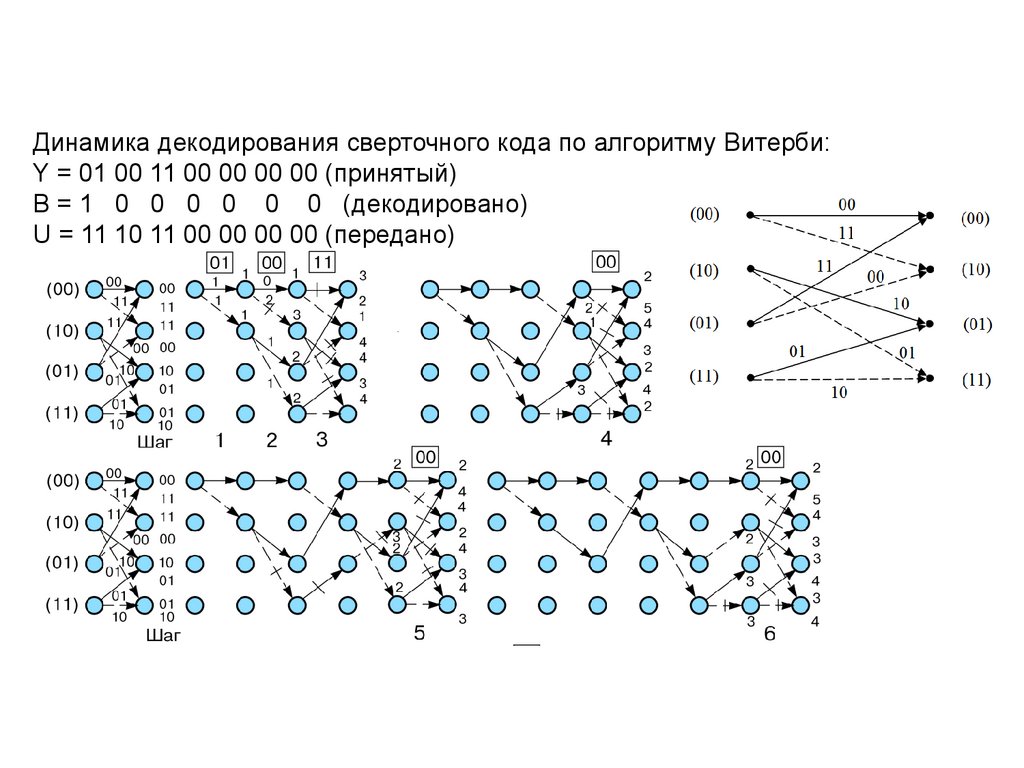
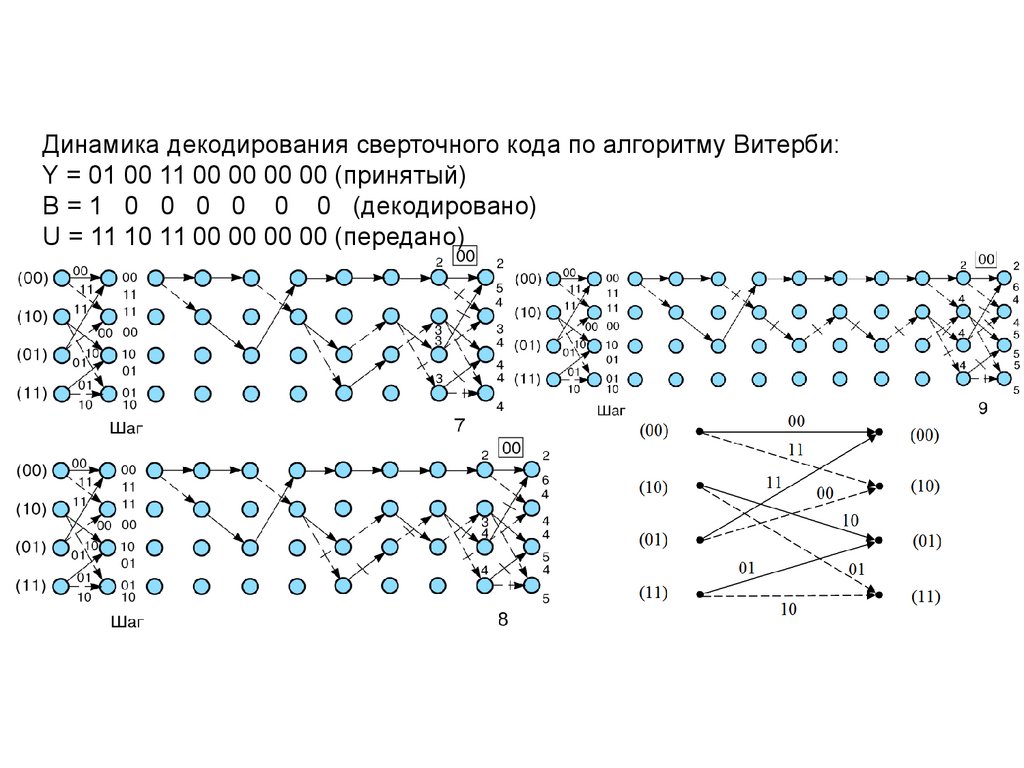
Динамика декодирования сверточного кода по алгоритму Витерби:
Y = 01 00 11 00 00 00 00 (принятый)
B = 1 0 0 0 0 0 0 (декодировано)
U = 11 10 11 00 00 00 00 (передано)

20. Блоковое кодирование

Динамика декодирования сверточного кода по алгоритму Витерби:
Y = 01 00 11 00 00 00 00 (принятый)
B = 1 0 0 0 0 0 0 (декодировано)
U = 11 10 11 00 00 00 00 (передано)

21. Блоковое кодирование

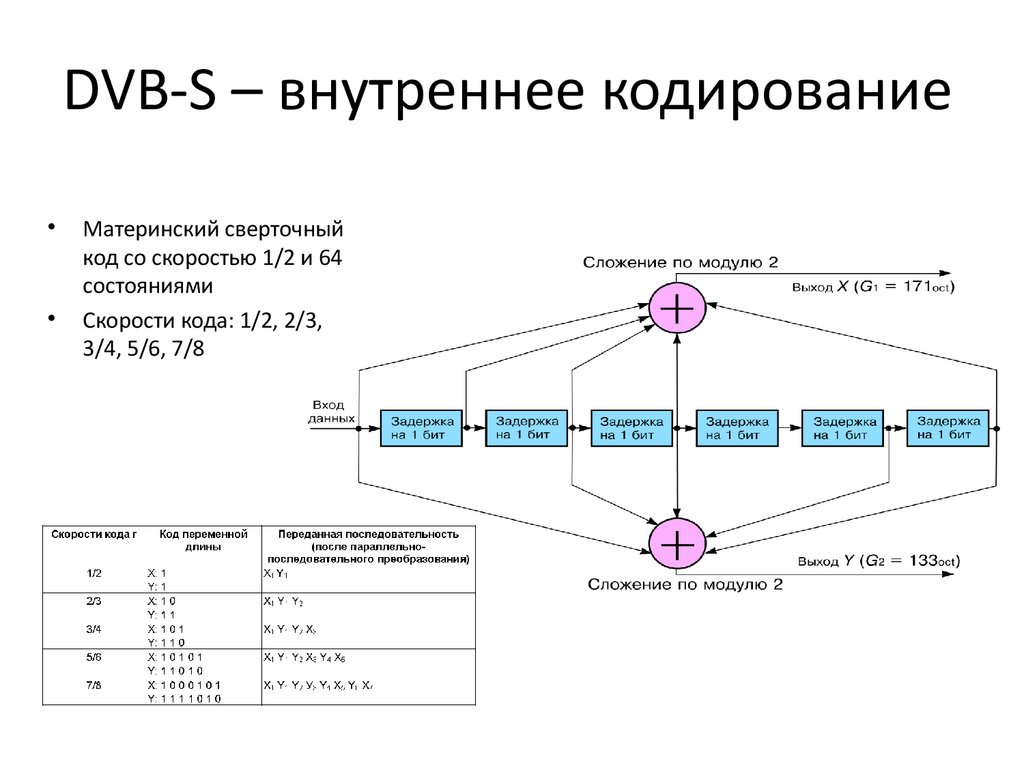
DVB-S – внутреннее кодирование
Материнский сверточный
код со скоростью 1/2 и 64
состояниями
Скорости кода: 1/2, 2/3,
3/4, 5/6, 7/8

22. Блоковое кодирование

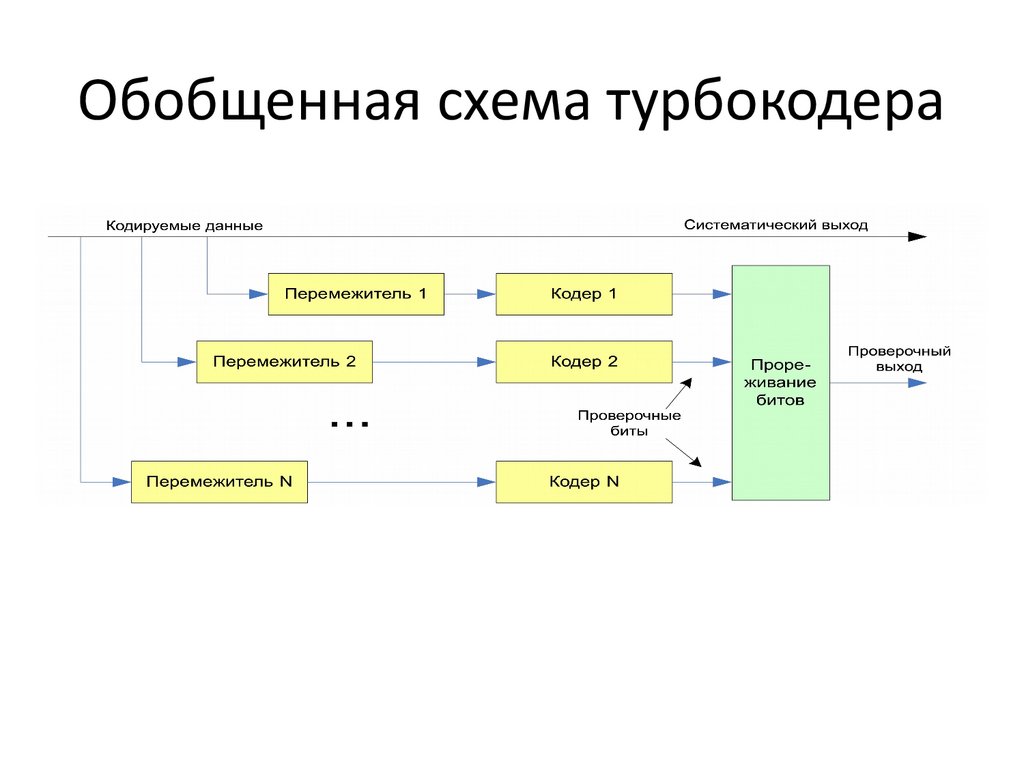
Обобщенная схема турбокодера

23. Блоковое кодирование

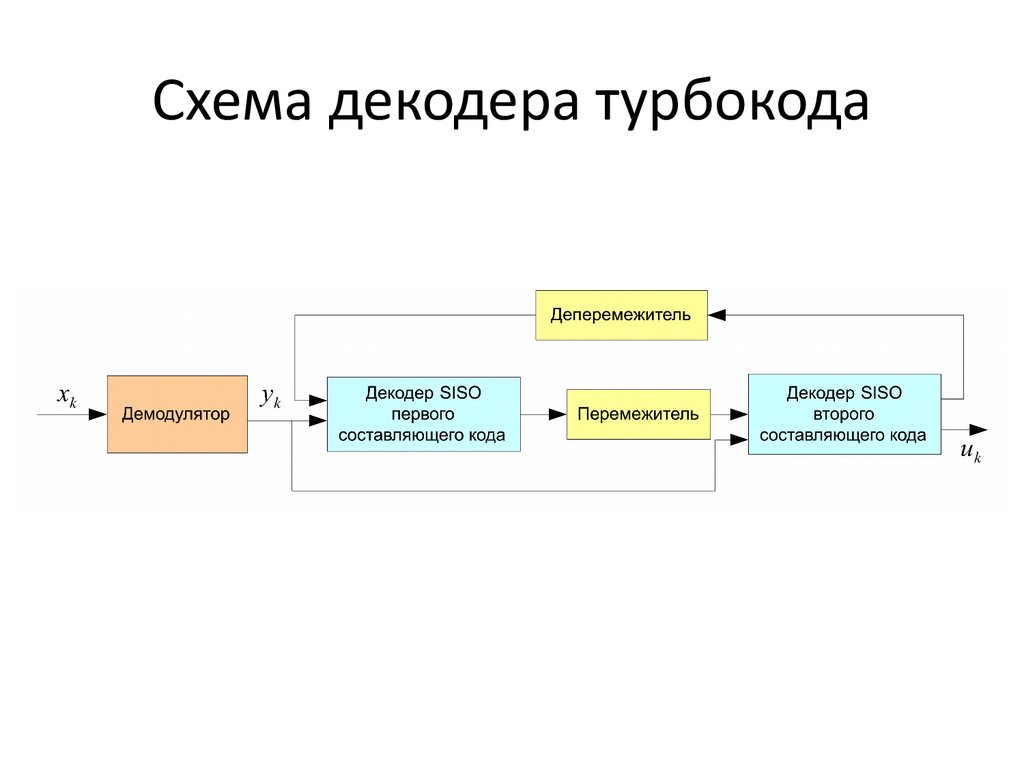
Схема декодера турбокода

24. Неблоковое кодирование

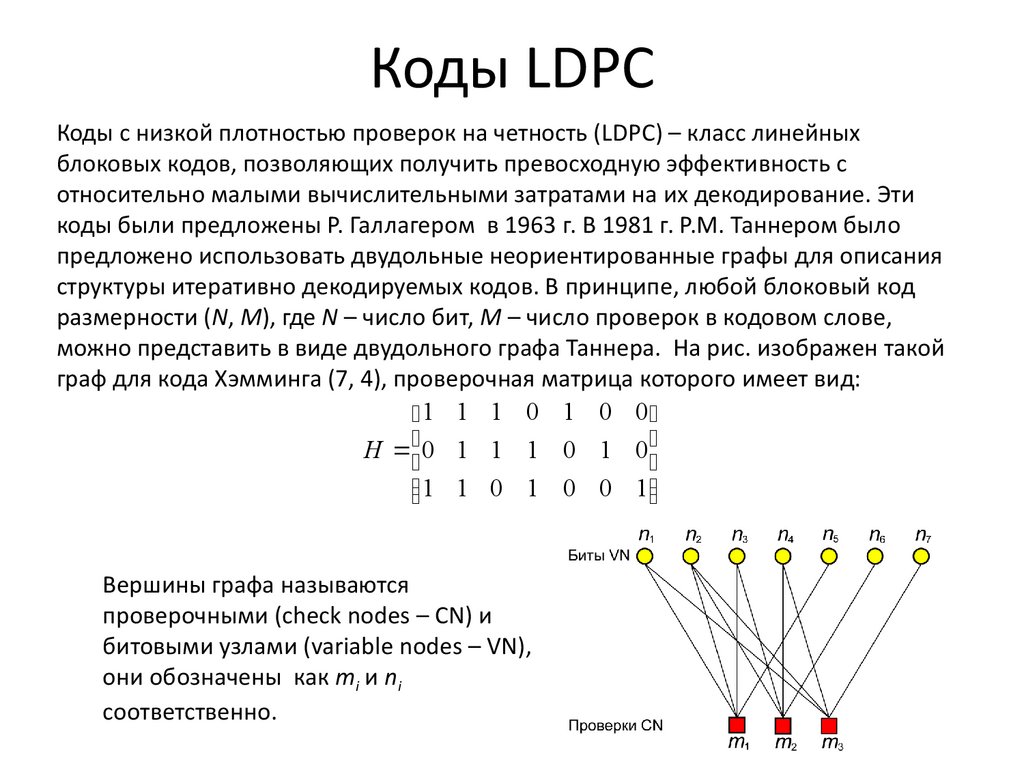
Коды LDPC
Коды с низкой плотностью проверок на четность (LDPC) – класс линейных
блоковых кодов, позволяющих получить превосходную эффективность с
относительно малыми вычислительными затратами на их декодирование. Эти
коды были предложены Р. Галлагером в 1963 г. В 1981 г. Р.М. Таннером было
предложено использовать двудольные неориентированные графы для описания
структуры итеративно декодируемых кодов. В принципе, любой блоковый код
размерности (N, M), где N – число бит, M – число проверок в кодовом слове,
можно представить в виде двудольного графа Таннера. На рис. изображен такой
граф для кода Хэмминга (7, 4), проверочная матрица которого имеет вид:
1 1 1 0 1 0 0
H 0 1 1 1 0 1 0
1 1 0 1 0 0 1
Вершины графа называются
проверочными (check nodes – CN) и
битовыми узлами (variable nodes – VN),
они обозначены как mi и ni
соответственно.

25. Неблоковое кодирование

Коды LDPC
При помощи графа Таннера большинство алгоритмов декодирования LDPC кодов
можно представить в виде процесса последовательного обмена сообщения между
соединенными ребрами вершинами. Для проверочных и битовых узлов графа
вводиться понятия степени – величины, показывающей число ребер входящих в
рассматриваемый узел. Степени битовых и проверочных узлов обозначаются dc и
dr соответственно. Если dc и dr фиксированы для всех узлов, код называют
регулярным, а если хотя бы один из этих параметров изменяется от узла к узлу –
нерегулярным. Для описания нерегулярных кодов вводится ряд распределения
степеней, показывающий долю узлов, имеющих конкретную степень.
В 1996 г. вышла в свет первая после Р. Галлагера работа, посвященная
использованию LDPC кодов в качестве кодов, способных вплотную приблизиться к
границе Шеннона при достаточно большой длине кодового слова. Появление этой
статьи породило целую волну исследований, посвященных поиску новых, более
эффективных структур LDPC кодов, а также альтернативных алгоритмов их
декодирования с различными соотношениями
эффективность/производительность.
Использование LDPC кодов предусматривает большинство современных
стандартов передачи данных (например, IEEE 802.11, IEEE 802.16) и цифрового
вещания (например, DVB‑S2, DVB‑T2, DVB‑C2).

26. Неблоковое кодирование

Классификация кодов LDPC
По определению, данному Р. Галлагером, код LDPC – это линейный код,
проверочная матрица H которого, размерности M×N, содержит dc << M единиц в
каждом столбце и dr << N единиц в каждой строке. Причем распределение единиц
по столбцам и строкам, в общем случае, случайно. На практике случайное
распределение единиц неудобно – для кодирования и декодирования
необходимо хранить проверочные и генераторные матрицы, что достаточно
накладно при больших длинах кодов.
Очевидным средством борьбы с этой проблемой является переход к кодам LDPC,
проверочная матрица которых обладает какой-то структурой. Простейший вариант
структуризации проверочной матрицы – использование циклических кодов.
Проверочная матрица такого кода представляет собой циркулянтную матрицу
размерности N×N, в которой каждая строка получается циклическим сдвигом
вправо предыдущей строки. Значение влияния цикличности проверочной
матрицы на сложность декодера LDPC кода сложно переоценить, поскольку
каждая из строк матрицы однозначно определяется предыдущей строкой, в связи
с чем реализация декодера может быть существенно упрощена по сравнению со
случайной структурой проверочной матрицы.

27. Классификация кодов, исправляющих ошибки (ЕСС)

Классификация кодов LDPC
К недостаткам циклических кодов можно отнести фиксированный для всех
скоростей кодирования размер проверочной матрицы N×N, что подразумевает
более сложный декодер, а также высокий Хэммингов вес строк, что усложняет
структуру декодера. К достоинствам, помимо упрощения
кодирования/декодирования, следует отнести большое минимальное расстояние
и очень низкий порог при итеративном декодировании.
Желание преодолеть недостатки циклических LDPC кодов привело к появлению
квазициклических LDPC кодов. Квазициклические коды также имеют хорошую
структуру, позволяющую упростить кодер и декодер. В дополнение к этому они
позволяют более гибко подойти к разработке кода, в частности позволяют
синтезировать нерегулярные коды. Проверочная матрица такого кода
представляет собой не что иное, как набор циркулянтных подматриц. Для
получения низкоплотностного кода циркулянтные матрицы должны быть
разреженными, что на практике означает использование в качестве циркулянтов
единичных матриц. Для того чтобы получить нерегулярный код, какие-то
подматрицы просто объявляются нулевыми.
A11 A1N
H
AM 1 AMN

28. Классификация кодов, исправляющих ошибки (ЕСС)

Методы построения проверочных
матриц кодов LDPC
Методы построения LDPC кодов также можно разбить на классы. К первому классу
относятся все алгоритмические способы и способы, использующие
вычислительную технику. А ко второму – способы, основанные на теории графов,
математике конечных полей, алгебре и комбинаторике.
Первый класс методов позволяет получать как случайные, так и
структурированные коды LDPC , в то время как второй нацелен на получение
только структурированных кодов LDPC , хотя бывают и исключения.
В отличие от других линейных блоковых кодов, таких как БЧХ или кодов
Рида‑Соломона, имеющих строгий алгоритм синтеза кодов с заданными
параметрами, для кодов LDPC существует множество способов построения кодов.
Часто используются способы построения LDPC кодов, предложенные Галлагером и
МакКеем. В некоторых стандартах используется более сложный алгоритм
построения достаточно эффективных кодов повторения накопления.

29. Корректирующие коды, используемые в системах ЦТВ

LDPC коды Галлагера
H1
Проверочная матрица кода строится из подматриц Ha, a = 1, …, dc, которые
H
2
имеют структуру, описываемую следующим образом:
H
для любых двух целых μ и dr, больших 1, каждая подматрица Ha имеет
H
размерность μ×μ·dr, при этом веса строк этой подматрицы – dr, а столбцов – 1. d c
Подматрица H1 имеет специфическую форму: для i = 0, 1, …, μ – 1 i-ая строка
содержит все dr единиц на позициях с i от dr до (i + r)·r – 1. Оставшиеся подматрицы
получаются перестановкой столбцов матрицы H1. Очевидно, что результирующая
матрица H – регулярная матрица размерности μ·dc×μ·dr с весами строк и столбцов
dr и dс соответственно.
Важной характеристикой матрицы LDPC кода является отсутствие циклов
определённой кратности. Под циклом кратности 4 понимается наличие в двух
разных столбцах проверочной матрицы ненулевых элементов на совпадающих
позициях. Отсутствие цикла кратности 4 определяется вычислением скалярного
произведения столбцов матрицы: если всевозможные скалярные произведения
всех столбцов матрицы не превосходят 1, то это означает отсутствие в матрице
циклов кратности 4. Цикл кратности 4 является минимально возможным и
встречается существенно чаще циклов большей длины (6, 8, 10 и т. д.).
Присутствие в матрице LDPC кода циклов любой кратности свидетельствует о
заложенной в структуру матрицы избыточности, не приводящей к улучшению
помехоустойчивых свойств кода.

30. Сверочные коды

LDPC коды Галлагера
Пример циклов кратности 4:
Рассмотренный алгоритм не гарантирует отсутствие циклов кратности 4, однако
они могут быть удалены впоследствии. Галлагер показал , что ансамбль таких
кодов обладает прекрасными свойствами. Также была показана возможность
реализации достаточно простых кодеров,
1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0
поскольку проверочные биты такого кода
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0
могут быть найдены по проверочной
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0
матрице кода как функция
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
информационных узлов.
1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0
Проверочная матрица кода
Галлагера (20, 5) dc = 3, dr = 4, μ = 5
имеет следующий вид:
0
H 0
0
0
1
0
0
0
0
1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0
0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0
0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1
1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0
0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0
0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 1 0
0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0
0 0
0 0
0 0
0 0
1 1
0 0
0 0
0 0
1 0
0 1
0 0
0 0
1 0
0 0
0 1

31.

LDPC коды МакКея
Тридцать пять лет спустя МакКей, будучи незнакомым с работой Галлагера,
повторно открыл преимущества кодов с разреженными матрицами. При помощи
компьютерного моделирования он показал возможность этих кодов вплотную
приблизиться к границе Шеннона как для двоичного симметричного канала, так и
для канала с аддитивным белым гауссовским шумом.
МакКей предложил несколько компьютерных алгоритмов построения
проверочных матриц кодов LDPC. Вот некоторые из них в порядке увеличения
сложности реализации:
1. Проверочная матрица H синтезируется путем случайного генерирования
столбцов веса dc и, насколько это возможно, равномерным распределением весов
строк dr.
2. Проверочная матрица H синтезируется путем случайного генерирования
столбцов веса dc и строк веса dr, с дополнительной проверкой на отсутствие
циклов кратности 4.
3. Проверочная матрица H синтезируется по алгоритму 2, с дополнительным
удалением циклов кратности 4.
4. Проверочная матрица H синтезируется по алгоритму 3, с дополнительным
условием, что проверочная матрица имеет вид H = [H1H2], где H2 – обратимая
матрица.
Недостатком алгоритмов МакКея является отсутствие какой-либо структуры в
проверочных матрицах, что усложняет процесс кодирования.

32.

LDPC коды повторения накопления
К настоящему времени разработано достаточно большое количество более
сложных алгоритмов, позволяющих получать коды, обладающие лучшей
эффективностью и хорошо структурированной проверочной матрицей.
В стандарте DVB‑T2 используется систематический нерегулярный код повторениянакопления (irregular repeat accumulate – IRA). IRA коды – это класс LDPC кодов,
разработанный на основе кодов повторения-накопления (repeat accumulate – RA).
Отличительными особенностями этого класса кодов является возможность
использования алгоритмов кодирования по проверочной матрице, а также
возможность использования компактных форм хранения самих проверочных
матриц.
Граф Таннера для IRA кода изображают в необычной форме,
для этих кодов битовые узлы удобно разбить на
информационные узлы (information nodes – IN) и узлы
четности (parity nodes – PN). На рис. изображен граф Таннера
для кода повторения-накопления, битовые узлы обозначены
кругами, а проверочные – квадратами; битовые узлы,
расположенные слева – информационные, поскольку
соответствуют исходным битам, требующим кодирования, а
расположенные справа – узлы четности PN, они соответствуют
полученным в результате кодирования проверочным битам.

33.

LDPC коды повторения накопления
Код DVB‑T2 является нерегулярным – степени символьных вершин переменные, в
то время как степени кодовых вершин одинаковы (исключение составляет только
самый первый кодовый узел, степень которого на единицу меньше).
Для описания распределения степеней информационных вершин IRA кода
вводится ряд распределения (f1, …, fJ), где fi обозначает долю информационных
узлов, соединенных с i проверочными узлами, fi ≥ 0, Sum(fi) = 1. Каждый
проверочный узел соединен с a информационными узлами и полная запись
параметров IRA кода имеет вид (f1, …, fJ; a).
Слева расположены K информационных узлов, по
середине и справа – M проверочных узлов и узлов
четности соответственно. Каждый проверочный узел
соединяется ровно с a информационными узлами, это
соединение может быть описано при помощи матрицы
случайных перестановок M×a ребер. Соединение узлов
четности с проверочными изображено зигзагообразной
линией.

34. Декодирование сверточных кодов Алгоритм Витерби

LDPC коды повторения накопления
Из структуры рассмотренного графа Таннера видно, что проверочную матрицу
кода можно представить в виде двух подматриц H = [HuHp].
Подматрица Hu размерности M×K – разреженная матрица, а подматрица Hp,
размерности M×M – ступенчатая матрица, которой на рис. соответствует ломаная
линия, соединяющая проверочные узлы с узлами четности.
Кодирование линейных блоковых кодов осуществляется при помощи
генераторной матрицы, которую, в свою очередь, можно получить по
проверочной. Генераторная матрица,
соответствующая
данной проверочной
T
T
1 1
матрице H, имеет вид: G ( I HT u H p )
1 1
H u не представляет особого труда,
При этом получение
матрицы
T
T
H p
а подматрица H p генераторной матрицы G для IRA кода
1
является верхней треугольной матрицей.
1
1
1
1

35.

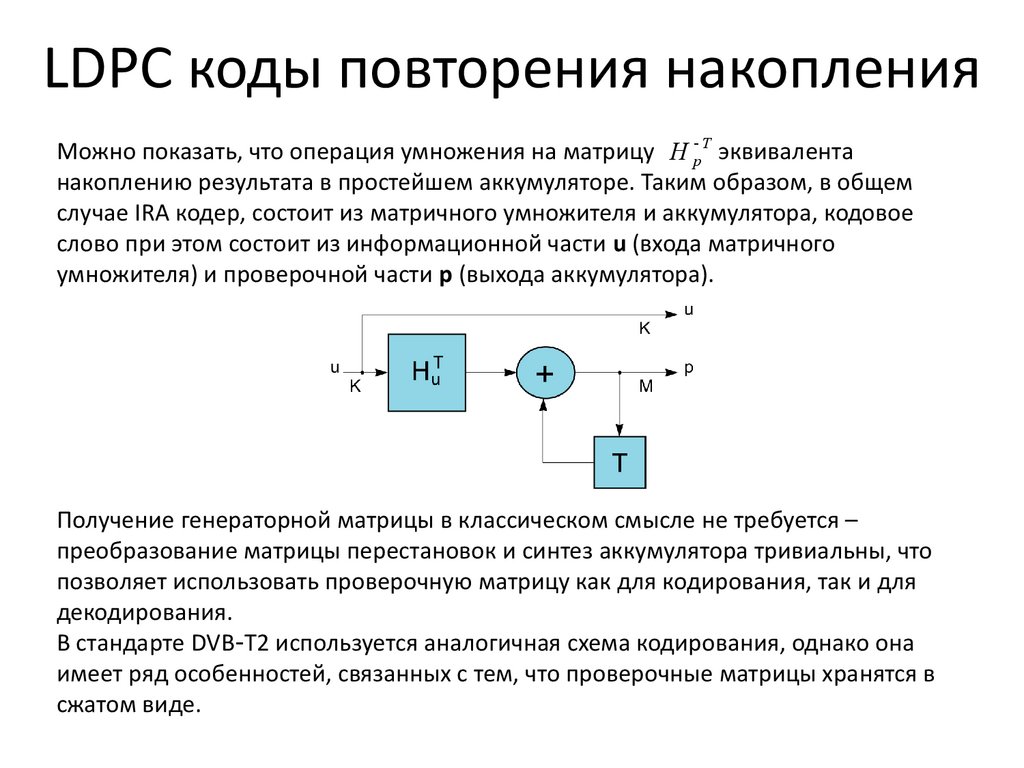
LDPC коды повторения накопления
Можно показать, что операция умножения на матрицу H p T эквивалента
накоплению результата в простейшем аккумуляторе. Таким образом, в общем
случае IRA кодер, состоит из матричного умножителя и аккумулятора, кодовое
слово при этом состоит из информационной части u (входа матричного
умножителя) и проверочной части p (выхода аккумулятора).
Получение генераторной матрицы в классическом смысле не требуется –
преобразование матрицы перестановок и синтез аккумулятора тривиальны, что
позволяет использовать проверочную матрицу как для кодирования, так и для
декодирования.
В стандарте DVB‑T2 используется аналогичная схема кодирования, однако она
имеет ряд особенностей, связанных с тем, что проверочные матрицы хранятся в
сжатом виде.

36.

LDPC коды DVB-T2
Используемые в DVB-T2 проверочные матрицы LDPC кода, помимо того, что они
описывают IRA код, имеют некоторую периодичность в структуре, что позволяет
существенно упросить их хранение, а также позволяет получить эффективную
архитектуру декодеров таких кодов.
Способ построения матрицы Hu заключается в делении информационных узлов на
группы по Q узлов в каждой, причем все узлы группы должны иметь одинаковую
степень. При этом для того, чтобы однозначно определить схему соединения всех
Q информационных узлов с проверочными узлами, достаточно указать только те
проверочные узлы, которые соединены с первым информационным узлом в
рассматриваемой группе.
Обозначим как c1 , c2 , ..., cwl индексы проверочных узлов, соединенных с первым
информационным узлом в группе, тогда индексы проверочных узлов любого i-го
информационного узла в группе можно получить, воспользовавшись формулами:
[c1 (i 1)q] mod(n k ),
[c 2 (i 1)q ] mod(n k ),
[c wl (i 1)q ] mod(n k ),
где q = (n – k)/Q.

37. DVB-S – внутреннее кодирование

LDPC коды DVB-T2
Для полного описания структуры матрицы используемого кода необходимо
указать проверочные узлы, соединенные с первым информационным узлом в
каждой из групп. Код стандарта DVB‑T2 предусматривает использование
фиксированного размера групп для всех скоростей и размеров блоков – это
Q = 360 битовых узлов, число групп в матрице будет отличаться для различных
скоростей и размеров блоков. В стандарте приводятся таблицы, в которых
перечисляются проверочные узлы для первого битового узла каждой из групп для
всех скоростей кодирования и используемых блоков передачи данных.
Пример таблицы для короткого блока (N = 16200) со скоростью кодирования 2/3
представляет собой запись матрицы размерности 10800×16200 и имеет
следующий вид:
0 2084 1613 1548 1286 1460 3196 4297 2481 3369 3451 4620 2622
1 122 1516 3448 2880 1407 1847 3799 3529 373 971 4358 3108
2 259 3399 929 2650 864 3996 3833 107 5287 164 3125 2350
3 342 3529
1 2583 1180
4 4198 2147
2 1542 509
5 1880 4836
3 4418 1005
6 3864 4910
4 5212 5117
7 243 1542
5 2155 2922
8 3011 1436
6 347 2696
9 2167 2512
7 226 4296
10 4606 1003
8 1560 487
11 2835 705
9 3926 1640
12 3426 2365
10 149 2928
13 3848 2474
11 2364 563
14 1360 1743
12 635 688
0 163 2536
13 231 1684
14 1129 3894

38. Схема сверточного кодера

Декодирование кодов LDPC
Р. Галлагер предложил два итеративных алгоритма декодирования кодов LDPC.
Первый – алгоритм с распространением доверия (belief propagation, BP). Этот
алгоритм обладает максимальной эффективностью среди всех известных
алгоритмов декодирования. Доказано, что алгоритм BP достигает максимума
правдоподобия, при условии, что проверочная матрица кода не содержит циклов.
Расплата за столь высокую эффективность – максимальная вычислительная
сложность среди всех известных алгоритмов.
Второй алгоритм, предложенный Р. Галлагером, – алгоритм с инверсией бита (bit
flip algorithm, BF). Он очень прост в реализации и использует жесткие решения
модема относительно принятых бит. Расплата за простоту – низкая эффективность
этого алгоритма. Оба алгоритма в настоящее время хорошо исследованы и для
них разработано множество модификаций. Также существует и множество
альтернативных оригинальных алгоритмов декодирования LDPC кодов.

39. Сверточный кодер, M=4, N=2

Декодирование кодов LDPC - BF
Алгоритм BF можно представить в виде основных шагов, выполняемых
итеративно:
- инициализация,
- обновление проверочных узлов,
- обновление битовых узлов,
- инверсия бит.
Первый шаг алгоритма – инициализация – выполняется только один раз для
каждого кодового слова. Суть ее заключается в вынесении жестких решений
относительно принятых бит: xn = sing(yn), n = 1, …, N, xn – жесткие решения модема
dr
относительно принятых бит yn.
Второй шаг – обновление проверочных узлов m xni mod 2 ,
i 1
xni - входящие в проверочный узел m сообщения,
σm – исходящее из этого проверочного узла сообщение,
dr – количество смежных битовых узлов.
Здесь xn – по существу не что иное, как знак принятого из
канала значения, полученный на этапе инициализации.
В случае алгоритма с инверсией бита исходящее сообщение
σm может принимать всего два значения – 0 или 1, что,
в свою очередь, показывает, выполняется соответствующая
проверка или нет.

40.

Декодирование кодов LDPC - BF
dc
Третий шаг алгоритма – обновление битовых узлов: Z n mi ,
i 1
Zn – исходящее из битового узла n сообщение,
σmi – входящие в этот битовый узел сообщения,
dc – количество смежных проверочных узлов.
В случае алгоритма с инверсией бита значение исходящего сообщения Zn равно
числу невыполненных проверок для битового узла n. После того как найдены
значения Zn для всех битовых узлов, находится и инвертируется бит, для которого
Zn максимально.
Алгоритм является очень простым, а, следовательно, очень быстрым, однако
эффективность этого алгоритма существенно ниже алгоритма BP. Другим
существенным недостатком этого алгоритма является его медленная сходимость,
особенно для блоков большой длины. В силу указанных недостатков этот алгоритм
практически не используется.

41.

Декодирование кодов LDPC - BP
Алгоритм BP можно представить в виде следующих шагов:
- инициализация,
- обновление проверочных узлов,
- обновление битовых узлов,
- вынесение жестких решений.
Последние три шага выполняются итеративно.
Инициализация алгоритма: Znmi – сообщения от битового узла n
к соответствующему проверочному узлу mi, rn – логарифмическое
отношение правдоподобия (log likelihood ratio, LLR) для битового
узла n.
Второй шаг алгоритма – обновление проверочных узлов:
Znim – входящие сообщения для проверочного узла m
от dr смежных битовых узлов,
ynim – исходящие сообщения от узла m
к битовым узлам ni. Исходящие сообщения рассчитываются
по следующей формуле: ynim g ( Z n1m ,..., Z ni 1m , Z nn 1m ,..., Z ndr m )
g (a, b) sign(a) sign(b) min(| a |, | b |) LUTg (a, b)
LUTg (a, b) log(1 e |a b| ) log(1 e |a b| )

42.

Декодирование кодов LDPC - BP
Третий шаг – обновление битовых узлов:
ynmi – входящие сообщения для битового узла n от dc смежных
проверочных узлов, Znmi – исходящие сообщения для каждого
d c узла m .
проверочного
i
Z nmi | rn | y nm j
j i
После обновления всех битовых узлов находятся жесткие оценки
принятых
бит,
представляют собой нечто иное, как знак Zn:
Z n Z nmi
y nmкоторые
i
Если все проверки выполняются при подстановке в них жестких оценок принятых
бит, это значит, что в результате декодирования найдено допустимое кодовое
слово. При этом вычисления прекращаются, а найденное кодовое слово считается
результатом декодирования. В противном случае выполняется еще одна итерация
обновления проверочных и битовых узлов. В случае если достигнуто
максимальное заданное число итераций декодирования, а допустимое кодовое
слово не найдено, то вычисления прекращаются, а текущее кодовое слово
считается результатом декодирования.
К недостаткам алгоритма BP относятся высокая сложность реализации, а также
необходимость оценки отношения сигнал/шум на входе приемника для расчета
логарифмических отношений правдоподобия.

43.

Декодирование кодов LDPC
На рис. изображены зависимости
вероятности битовой ошибки от
отношения сигнал шум для
рассмотренных алгоритмов
декодирования. Результаты приведены
для кода скорости 3/4 и размерности
64800 стандарта DVB-T2, число
итераций декодирования для всех
алгоритмов равно 20.