Выведение формулы золотого сечения

1. Выведение формулы золотого сечения

Выполнил:
Курютин
Алексей,
12 группа

2. Пифагор Самосский

Пифагор — древнегреческий философ, математик и мистик. Родился
в 570 году до н. э. на острове Самосе. Именно ему принадлежит
известная «теорема квадратов» и модель Солнечной системы,
основанная на аналогии в расположении планет и звуков
музыкальной октавы.
Бюст Пифагора
в
Капитолийском
музее в Риме

3. «Золотой треугольник»

В простейшем прямоугольном треугольнике с
соотношением катетов 1:2 по теореме Пифагора
длина гипотенузы равна √5.
Число «пять» у пифагорейцев считалось священным .
Соотношения сторон a, b, c данного треугольника: a/b=1:2, c/a=√5/1, c/b=√5/2,из них
следует ещё одно соотношение (a+c)/b; равное 1,618033, которое и является Золотой
пропорцией. Чаще её обозначают буквой Ф.
Таким образом, хорошо известный в древнем мире простой прямоугольный треугольник с
отношением катетов 1:2 мог послужить основой для открытия теоремы квадратов, золотой
пропорции и несоизмеримых величин — великих открытий Пифагора.

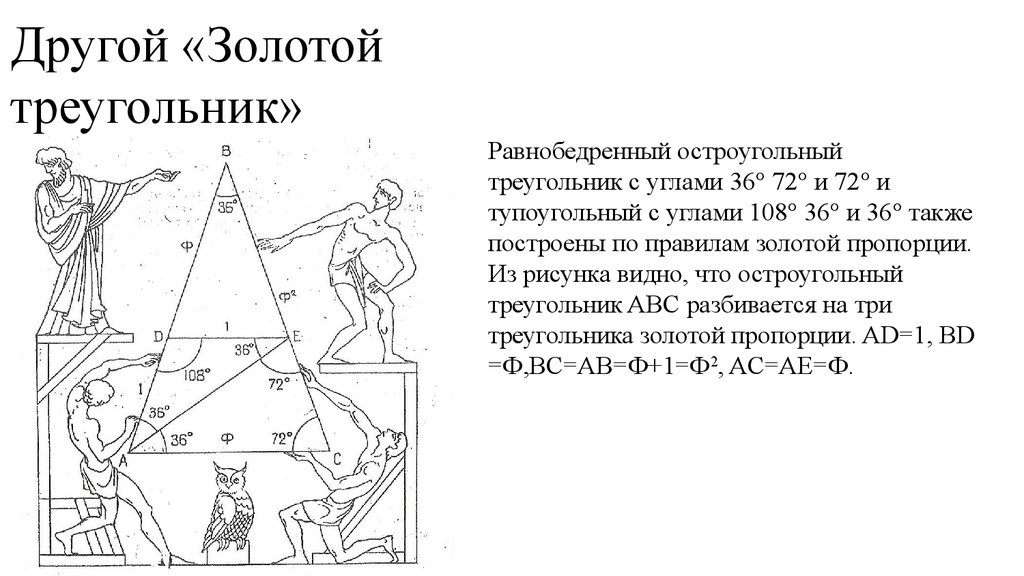
4. Другой «Золотой треугольник»

Равнобедренный остроугольный
треугольник с углами 36° 72° и 72° и
тупоугольный с углами 108° 36° и 36° также
построены по правилам золотой пропорции.
Из рисунка видно, что остроугольный
треугольник ABC разбивается на три
треугольника золотой пропорции. AD=1, BD
=Ф,BC=AB=Ф+1=Ф2, AC=AE=Ф.

5. Связь с числом π

Также интересен п/у треугольник с углами 90° 54° 36°, и в нём тоже проявляется
золотая пропорция. Отношение углов составляет 5:3:2. В нём отношение большего
катета к гипотенузе равна половине золотой пропорции Ф/2. Отсюда вытекает
формула связывающая золотую пропорцию с числом π: Ф=(√5 +1)/2=2Cos π/5.
В той формуле дважды встречается чило «пять». И угол 36° является углом при
вершинах пятиконечного звёздчатого многоугольника

6. Ряд чисел Фибоначчи

Появился он в ходе решения задачи из книги «Liber abacci»,
написанной самим Леонардо Фибоначчи. Вопрос в задаче был
“Сколько пар кроликов в один год от одной пары рождается”. И
только через 500 лет англ. уч. Р. Симпсон строго доказал, что
отношение рядом расположенных чисел Фибоначчи в
пределестремится к золотой пропорции равной (√5+1)/2.
Леонардо Пизанский
Фибоначчи

7.

Инвариантом золотого сечения явился ряд чисел Фибоначчи 1, 2, 3, 5, 8, 13, 21, 34 и
т. д., где каждое последующее число является суммой двух предыдущих чисел,
называется Рядом чисел Фибоначчи. В математике это записывается следующим
образом:
U1, U2 , U3, где Un= Un-1+ Un-2.

8. Ряд Люка