Inverzná kinematika – aprox. metóda

1. Inverzná kinematika – aprox. metóda

Newtonová aproximačná metóda
s použitím Jacobyho matice:
df1
dx1
df 2
J dx
1
df m
dx
1
df1
dx2
df 2
dx2
df m
dx2
df1
dxn
df 2
dxn
df m
dxn
dq J 1dp
s J 1 ( ( DP TP))
J ( DK ( , , , , , )) ( DK ( , , , , , )) ( DK ( , , , , , ))
( DK ( , , , , , )) ( DK ( , , , , , )) ( DK ( , , , , , ))

2. Algoritmus inverznej kinematiky

Vstupy: počiatočný stav, požadovaná poloha,
parameter Δ.
Volaná funkcia: Priama kinematika
Výstup: natočenie kĺbov a počet iterácií

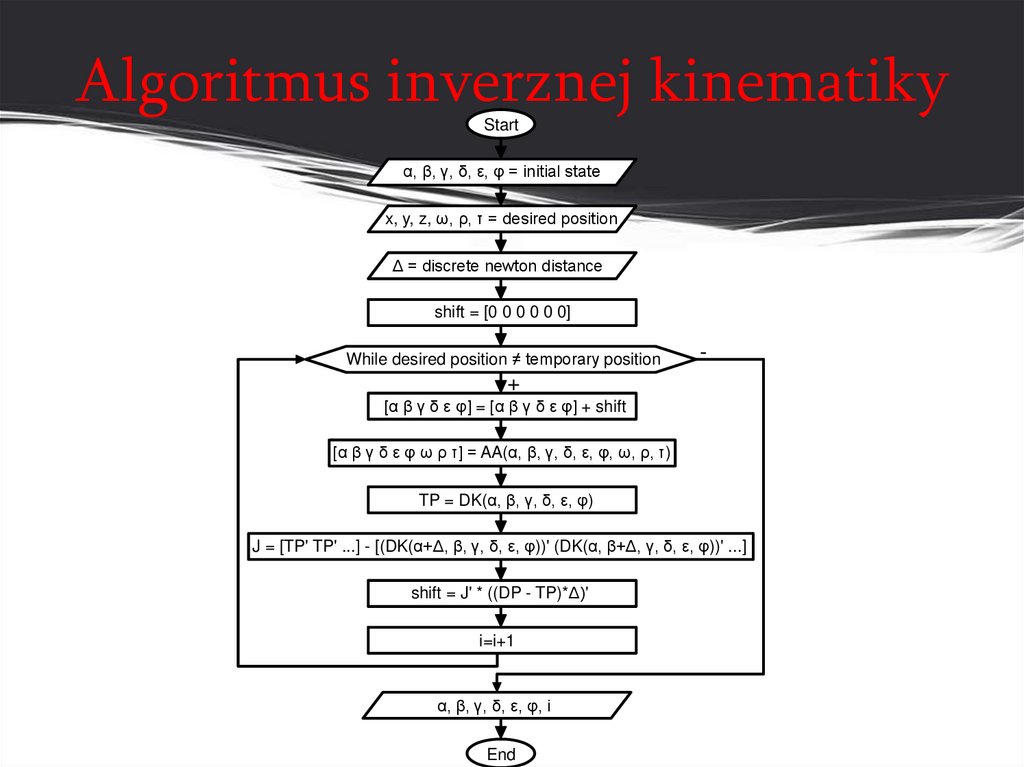
3. Algoritmus inverznej kinematiky

Start
α, β, γ, δ, ε, φ = initial state
x, y, z, ω, ρ, τ = desired position
Δ = discrete newton distance
shift = [0 0 0 0 0 0]
While desired position ≠ temporary position
-
+
[α β γ δ ε φ] = [α β γ δ ε φ] + shift
[α β γ δ ε φ ω ρ τ] = AA(α, β, γ, δ, ε, φ, ω, ρ, τ)
TP = DK(α, β, γ, δ, ε, φ)
J = [TP' TP' ...] - [(DK(α+Δ, β, γ, δ, ε, φ))' (DK(α, β+Δ, γ, δ, ε, φ))' ...]
shift = J' * ((DP - TP)*Δ)'
i=i+1
α, β, γ, δ, ε, φ, i
End

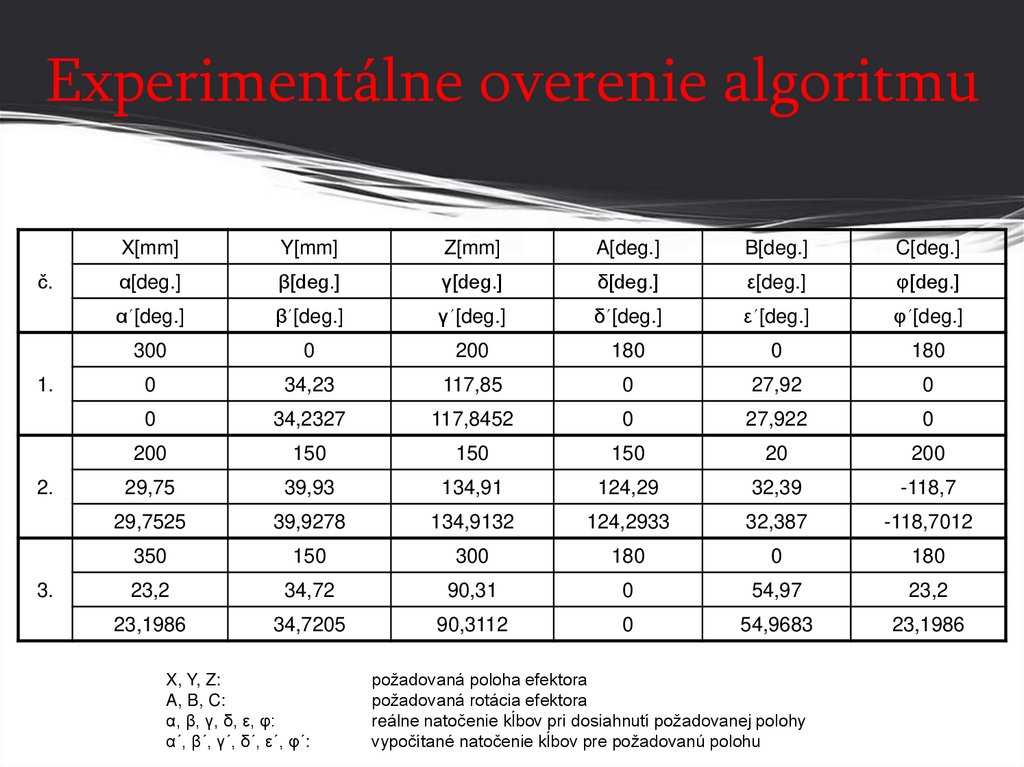
4. Experimentálne overenie algoritmu

č.
1.
2.
3.
X[mm]
Y[mm]
Z[mm]
A[deg.]
B[deg.]
C[deg.]
α[deg.]
β[deg.]
γ[deg.]
δ[deg.]
ε[deg.]
φ[deg.]
α´[deg.]
β´[deg.]
γ´[deg.]
δ´[deg.]
ε´[deg.]
φ´[deg.]
300
0
200
180
0
180
0
34,23
117,85
0
27,92
0
0
34,2327
117,8452
0
27,922
0
200
150
150
150
20
200
29,75
39,93
134,91
124,29
32,39
-118,7
29,7525
39,9278
134,9132
124,2933
32,387
-118,7012
350
150
300
180
0
180
23,2
34,72
90,31
0
54,97
23,2
23,1986
34,7205
90,3112
0
54,9683
23,1986
X, Y, Z:
A, B, C:
α, β, γ, δ, ε, φ:
α´, β´, γ´, δ´, ε´, φ´:
požadovaná poloha efektora
požadovaná rotácia efektora
reálne natočenie kĺbov pri dosiahnutí požadovanej polohy
vypočítané natočenie kĺbov pre požadovanú polohu