Рекурсия и рекурсивные алгоритмы

1. Рекурсия и рекурсивные алгоритмы

2. Рекурсия в жизни

Рекурсия – это определение объекта
посредством ссылки на себя.
Жил-был царь.
У царя – двор.
На дворе мочало –
Начинай сначала!

3. Рекурсия в программировании

Рекурсивным называют алгоритм, в описании
которого прямо или косвенно содержится
обращение к самому себе.
Рекурсивная функция - это функция, которая
вызывает саму себя.
Например, вычисление факториала
чисел Фибоначчи и наибольшего общего
делителя с помощью алгоритма Эвклида

4. Особенности рекурсий

• Рекурсия – это приём, позволяющий свести исходную
задачу к одной или нескольким более простым задачам
того же типа.
• Рекурсия показывает закономерность прохождения
события.
• Для того, чтобы определить рекурсию, нужно задать:
- рекуррентную формулу
- условие остановки рекурсии.
• Любую рекурсию можно запрограммировать с
помощью цикла.
• Рекурсия позволяет заменить цикл и в некоторых
сложных задачах делает решение более понятным, хотя
часто менее эффективным.

5. Виды рекурсий

Прямая
• Вызов одной функции с изменяющимся
набором параметров
• Например, вычисление факториала числа
Косвенная
• Содержит вызовы других функций из своего тела, при
этом возможен вызов начальной функции с
измененным набором входных параметров
• Например, нахождение наибольшего общего
делителя

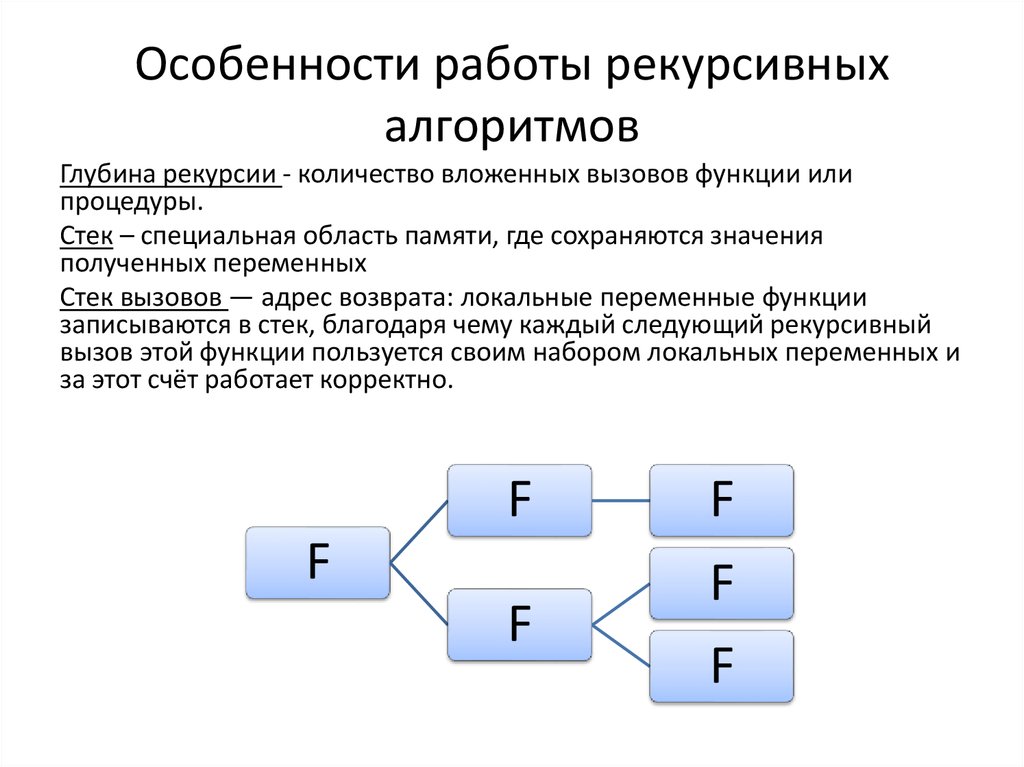
6. Особенности работы рекурсивных алгоритмов

Глубина рекурсии - количество вложенных вызовов функции или
процедуры.
Стек – специальная область памяти, где сохраняются значения
полученных переменных
Стек вызовов — адрес возврата: локальные переменные функции
записываются в стек, благодаря чему каждый следующий рекурсивный
вызов этой функции пользуется своим набором локальных переменных и
за этот счёт работает корректно.
F
F
F
F
F
F

7. Использование рекурсий

При компьютерном моделировании задач из различных
предметных областей.

8. Решение задач, головоломок

Задача Ханойская башня.
Даны три стержня, на один из которых нанизаны
восемь колец, причем кольца отличаются размером и
лежат меньшее на большем. Задача состоит в том,
чтобы перенести пирамиду из восьми колец за
наименьшее число ходов на другой стержень. За один
раз разрешается переносить только одно кольцо,
причём нельзя класть большее кольцо на меньшее.