Логические законы и правила преобразования логических выражений

1. Логические законы и правила преобразования логических выражений.

Учитель информатики и ИКТ
ГБОУ Лицея 1561 г. Москвы
Кондрухова Ольга Васильевна

2. Тест

1. По таблице истинности
определить логическую
функцию:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
А
И
И
Л
Л
В
И
Л
И
Л
?
И
И
И
Л

3. Тест

2. По таблице истинности
определить логическую
функцию:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
А
И
И
Л
Л
В
И
Л
И
Л
?
И
Л
Л
И

4. Тест

3. По таблице истинности
определить логическую
функцию:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
А
И
И
Л
Л
В
И
Л
И
Л
?
И
Л
Л
Л

5. Тест

4. По таблице истинности
определить логическую
функцию:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
А
И
И
Л
Л
В
И
Л
И
Л
?
И
Л
И
И

6. Тест

5. По таблице истинности
определить логическую
функцию:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
А
И
Л
?
Л
И

7. Тест

6. Покажите порядок
выполнения логических
операций в выражении:
а)
, , , ;
б)
, , , ;
в)
, , , ;
г)
, , , .
X (Y C ) Z

8. Тест

7. Дано: А – Виноград зеленый,
В – Виноград сладкий.
Найти логическую схему для
высказывания:
а)
б)
A B;
A B;
в)
A B;
г)
A B.
«Если виноград
зеленый, то он не
сладкий»

9. Тест

8. Какая логическая функция
имеет следующие
обозначения:
а) конъюнкция;
б) дизъюнкция;
в) инверсия;
г) импликация;
д) эквивалентность.
, *, &, and ?

10. Проверьте себя по ключу:

1.
2.
3.
4.
5.
6.
7.
8.
б
д
а
г
в
б
в
а

11. Основные законы алгебры логики

Переместительный(коммутативный)закон:
для логического умножения:
Х Y Y X
в обычной алгебре:
x* y y*x

12. Основные законы алгебры логики

Переместительный(коммутативный)закон:
для логического сложения:
X Y Y X
в обычной алгебре:
x y y x

13. Основные законы алгебры логики

Сочетательный (ассоциативный) закон:
для логического умножения:
X (Y Z ) ( X Y ) Z
в обычной алгебре:
x * ( y * z) ( x * y) * z

14. Основные законы алгебры логики

Сочетательный (ассоциативный) закон:
для логического сложения:
X (Y Z ) ( X Y ) Z
в обычной алгебре:
x ( y z) ( x y) z

15. Основные законы алгебры логики

Распределительный (дистрибутивный) закон:
для логического умножения:
X (Y Z ) ( X Y ) ( X Z )
в обычной алгебре:
x * ( y z) x * y x * z

16. Основные законы алгебры логики

Распределительный (дистрибутивный) закон:
для логического сложения:
X (Y Z ) ( X Y ) ( X Z )
в обычной алгебре аналога нет

17. Основные законы алгебры логики

Законы де Моргана:
для логического умножения:
X Y X Y
отрицание одновременной истинности

18. Основные законы алгебры логики

Законы де Моргана:
для логического сложения:
X Y X Y
отрицание вариантов вместе

19. Основные законы алгебры логики

Законы идемпотентности (повторения):
для логического умножения:
X X X
отсутствие степеней

20. Основные законы алгебры логики

Законы идемпотентности (повторения):
для логического сложения:
X X X
отсутствие коэффициентов

21. Основные законы алгебры логики

Законы поглощения:
для логического умножения:
X (X Y ) X

22. Основные законы алгебры логики

Законы поглощения:
для логического сложения:
X ( X Y ) X

23. Основные законы алгебры логики

Законы склеивания:
для логического умножения:
(X Y ) (X Y ) Y

24. Основные законы алгебры логики

Законы склеивания:
для логического сложения:
( X Y ) ( X Y ) Y

25. Основные законы алгебры логики

Закон противоречия:
для логического умножения:
X X 0

26. Основные законы алгебры логики

Закон исключения третьего:
для логического сложения:
X X 1
Из двух противоречивых высказываний об
одном и том же предмете одно всегда
истинно, а второе – ложно, третьего не дано.

27. Основные законы алгебры логики

Законы исключения констант:
для логического умножения:
X 1 X
X 0 0

28. Основные законы алгебры логики

Законы исключения констант:
для логического сложения:
X 1 1
X 0 X

29. Основные законы алгебры логики

Закон двойного отрицания:
X X
Двойное отрицание исключает отрицание

30. Задание 1

Проведите доказательство
закона поглощения

31.

X (X Y ) X
X
Y
X Y
И
И
И
И
И
Л
И
И
Л
И
И
Л
Л
Л
Л
Л
X
(X Y)

32. Задание 2. Упростить выражение:

X Y X Y
Воспользуемся распределительным законом:
X (Y Z ) ( X Y ) ( X Z )
X Y X Y X (Y Y ) X 1
1
X

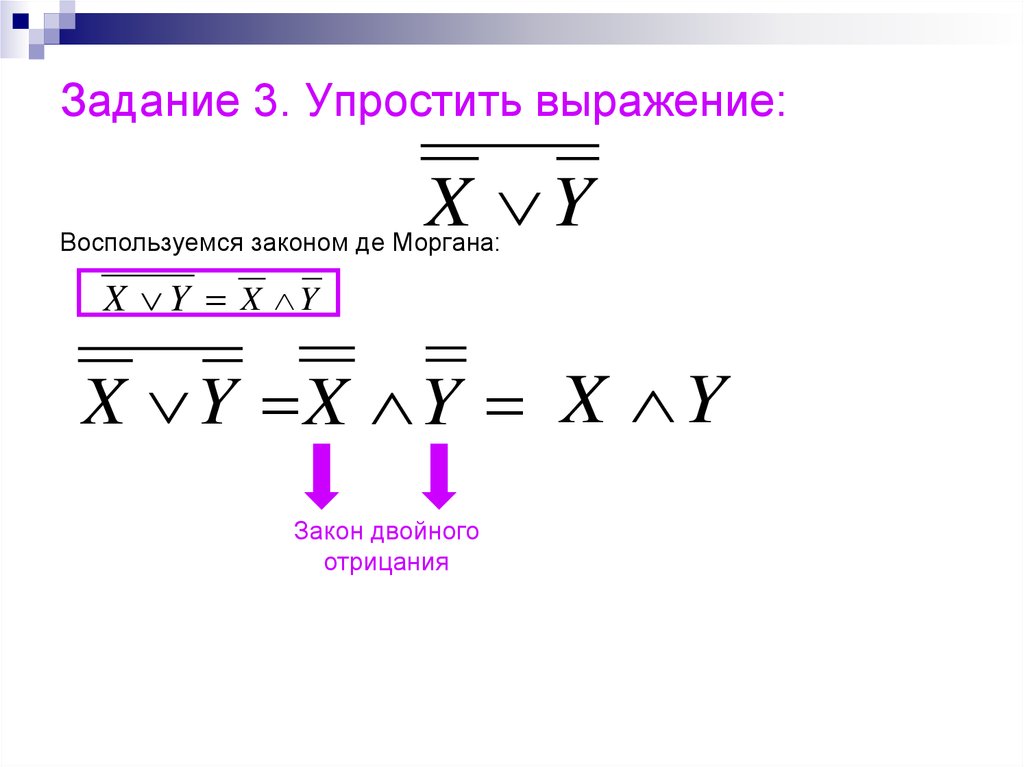
33. Задание 3. Упростить выражение:

X Y
Воспользуемся законом де Моргана:
X Y X Y
X Y X Y X Y
Закон двойного
отрицания