Анализ работы алгоритмов квадратичной сложности

1. Анализ работы алгоритмов квадратичной сложности

Автор: Мосякин Владимир(АИ-181)

2. Что такое «квадратичная сложность»?

Любой алгоритм сортировки, очевидно, требует какое-то время для того,
чтобы корректно обработать все данные. Данное время, зачастую, можно
предсказать по строго определенным формулам.
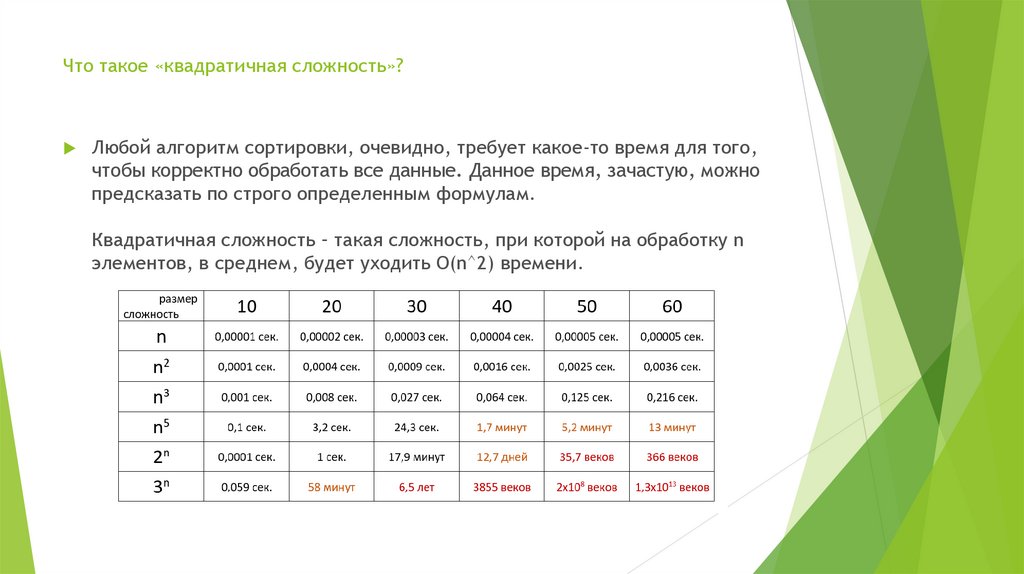
Квадратичная сложность – такая сложность, при которой на обработку n
элементов, в среднем, будет уходить O(n^2) времени.

3. Разница алгоритмов

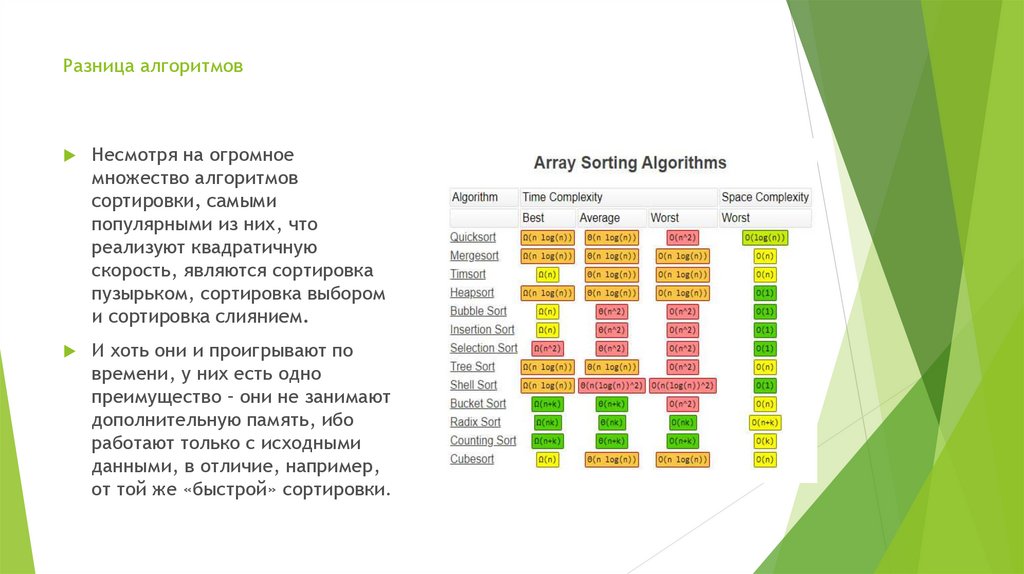
Несмотря на огромное
множество алгоритмов
сортировки, самыми
популярными из них, что
реализуют квадратичную
скорость, являются сортировка
пузырьком, сортировка выбором
и сортировка слиянием.
И хоть они и проигрывают по
времени, у них есть одно
преимущество – они не занимают
дополнительную память, ибо
работают только с исходными
данными, в отличие, например,
от той же «быстрой» сортировки.

4. Сортировка пузырьком

Самый «классический» и
популярный вариант
сортировок. Для понимания
и реализации этот
алгоритм — простейший, но
эффективен он лишь для
небольших
массивов. Алгоритм
считается учебным и
практически не
применяется вне учебной
литературы, вместо него на
практике применяются
более эффективные
алгоритмы сортировки.

5. Сортировка выбором

Может быть как
устойчивый, так и
неустойчивый. На массиве
из n элементов имеет
время выполнения в
худшем, среднем и
лучшем случае O(n^2),
предполагая что
сравнения делаются за
постоянное время.
Уникальность состоит, как
можно заметить, в том,
что он в любом случае
будет работать O(n^2)
времени.

6. Сортировка слиянием

Эта сортировка — хороший
пример использования
принципа «разделяй и
властвуй». Сначала задача
разбивается на несколько
подзадач меньшего
размера. Затем эти задачи
решаются с
помощью рекурсивного
вызова или
непосредственно, если их
размер достаточно мал.
Наконец,
их решения комбинируются,
и получается решение
исходной задачи.

7. Реализация

Для реализации был
выбрал язык Python. Он
хорошо подходит для
работы с большим
количеством входящих
данных, а из-за простого
синтаксиса, написание
кода тоже не составило
особых проблем.
Списки заполняются
каждый раз случайно,
используя метод
random.randint, который
позволяет не задумываться
над тем, какое значение
дальше вписывать

8. Пример

Учитывая то, что в работе
присутствует таймер, после
сортировки определенным
способом, можно увидеть,
сколько времени она заняла.
В данном случае, мы
наблюдаем идентичное
время у пузырькового
метода и метода вставок, и
крайне похожее время у
метода выбором – что,
собственно, и требовалось
доказать – время O(n^2).

9. Спасибо за внимание!