Расстояние между объектами и мера близости

Расстояние между объектами и мера близости (продолжение)

579.58K

Category:

sociology

Методы многомерной классификации

1. Методы многомерной классификации

Тема 4. Кластерный анализ
Тема 5. Дискриминантный анализ.

2. Основные понятия

Классификация – разделение рассматриваемой
совокупности
объектов
или
явлений
на
однородные, в определенном смысле, группы либо
отнесение каждого объекта (из заданного
множества) к одному из заранее известных
классов.
2

3.

Пусть каждый i-ый из анализируемых объектов
(i 1, n) характеризуется значениями определенного набора
(1)
( 2)
( p)
признаков (свойств) x i , x i , , xi
, т.е. речь идет о
классификации многомерных наблюдений x1 , x2 , , xn , где
(1)
( p)
xi ( xi , , xi )T - в-р столбец значений признаков для
i-го объекта.
2. Обучающие выборки X j1 , X j 2 , , X jn , j = 1, 2,…, k,
каждая (j-ая) из которых определяет значения анализируемых
(1)
( 2)
( p)
признаков X ji ( x ji , x ji , , x ji )T на n объектах, о которых
априори известно, что они принадлежат j-му классу, причем
число k различных выборок равно общему числу всех
3
возможных классов.
1.

4. Результат

1. если число классов k и их смысл известны заранее, то
каждое из n классифицируемых многомерных наблюдений
должно быть снабжено «адресом» (номером) класса, к
которому оно принадлежит.
или
2. если число классов k и (или) их смысл выявляются в
процессе классификации, то результатом классификации
является разделение множества классифицируемых
объектов
на определенное число однородных
(в определенном смысле) групп, каждая из которых
объявляется классом.
4

5.

Если
в
начале
располагают
не
только
классифицируемыми данными, но и обучающими
выборками, то имеем задачу классификации при
наличии обучающих выборок или «классификации с
обучением» (методы дискриминантного анализа);
в противном случае – задача «классификации без
обучения» (методы кластерного анализа).
5

6. Кластерный анализ

Постановка задачи.
Пусть исследуется совокупность n объектов, каждый
из которых характеризуется по k замеренным на нем
признакам X.
Требуется разбить эту совокупность на однородные в
некотором смысле группы (классы).
Полученные в результате разбиения группы обычно
называются кластерами.
6

7. Расстояние между объектами и мера близости

Понятие однородности объектов
задается либо введением правила вычисления
расстояния
ρ(Xi,Xj)
между
любой
парой
исследуемых объектов (X1,X2,…,Xn), либо заданием
некоторой
функции
r(Xi,Xj),
характеризующей
степень близости i-го и j-го объектов.
7

8.

x2
12
4
1
10
5
8
2
3
6
4
2
0
0
2
4
6
8
10
12
14
x1
8

9. Расстояние между объектами и мера близости

обычное евклидово расстояние;
Е (X i , X j )
k
2
(
x
x
)
il jl
l 1
xil – значение l-го признака у i-го объекта.
Для приведения признаков к одинаковым единицам
прибегают к нормировке каждого признака:
x
Н
il
xil xl
l
9

10. Расстояние между объектами и мера близости (продолжение)

«взвешенное» евклидово расстояние;
ВЕ ( X i , X j )
k
2
w
(
x
x
)
l il jl
l 1
Каждой компоненте xl вектора X приписывают
некоторый вес wl, учитывающий степень важности
данного признака в задаче классификации.
Обычно полагают 0 ≤ wl ≤ 1, где l = 1, 2, …, k.
10

11. Расстояние между объектами и мера близости (продолжение)

хеммингово расстояние;
k
H ( X i , X j ) | xil x jl |
l 1
Используется как мера различия объектов,
задаваемых
дихотомическими
признаками.
Хеммингово расстояние равно числу несовпадений
значений
соответствующих
признаков
в
рассматриваемых i-ом и j-ом объектах.
11

12. Расстояние между кластерами

Пусть Si – i-я группа (кластер), состоящая из ni
объектов.
Способы
вычисления
расстояния
между
кластерами:
1. расстояние по принципу «ближайшего соседа»:
min ( Sl , S m ) min xi , x j
xi S l
x j Sm
12

13. Расстояние между кластерами

2. расстояние по принципу «дальнего соседа»:
max ( Sl , S m ) max xi , x j
xi S l
x j Sm
3.
расстояние между центрами тяжести классов
(Sl , Sm ) xl , x m
1
где x l
nl
x
i
- «центр тяжести» l-ой группы.
xi S l
13

14. Расстояние между кластерами

4. расстояние по принципу «средней связи»:
1
ср (Sl , Sm )
nl nm xi Sl
x , x
i
j
x j S m
- среднее арифметическое всех попарных расстояний
между представителями рассматриваемых групп.
14

15. Иерархические процедуры классификации

позволяют
получить представление о структуре классифицируемой
совокупности наблюдений в форме дендрограммы.
Различают
агломеративные
и
дивизимные
иерархические процедуры классификации .
15

16. Иерархические процедуры классификации

Агломеративные
иерархические
процедуры
классификации на первом шаге рассматривают каждое
из классифицируемых наблюдений
xi (i 1, n)
как
отдельный кластер.
Далее
на
каждом
шаге
алгоритма
происходит
объединение двух самых близких наблюдений, затем –
двух самых близких групп наблюдений (кластеров).
Работа алгоритма заканчивается, когда все исходящие
наблюдения оказались объединенными в один класс.
16

17. Иерархические процедуры классификации

ПРИМЕР
По приведенным данным провести классификацию
5 семей по двум показателям: уровень расходов за
летние месяцы на культурные нужды, спорт и отдых
(x1), уровень расходов на питание (x2).
№ семьи
1
2
3
4
5
xi1
2
4
8
12
13
xi2
10
7
6
11
9
17

18. Иерархические процедуры классификации

x2
12
4
1
10
5
8
2
3
6
4
2
0
0
2
4
6
8
10
12
14
x1
18

19. Иерархические процедуры классификации

РЕШЕНИЕ
1.1. Евклидова метрика. Принцип «ближнего соседа».
1, 2
k
2
2
2
(
x
x
)
(
2
4
)
(
10
7
)
3,61
1l 2l
l 1
1,3
k
2
2
2
(
x
x
)
(
2
8
)
(
10
6
)
7,21
1
l
3
l
l 1
1,1 0
19

20. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
0
3,61
R1 7,21
10,05
11,05
3,61 7,21 10,05 11,05
0
4,12 8,94 9,22
4,12
0
6,40 5,83
8,94 6,40
0
2,24
9,22 5,83 2,24
0
4,5
Имеем: S1, S2, S3, S4,5
20

21. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1 и S4,5 равно:
min ( S1 , S 4,5 )
1
1
1
1, 4 1,5 1, 4 1,5
2
2
2
1
1
(10,05 11,05) 10,05 11,05 10,05
2
2
21

22. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1, 2
3,61 7,21 10,05
0
0
4,12 8,94
3,61
R 2 7,21 4,12
0
5,83
0
10,05 8,94 5,83
1,( 4,5)
2 ,( 4 , 5 )
Имеем: S1,2, S3, S4,5
22

23. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1,2 и S4,5 равно:
1
1
1
min ( S 4,5 , S1, 2 ) ( 4,5),1 ( 4,5), 2 ( 4,5),1 ( 4,5), 2
2
2
2
1
1
(10,05 8,94) 10,05 8,94 8,94
2
2
23

24. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
(1, 2),3
4,12 8,94
0
R3 4,12
0
5,83
8,94 5,83 0
Имеем: S1,2,3, S4,5
0 5,83
R4
5,83 0
24

25. Иерархические процедуры классификации

Tree Diagram for 5 Cases
Single Linkage
Euclidean distances
C_1
C_2
C_3
C_4
C_5
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
Linkage Distance
25

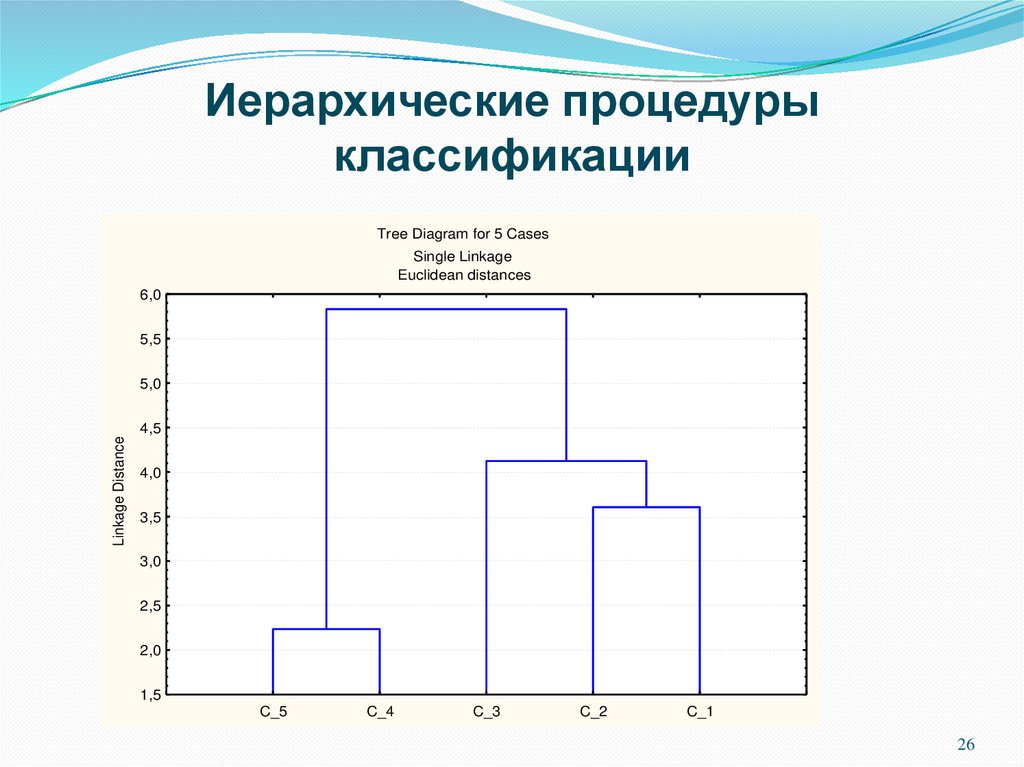
26. Иерархические процедуры классификации

Tree Diagram for 5 Cases
Single Linkage
Euclidean distances
6,0
5,5
5,0
Linkage Distance
4,5
4,0
3,5
3,0
2,5
2,0
1,5
C_5
C_4
C_3
C_2
C_1
26

27. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1.2. Принцип «дальнего соседа».
0
3,61
R1 7,21
10,05
11,05
3,61 7,21 10,05 11,05
0
4,12 8,94 9,22
4,12
0
6,40 5,83
8,94 6,40
0
2,24
9,22 5,83 2,24
0
4,5
Имеем: S1, S2, S3, S4,5
27

28. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1 и S4,5 равно:
max ( S1 , S 4,5 )
1
1
1
1, 4 1,5 1, 4 1,5
2
2
2
1
1
(10,05 11,05) 10,05 11,05 11,05
2
2
28

29. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1, 2
3,61 7,21 11,05
0
0
4,12 9,22
3,61
R 2 7,21 4,12
0
6,40
0
11,05 9,22 6,40
1,( 4,5)
2 ,( 4 , 5 )
Имеем: S1,2, S3, S4,5
29

30. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1,2 и S4,5 равно:
max
1
1
1
( S 4,5 , S1, 2 ) ( 4,5),1 ( 4,5), 2 ( 4,5),1 ( 4,5), 2
2
2
2
1
1
(11,05 9,22) 11,05 9,22 11,05
2
2
30

31. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
7,21 11,05
0
R3 7,21
0
6,40
11,05 6,40
0
3, ( 4 , 5 )
Имеем: S1,2, S3,4,5
11,05
0
R4
0
11,05
31

32. Иерархические процедуры классификации

Tree Diagram for 5 Cases
Complete Linkage
Euclidean distances
C_1
C_2
C_3
C_4
C_5
0
2
4
6
8
10
12
Linkage Distance
32

33. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1.3. Принцип «центра тяжести».
0
3,61
R1 7,21
10,05
11,05
3,61 7,21 10,05 11,05
0
4,12 8,94 9,22
4,12
0
6,40 5,83
8,94 6,40
0
2,24
9,22 5,83 2,24
0
4,5
Имеем: S1, S2, S3, S4,5
33

34. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Кластер S4,5 характеризуется центром тяжести:
X 4,5
12,5
10
Расстояние между кластерами S1 и S4,5 равно:
( 4,5),1 (12,5 2) 2 (10 10) 2 10,5
34

35. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1, 2
3,61 7,21 10,05
0
0
4,12 9,01
3,61
R 2 7,21 4,12
0
6,02
0
10,05 9,01 6,02
Имеем: S1,2, S3, S4,5
35

36. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Кластер S1,2 характеризуется центром тяжести:
3
X 1, 2
8,5
Расстояние между кластерами S1,2 и S4,5 равно:
( 4,5),(1, 2) (3 12,5) 2 (8,5 10) 2 9,62
36

37. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
3,(1, 2)
5,59 9,62
0
R3 5,59
0
6,02
9,62 6,02
0
Имеем: S1,2,3, S4,5
37

38. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Кластер S1,2,3 характеризуется центром тяжести:
(2 4 8) / 3 4,67
X 1, 2,3
(10 7 6) / 3 7,67
Расстояние между кластерами S1,2,3 и S4,5 равно:
(1, 2,3),( 4,5) (4,67 12,5) 2 (7,67 10) 2 8,17
0 8,17
R4
8,17 0
38

39. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1.4. Принцип «средней связи».
0
3,61
R1 7,21
10,05
11,05
3,61 7,21 10,05 11,05
0
4,12 8,94 9,22
4,12
0
6,40 5,83
8,94 6,40
0
2,24
9,22 5,83 2,24
0
4,5
Имеем: S1, S2, S3, S4,5
39

40. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1 и S4,5 равно:
1
1
( S1 , S 4,5 ) ( 1, 4 1,5 ) (10,05 11,05) 10,55
2
2
40

41. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
1, 2
3,61 7,21 10,55
0
0 8,94 9,08
3,61
R 2 7,21 8,94
0
6,12
0
10,55 9,08 6,12
Имеем: S1,2, S3, S4,5
41

42. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1,2 и S4,5 равно:
1
( S1, 2 , S 4,5 ) ( 1, 4 1,5 2, 4 2,5 ) 9,82
4
42

43. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
3,(1, 2)
0 5,41 9,82
R3 5,41 0 6,12
9,82 6,12 0
Имеем: S1,2,3, S4,5
43

44. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
Расстояние между кластерами S1,2,3 и S4,5 равно:
1
( S1, 2,3 , S 4,5 ) ( 1, 4 1,5 2, 4 2,5 3, 4 3,5 ) 8,58
6
0 8,58
R4
8,58 0
44

45. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
2.1. Взвешенное евклидово расстояние.
Принцип «ближнего соседа».
w1=0,05 и w2 = 0,95.
ВЕ ( X i , X j )
k
2
w
(
x
x
)
l il jl
l 1
1, 2 (2 4) 2 * 0,05 (10 7) 2 * 0,95 2,96
45

46. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
0
2,96
R1 4,12
2,44
2,65
2,3
2,96 4,12 2,44 2,65
0
1,32 4,29 2,80
1,32
0
4,95 3,13
4,29 4,95
0
1,96
2,80 3,13 1,96
0
Имеем: S1, S2,3,S4, S5
46

47. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
2,96 2,44 2,65
0
0
4,29 2,80
2,96
R 2 2,44 4,29
0
1,96
0
2,65 2,80 1,96
4,5
Имеем: S1, S2,3, S4,5
47

48. Иерархические процедуры классификации

РЕШЕНИЕ (продолжение)
2,96 2,44
0
R3 2,96
0
2,80
2,44 2,80
0
1,( 4,5)
Имеем: S1,,4,5, S2,3
2,80
0
R4
0
2,80
48

49.

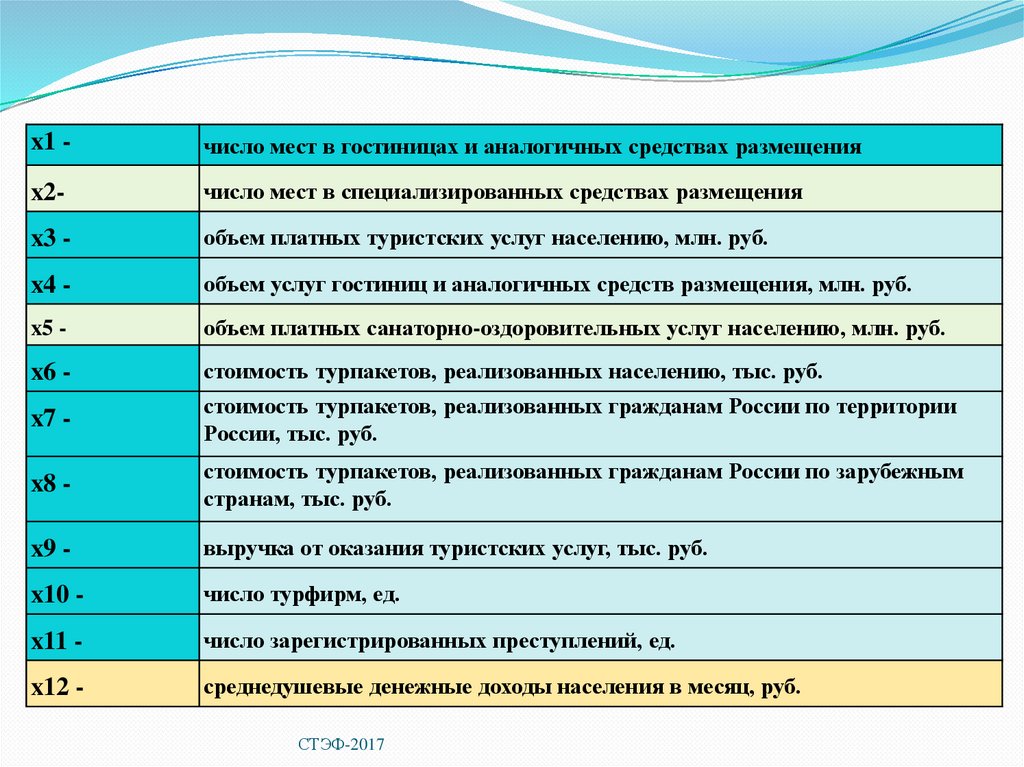
x1 -
число мест в гостиницах и аналогичных средствах размещения
x2-
число мест в специализированных средствах размещения
x3 -
объем платных туристских услуг населению, млн. руб.
x4 -
объем услуг гостиниц и аналогичных средств размещения, млн. руб.
x5 -
объем платных санаторно-оздоровительных услуг населению, млн. руб.
x6 -
стоимость турпакетов, реализованных населению, тыс. руб.
x7 -
стоимость турпакетов, реализованных гражданам России по территории
России, тыс. руб.
x8 -
стоимость турпакетов, реализованных гражданам России по зарубежным
странам, тыс. руб.
x9 -
выручка от оказания туристских услуг, тыс. руб.
x10 -
число турфирм, ед.
x11 -
число зарегистрированных преступлений, ед.
x12 -
среднедушевые денежные доходы населения в месяц, руб.
СТЭФ-2017

50. Метод K-средних

Метод
50

51. Метод K-средних

Метод
К-средних
многомерных
предназначен
наблюдений
на
для
разбиения
заданное
число
К кластеров, однородных в смысле геометрической
взаимной близости элементов, принадлежащих к одному
классу.
51

52. Метод K-средних

Метод К-средних обычно используется при достаточно
больших объемах n классифицируемых данных и
реализуется по следующей схеме.
На 1-м этапе производится последовательное
(итерационное) уточнение местоположения центров
(v )
тяжести
классов x
(v
–
номер
итерации).
При этом нулевое приближение
помощью
случайно
x
выбранных
исследуемой совокупности, т.е. x
(0)
строится с
первых
( 0)
(i )
К
точек
xi
52

53. Метод K-средних

Затем на j-й итерации «извлекается» точка xk j и
выясняется, к какому из эталонов x
(0)
(i )
она оказалась
ближе всего. Именно этот, самый близкий к xk j эталон
заменяется новым, определяемым как центр тяжести
старого эталона и присоединенной к нему точки xk j .
53

54. Метод K-средних

Имеем нулевое приближение:
x
( 0)
(i )
xi
w( 0) (i ) 1 , i = 1, 2, …, k
После «извлечения» новой точки xk+ν пересчет центров
тяжести и весов новых эталонов осуществляется по
следующим формулам:
54

55. Метод K-средних

w i 1 xi 1 xk
1
1
, если ( xk , xi ) min ( xk , x j )
(v)
1
1 j k
xi wi 1
xi 1
в противном случае
wi
(v)
w i 1 1, если ( xk , xi 1 ) min ( xk , x j 1 )
1 j k
w i 1
в противном случае
55

56. Метод K-средних

2-й этап метода K-средних посвящен соответственно
процедуре классификации.
Окончательное разбиение S исследуемой совокупности
на K классов производится в соответствии с правилом
«минимального
дистанционного
разбиения»
относительно центров тяжести:
наблюдение xi относится к классу j0 , если
( xi , x ( j ) ) min ( xi , x ( j ) )
0
1 j k
56

57. 58. Метод K-средних

59.

СТЭФ-2017

English Русский Rules