Принцип разделения источника и канала. Проверка формулы Шеннона

1. Принцип разделения источника и канала

Роль кодирования канала:
Борьба с ошибками в канале для надежной передачи данных
Роль кодирования источника(сжатие данных):
Облегчение хранения и передачи путем устранения
избыточности источника
1

2. Дискретный источник

Дискретный источник характеризуется с помощью
случайной переменной X, при этом задается алфавит
A(возможные исходы) и вероятностное распределение
P символов алфавита
Примеры
Бросание монеты: P(X=О)=P(X=Р)=1/2
Бросание кубика: P(X=k)=1/6, k=1,2,3,4,5,6
Раздача карт: P(X=П)=P(X=Ч)=P(X=Т)=P(X=Б)=1/4
2

3. Вычисление неопределенности события

h(p) p
log2ph(p)p
Вычисление неопределенности события
Информация простого события
- вероятность события x
примечания
1
0
0
должно произойти
(нет неопределнности)
навряд ли произойдет
(бесконечное количество неопределенности)
h(p)- разумная мера количества информации
3

4. Взвешенная информация простого события

p
h(p)hw(p) p h(p)
hw(p) p log2p
Взвешенная информация простого события
0
1/2
1
0
1
0
1/2
0
При возрастании p от 0 до 1, взвешенная информация
Сначала возрастает, а затем убывает
4

5.

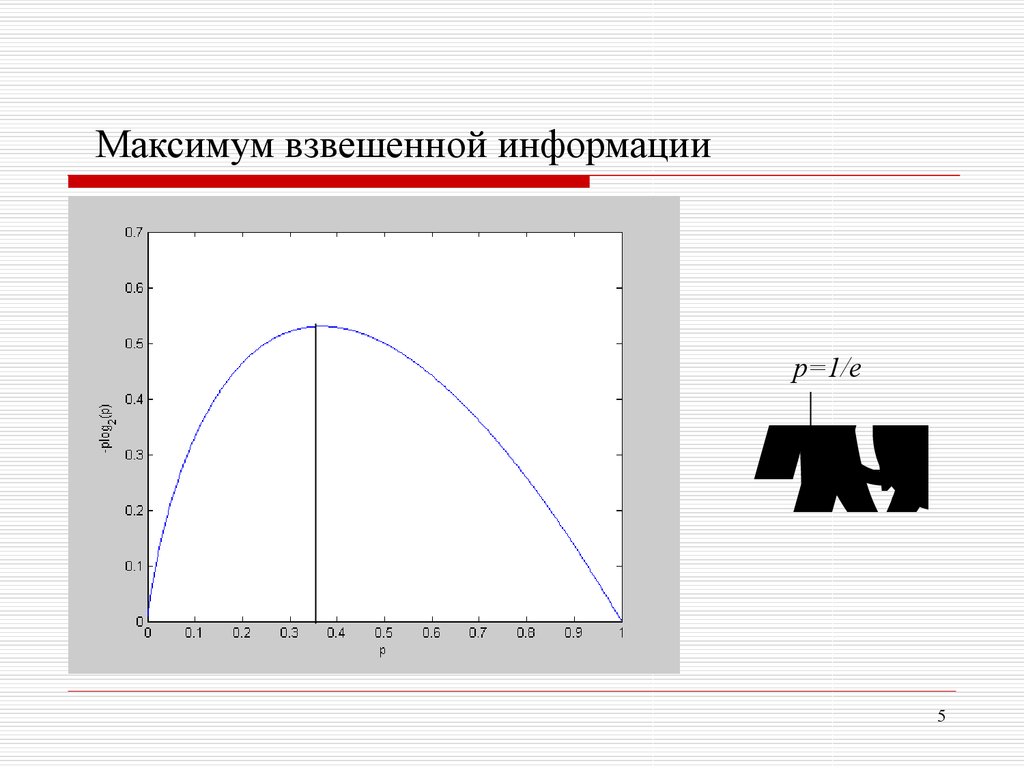
Максимум взвешенной информации
1
hw(p) eln2
p=1/e
5

6. Формула Шеннона для энтропии источника

(H
)(X
H
X
h
(
p
)
) plogp
N
w
i
iiN
1
i 12i
Формула Шеннона для энтропии
источника
(бит)
H(X) – разумная мера ожидаемого количества информации
6

7.

pH
X
()x О
)(p,logq2 1 qplo g2(qx) Р
)
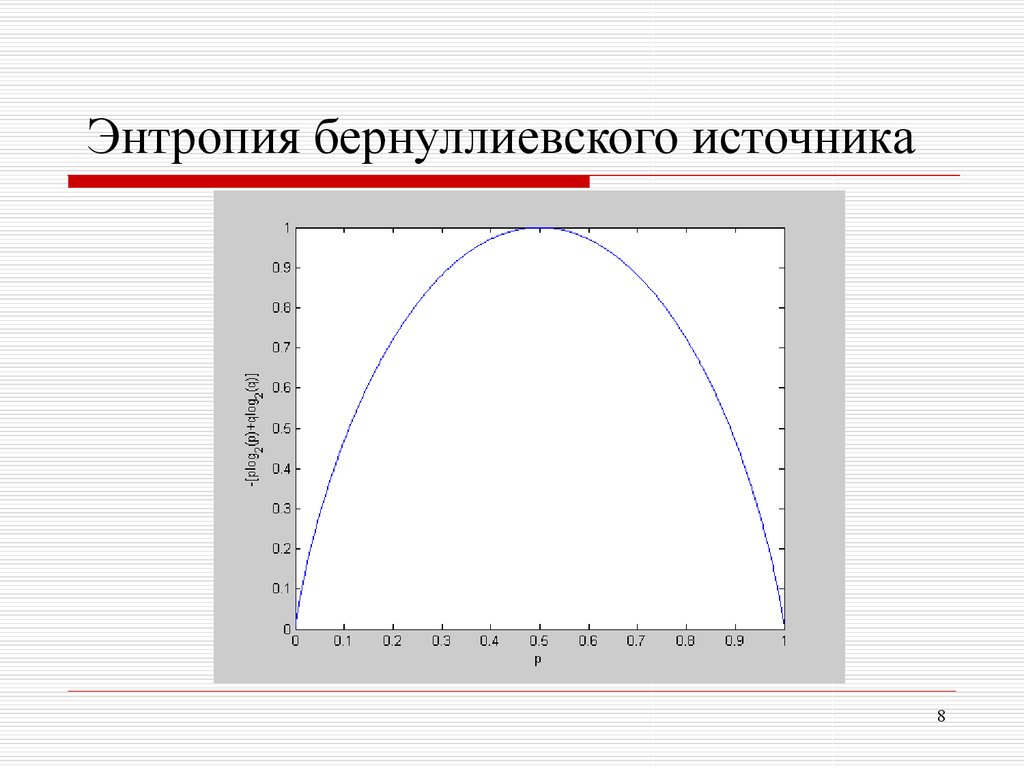
Пример (бернуллиевский источник)
Бросание монеты с вероятностью выпадания орла p (0<p<1)
Крайние случаи:
При p стремящемся к нулю, H(X) стремится к 0 бит наибольшее сжатие
При p стремящемся к половине, H(X) стремится к 1 бит никакое сжатие не
поможет
7

8.

Энтропия бернуллиевского источника
8

9. Некоторые свойства H(X)

Неотрицательная
Максимум достигается при равномерном
распределении
9

10. Какая польза от H(X)?

Первая теорема Шеннона (Шеннона-Хартли)
Для дискретного источника без памяти X, его
энтропия H(X) определяет минимальную среднюю
длину кода, необходимую для кодирования
источника
Грубая оценка: результаты N исходов источника могут
быть сжаты до NH(X) бит
10

11.

r l H
(X
) 0
Избыточность кода источника
Практическое значение
Теоретическая граница
11

12.

Проверка формулы Шеннона.
Игра в числа
{0,1,2,3,...,62,63}
12

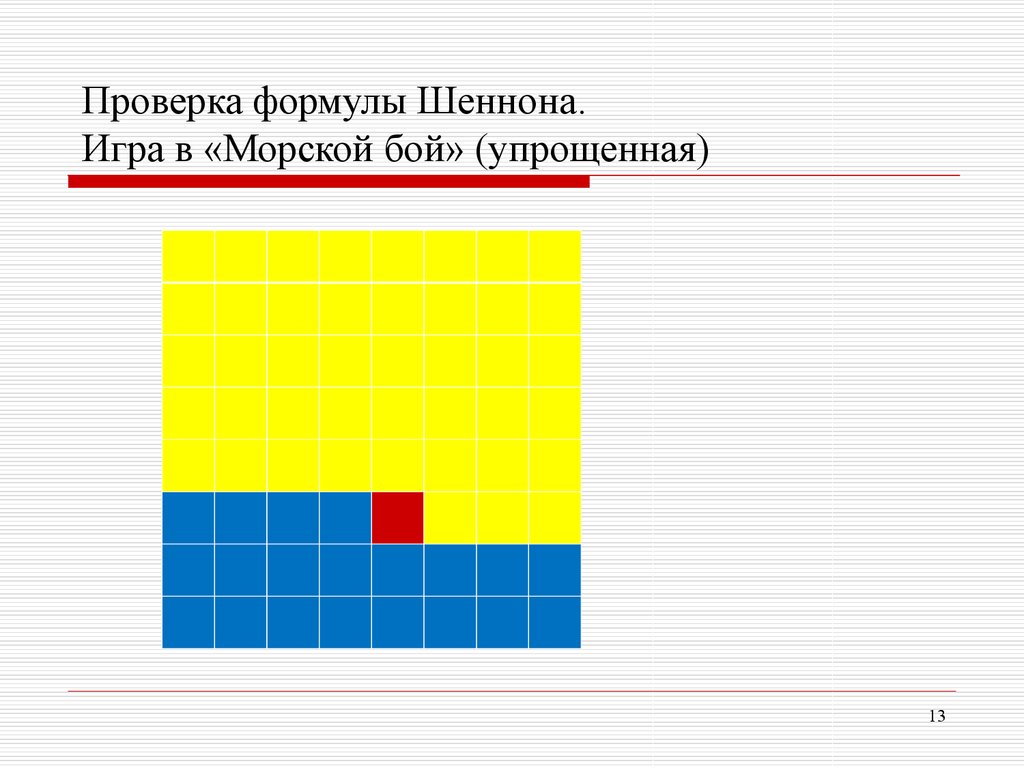
13.

Проверка формулы Шеннона.
Игра в «Морской бой» (упрощенная)
13

14.

Лотерея с «неправильной» монетой
Выигрышный номер определяется
подбрасыванием N=1000 раз
«неправильной» монеты: p(x=орел)=0,1;
p(x=решка)=0,9
Выигрыш – 100 000 000 000руб.
Номера билетов:
0000…………….00
0000…………….01
0000…………….10
…………………….
1111…………….11
Стоимость билетов –
100 руб.
Вопрос 1. Если Вам нужно выбрать только один билет,
который из номеров Вы выберете?
Вопрос 2. Чтобы гарантировать 99% успеха, сколько
билетов надо купить и какие из билетов?
14

15. Литература для чтения

М.Вернер. Основы кодирования.
Глава 2, Глава 3.
15