Программа Excel при работе с формулами

1. Введение

Целью курсовой работы является более
глубокое изучение программы Excel при
работе с формулами.
Задачей работы – корреляционный и
регрессионный анализ средствами Excel.

2. Корреляционный и регрессионный анализ

• Корреляционный
анализ – это
группа
Корреляционный
и регрессионный
анализ
статистических методов, направленная на
выявление и математическое представление
структурных зависимостей между
выборками.
• Регрессионный анализ - статистический
метод исследования зависимости случайной
величины от переменных.

3. Корреляционной-регрессионной анализ

Корреляционной-регрессионной
Метод корреляционного анализа часто не
ограничивается
нахождением тесноты связи между
анализ
исследуемыми
величинами.
Иногда
он
дополняется составлением уравнений регрессии,
которые получают с помощью одноименного
анализа, и представляющих собой описание
корреляционной
зависимости
между
результирующим и факторным (факторными)
признаком
(признаками).
Этот
метод
в
совокупности с рассматриваемым анализом
составляет метод корреляционно-регрессионного
анализа.

4. РЕШЕНИЕ ЗАДАЧИ В ПАКЕТЕ EXCEL

Экспериментальные данные
i
1
2
3
xᵢ
2,21
2,17
1,96
yᵢ
90
98
60
РЕШЕНИЕ ЗАДАЧИ В ПАКЕТЕ EXCEL
n=
Tα=
4
2,19
113
5
3,67
145
6
3,6
200
7
5,27
300
8
4,29
234
9
4,2
200
10
2,56
137
11
3,5
169
12
3,25
179
15
2,16
Статистические показатели:
My
Dy
Gy
Vy
R
=
=
=
=
=
151,47
4256,6
65,242
43,07%
0,9421
СРЗНАЧ(B4:P4)
ДИСП(B4:P4)
СТАНДОТКЛОН(B4:P4)
B14/B12*100%
КОРРЕЛ(B4:P4;B3:P3)
Проверка значимости коэффициента корреляции: удовлетворяет
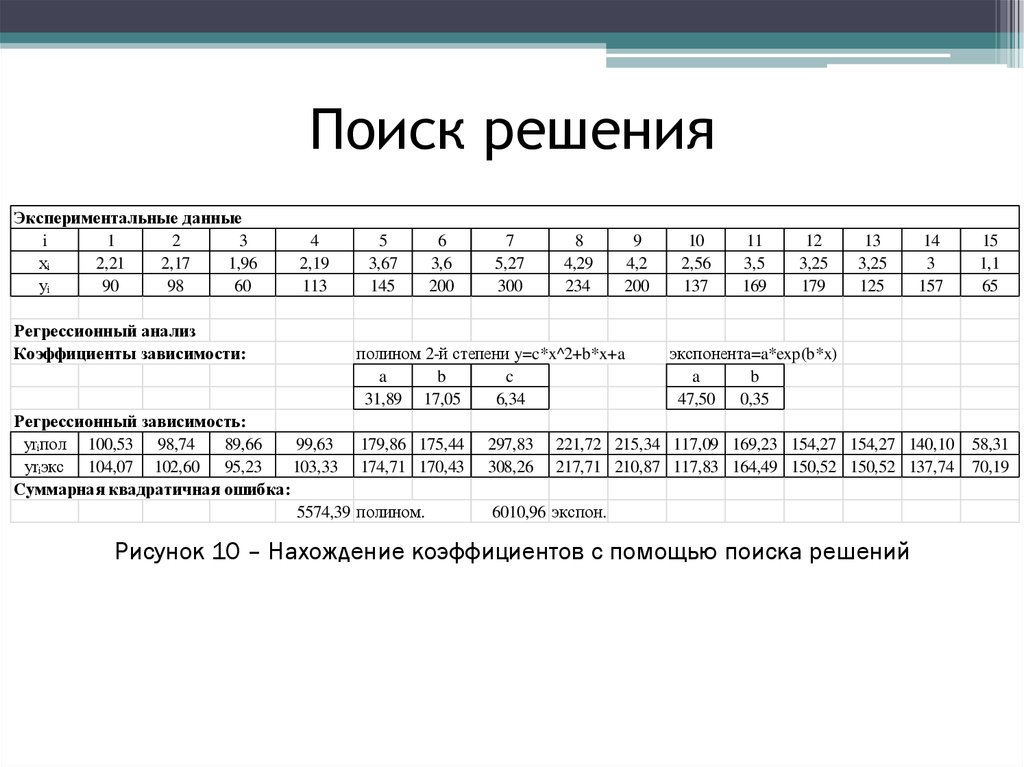
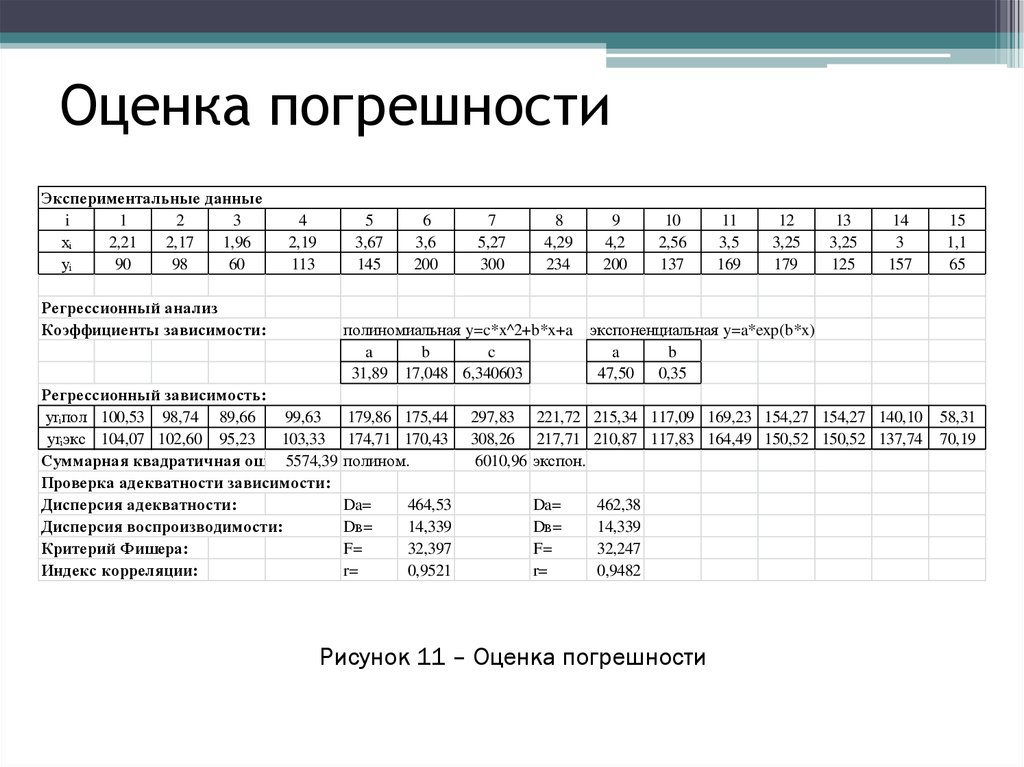
Рисунок 1 – Расчет статистических показателей в Excel
13
3,25
125
14
3
157
15
1,1
65

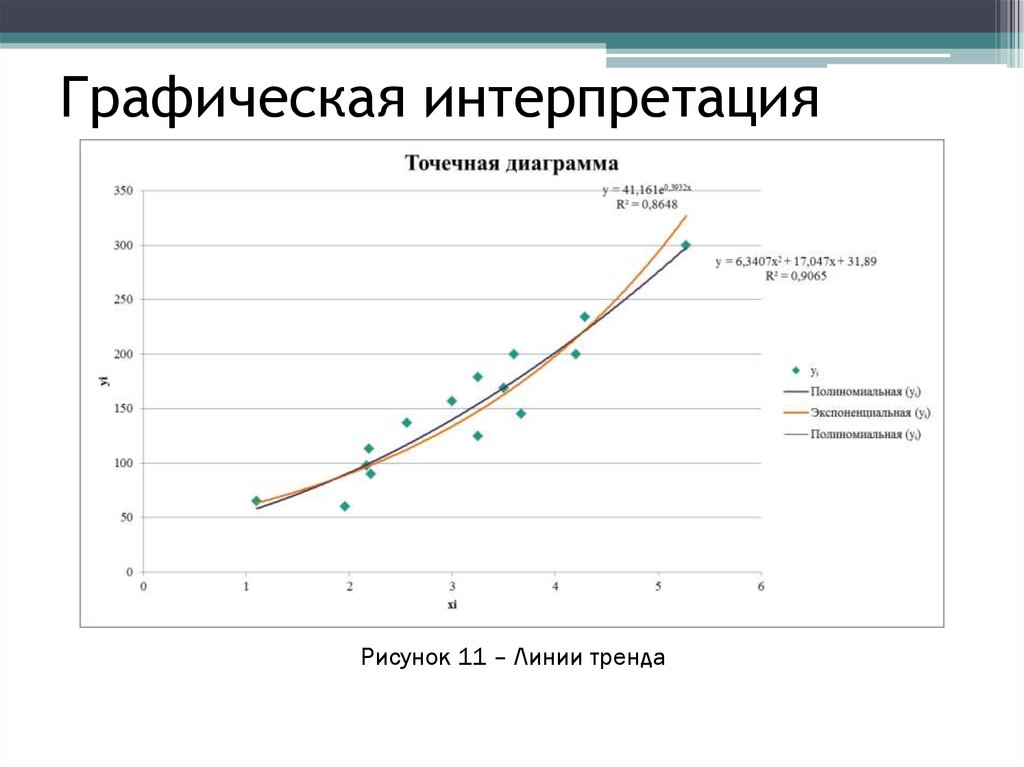
5. Полиномиальная функция 2-й степени

Система уравнений для определения параметров полинома 2-й степени

6. Полиномиальная функция 2-й степени

15,00
46,22
158,62
∆=
46,22
158,62
591,18
6783,82
158,62
591,18
2352,99
Рисунок 2 – Матрица коэффициентов
2272,00
7926,36
30055,66
∆1=
158,62
591,18
2352,99
-216336,49
46,22
158,62
591,18
15,00
46,22
158,62
∆2=
2272,00
7926,36
30055,66
115645,36
158,62
591,18
2352,99
15,00
46,22
158,62
∆3=
46,22
158,62
591,18
43013,94
2272,00
7926,36
30055,66
Рисунок 3 – Значения определитей

7. Полиномиальная функция 2-й степени

a0=Delta1\Delta=
a1=Delta2\Delta=
a2=Delta3\Delta=
31,89
17,05
6,34
Рисунок 4 – Коэффициенты по методу Крамера
a0=
a1=
a2=
31,89
17,05
6,34
Рисунок 5 – Коэффициенты по методу обратной матрицы

8. Экспоненциальная функция