Преобразование логических выражений

1.

Тема:
Преобразование
логических
выражений
Учитель информатики и ИКТ Бородина И.В.
МБОУ СОШ №13 ст. Новоджерелиевская
2011-2012 уч.год

2. Что нужно знать:

ЧТО НУЖНО ЗНАТЬ:
1). Условные обозначения логических операций:
¬ A,
не A (отрицание, инверсия)
A
A B,
A B
A и B (логическое умножение, конъюнкция)
A B, A B
A или B (логическое сложение, дизъюнкция)
A→B
импликация (следование)
A ↔ B,
A B
А В
исключающее или (только одно из А или В)
А
А В
эквиваленция (эквивалентность, равносильность)
В
А
В
А+В

3. Что нужно знать:

ЧТО НУЖНО ЗНАТЬ:
2). Таблицы истинности логических операций «И», «ИЛИ», «НЕ»,
«импликация», «эквиваленция», «исключающее ИЛИ»
А
В
А·В
А
В
А+В
А
A
0
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
1
1
А
В
А В
А
В
А В
А
В
А В
0
0
1
0
0
1
0
0
0
0
1
1
0
1
0
0
1
1
1
0
0
1
0
0
1
0
1
1
1
1
1
1
1
1
1
0

4. Что нужно знать:

ЧТО НУЖНО ЗНАТЬ:
3). Операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = ¬ A B или в других обозначениях A → B = A B
4). Операцию «эквиваленция» также можно выразить через «ИЛИ» и
«НЕ»:
A ↔ B = (¬ A ¬ B) (A B) или в других обозначениях A B = А B А В
5). Законы исключающее «ИЛИ»
А В = А В , А В = АВ АВ
6). Если в выражении нет скобок, сначала выполняются все операции «НЕ»,
затем – «И», затем – «ИЛИ», и самая последняя – «импликация».
7). Логическое произведение A∙B∙C∙… равно 1 (выражение истинно) только
тогда, когда все сомножители равны 1 (а в остальных случаях равно 0).
8). Логическая сумма A+B+C+… равна 0 (выражение ложно) только тогда,
когда все слагаемые равны 0 (а в остальных случаях равна 1)

5. Правила преобразования логических выражений (законы алгебры логики):

ПРАВИЛА ПРЕОБРАЗОВАНИЯ ЛОГИЧЕСКИХ
ВЫРАЖЕНИЙ (ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ):
Закон
Для И
двойного отрицания
исключения третьего
исключения
констант
Для ИЛИ
A A
A ·A 0
A A 1
A · 1 = A; A · 0 = 0
A + 0 = A; A + 1 = 1
повторения
A·A=A
A+A=A
поглощения
A · (A + B) = A
A+A· B =A
переместительный
A· B = B ·A
A+B=B+A
сочетательный
A · (B · C) = (A · B) · C
A + (B + C) = (A + B) + C
распределительный
A + B · C = (A + B) · (A + C)
A · (B + C) = A · B + A · C
де Моргана
A ·B A B
A B A ·B

6.

Сколько различных решений имеет система уравнений
(X2 X1) (X2 X3) (¬X2 ¬ X3)= 1
(X3 X1) (X3 X4) (¬X3 ¬ X4)= 1
...
(X9 X1) (X9 X10) (¬X9 ¬ X10)= 1
X10 X1 = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
( X 2 X1 ) X 2 X 3 X 2 X 3 1
( X 3 X1 ) X 3 X 4 X 3 X 4 1
...
( X 9 X1 ) X 9 X10 X 9 X10 1
X10 X1 0
2). Заметим, что по свойству
операции эквивалентности
X 2 X3 X 2 X3 ( X2 X3)
поэтому уравнения можно
переписать в виде
( X 2 X1 ) ( X 2 X 3 ) 1
( X 3 X1 ) ( X 3 X 4 ) 1
...
( X 9 X1 ) ( X 9 X 10 ) 1
X10 X1 0

7.

3). По таблице истинности находим варианты
( X 3 X1 ) ( X 3 X 4 ) 1
( X 2 X1 ) ( X 2 X 3 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
1
0
0
1
1
1
1
0
1
1
0
0
0
1
1
0
1
1
1
1
0
0
1
0
0
0
0
0
0
0
0
0
1
1
1
0
1
1
1
1
0
1
...

8.

4). Подключили Х4 – получили 8 решений, подключим X5 – получим
10 решений, X6 – получим 12 решений, X7 – получим 14 решений,
X8 – получим 16 решений, X9 – получим 18 решений, X10 – получим
20 решений.
5). Остается одно последнее уравнение X10 X1 = 0, из которого
следует, что X10 не равен X1, то есть из полученных 20 решений
нужно отбросить 2 решения, таким образом, получается 20 – 2 = 18
решений
Ответ: 18 решений

9.

Сколько различных решений имеет система уравнений
(X1 X2) (¬X1 ¬X2) (X1 X3) = 1
(X2 X3) (¬X2 ¬X3) (X2 X4) = 1
...
(X8 X9) (¬X8 ¬X9) (X8 X10) = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
X1 X 2 X1 X 2 ( X1 X 3 ) 1
X 2 X3 X 2 X3 ( X 2 X 4 ) 1
...
X 8 X 9 X 8 X 9 ( X 8 X10 ) 1
2). Заметим, что по свойству
операции эквивалентности
X1 X 2 X1 X 2 ( X1 X 2 )
поэтому уравнения можно
переписать в виде
( X1 X 2 ) ( X1 X 3 ) 1
(X2 X3) (X2 X4) 1
...
( X 8 X 9 ) ( X 8 X10 ) 1

10.

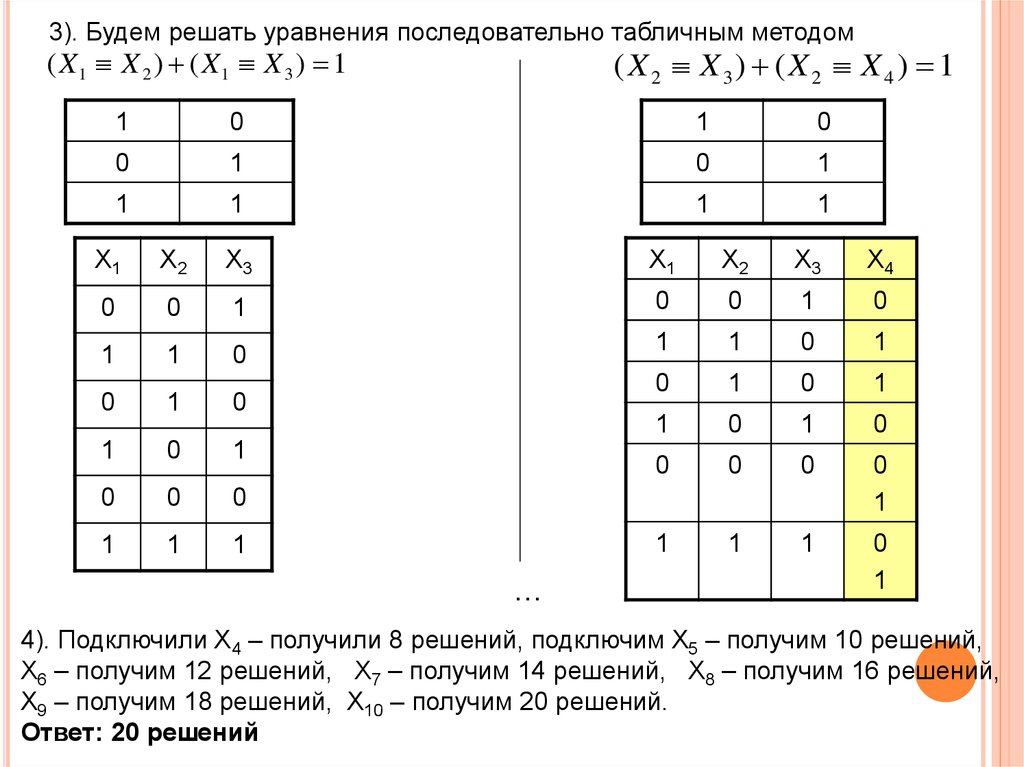
3). Будем решать уравнения последовательно табличным методом
(X2 X3) (X2 X4) 1
( X1 X 2 ) ( X1 X 3 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
1
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
0
0
1
1
1
...
4). Подключили Х4 – получили 8 решений, подключим X5 – получим 10 решений,
X6 – получим 12 решений, X7 – получим 14 решений, X8 – получим 16 решений,
X9 – получим 18 решений, X10 – получим 20 решений.
Ответ: 20 решений

11.

Сколько различных решений имеет система уравнений
(X1 X2) (X2 X10) (¬X2 ¬ X10)= 1
(X2 X3) (X3 X10) (¬X3 ¬ X10)= 1
...
(X8 X9) (X9 X10) (¬X9 ¬ X10)= 1
X10 X1 = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
2). Заметим, что по свойству
операции эквивалентности
X 2 X10 X 2 X10 ( X 2 X10 )
поэтому уравнения можно
переписать в виде
( X1 X 2 ) X 2 X10 X 2 X10 1
( X 1 X 2 ) ( X 2 X 10 ) 1
( X 2 X 3 ) X 3 X10 X 3 X10 1
( X 2 X 3 ) ( X 3 X 10 ) 1
...
( X 8 X 9 ) X 9 X10 X 9 X10 1
X 10 X 1 0
...
( X 8 X 9 ) ( X 9 X 10 ) 1
X10 X1 0

12.

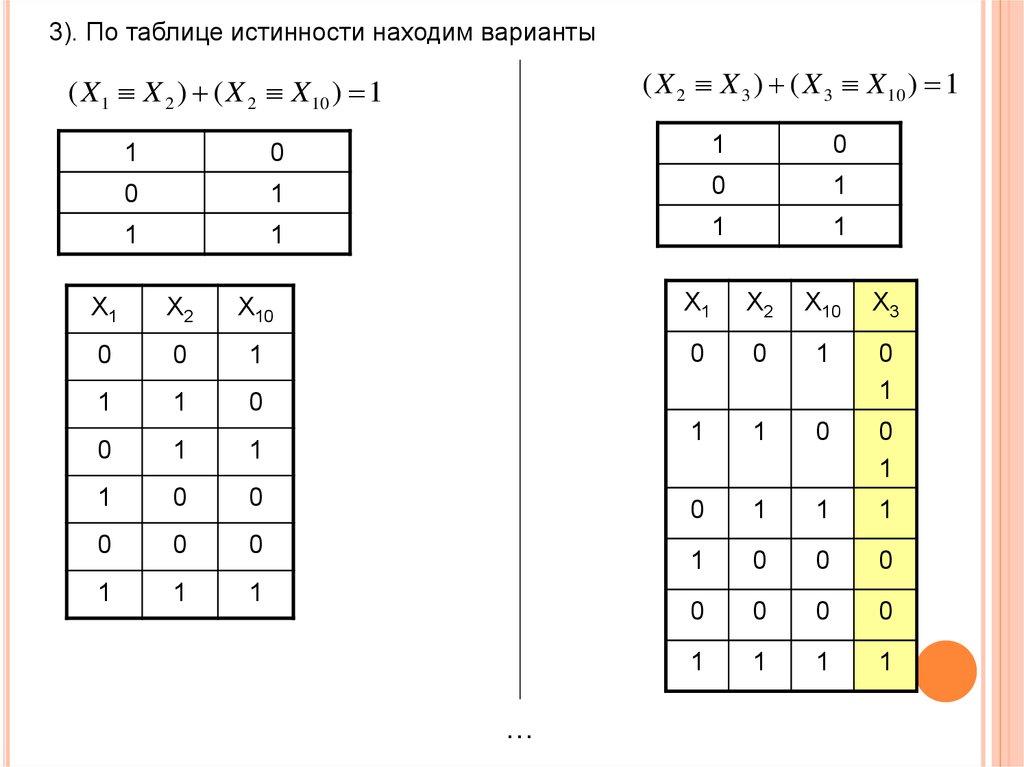
3). По таблице истинности находим варианты
( X 2 X 3 ) ( X 3 X 10 ) 1
( X 1 X 2 ) ( X 2 X 10 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х10
Х1
Х2
Х10
Х3
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
0
0
1
1
0
0
0
1
1
1
0
0
0
1
0
0
0
1
1
1
0
0
0
0
1
1
1
1
...

13.

4). Подключили Х3 – получили 8 решений, подключим X4 – получим 10
решений, X5 – получим 12 решений, X6 – получим 14 решений, X7 –
получим 16 решений, X8 – получим 18 решений, X9 – получим 20
решений.
5). Остается одно последнее уравнение X10 X1 = 0, из которого
следует, что X10 не равен X1, то есть из полученных 20 решений нужно
отбросить 2 решения, таким образом, получается 20 – 2 = 18 решений
Ответ: 18 решений

14.

Сколько различных решений имеет система уравнений
¬(X1 X2) (X1 X3) (¬X1 ¬X3)= 0
¬(X2 X3) (X2 X4) (¬X2 ¬X4)= 0
...
¬(X8 X9) (X8 X10) (¬X8 ¬X10)= 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
2). Заметим, что
( X1 X 3 ) ( X1 X 3 ) ( X1 X 3 ) ( Х 1 Х 3 ) ( Х1 Х 3 )
поэтому уравнения можно переписать в виде
( X1 X 2 ) ( X1 X 3 ) ( X1 X 3 ) 0
( X1 X 2 ) ( X1 X 3 ) 0
(X2 X3) (X2 X4 ) (X2 X4 ) 0
(X2 X3) (X2 X4 ) 0
...
( X 8 X 9 ) ( X 8 X10 ) ( X 8 X10 ) 0
...
( X 8 X 9 ) ( Х 8 Х10 ) 0

15.

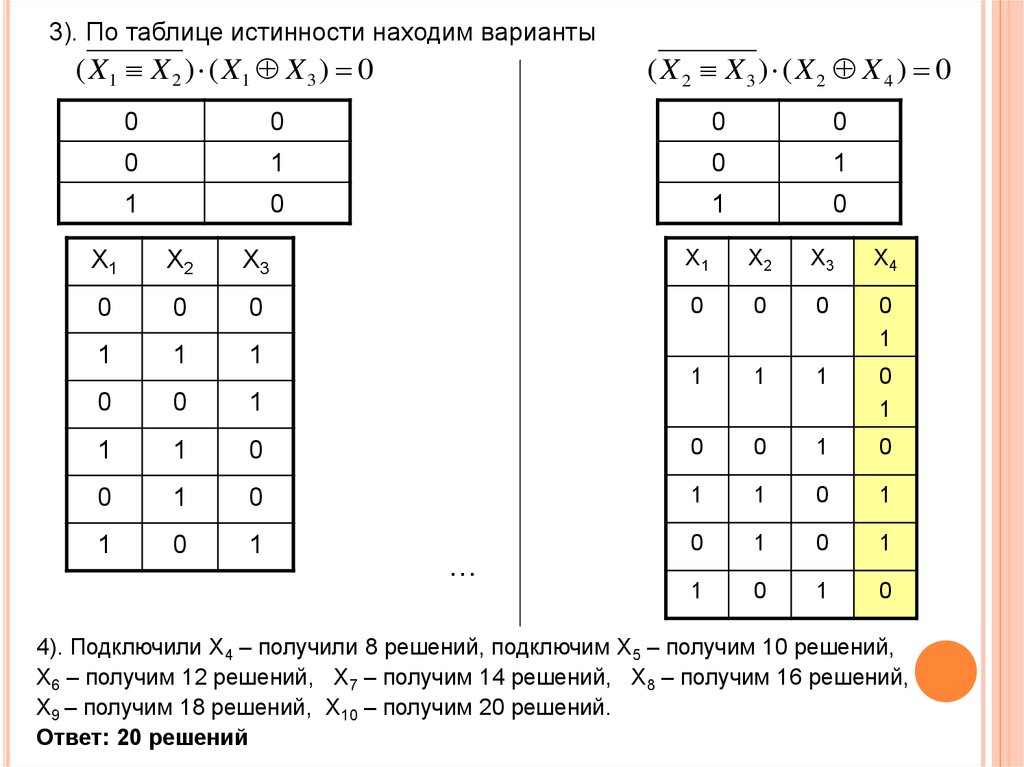
3). По таблице истинности находим варианты
( X1 X 2 ) ( X1 X 3 ) 0
(X2 X3) (X2 X4 ) 0
0
0
0
0
0
1
0
1
1
0
1
0
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
0
0
0
0
1
1
1
0
1
1
1
1
0
0
1
0
1
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
...
4). Подключили Х4 – получили 8 решений, подключим X5 – получим 10 решений,
X6 – получим 12 решений, X7 – получим 14 решений, X8 – получим 16 решений,
X9 – получим 18 решений, X10 – получим 20 решений.
Ответ: 20 решений

16.

Сколько различных решений имеет система уравнений
((X1 X2) (X3 X4)) (¬(X1 X2) ¬(X3 X4)) = 1
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 1
…
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
(( Х1 Х 2 ) ( X 3 X 4 )) (( X1 Х 2 ) ( Х 3 Х 4 )) 1
(( Х 3 Х 4 ) ( X 5 X 6 )) (( X 3 Х 4 ) ( X 5 Х 6 )) 1
...
(( Х 7 Х 8 ) ( X 9 X10 )) (( X 7 Х 8 ) ( X 9 Х10 )) 1
2). Раскроем скобки и перепишем
систему уравнений в виде
( Х1 Х 2 ) ( X 3 X 4 ) ( X1 Х 2 ) ( Х 3 Х 4 ) 1
(Х3 Х4 ) (X5 X6 ) (X3 Х4 ) (Х5 Х6 ) 1
...
( Х 7 Х 8 ) ( X 9 X10 ) ( X 7 Х 8 ) ( Х 9 Х10 ) 1
3). Используя закон исключающее
«ИЛИ», перепишем систему уравнений
в виде
( Х1 Х 2 ) ( X 3 X 4 ) 1
(Х3 Х4) (X5 X6) 1
...
( Х 7 Х 8 ) ( X 9 X 10 ) 1

17.

4). По таблице истинности находим варианты
( Х1 Х 2 ) ( X 3 X 4 ) 1
(Х3 Х4) (X5 X6) 1
0
1
0
1
1
0
1
0
Х1
Х2
Х3
Х4
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
1
1
0
4). Количество переменных:
X4 – получили 8 решений, X6 – получили
16 решений, X8 – получим 32 решения,
X10 – получим 64 решения.
Ответ: 64 решения
...
Х1
Х2
Х3
Х4
Х5
Х6
0
1
0
0
0
1
1
0
0
1
1
1
0
1
1
0
1
0
0
0
0
1
1
0
1
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
0
0
1
0
1
1
1
0
1
0
1
0
1
1
1
1
0
0
1
0
1

18.

Используемые
источники
Ссылка на используемый источник при
подготовке презентации:
http://kpolyakov.narod.ru/download/B15.doc