Find the acceleration centers of two identical disks moving down

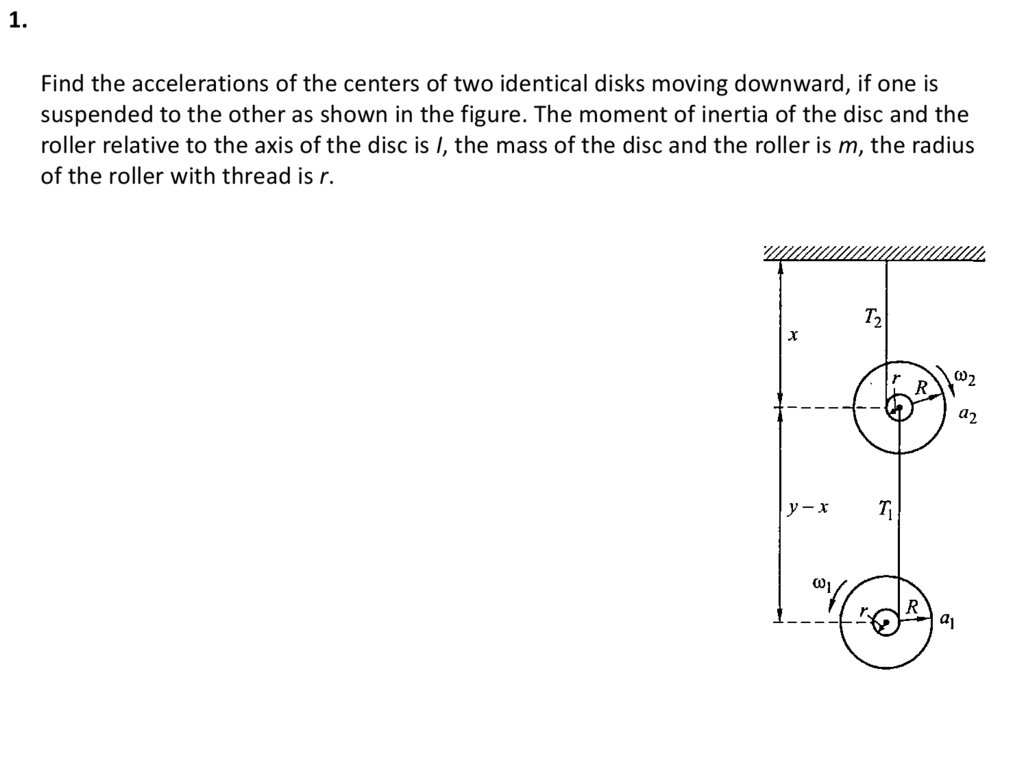
1.

1.
Find the accelerations of the centers of two identical disks moving downward, if one is
suspended to the other as shown in the figure. The moment of inertia of the disc and the
roller relative to the axis of the disc is I, the mass of the disc and the roller is m, the radius
of the roller with thread is r.

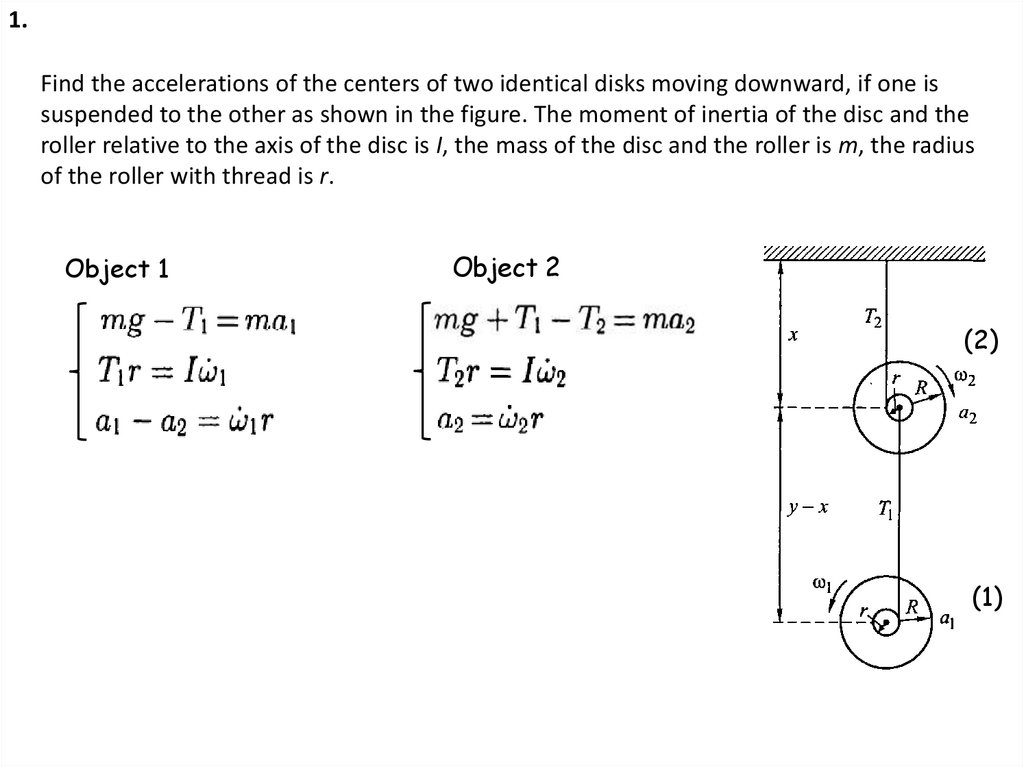
2.

1.
Find the accelerations of the centers of two identical disks moving downward, if one is
suspended to the other as shown in the figure. The moment of inertia of the disc and the
roller relative to the axis of the disc is I, the mass of the disc and the roller is m, the radius
of the roller with thread is r.
Object 1
Object 2
(2)
(1)

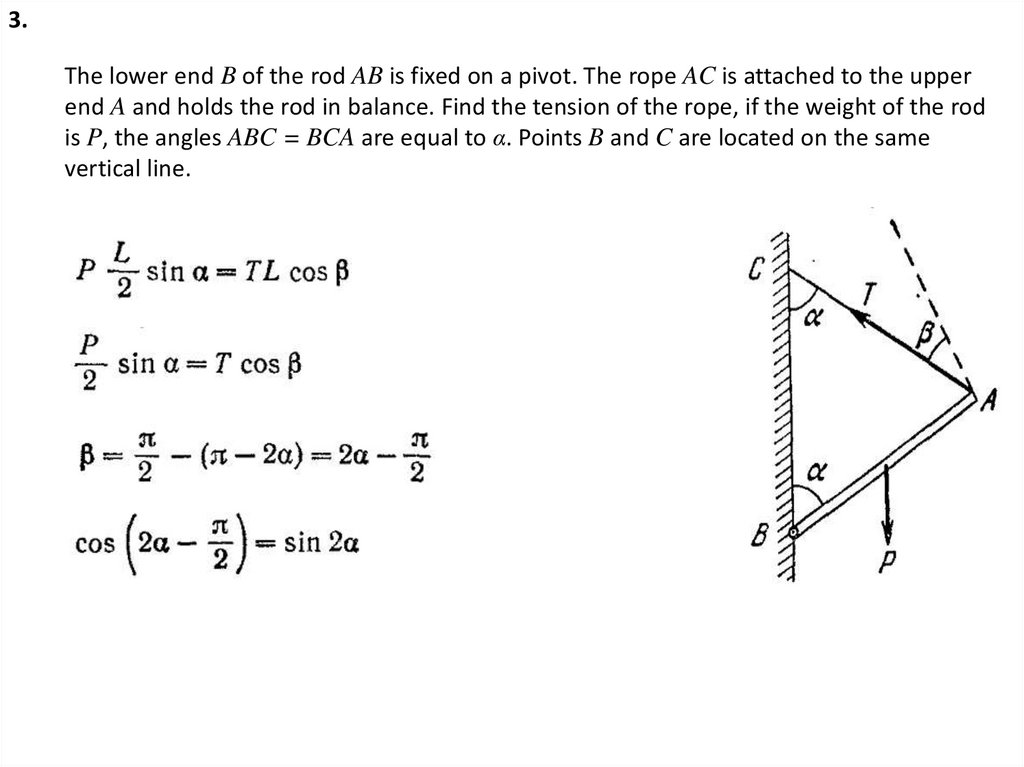
3.

1.
Find the accelerations of the centers of two identical disks moving downward, if one is
suspended to the other as shown in the figure. The moment of inertia of the disc and the
roller relative to the axis of the disc is I, the mass of the disc and the roller is m, the radius
of the roller with thread is r.
Object 1
Object 2
(2)
Answer
(1)

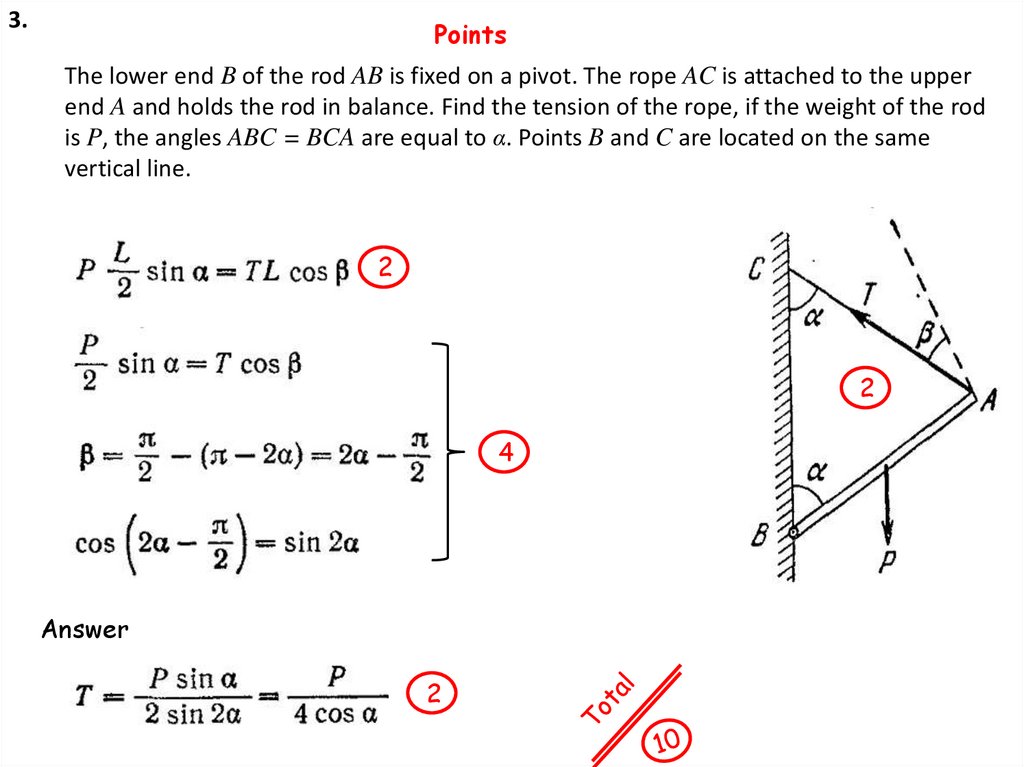
4.

1.
Points
Find the accelerations of the centers of two identical disks moving downward, if one is
suspended to the other as shown in the figure. The moment of inertia of the disc and the
roller relative to the axis of the disc is I, the mass of the disc and the roller is m, the radius
of the roller with thread is r.
Object 2
Object 1
1
1
1
1
1
(2)
1
Answer
2
2
(1)

5.

2.
The thin hoop rolls down without slipping on the surfaces of the inclined plane and
then the horizontal plane. What is the height the hoop will jump if its initial height is
h? The hoop and the plane are assumed to be perfectly elastic. The inclination angle
of the plane with respect to the horizon is α.

6.

2.
The thin hoop rolls down without slipping on the surfaces of the inclined plane and
then the horizontal plane. What is the height the hoop will jump if its initial height is
h? The hoop and the plane are assumed to be perfectly elastic. The inclination angle
of the plane with respect to the horizon is α.
Just before the jump
Just after the jump

7.

2.
The thin hoop rolls down without slipping on the surfaces of the inclined plane and
then the horizontal plane. What is the height the hoop will jump if its initial height is
h? The hoop and the plane are assumed to be perfectly elastic. The inclination angle
of the plane with respect to the horizon is α.
Just before the jump
Just after the jump
x
Answer

8.

2.
Points
The thin hoop rolls down without slipping on the surfaces of the inclined plane and
then the horizontal plane. What is the height the hoop will jump if its initial height is
h? The hoop and the plane are assumed to be perfectly elastic. The inclination angle
of the plane with respect to the horizon is α.
Just before the jump
2
1
Just after the jump
2
1
Answer
3

9.

3.
The lower end B of the rod AB is fixed on a pivot. The rope AC is attached to the upper
end A and holds the rod in balance. Find the tension of the rope, if the weight of the rod
is P, the angles ABC = BCA are equal to α. Points B and C are located on the same
vertical line.

10.

3.
The lower end B of the rod AB is fixed on a pivot. The rope AC is attached to the upper
end A and holds the rod in balance. Find the tension of the rope, if the weight of the rod
is P, the angles ABC = BCA are equal to α. Points B and C are located on the same
vertical line.

11.

3.
The lower end B of the rod AB is fixed on a pivot. The rope AC is attached to the upper
end A and holds the rod in balance. Find the tension of the rope, if the weight of the rod
is P, the angles ABC = BCA are equal to α. Points B and C are located on the same
vertical line.
Answer

12.

3.
Points
The lower end B of the rod AB is fixed on a pivot. The rope AC is attached to the upper
end A and holds the rod in balance. Find the tension of the rope, if the weight of the rod
is P, the angles ABC = BCA are equal to α. Points B and C are located on the same
vertical line.
2
2
4
Answer
2

13.

4.
A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a
mount B of mass m2. A constant horizontal force F is applied to the end K of a light thread
tightly wound on the cylinder. The friction between the mount and the supporting
horizontal plane is assumed to be absent. Find the acceleration of the point K.

14.

4.
A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a
mount B of mass m2. A constant horizontal force F is applied to the end K of a light thread
tightly wound on the cylinder. The friction between the mount and the supporting
horizontal plane is assumed to be absent. Find the acceleration of the point K.
Translational motion:
Rotational motion:
Acceleration of the point K:

15.

4.
A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a
mount B of mass m2. A constant horizontal force F is applied to the end K of a light thread
tightly wound on the cylinder. The friction between the mount and the supporting
horizontal plane is assumed to be absent. Find the acceleration of the point K.
Translational motion:
Rotational motion:
Acceleration of the point K:
Answer:

16.

Points
4.
A uniform solid cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a
mount B of mass m2. A constant horizontal force F is applied to the end K of a light thread
tightly wound on the cylinder. The friction between the mount and the supporting
horizontal plane is assumed to be absent. Find the acceleration of the point K.
Translational motion:
2
Rotational motion:
2
Acceleration of the point K:
Answer:
3
3