Similar presentations:
Системы счисления. Лекция 5
1.
Лекция 5СИСТЕМЫ СЧИСЛЕНИЯ
1. Кодирование и единицы измерения
информации. Представление числовой
информации в ПЭВМ.
2. Системы счисления, применяемые в
ПЭВМ.
3. Способы перевода чисел из одной
позиционной системы счисления в другую.
4. Формы представления чисел в ПЭВМ.
5. Способы кодирования двоичных чисел в
ПЭВМ.
2.
Виды информациипо ее форме представления
цифровая;
текстовая;
звуковая;
графическая;
видеоинформация
3.
Возможностьпредставления
информации
двоичными
цифрами
ВИЛЬГЕЛЬМ ЛЕЙБНИЦ
(1646-1716)
4.
Кол-во… 32
разрядов 1 2 3 4 8 16
(бит)
Число
32
1
2
3
4
2 2 2 2
2 =
8
16
возмож2=
2 =
= = = =
4294967
ных
256 65536
2 4 8 16
296
значений
0 или 1
00, 01, 10, 11
000, 001, 010, 011, 100, 101, 110, 111
m
N = 2 , где
N – количество независимых кодируемых
значений;
m – разрядность двоичного кодирования
5.
Единицы измерения информации:1 бит =1 двоичный разряд= 0 или 1.
1 байт=8 бит(byte), количество битов,
используемое для кодирования одного
символа.
1 Кбайт = 1024 байт = 210 байт.
1 Мбайт = 1024 Кбайт = 220 байт
1 Гбайт = 1024 Мбайт = 230 байт
1 Тбайт = 1024 Гбайт = 240 байт
6.
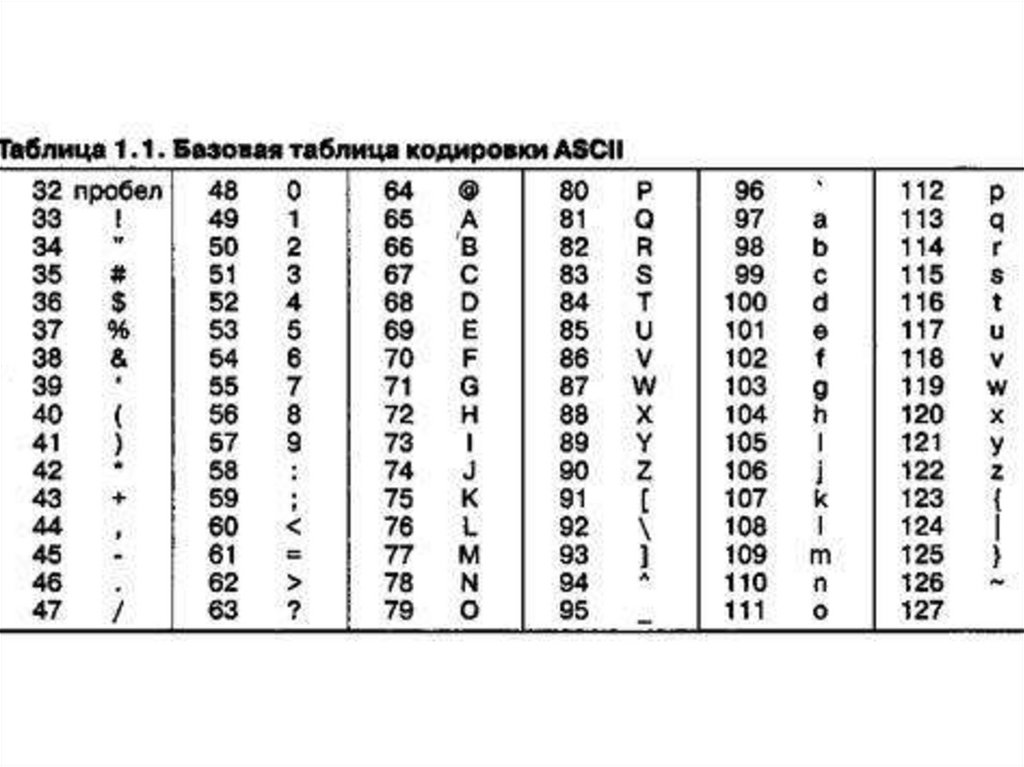
КОДИРОВАНИЕ ТЕКСТОВЫХ ДАННЫХASCII
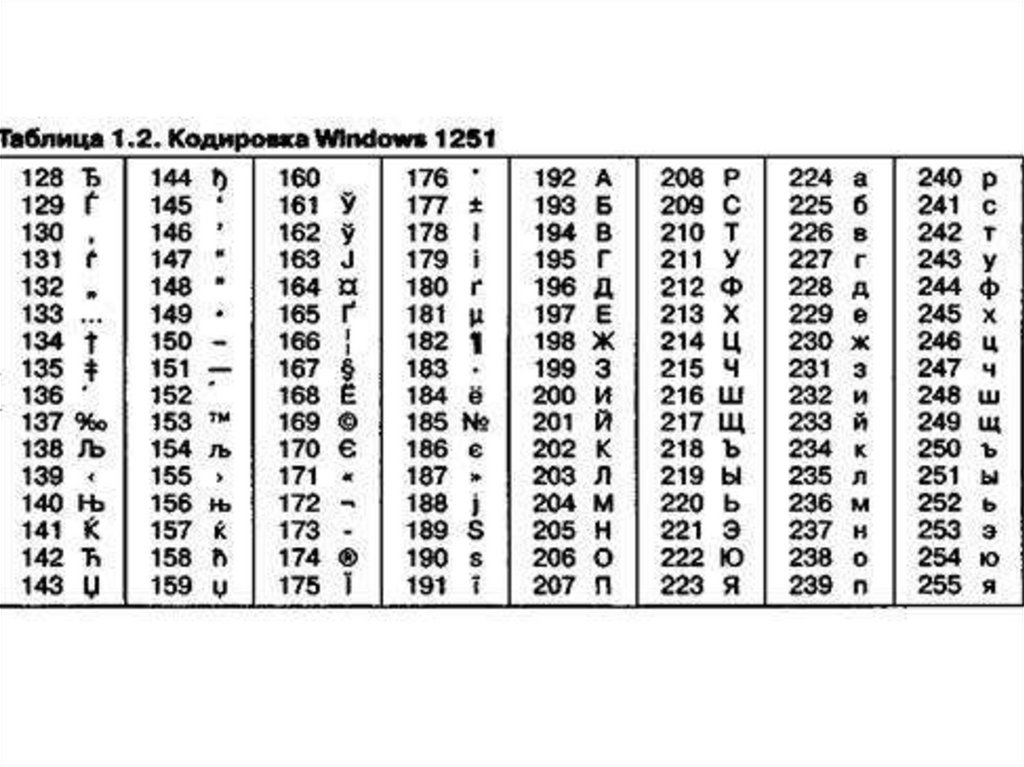
Windows-1251
КОИ-8
ISO
ГОСТ и ГОСТ-альтернативная
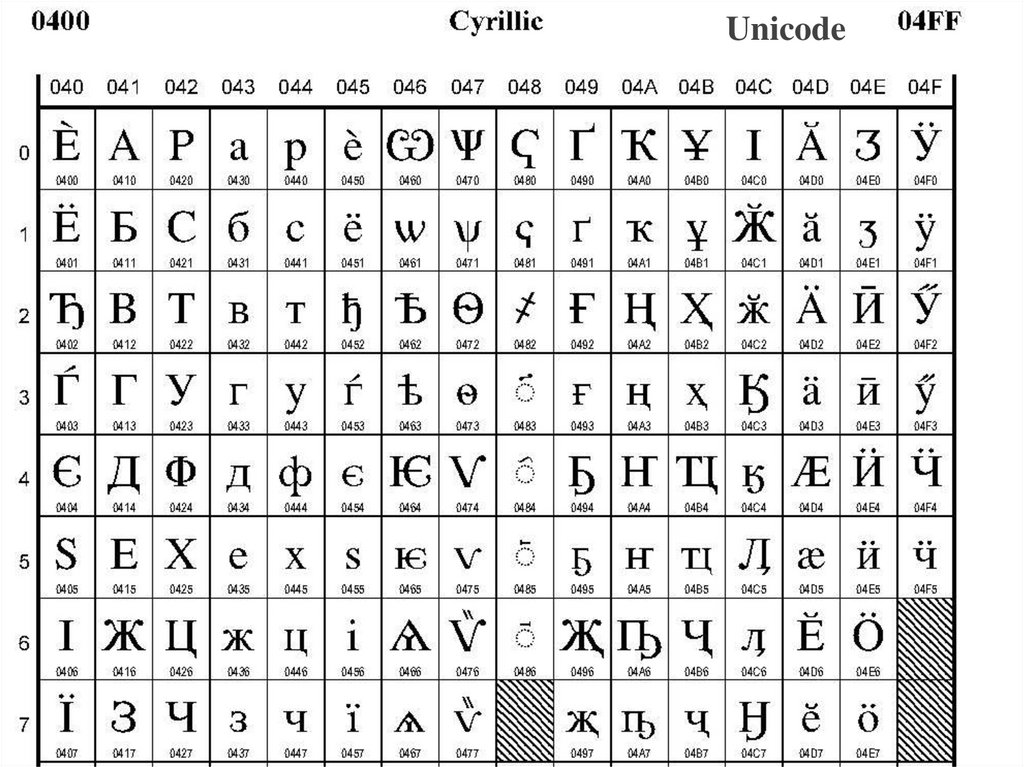
Unicode
7.
8.
9.
10.
Unicode11.
КОДИРОВАНИЕ ГРАФИЧЕСКИХ ДАННЫХпиксели (picture element)
номер(координаты) точки
код цвета(сумма RGB)
12.
КОДИРОВАНИЕ ЗВУКОВОЙ ИНФОРМАЦИИМетод FM (Frequency Modulation)
Метод таблично-волнового (WaveTable) синтеза
13.
СИСТЕМЫ СЧИСЛЕНИЯнепозиционные
позиционные
14.
НепозиционныеСистемы
счисления
Кирилли́ческая
15.
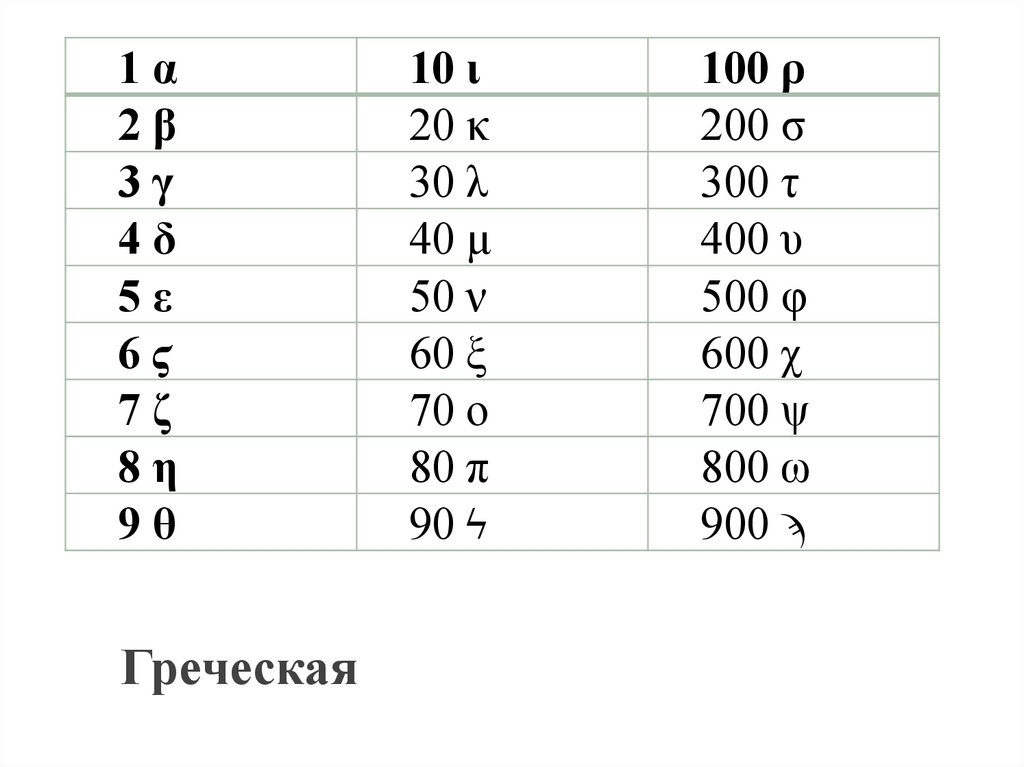
1α2β
3γ
4δ
5ε
6ϛ
7ζ
8η
9θ
Греческая
10 ι
20 κ
30 λ
40 μ
50 ν
60 ξ
70 ο
80 π
90 ϟ
100 ρ
200 σ
300 τ
400 υ
500 φ
600 χ
700 ψ
800 ω
900 ϡ
16.
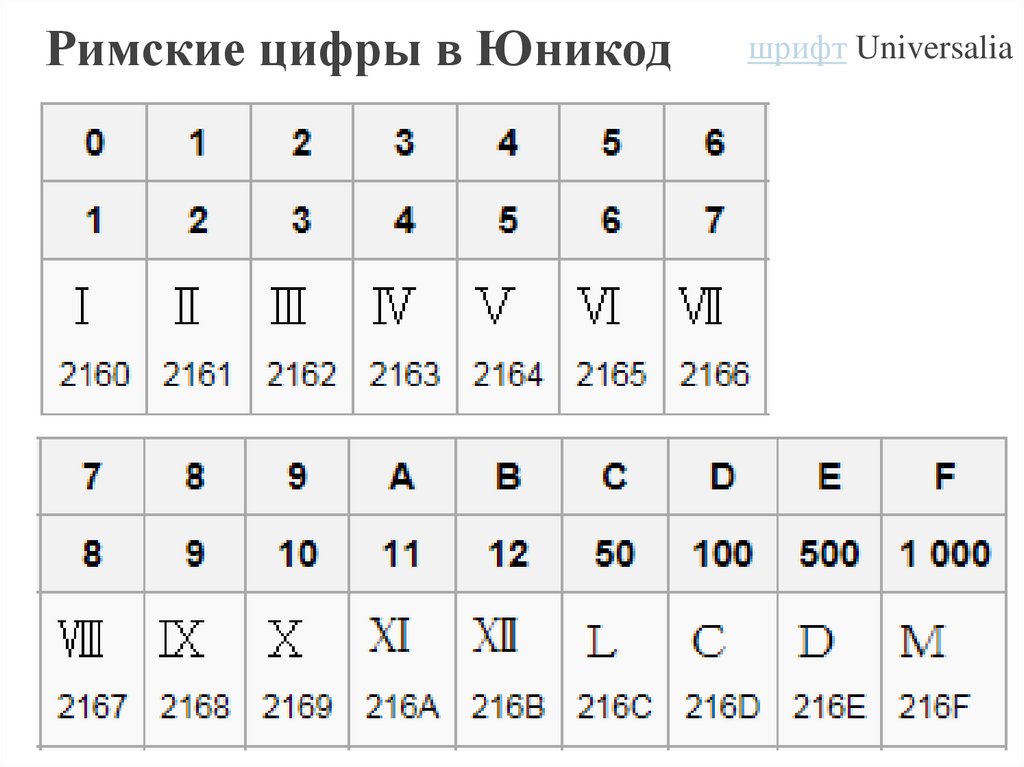
Римские цифры в Юникодшрифт Universalia
17.
18.
Позиционные системы счисленияоднородные
А10 = 131 = 100 + 30 + 1
смешанные
система измерения углов и дуг
система измерения времени
19.
307 известных системах счислениятолько лишь первобытных народов
американского континента
древнегреческий абак был основан на
двоично-пятиричной системе
счисления
Троичная система счисления (“Сетунь”)
20.
Основные характеристикипозиционных систем счисления :
основание системы счисления q;
значения цифр (символов) ak ;
вес разряда (позиции) в числе Rj,
где j – номер разряда.
Rj = qj
R0 = 100 = 1;
R2 = 102 = 100;
R1 = 101 = 10;
R-1= 10-1 = 0,1;
21.
1961,56 =1*103 + 9*102 + 6*101 + 1*100 +5*10-1 + 6*10-2
A a q
q
n 1
n 1
0
1
... a0 q a 1 q ... am q
m
n 1
a q
k m
k – номер разряда числа;
m – количество разрядов дробной
части числа;
n – количество разрядов в целой части
числа;
a k – значение цифры в k-м разряде.
k
k
22.
:...
...
a
a
a
a
a
Ak n 1 n 2 0 1 m
n 1
a
k m
k
23.
Двоичная система счисления (q = 210 = 102)A2
n 1
a
k m
10
,
где
0
,
1
.
ak
k
k
2
...
,
...
A2 an 1 a0 a 1 a m
110
,
01
A2
1
2
1 10 1 10 0 10 0 10 1 10
10
2
1
2
0
2
1
10
2
10
10
2
1 2 1 2 0 2 0 2 1 2 6,2510
2
10
1
10
0
10
24.
Шестнадцатеричная система счисления(q = 1610 = 1016)
0, 1, …, 9
1010= А16,
1110 = В16,
1210 = С16,
1310 = D16,
1410 = E16,
1510 = F16
E616
14 16 6 16 23010.
1
10
0
10
25.
16A
n 1
a
k m
k
10 ,
k
16
a k 0,1,2,3,4,5,6,7,8,9, A, B, C , D, E , F .
26.
Способы перевода чисел из однойпозиционной системы счисления в
другую
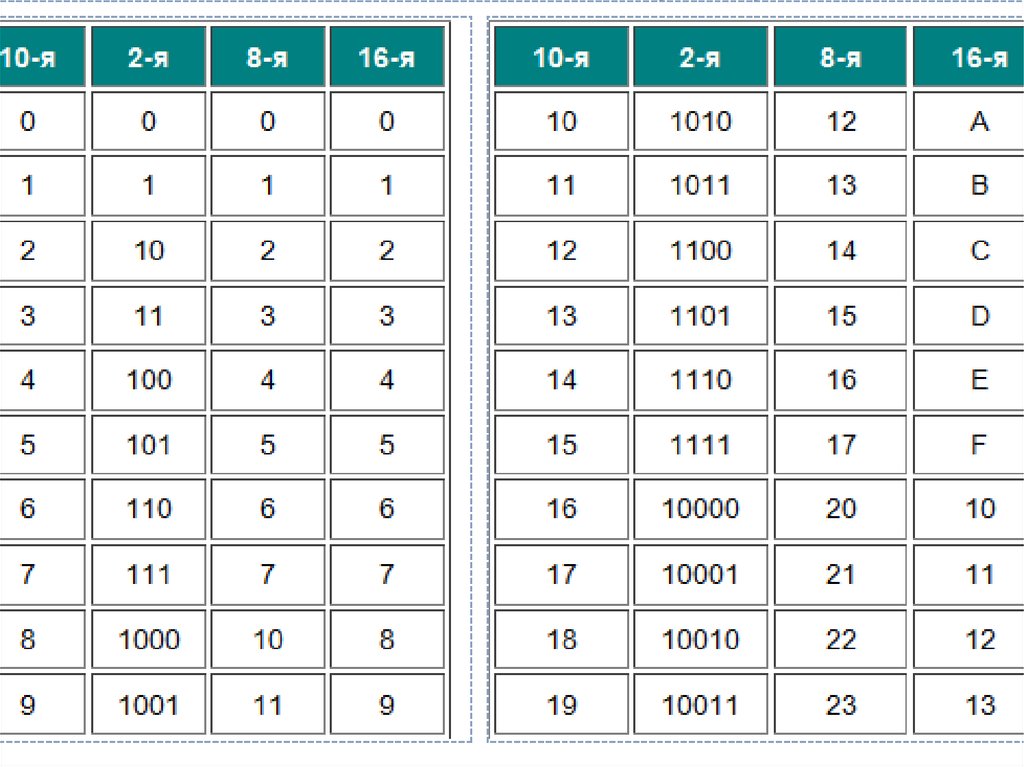
Табличный метод
27.
28.
29.
30.
31.
32.
Расчетный методперевод целых чисел,
перевод правильных дробей,
перевод неправильных
дробей
33.
перевод целых чисел(19)10 = (10011)2
34.
int dec, bin=0, j;// из десятичного в двоичное
cin >> dec;
for(j=0; dec>0; j++)
{
bin+=(dec%2)*powl(10,j);
dec/=2;
}
cout <<bin<< endl;
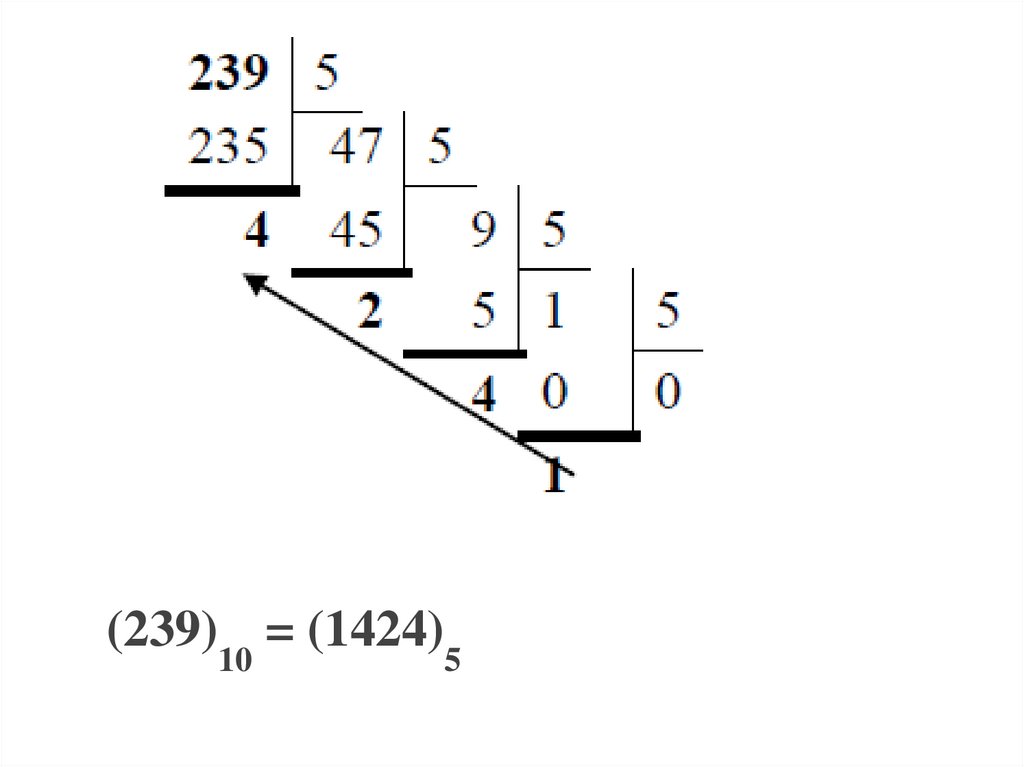
35.
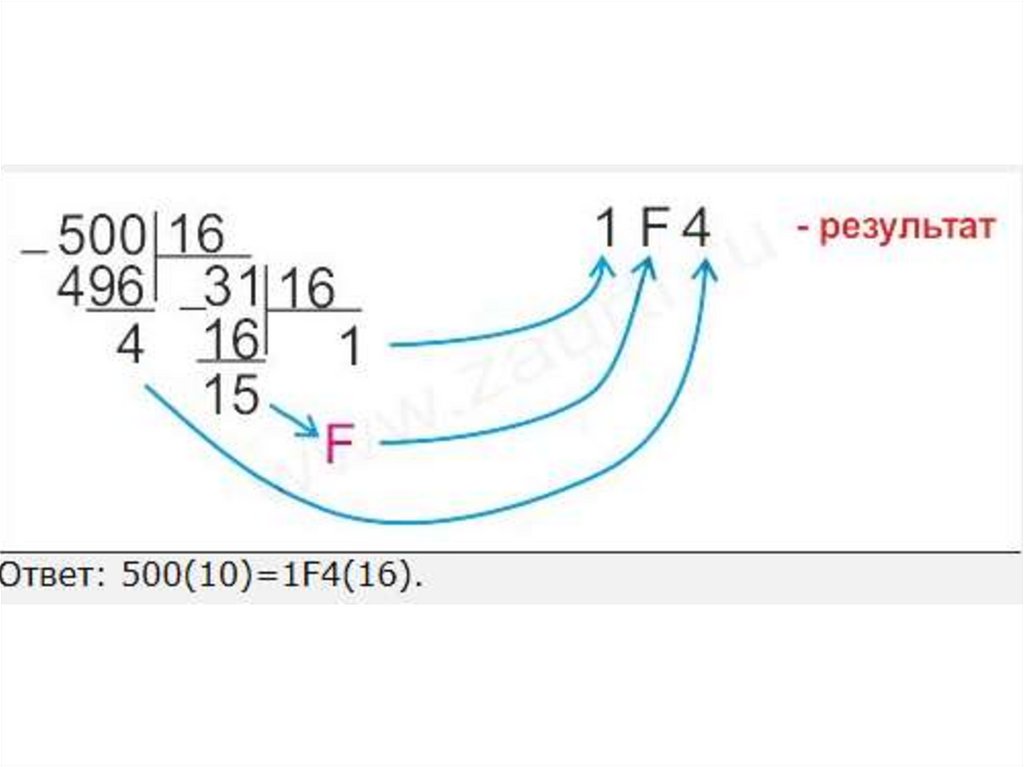
(239)10 = (1424)536.
37.
38.
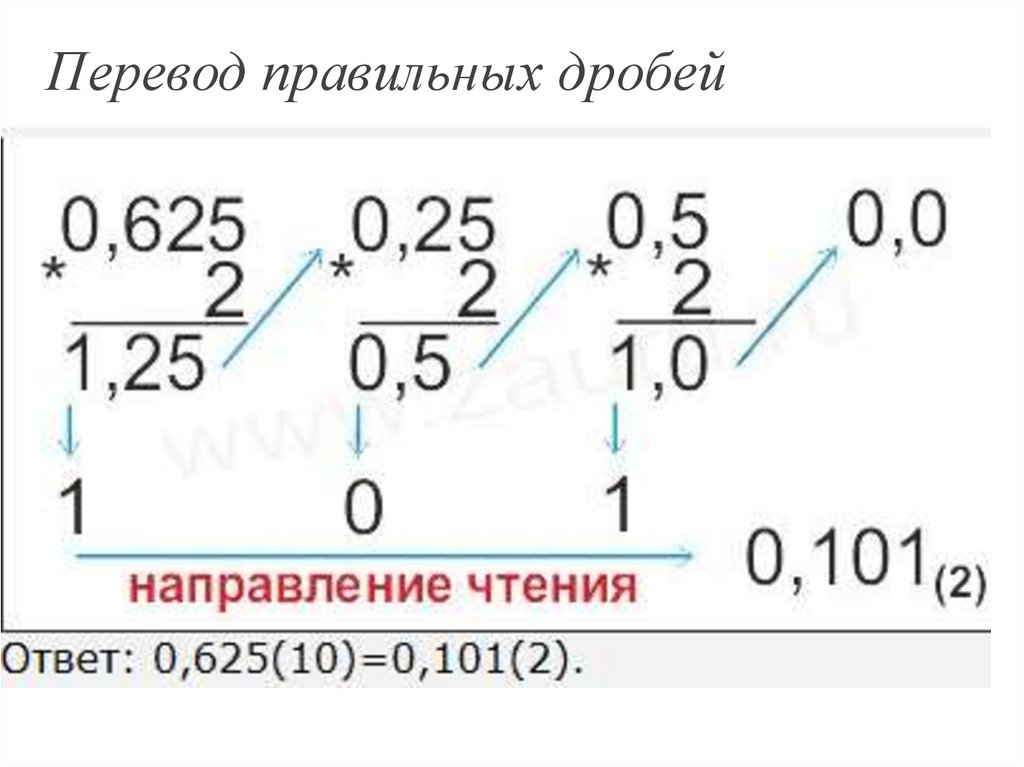
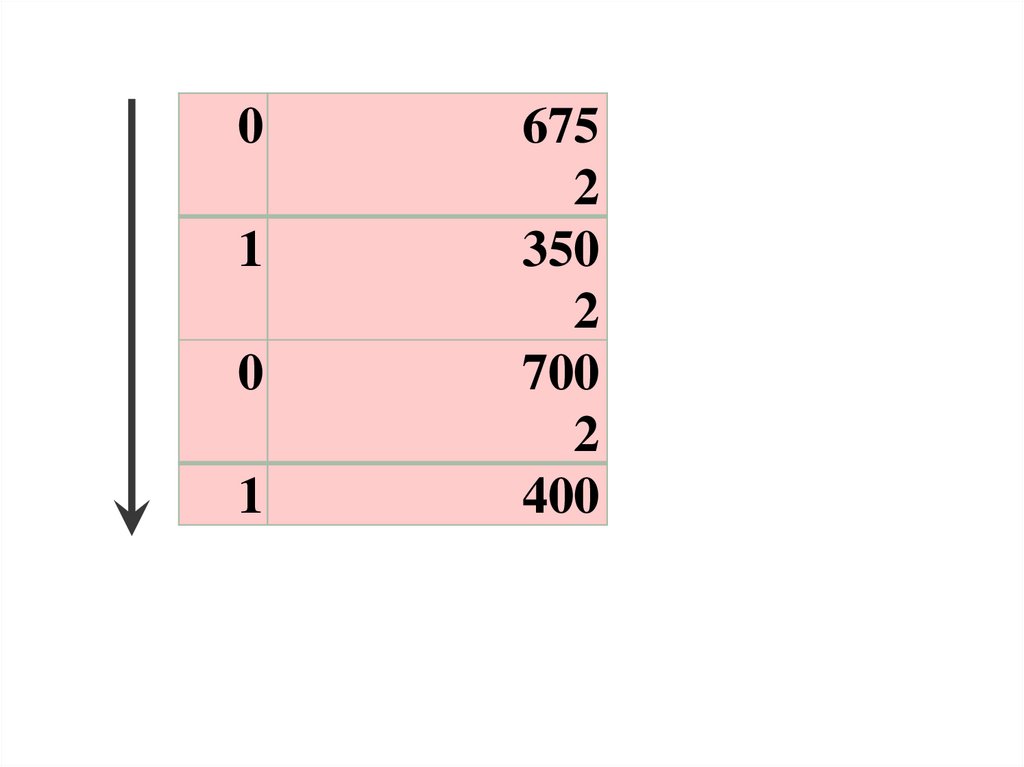
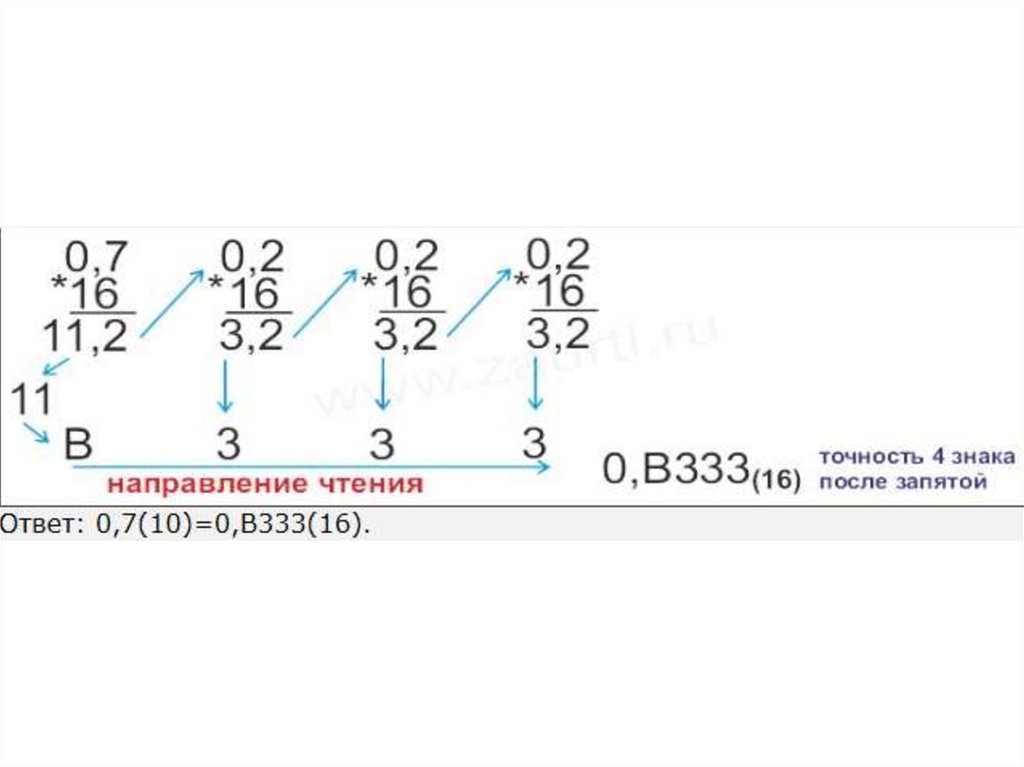
Перевод правильных дробей39.
01
0
1
675
2
350
2
700
2
400
40.
41.
42.
Перевод неправильных дробейА = 19,67510 = 10011,1012
43.
Перевод из недесятичной системыв десятичную
A a q
q
n 1
n 1
0
1
... a0 q a 1 q ... am q
m
n 1
a q
k m
k
k
44.
//из двоичного в десятичноеint var, result = 0;
cout << "Vvedite dvoichnoye chislo: ";
cin >> var;
for (int r = 1; var > 0; r *= 2) {
result += (var % 10) * r;
var /= 10;
}
cout << "Desyatichniy ekvivalent raven: " <<
result << endl;
45.
46.
ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ ВЭВМ
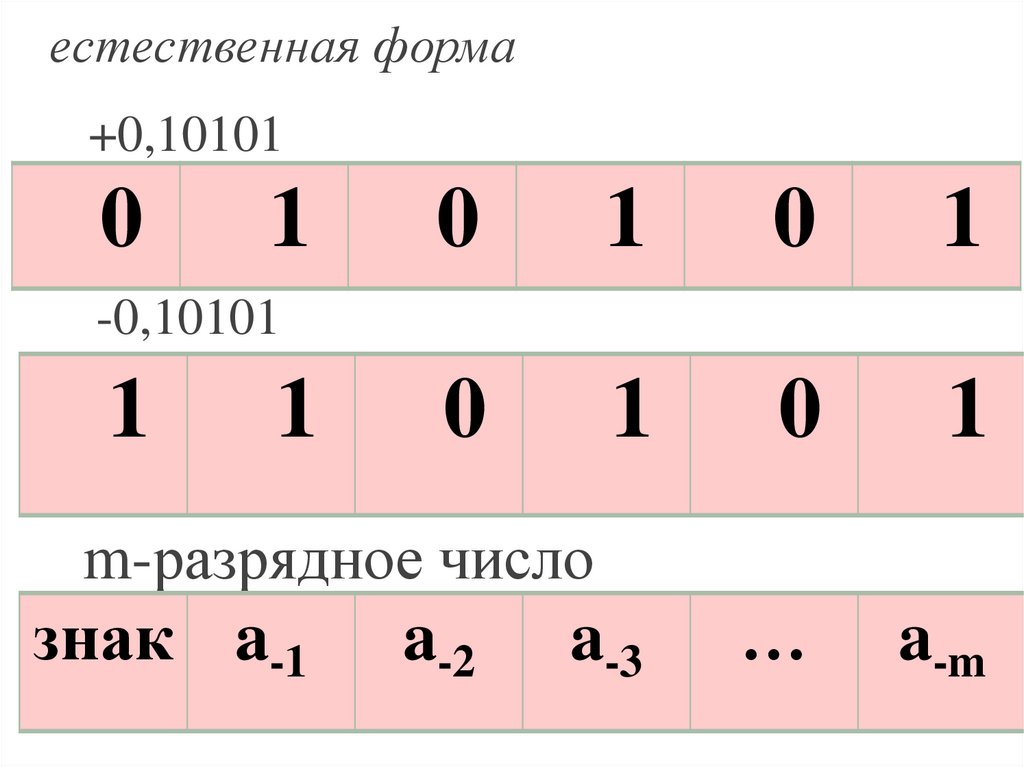
естественная форма (с фиксированным
положением точки)
нормальная форма ( с плавающей
точкой).
47.
естественная форма+0,10101
0
1
0
1
0
1
0
1
0
1
a-3
…
a-m
-0,10101
1
1
m-разрядное число
знак a-1
a-2
48.
A min 2m
0,00...12,
.
А max 1 2
2
m
m
0,11...12.
A 1 2
m
49.
нормальная формаAq M A q ,
L
где МА – мантисса числа А;
q – основание системы счисления;
L – порядок числа А.
17510 = 0,175*103 = 0,0175*104 = 1750*10-1
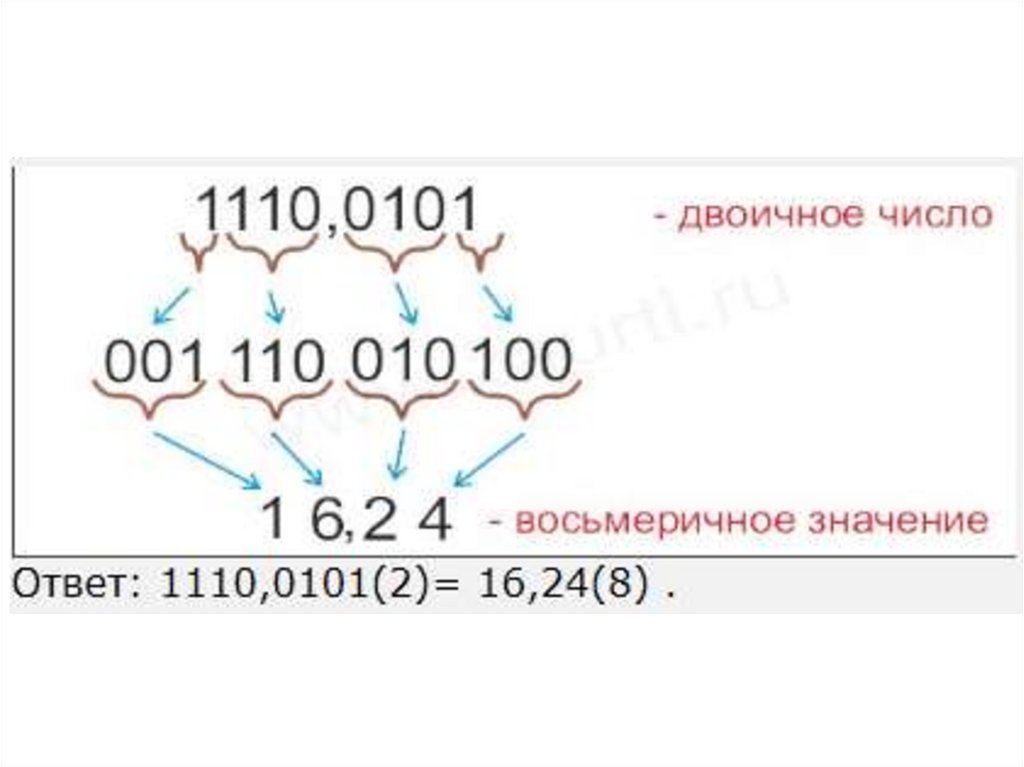
10,1012 = 0,10101*1010 = 101,01*10-01 =
10101*10-11
50.
1q M 1.
± 1
2
2 … k-1 k ± 1
2
p
A 2
2 … p-1 p
( 2 1)
p
.
51.
СПОСОБЫ КОДИРОВАНИЯДВОИЧНЫХ ЧИСЕЛ В ЭВМ
кодирование знака числа;
упрощение операции сложения
отрицательных чисел
52.
специальные машинные коды:прямой;
дополнительный;
обратный.
53.
Прямой кодАпр =
А , если А 0,
1-А , если А < 0.
А = -0,101 → Апр = 1 – (-0,101) = 1.101
Например:
А = 0,10110 Ап= 0.10110
А = - 0,01101 Ап= 1. 01101
54.
Обратный кодAобр =
А, если А 0
-n
102 – 10 +А, если А < 0
n – количество разрядов дробной части числа;
10-n – единица младшего разряда числа А
А = +0,1011 → Аобр = 0.1011
А = -0,1011 → Аобр = 10 – 0,0001 + (– 0,1011)
= 1.0100
Апр = 1.0011 → Аобр = 1.1100
55.
Дополнительный кодАдоп =
А, если А 0 ,
102+А, если А 0
А = +0,1101 → Адоп = 0.1101
А = -0,1101 → Адоп = 10 + (-0,1101) = 1.0011
Адоп = 1.1011 → Апр = 1.0101
56.
Сложение чисел в дополнительном иобратном кодах
















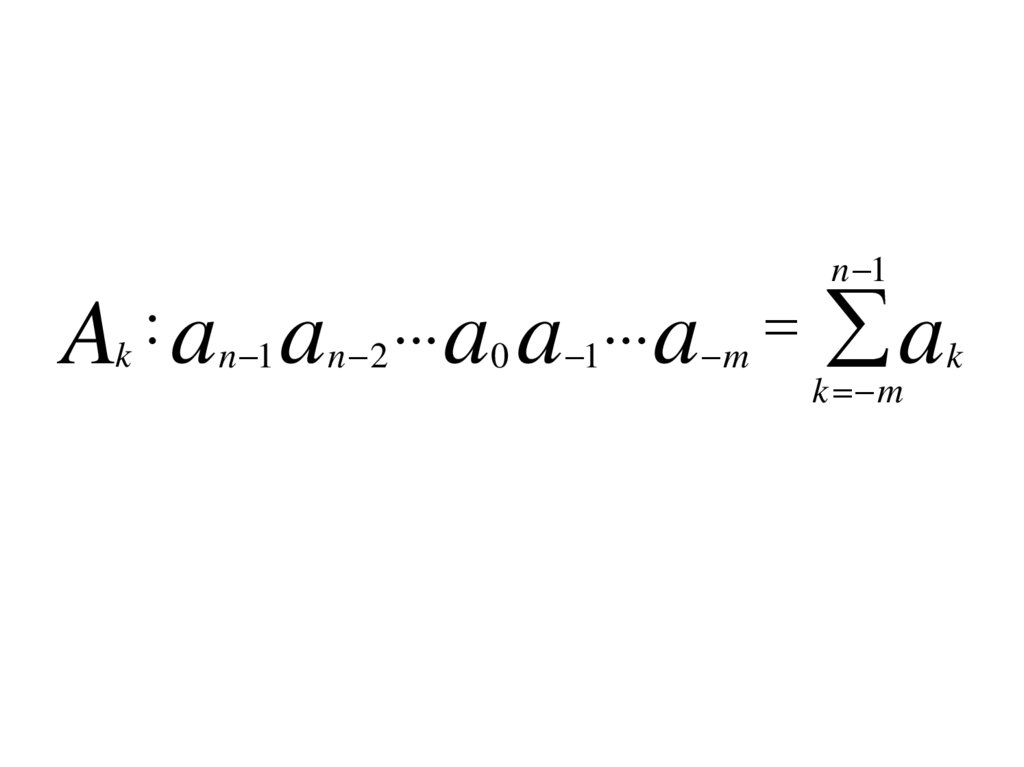
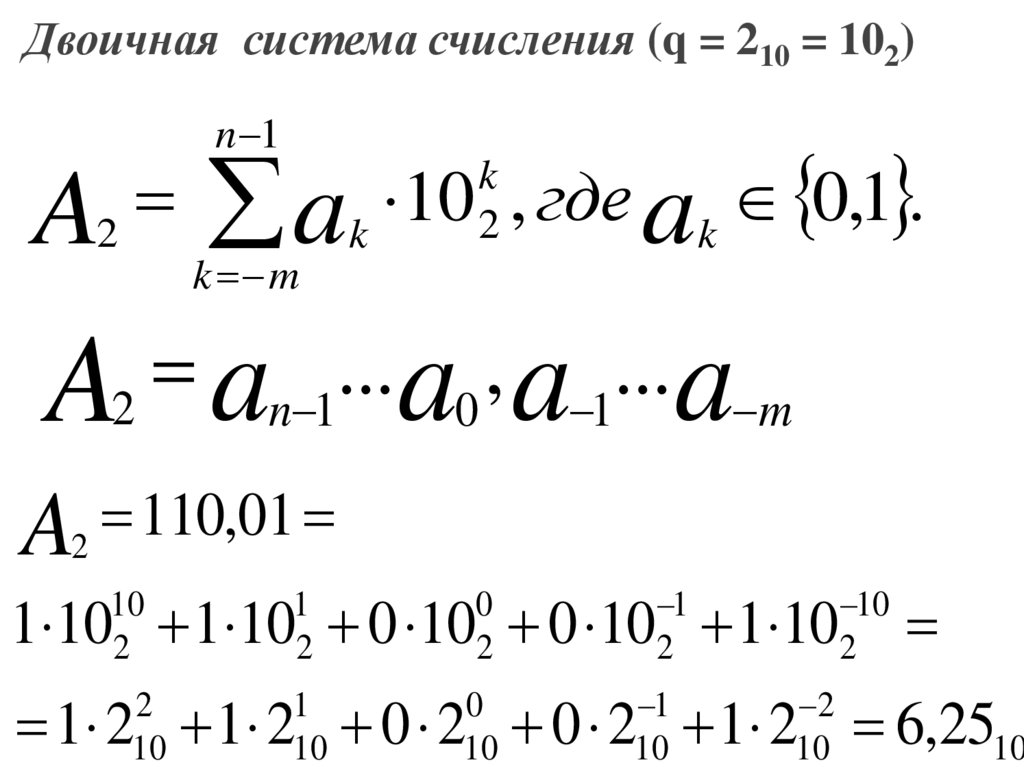

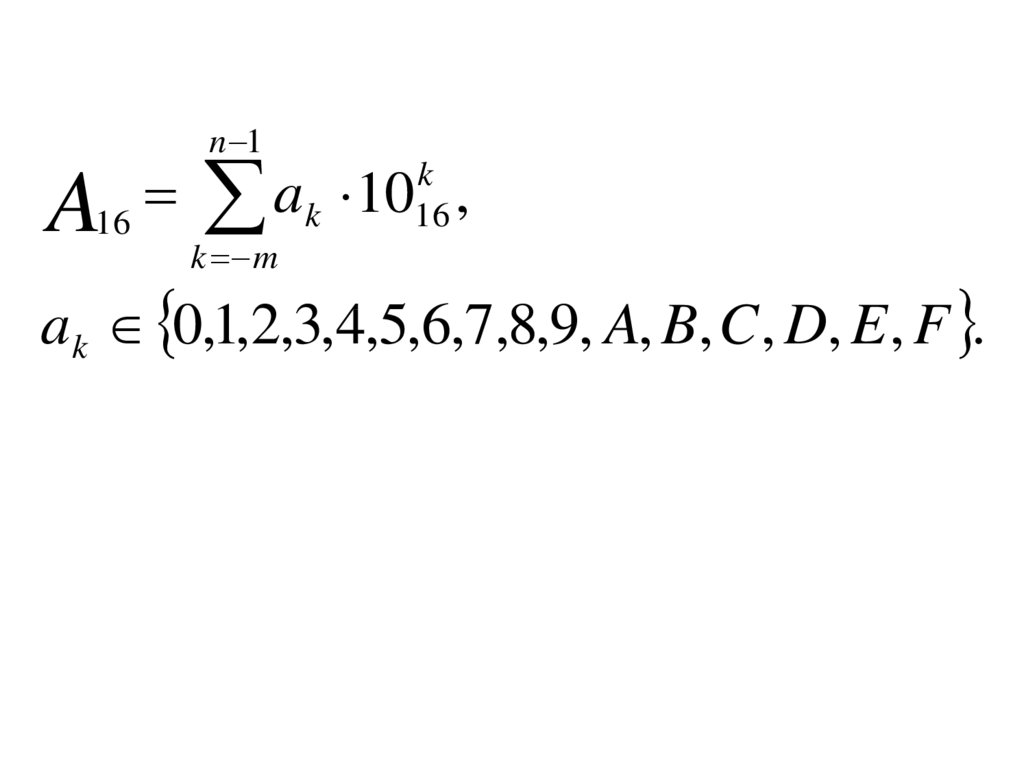













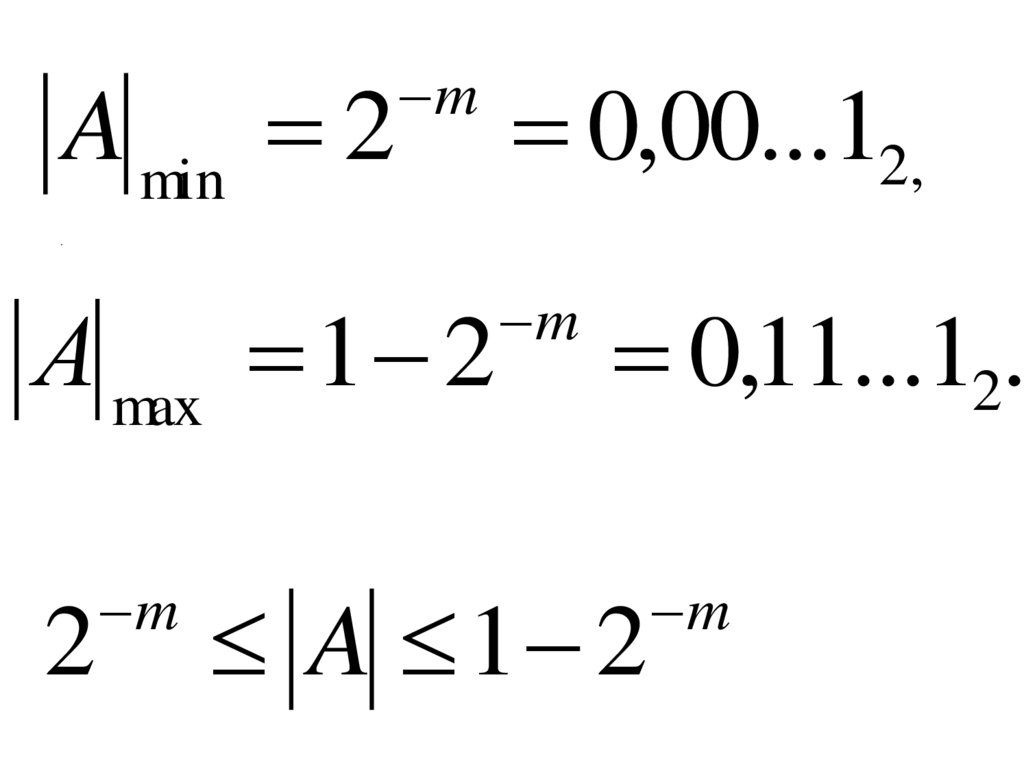

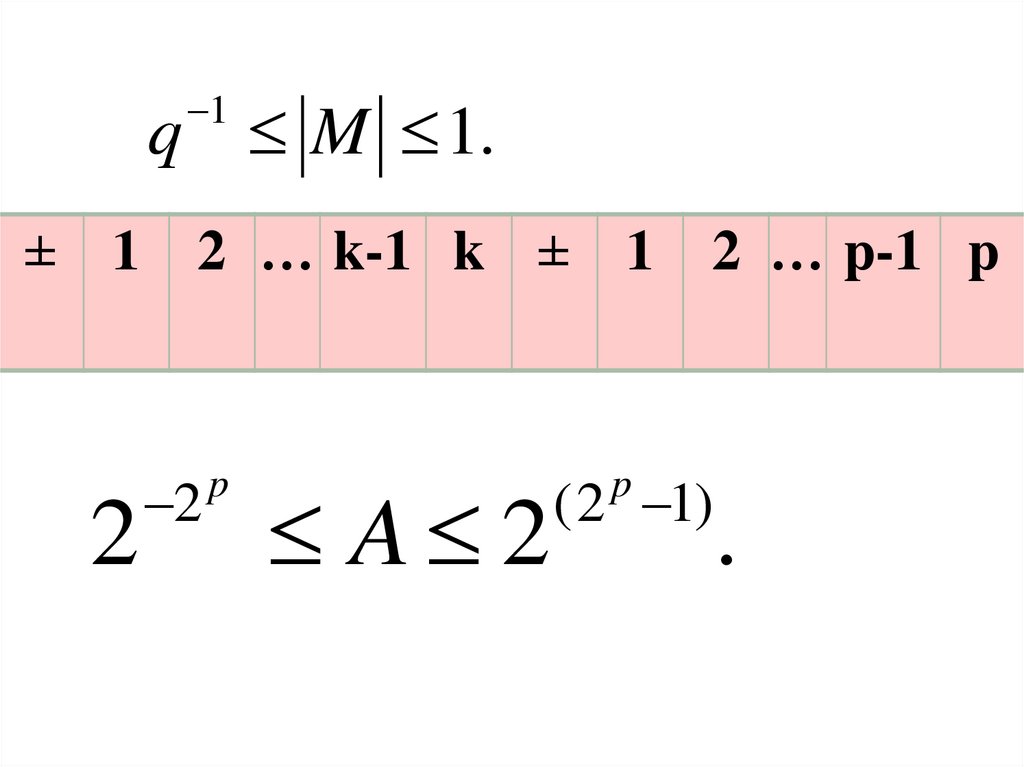


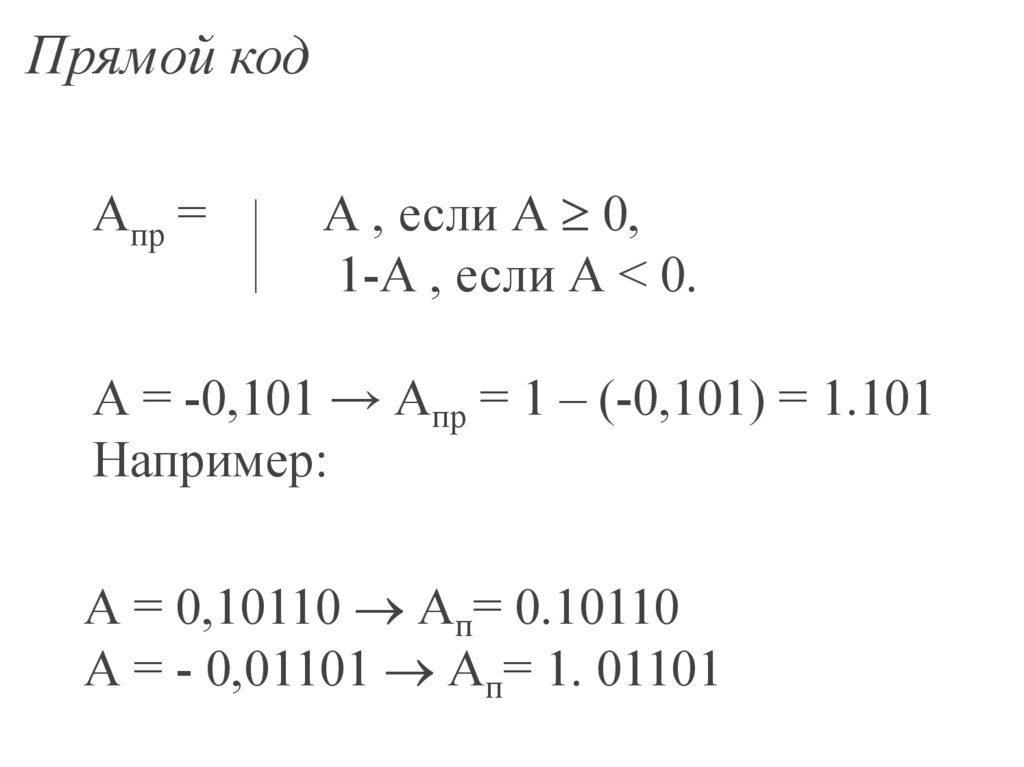

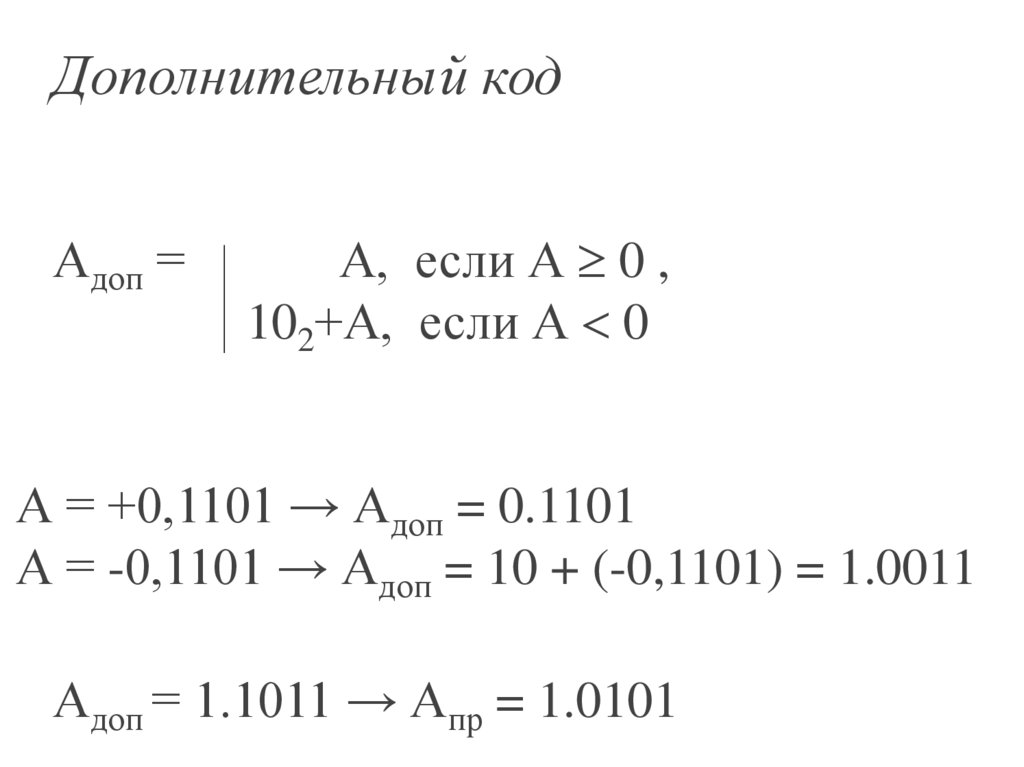


 informatics
informatics








