Классификация моделей и моделирования

1. Классификация моделей

2. 1.2. Классификация моделей и моделирования

Каждая модель создается для конкретной цели и,
следовательно,
уникальна.
Однако
наличие
общих черт позволяет сгруппировать все их
многообразие в отдельные классы, что облегчает
их
разработку
и
изучение.
В
теории
рассматривается
много
признаков
классификации, и их количество не установилось.
Тем
не
менее,
наиболее
актуальны
следующие признаки классификации:
характер моделируемой стороны объекта;
характер процессов, протекающих в объекте;
способ реализации модели.

3.

4. 1.2.1. Классификация моделей и моделирования по признаку "характер моделируемой стороны объекта

1.2.1. Классификация моделей и моделирования по
признаку "характер моделируемой стороны объекта
В
соответствии с этим признаком модели могут
быть:
функциональными (кибернетическими);
структурными;
информационными.
Функциональные модели отображают только
поведение, функцию моделируемого объекта. В
этом случае моделируемый объект
рассматривается как "черный ящик", имеющий
входы и выходы. Физическая сущность объекта,
природа протекающих в нем процессов, структура
объекта остаются вне внимания исследователя,
хотя бы потому, что неизвестны.

5.

При функциональном моделировании
эксперимент состоит в наблюдении за выходом
моделируемого объекта при искусственном или
естественном изменении входных воздействий. По
этим данным и строится модель поведения в виде
некоторой математической функции.
Компьютерная
шахматная
программа
функциональная модель работы человеческого
мозга при игре в шахматы.
Структурное моделирование - это создание и
исследование
модели,
структура
которой
элементы
и
связи)
подобна
структуре
моделируемого объекта. Как мы выяснили ранее,
подобие
устанавливается
не
вообще,
а
относительно цели исследования. Поэтому она
может
быть
описана
на
разных
уровнях
рассмотрения.
Наиболее
общее
описание
структуры - это топологическое описание с
помощью теории графов.

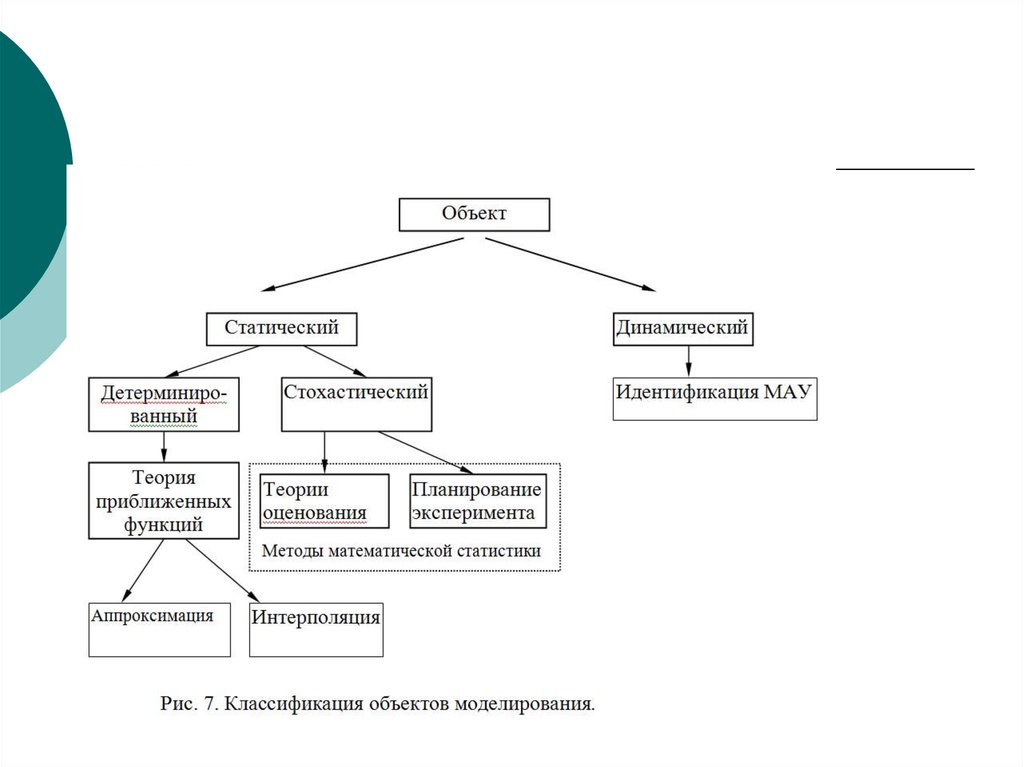
6. 1.2.2. Классификация моделей и моделирования по признаку "характер процессов, протекающих в объекте«

1.2.2. Классификация моделей и
моделирования по признаку "характер
процессов, протекающих в объекте«
Детерминированные
модели
отображают
процессы, в которых отсутствуют случайные
воздействия.
Стохастические
модели
отображают
вероятностные процессы и события.
Статические модели служат для описания
состояния объекта в какой-либо момент времени.
Динамические модели отображают поведение
объекта во времени.
Дискретные модели отображают поведение
систем с дискретными состояниями.
Непрерывные модели представляют системы с
непрерывными процессами.
Дискретно-непрерывные
модели
строятся
тогда, когда исследователя интересуют оба эти
типа процессов.

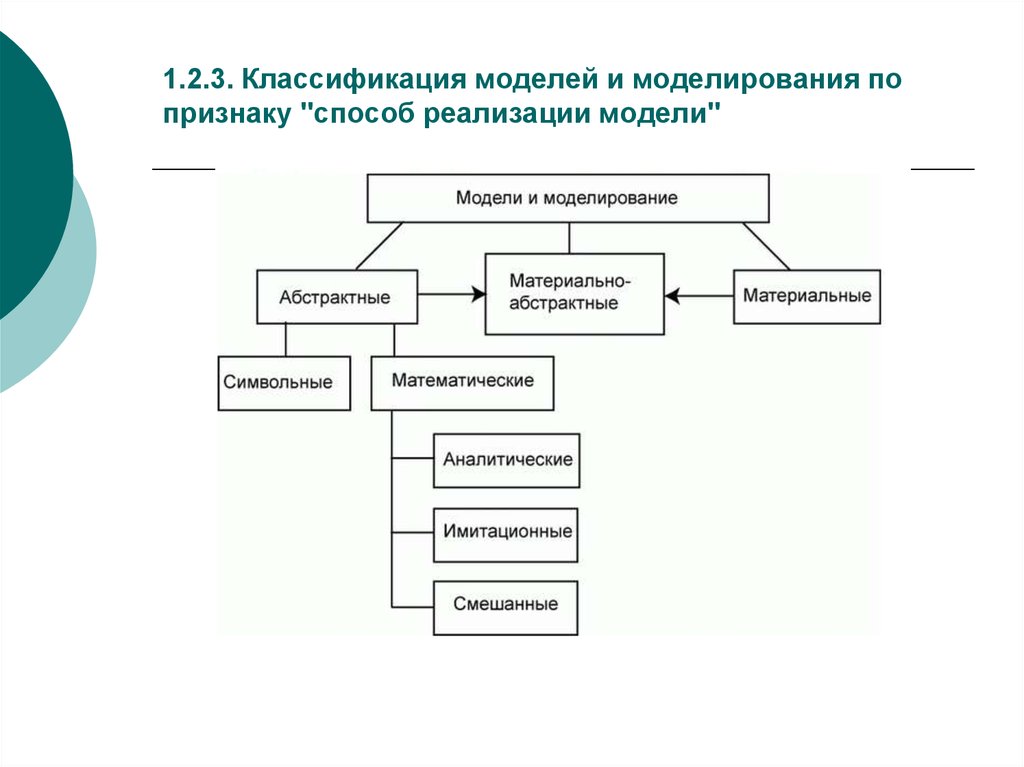
7. 1.2.3. Классификация моделей и моделирования по признаку "способ реализации модели"

1.2.3. Классификация моделей и моделирования по
признаку "способ реализации модели"

8. Основные этапы моделирования

Формулировка целей. В основе всякой
задачи, проблемы моделирования лежит
информация о том, чего собственно добывается,
что хочет субъект от объекта, т.е. каковы его
цели {Z}. Именно эта информация определяет
объект. Существует своеобразный парадокс:
цель определяется объектом, а объект целью.
Этот парадокс разрешается довольно просто.
Субъект, формулируя цель, всегда имеет какието представления об объекте. Эти
представления могут быть очень
приближенными, но всегда отражают некоторые
его свойства, достаточные для эффективной
формулировки целей моделирования. Обычно в
задачах моделирования цель достигается путем
максимизации или минимизации некоторого
критерия, задаваемого в виде целевой
функции.

9.

Изучение объекта.
При этом
требуется понять происходящий процесс,
определить границы объекта с окружающей его
средой, если таковые имеются. Кроме того, на
данном этапе определяются перечень всех
входных и выходных параметров объекта
исследования и их влияние на достижение
целей моделирования.

10.

Описательное моделирование установление и словесная фиксация основных
связей входных и выходных параметров
объекта.
Математическое моделирование - перевод
описательной модели на формальный
математический язык. Цель записывается в
виде функции, которую обычно называют
целевой. Поведение объекта описывается с
помощью соотношений, входные и выходные
параметры объекта на данном этапе в
зависимости от сложности исследуемой
проблемы могут возникать ряд задач чисто
математического характера. Такими задачами
являются задачи математического
программирования, линейной алгебры, задачи
дифференциального и интегрального
исчисления и многие другие.

11.

Выбор (или создание) метода решения
задачи. На данном этапе для возникшей
математической задачи подберется
подходящий метод. При выборе такого метода
необходимо будет обратить внимание на
сложность метода и потребляемые
вычислительные ресурсы. Если подходящего
метода по предъявленным критериям не
окажется, то требуется разработать новый
метод решения задачи. Мы делаем упор на
разработку новых эффективных методов, не
уступающих известным методам по основным
вычислительным характеристикам.

12.

Выбор или написание программы для
решения задачи на ЭВМ. На данном этапе
выбирается подходящая программа,
реализующая выбранный метод решения.
Если такая программа отсутствует, то
необходимо написать такую программу.
Решение задачи на ЭВМ. Вся необходимая
информация для решения задачи вводится в
память ЭВМ вместе с программой. С
использованием подходящей программы
производится обработка целевой информации
и получение результатов решения задач в
удобной форме.

13.

Анализ получаемого решения. Анализ
решения бывают двух видов: формальный
(математический), когда проверяется
соответствие полученного решения
построенной математической модели (в случае
несоответствия проверяется программа,
исходные данные, работа ЭВМ и др.) и
содержательный (экономический,
технологический и т.п.), когда проверяется
соответствие полученного решения тому
объекту, который моделировался. В результате
такого анализа в модель могут быть внесены
изменения или уточнения, после чего весь
рассмотренный процесс повторяется

14.

Модель считается построенной и завершенной,
если она с достаточной точностью характеризует
деятельность объекта по выбранному критерию.
Только после этого модель можно использовать
при расчетах

15. 1.4. Адекватность модели

Адекватность означает, достаточно ли хорошо с
точки зрения целей исследования результаты,
полученные в ходе моделирования, отражают
истинное положение дел.
Термин "адекватность" как видно носит весьма
расплывчатый смысл. Понятно, что
результативность моделирования значительно
возрастет, если при построении модели и
переносе результатов с модели на системуоригинал может воспользоваться некоторой
теорией, уточняющей идею подобия, связанную с
используемой процедурой моделирования

16.

Итак, можно говорить об адекватности модели в
любой ее форме и оригинала, если:
описание поведения, созданное на каком-либо
этапе, достаточно точно совпадает с поведением
моделируемой системы в одинаковых ситуациях;
описание убедительно представительно
относительно свойств системы, которые должны
прогнозироваться с помощью модели.

17.

Предварительно исходный вариант
математической модели подвергается следующим
проверкам:
все ли существенные параметры включены в
модель;
нет ли в модели несущественных параметров;
правильно ли отражены функциональные связи
между параметрами;
правильно ли определены ограничения на
значения параметров;
не дает ли модель абсурдные ответы, если ее
параметры принимают предельные значения.

18.

Окончательное суждение об адекватности модели
может дать лишь практика, то есть сравнение
модели с оригиналом на основе экспериментов с
объектом и моделью. Модель
и объект подвергаются одинаковым воздействиям
и сравниваются их реакции. Если реакции
одинаковы (в пределах допустимой точности), то
делается вывод, что модель адекватна оригиналу.

19. 1.5. Требования, предъявляемые к моделям

Модель должна быть актуальной. Это значит, что
модель должна быть нацелена на важные для
лиц, принимающих решения, проблемы.
Модель должна быть результативной. Это значит,
что полученные результаты моделирования могут
найти успешное применение. Данное требование
может быть реализовано только в случае
правильной
формулировки
требуемого
результата.
Модель должна быть достоверной. Это значит, что
результаты моделирования не вызовут сомнения.
Данное требование тесно связано с понятием
адекватности, то есть, если модель неадекватна,
то она не может давать достоверных результатов.
Модель должна быть экономичной. Это значит,
что эффект от использования результатов
моделирования превышает расходы ресурсов на
ее создание и исследование.

20.

Эти требования (обычно их называют внешними)
выполнимы при условии обладания моделью
внутренними свойствами.
Модель должна быть:
Существенной, т. е. позволяющей вскрыть
сущность поведения системы, вскрыть
неочевидные, нетривиальные детали.
Мощной, т. е. позволяющей получить широкий
набор существенных сведений.
Простой в изучении и использовании, легко
просчитываемой на компьютере.
Открытой, т. е. позволяющей ее модификацию.

21. Вопросы к лекции