Автомат Мили и автомат Мура

1.

Автомат Мили
Закон функционирования
уравнениями:
автомата
Мили
a (t 1) a (t ), z (t )
w(t ) a (t ), z (t )
t 0, 1, ...
определяется

2.

Состояние автомата Мили в следующий момент времени
зависит от его состояния в предыдущий момент и
пришедшего входного сигнала.
Выходной сигнал автомата в данный момент времени также
зависит от его состояния в данный момент времени и
пришедшего входного сигнала.

3.

Состояние автомата Мили в следующий момент времени
зависит от его состояния в предыдущий момент и
пришедшего входного сигнала.
Выходной сигнал автомата в данный момент времени также
зависит от его состояния в данный момент времени и
пришедшего входного сигнала.
Автомат Мили задаётся двумя таблицами — таблицей
переходов и таблицей выходов.
δ
а1
…
аM
λ
а1
…
аM
z1
δ(a1,z1)
…
δ(aM,z1)
z1
λ(a1,z1)
…
λ(aM,z1)
…
…
…
…
…
…
…
…
zF
δ(a1,zF)
…
δ(aM,zF)
zF
λ(a1,zF)
…
λ(aM,zF)

4.

Автомат Мили S1 с тремя состояниями, двумя входными и
выходными сигналами:
δ
а1
а2
а3
λ
а1
а2
а3
z1
a3
a1
a1
z1
w1
w1
w2
z2
a1
a3
a2
z2
w1
w2
w1
Автомат S1 содержит три состояния A = {a1, a2, a3}, два
входных сигнала Z = {z1, z2} и два выходных сигнала
W = {w1, w2}.
Найдём декартово произведение множеств A и Z:
A Z a1 , z1 , a1 , z2 , a2 , z1 , a2 , z2 , a3 , z1 , a3 , z2
A Z A Z 3 2 6

5.

Декартово произведение множеств A и Z содержит 6
компонент. Таблица переходов также содержит 6 клеток.
Каждой паре (состояние, входной сигнал) в момент времени t
функция переходов ставит в соответствие новое состояние, в
которое перейдёт автомат Мили в следующий момент
времени t + 1. Это соответствует первому уравнению автомата
Мили S1:
a(t 1) a(t ), z(t )
Таким образом, функция переходов определяет новое
состояние автомата в зависимости от его текущего состояния
и пришедшего входного сигнала. Она реализует отображение
A Z A.

6.

Аналогично функция выходов для каждой пары (состояние,
входной сигнал) в момент времени t определяет в этот же
момент времени t выходной сигнал при переходе автомата в
новое состояние.
Это соответствует второму уравнению автомата Мили S1:
w(t ) a(t ), z(t )
Функция выходов реализует отображение
A Z W.

7.

Граф автомата — это ориентированный связный граф,
вершины которого соответствуют состояниям, а дуги –
переходам между ними.
Две вершины графа автомата am и as (исходное состояние и
состояние перехода) соединяются дугой, направленной от am к
as, если в автомате имеется переход от am к as, то есть если
as = (am, zf) при некотором входном сигнале zf.
Входной сигнал zf ставится в начале дуги графа автомата,
выходной сигнал wg = (am, zf) ставится в конце дуги.

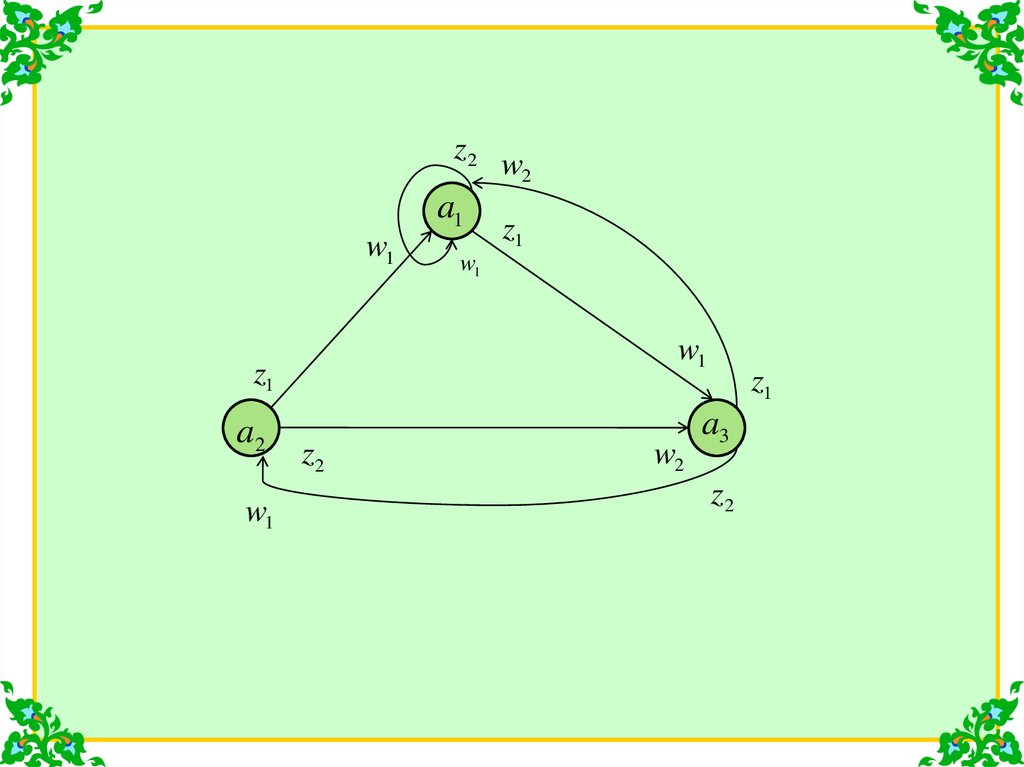
8.

z2
a1
w1
w1
z1
w1
w1
z1
a2
w2
z2
w2
z1
a3
z2

9.

Автомат Мура
Закон функционирования
уравнениями:
автомата
Мура
определяется
a (t 1) a (t ), z (t )
w(t ) a (t )
t 0, 1, ...
Первые уравнения законов функционирования автоматов
Мили и Мура совпадают. Из второго уравнения следует, что
выходной сигнал автомата Мура, в отличие от автомата Мили,
определяется только состоянием автомата.

10.

Т.к. в автомате Мура выходной сигнал зависит только от
состояния, то автомат Мура задаётся одной таблицей—
отмеченной таблицей переходов. В этой таблице в каждом
столбце стоит не только состояние, но и выходной сигнал,
который ему соответствует (он какбы отмечает состояние).
λ(a1)
…
λ(aM)
а1
…
аM
z1
δ(a1,z1)
…
δ(aM,z1)
…
…
…
…
zF
δ(a1,zF)
…
δ(aM,zF)

11.

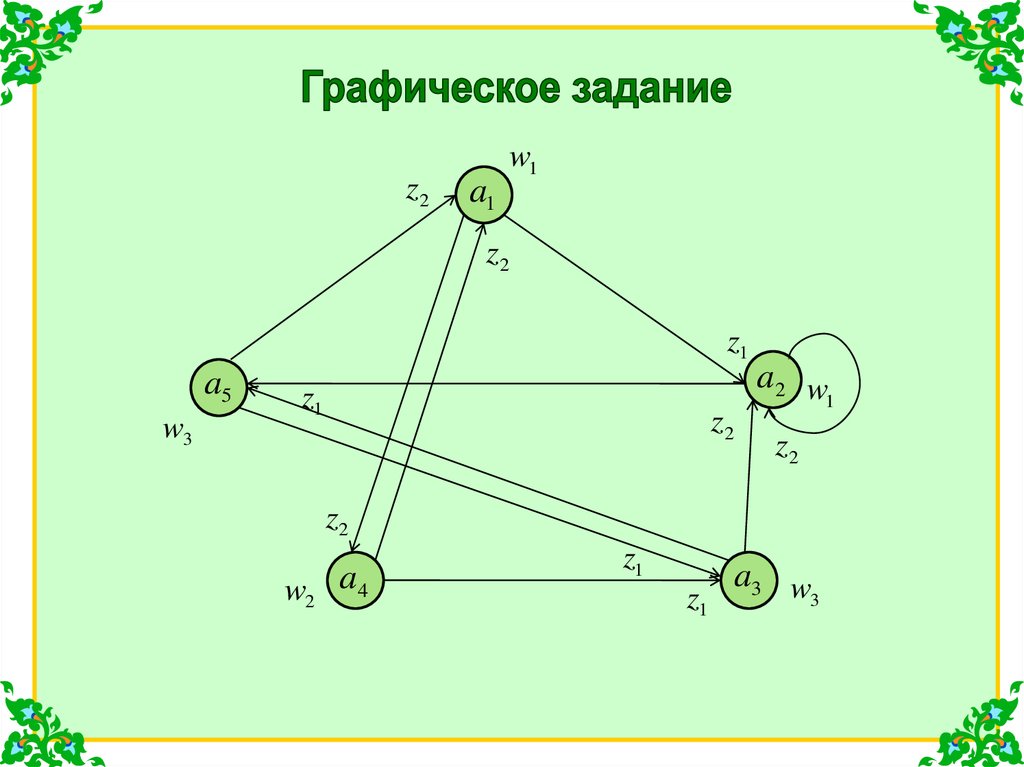
Автомат Мура с пятью состояниями, двумя входными и тремя
выходными сигналами:
w1
w1
w3
w2
w3
а1
а2
а3
а4
а5
z1
а2
а5
а5
а3
а3
z2
а4
а2
а2
а1
а1
A a1 , a2 , a3 , a4 , a5
Z z1 , z2
W w1 , w2 , w3
a1 a1

12.

z2
a1
w1
z2
z1
a5
w3
z1
z2
a2 w
1
z2
z2
w2 a4
z1
z1
a3 w
3

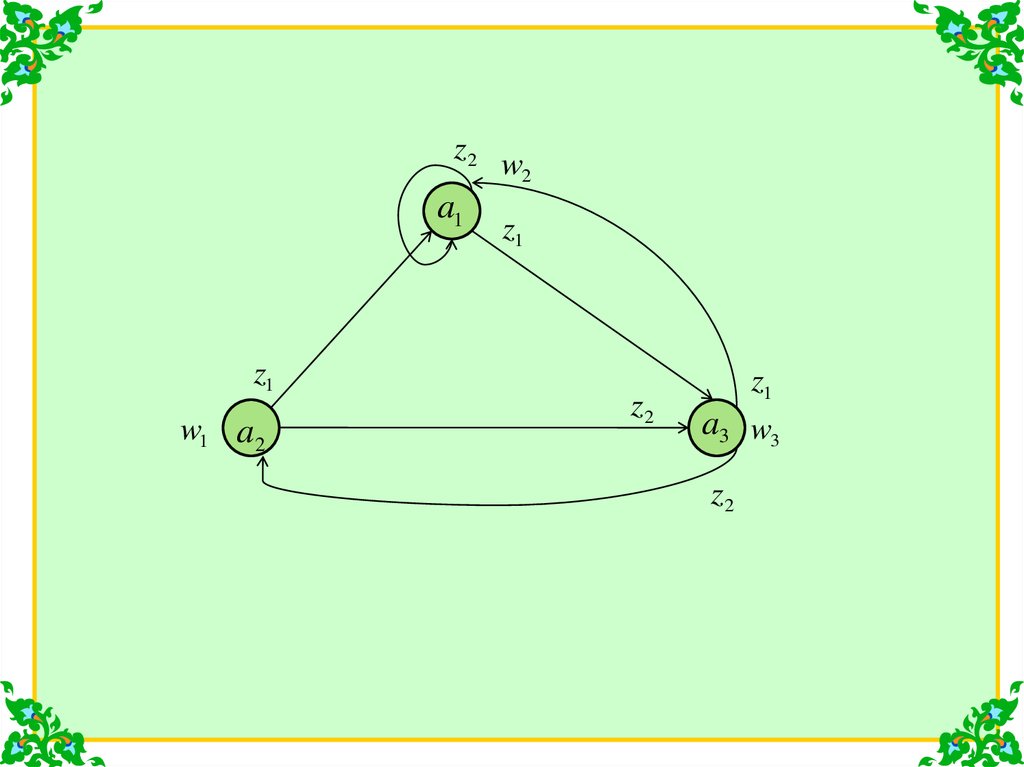
13.

Автомат Мура S2 с тремя состояниями, двумя входными и
тремя выходными сигналами:
A a1 , a2 , a3
w2
w1
w3
а1
а2
а3
z1
а3
а1
а1
z2
а1
а3
а2
Z z1 , z2
W w1 , w2 , w3
a1 a1

14.

z2
a1
z1
w1 a2
w2
z1
z2
z1
a3 w3
z2